Tuesday Sep. 5, 2006
A copy of the Practice Quiz Study Guide
was handed out in class. Still no word on the location of the
Tuesday and Wednesday afternoon reviews. You'll find the
locations posted on the class web page as soon as they are known.
The link to the Sample 1S1P Report
is now working correctly. The Assignment #1 1S1P reports are due
next Tuesday, Sep. 12.
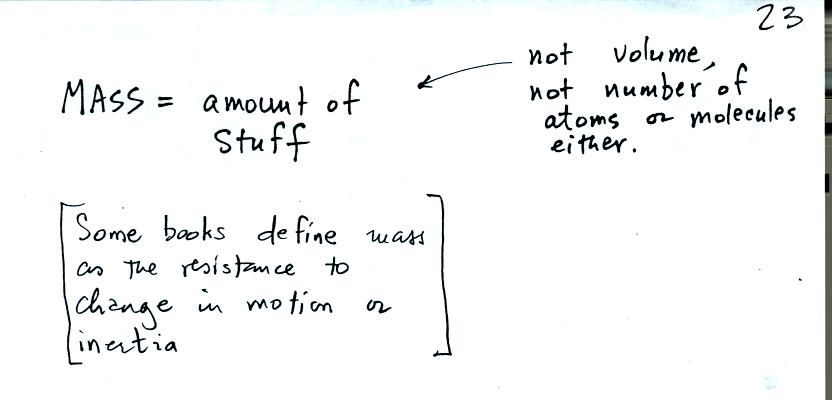
Mass is just a measure of how much of a particular material you
have. It is really not the same as volume, two objects
(different materials) could have the same volume but different
masses. Similarly two objects (different materials) could have
the same total number of atoms or molecules and still have different
masses. The picture below attempts to make clearer the meaning
of inertia or resistance to change in motion which are sometimes used
to define mass.
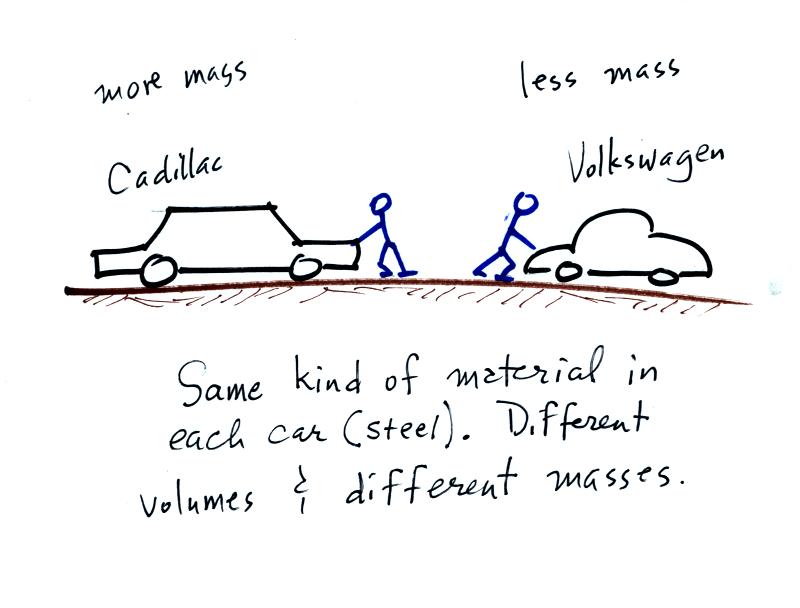
A Cadillac and a volkswagen
have both stalled in an intersection. Both cars are made of
steel. The Cadillac is larger and has more steel, more stuff,
more mass. The Cadillac is also much harder to get moving, it has
a larger inertia (it would also be harder to slow down if it were
already moving).

We generally don't distinquish between weight and mass. This is
because the strength of the gravitational force exerted on a mass and
produces its weight is always the same on the surface of the earth.
A mass of 1 kg will always have a weight of 2.2 pounds
(lbs). Similarly an object that has a weight of 2.2 pounds will,
no matter what its size or composition, have a mass of 1 kg.
You would need to be more careful if you compared objects on the earth
and the moon. This is because the gravitational attractive forces
on the earth and moon are different.

An object with a mass of 1 kg on the earth does not contain the
same amount of stuff as an object that weighs 2.2 pounds on the moon
(the object on the moon would need to have a mass of a little over 6 kg
in order to weigh 2.2 pounds because of the weaker lunar gravity)

Now just to add to the confusion (we
didn't spend much time on this figure in class). The
course instructor weighs around 160 pounds (actually a little less at
the end of the summer bicycling season). Pounds are units of
weight in the English units system. The instructor has a mass of
73 kilograms (kilograms are metric system units for mass).
To determine the instructor's weight in metric units you would need to
multiply the mass by g, the acceleration of gravity on the earth (9.8
m/sec2). You would obtain 715 Newtons (metric units of
force or
weight).
To determine the instructor's mass in English units you would need to
divide the weight by the acceleration of gravity (32 ft/sec2).
You obtain 5 slugs (believe it or not, slugs are English units of mass).
The gravitational acceleration on the moon 5.2 ft/sec2,
about 1/6 of
what it is on the earth. On the moon, the instructor would still
have a mass of 5 slugs but a weight of only 26 pounds.
The sketch on the right edge of the page above gives you an idea of
what g,
the gravitational acceleration, really represents. You drop an
object. After 1 second it will have fallen 16 feet and will be
falling at a speed of 32 ft/sec. At the end of 2 seconds it will
be falling 64 ft/sec, after 3 seconds at 96 ft/sec. The speed of
the falling object is increasing by 32 feet/sec per second. Rate
of change of speed is acceleration. If gravity were the only
force acting on the falling object (and it usually is not) it wouldn't
matter how big or how heavy the object was, it's speed would increase
32 ft/sec per second. A small light weight object and a larger
heavier object would both fall at the same speed and reach the ground
at the same time.
Bottles
containing equal volumes of water and mercury were passed around
class (thanks for being careful with the mercury).
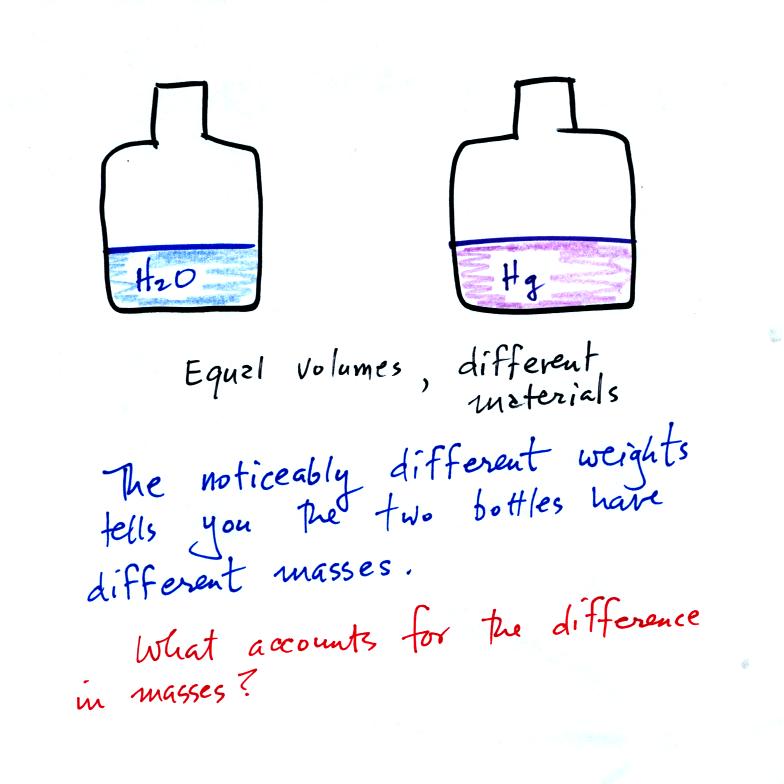
What explains the large difference in masses? Part of the
answer is that the mercury atoms are packed together more tightly than
are the water molecules. A more important difference is that the
water molecules and mercury atoms contain very different numbers of
protoms and neutrons.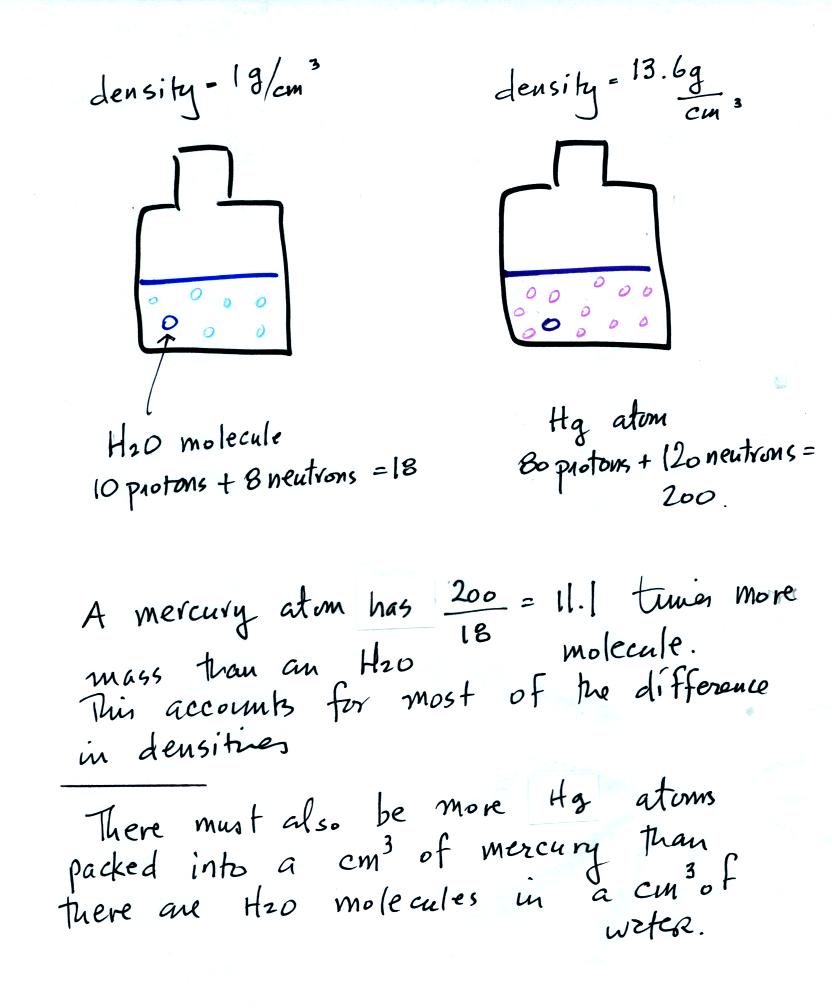

Gravity pulls downward on the air surrounding the earth producing
weight (people didn't really realize that air had mass and weight and
didn't devise ways of measuring air pressure until the
1600s). Air pressure is determined by and tells you something
about the weight of the air overhead. This is one way of trying
to understand atmospheric pressure.
A one inch by one inch column of air extending from sea level to the
top of the atmosphere would, under average conditions, weigh 14.7
pounds (the same as a 4 foot long iron bar that was passed around in
class). Pressure is defined as force divided by area, in this
case weight divided by area. So a typical sea level pressure
would be 14.7 pounds per square inch or psi. These are the same
units used when filling an automobile tire with air. You usually
put about 30 psi into car tires.
We will mostly use millibar (mb) units in our course. Standard
atmospheric
pressure is about 1000 mb or 30 inches of mercury. The second
value refers to the reading from a mercury barometer. 1000
millibars is also equal to 1 bar or 1 atmosphere
.
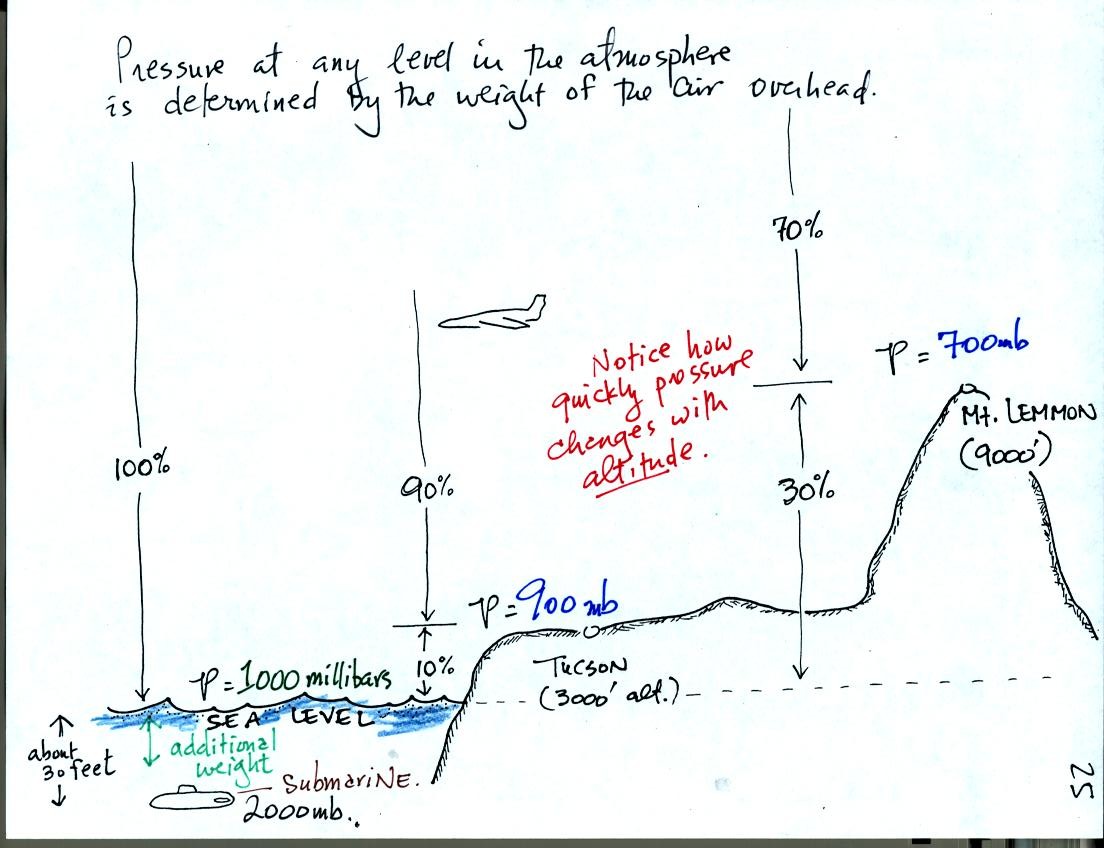
As you move upward through the atmosphere there is less and less air
left overhead. The pressure at any level in the atmosphere is
determined by the weight of the air remaining overhead. Thus pressure
decreases with increasing altitude. Pressure changes much more
quickly when you move in a vertical direction than it does when you
move horizontally. This will be important when we cover surface
weather maps. Meterologists attempt to map out small horizontal
changes or differences in pressure on weather maps. These small
changes are what cause the wind to blow and produce weather.
Pressure increases rapidly as you descend into the ocean. The
pressure at some level in the ocean is determined by the atmospheric
pressure plus the pressure produced by the weight of the water above
you. Water is much denser than air; pressure has doubled to 2000
mb when you are only about 30 feet deep in the ocean.
The following two pages from the
photocopied Class Notes weren't covered in class
Isaac Newton was one of the greatest scientists that ever lived.
Among his accomplishments was the formulation of a law describing the
gravitational attraction between two objects. With a picture or
two and some thought you can understand the roles that the various
variables in the equation play.
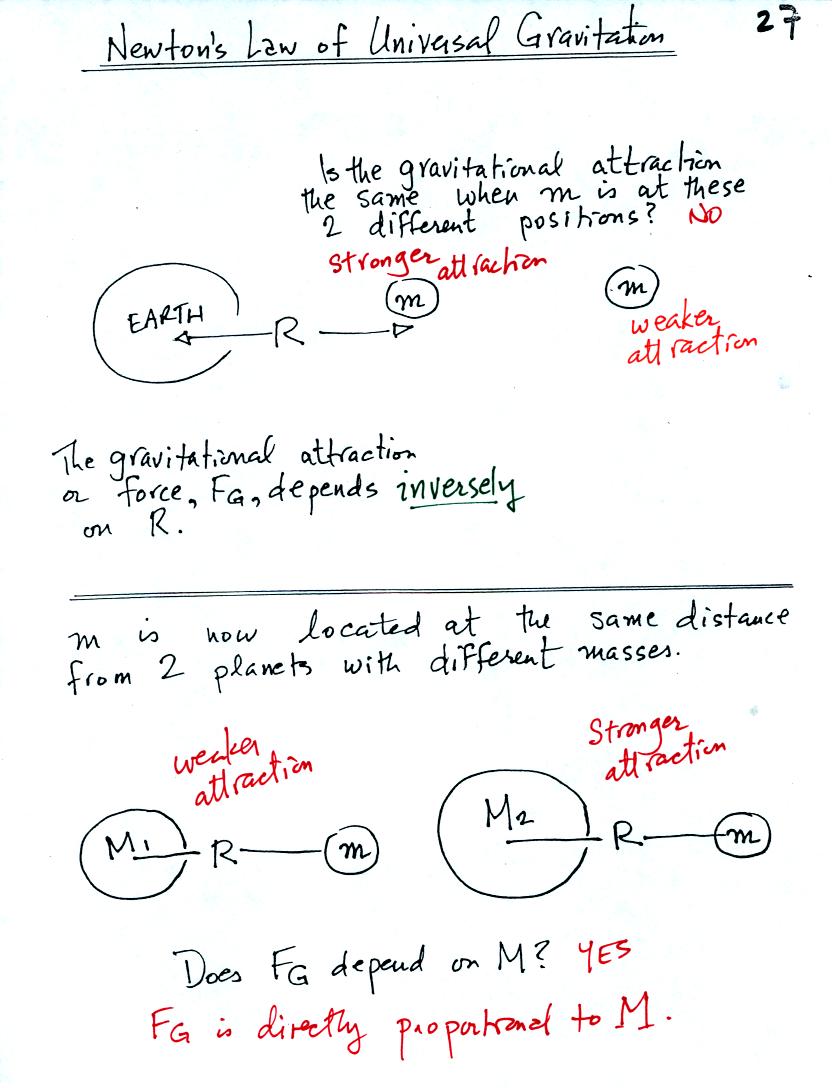
The gravitational attraction between two objects depends first of all
on the distance separating the objects. The gravitational
force becomes weaker the further away the two objects are from each
other (we assume the two objects are spherical). In the bottom
picture above and the top figure below we see that the attractive force
also depends on the masses of the two objects.
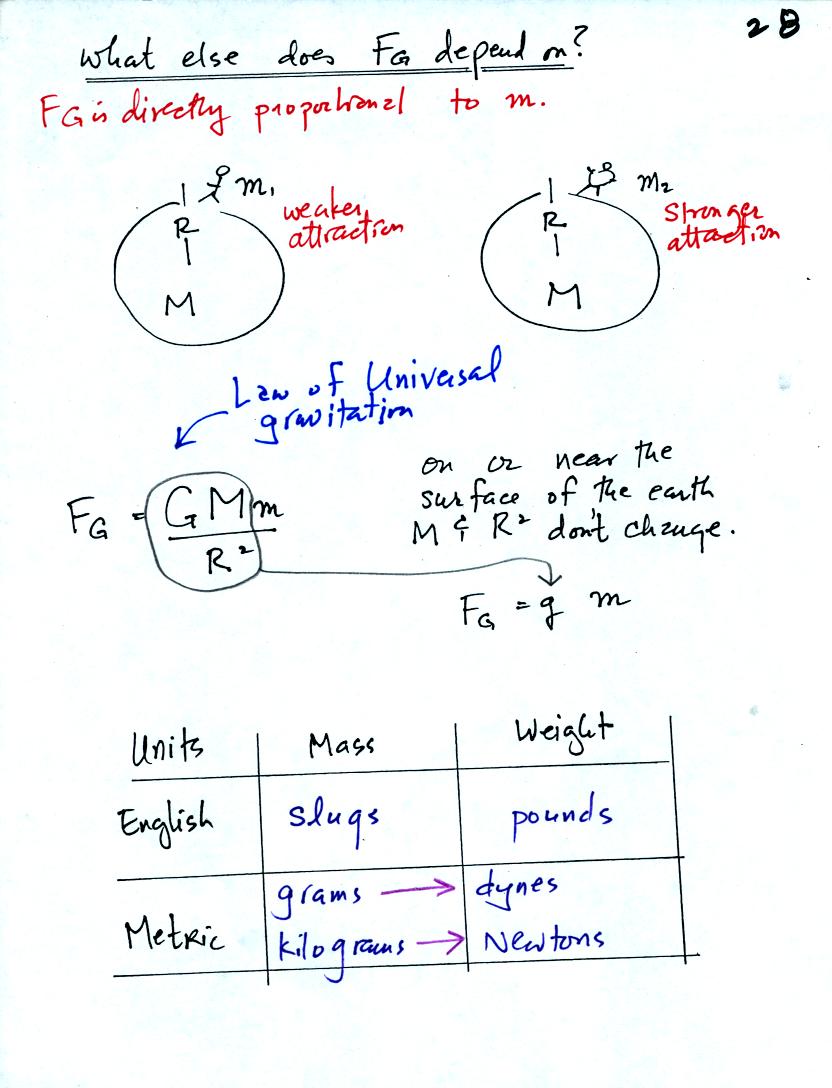
The complete formula is shown in the middle of the page above. G
is a constant. On the surface of the earth G, M, and R don't
change. The gravitational acceleration, g, is just G times Mearth
divided by ( Rearth )2
.
Down at the bottom of the page are the Metric and English units of mass
and weight.
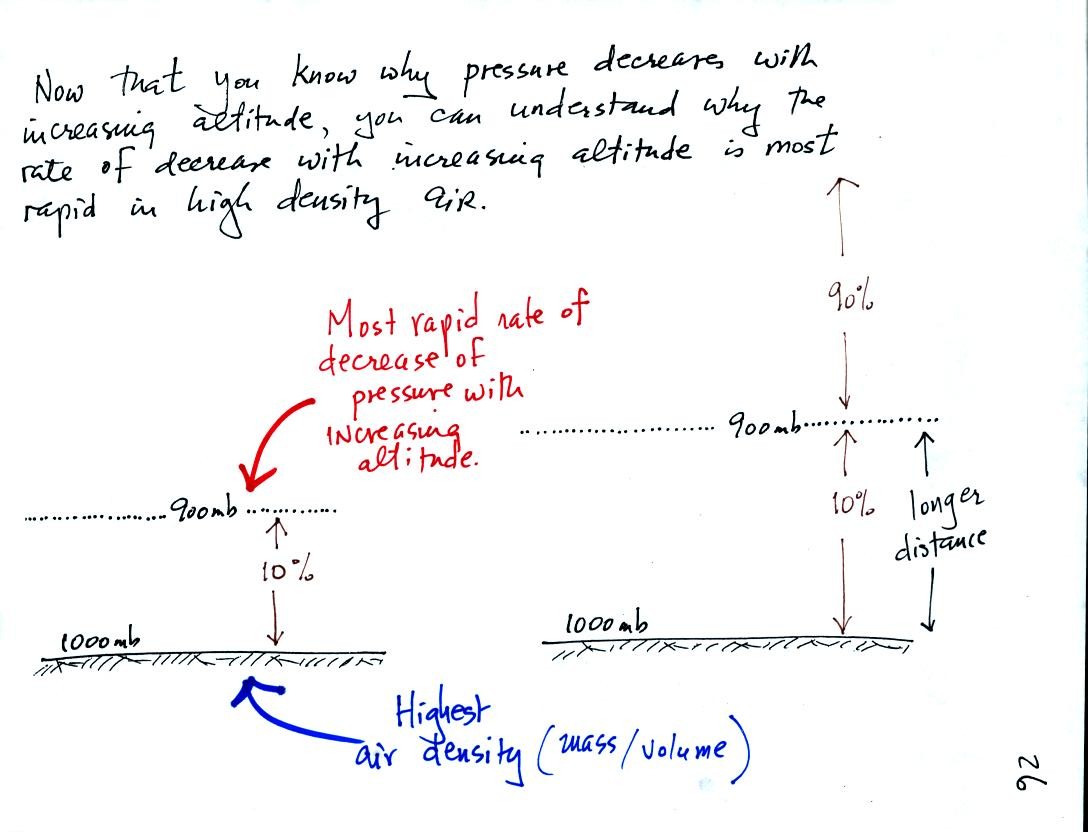
As you move upward from the ground pressure decreases by 100
mb in both
figures. Both layers contain the same amount of air (10% of the
air in the atmosphere). That air is found in a smaller volume in
the figure at left (the layer is thinner). This means the air at
left is denser than the air at right. The drop in air pressure in
the layer at left occurs in a shorter vertical distance than in the air
layer at right. That is a more rapid rate of pressure decrease
with distance than in the layer at right.
The rate of pressure decrease
with altitude is higher in the dense air at left than in the lower
density air at right.
This is a fairly subtle but important concept. We will use it
when we try to understand the intensification of hurricanes later in
the semester.
You'll
find the following material discussed on p. 29 in the photocopied
notes. In 3 simple steps you can understand how a barometer works. It
is probably worth mentioning that barometers are used to measure
pressure (atmospheric pressure). It is not coincidence that the
word bar that appears in barometer
is the same bar that appears in millibars. We will be
learning about weather maps next week and will come across isobars, contours of pressure.
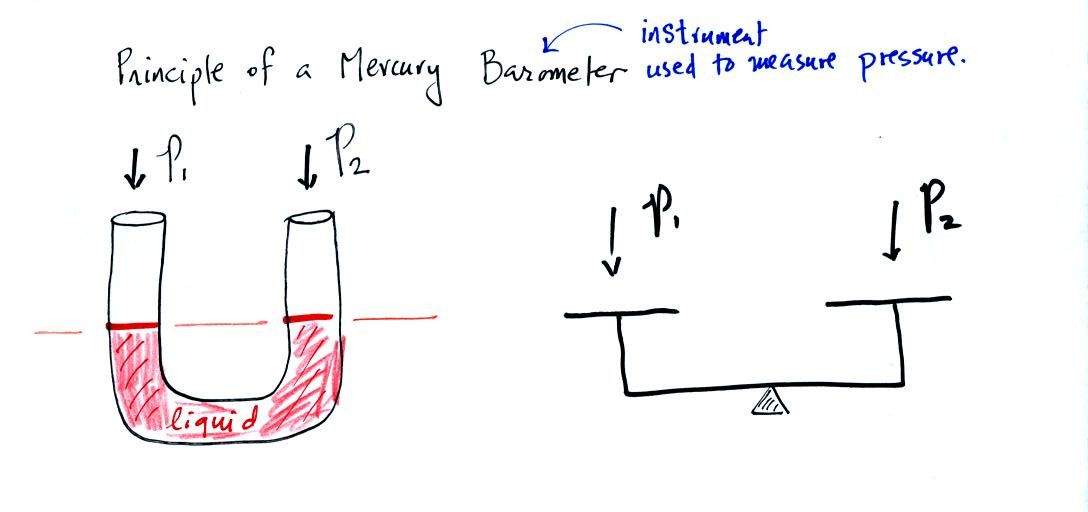
A manometer can be used to measure pressure difference. The
manometer is just a u-shaped tube usually made of glass so that you can
see the liquid that is inside. The liquid can slosh back and
forth just like the pans on a balance can move up and down. A
manometer really behaves just like a pan balance.
In this picture the fact that the liquid levels are the same in the
right and left tubes means P1 and P2 are the same (note you really
don't know what P1 and P2 are, just that they are equal).
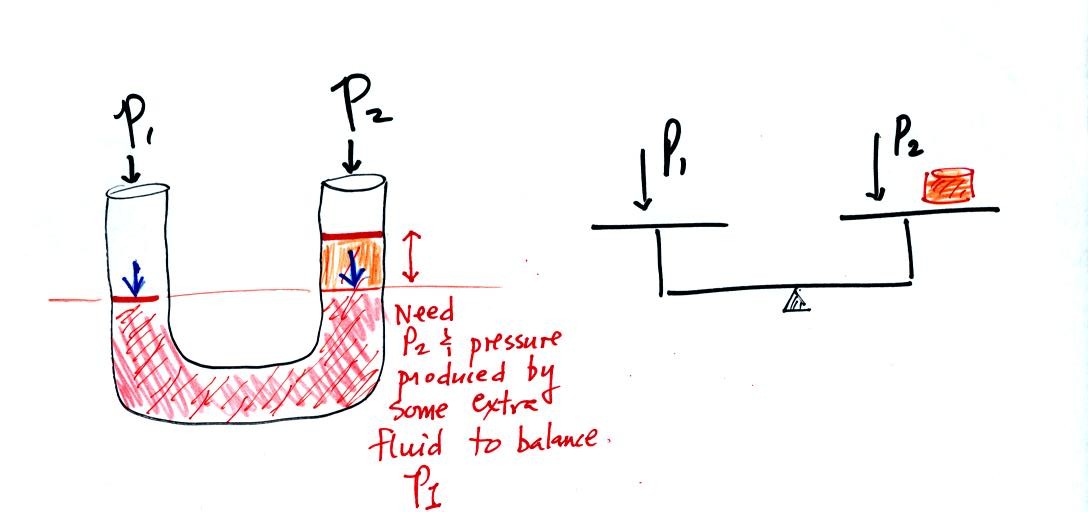
Now the situation is a little different, the liquid levels
are no
longer equal. The orange shaded portion of the liquid is the
balance that we had in the previous picture. The pressures at the
levels of the two blue arrows are equal (the red shaded fluid is the
balance). P2 is not able by itself to balance P1, P2 is lower
than
P1. P1 plus the pressure produced by the column of extra liquid
on the right balances P1. The height of the column of extra
liquid provides a measure of the difference between P1 and P2.
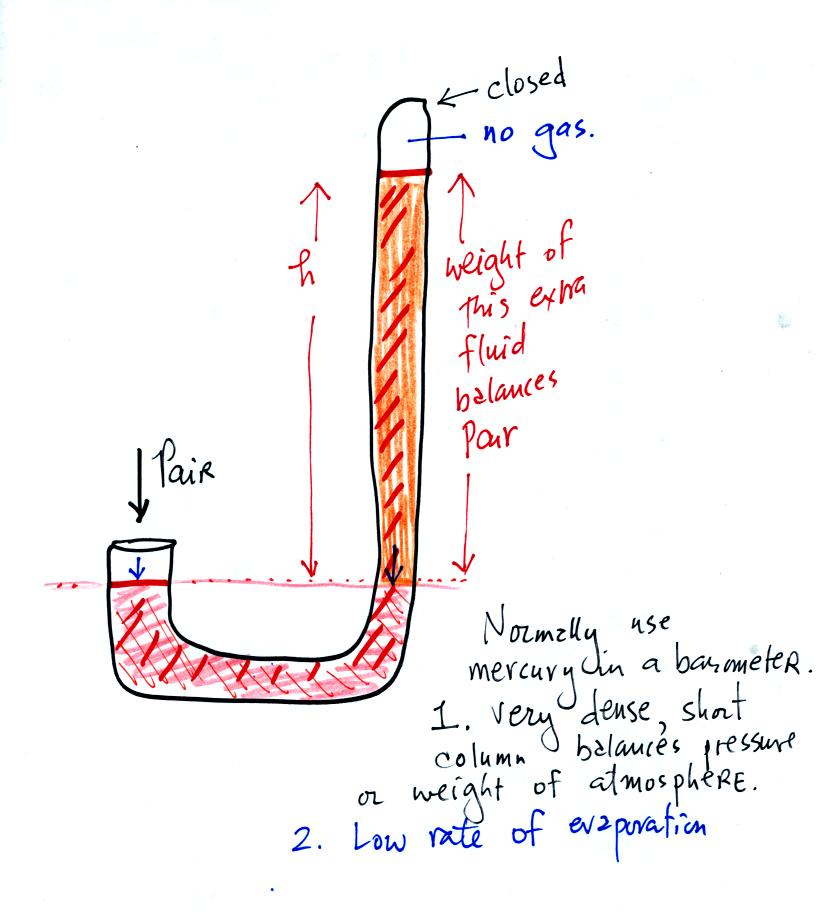
We have changed the manometer by lengthening the right tube
and sealing
it off at the top. Air pressure can't get into the right tube any
more. The balance is again shaded in orange at the bottom of the
barometer. Pressures at the two blue arrows indicated
are equal.
Pair is equal to the pressure produced by the column h inches tall on
the right. If Pair changes, h will change. You now a way of
measuring and monitoring the atmospheric pressure.
Barometers like this are usually filled with mercury. Mercury is
a liquid. You need a liquid that can slosh back and forth in
response to changes in air pressure. Mercury is also dense which
means the barometer won't need to be as tall as if you used something
like water. A water barometer would need to be over 30 feet
tall. With mercury you will need only a 30 inch tall column to
balance the weight of the atmosphere at sea level under normal
conditions (remember the 30 inches of mercury pressure units mentioned
in class a week or so ago). Mercury also has a low rate of
evaporation so you don't have much mercury gas at the top of the right
tube.
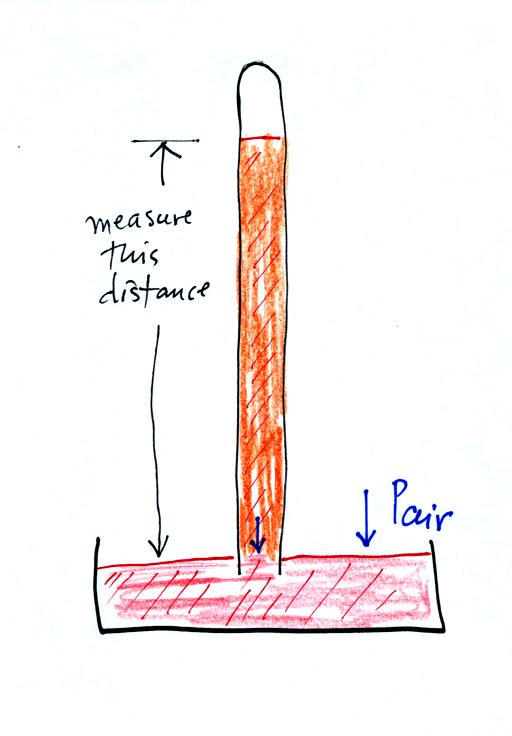
Finally here is a more conventional barometer design. The bowl of
mercury is usually covered in such a way that it can sense changes in
pressure but not evaporate and fill the room with poisonous mercury
vapor.
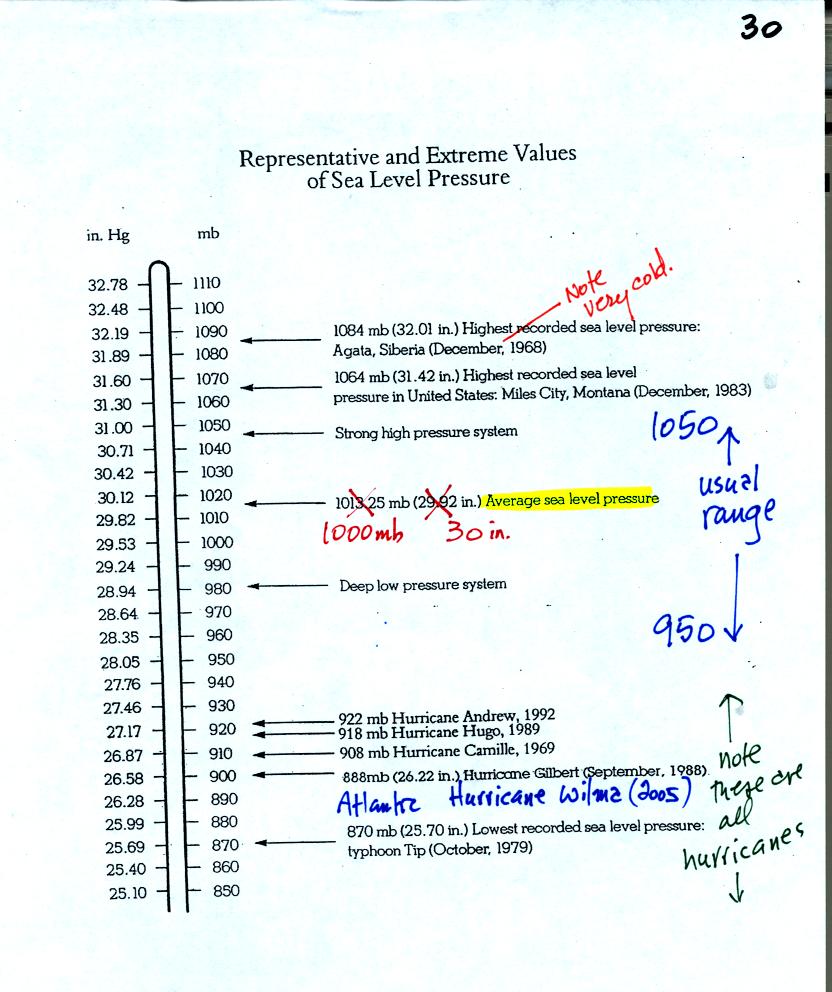
Under normal conditions sea level pressure is about 1000 mb (about 30
inches of mercury). It can be higher and lower than this but
usually falls in the range 950 mb to 1050 mb. Record high and low
sea level pressure values are shown in the chart. Note the record
low values have all be observed in hurricanes.
Hurricane Wilma set a new low sea level pressure reading (882 mb) last
year for the Atlantic. At the time the winds were 185 MPH.

















