Thu., Sep. 28 notes

Thursday Sept. 28, 2006

A new optional assignment was handed out in class today. It is due at the beginning of class next Tuesday. If you would like to complete the assignment and weren't in class on Thursday, you will need to come by PAS 588 to pick up a copy.

We will finish the material on the seasons today. Even though the next quiz is two weeks away, it would be a good idea to make sure you understand this material now rather than waiting until a day or two before the quiz. A Seasons Study Guide is now available to help you in that effort.

Some information about the grading of the 1S1P reports is now available.

We began with a quick review of what we learned last Tuesday about the winter solstice. One of the important things we learned was that there are very small seasonal changes at the equator. This is because the days are always 12 hours long and the sun is always pretty high in the sky at noon (66.5 degrees or higher). This means about the same amount of energy arrives at the ground every day of the year. There really is no summer or winter at the equator.

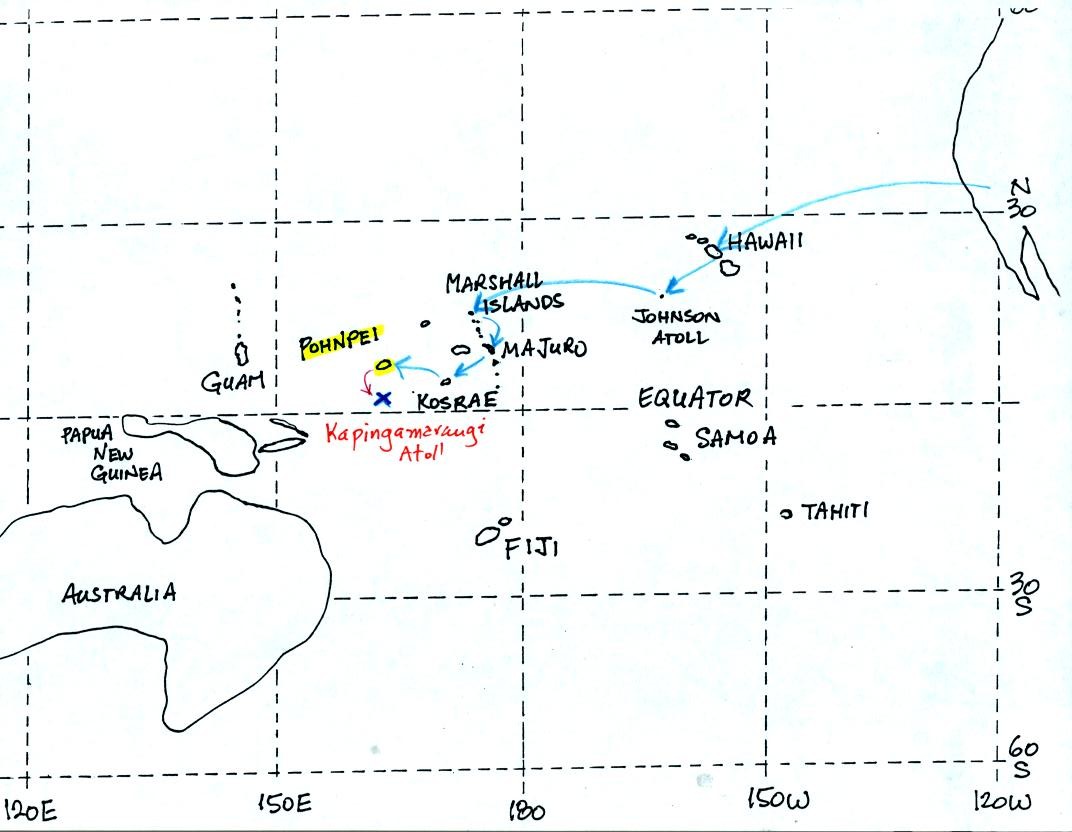
We took a quick look at a place where there is essentially no seasonal change during the year. Pohnpei, in the Federated States of Micronesia is located at 7o N latitude in the middle of the Pacific Ocean. Commercial airlines fly to Pohnpei on the way to and from Guam (you'll find the map below on p. 81 in the photocopied class notes). Your course instructor had the opportunity to visit Pohnpei while enroute to Kapingamarangi Atoll as part of a large meterological field experiment.

The next figure gives a little information about the island of Pohnpei. Pohnpei and some of the nearby islands are popular tourist destinations because of world class snorkeling and scuba diving.

There is a weather station at Kolonia, the largest city on Pohnpei island operated by NOAA (the US National Atmospheric and Oceanic Administration). The next figure shows the monthly average temperatures for the city of Kolonia.

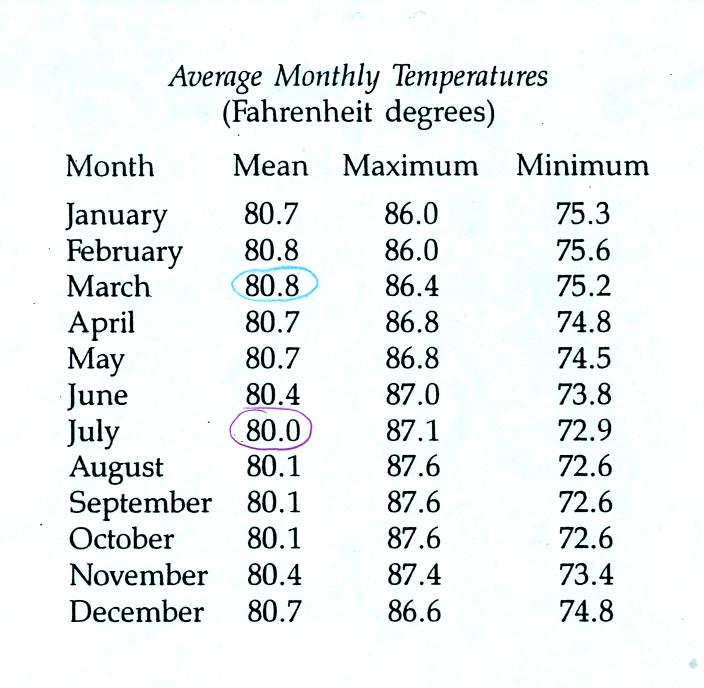
There is less than 1 F difference between the warmest and coldest months in Kolonia. By contrast, in Tucson July has an average temperature of 86 F while January and December have monthly average temperatures of 52 F. There is no winter or summer on Pohnpei. The interior of Pohnpei receives around 400 inches of rain in a year, making it one of the rainiest locations on earth.

Pohnpei has such a small annual range of temperature because of its low latitude and because it is surrounded by ocean.

Next we had a brief look at the summer solstice,

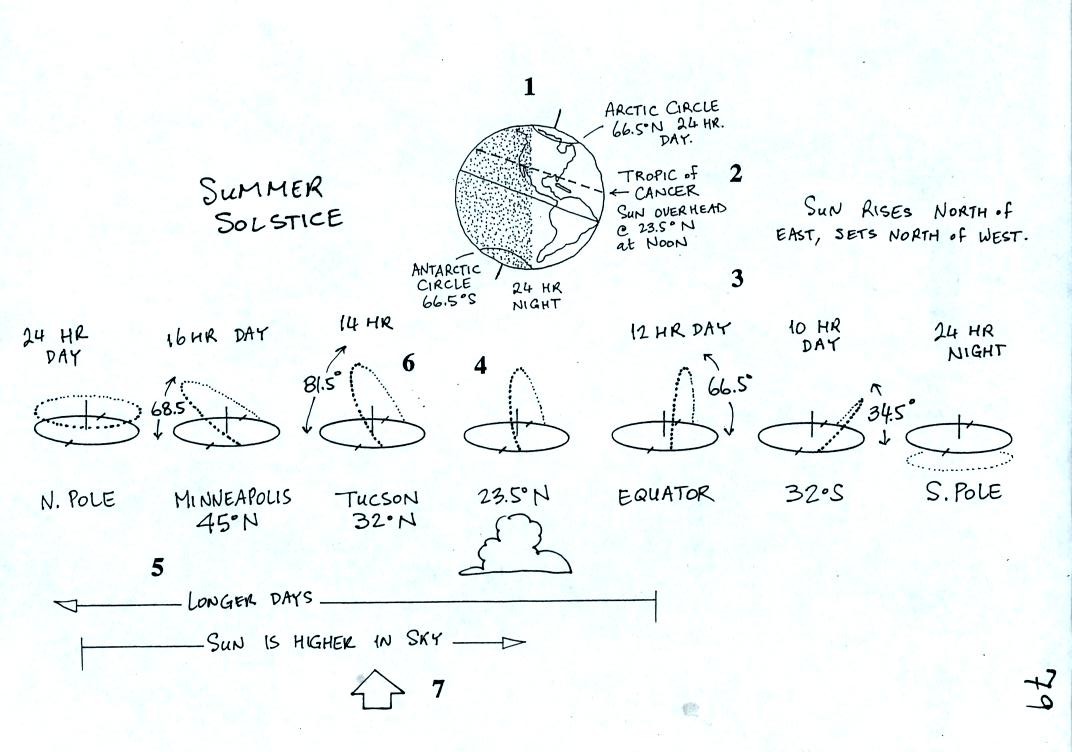
Each of the numbered points is discussed on p. 80 in the photocopied class notes.

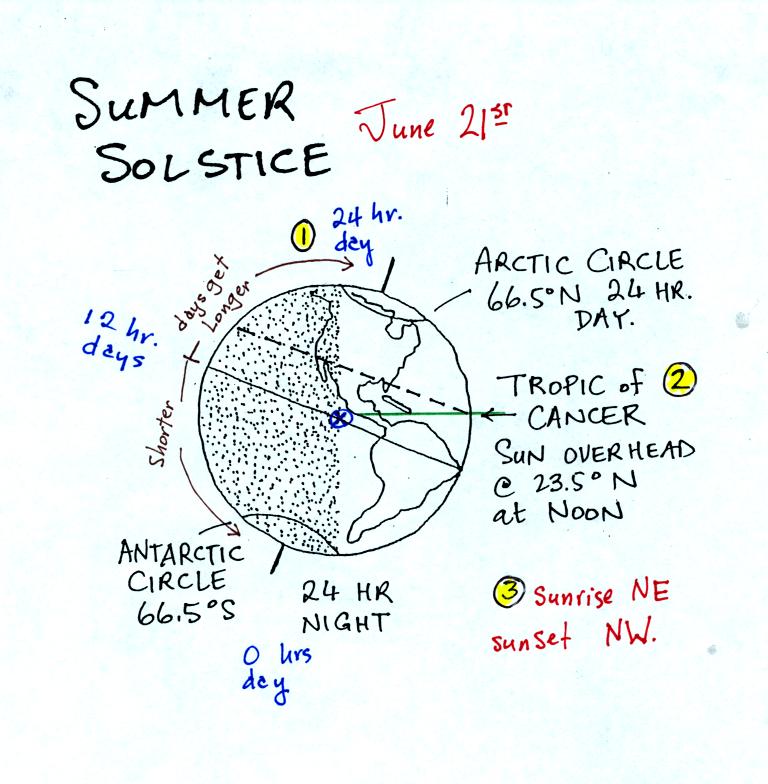
You should be getting pretty good at this by now.

1.     There is 24 hours of daylight above the Arctic Circle on June 21, the summer solstice. South of the Antarctic circle 0 hours of daylight. At the equator, halfway in between, the days are 12 hours long. Days get longer with increasing latitude in the northern hemisphere and get shorter with increasing latitude in the southern hemisphere.

2.     The sun will pass straight overhead at noon at 23.5 north latitude, the Tropic of Cancer.

3.     The sun will rise in the NE and set in the NW on the summer solstice.

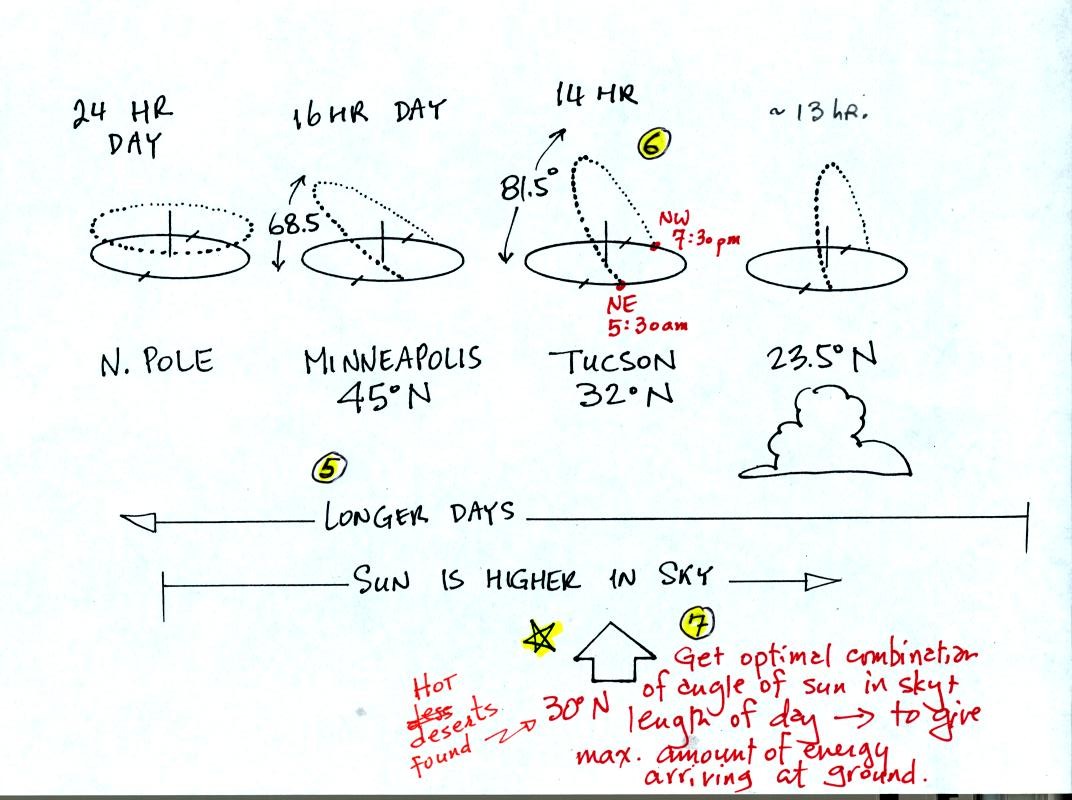
5.     As you move from the equator toward higher latitude in the northern hemisphere the days get longer. The days are 12 hours long at the equator, 14 hours long in Tucson, 16 hours long in Minneapolis and 24 hours long north of the Arctic circle.

6.     In Tucson the sun rises in the NE around 5:30 am or so. It then moves over into the southern sky and is 81.5 degrees above the southern horizon at noon. It is not directly overhead but it is close. The sun sets in the NW around 7:30 pm. The long days and the intense sunlight arriving at the ground when the sun is high in the sky means there will be much more energy making it to the ground this time of the year. The ground gets hotter; this is summer.

7.     Now you might think that Minneapolis would get even more sunlight energy during the day because the days are 16 hours long there. Note however that the sun is lower in the sky at noon. The two factors (length of day, angle of the sun in the sky) that determine how much energy arrives at the ground are working against each other.

That means that somewhere between 23.5 degrees and the north pole there will be an optimum combination of length of day and angle of the sun in the sky. This optimal combination will mean the maximum amount of sunlight energy makes it to the ground. The optimal combination occurs near 30 degrees latitude. THis is where the world's hot deserts are found.

This next figure wasn't shown in class. It was drawn in response to a question after class. The figure shows the path of the sun in Tucson on the summer solstice (sunrises in the NE and sets in the NW), the eqinoxes (sunrise in the E, sunset in the W), and the winter solstice (sunrise in the SE, sunset in the SW).

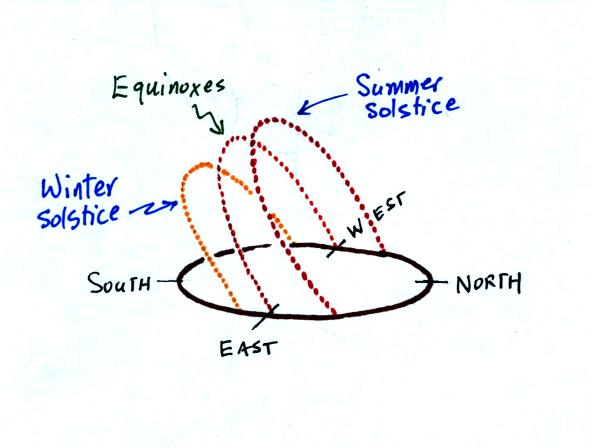
The sun reaches a point 34.5 degrees above the southern horizon on the winter solstice, the sun is 58 degrees above the horizon on the equinoxes, and 81.5 degrees above the horizon on the summer solstice.

Next we quickly went over the following introduction to the material at the beginning of Chapter 2. We do this because it is easy to lose sight of our overall objective because of all the little details we will run into in Chapter 2.

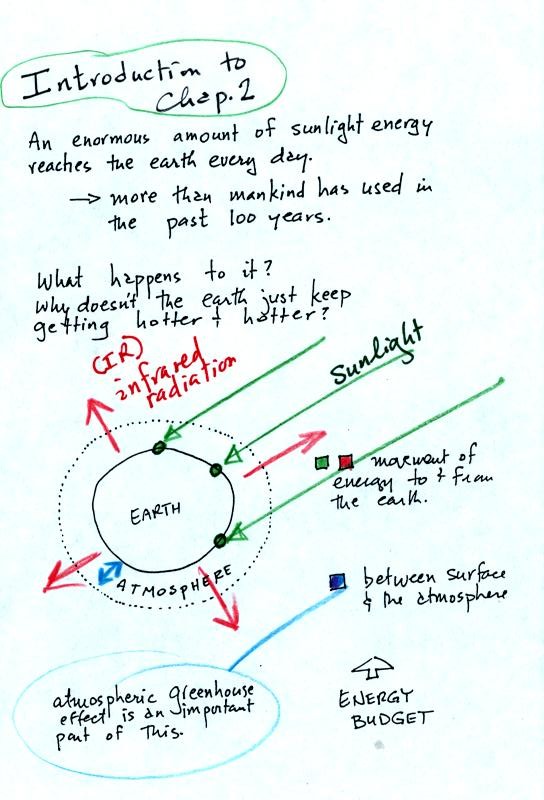
An enormous amount of sunlight energy reaches the earth everyday. We will learn how it is possible for this form of energy to travel through empty space. We know about this sunlight energy because we can see it (at some of it) and can feel it (you get warm when you stand in the sunlight). With all of this energy arriving at and being absorbed by the earth, what keeps the earth from getting hotter and hotter? The answer is that the earth also sends energy back into space. This infrared light is an invisible form of energy; we don't usually feet it either). A balance between incoming and outgoing energy is achieved and the earth's annual average temperature remains constant.

We will also look closely at energy transport between the earth's surface and the atmosphere. That is where the atmospheric greenhouse operates. That will be a major goal in Chapter 2 - to understand the atmospheric greenhouse effect.

Water vapor is a particularly important form of invisible energy. When water vapor condenses to produce the water droplets in a cloud, an enormous amount of energy is released into the atmosphere.

It is hard to visualize or appreciate energy released into the atmosphere during condensation. You can imagine the work that you would do carrying a gallon of water (8 pounds) from Tucson to the top of Mt. Lemmon, however. To accomplish the same thing Mother Nature must first evaporate the water and (if my calculations are correct) that requires about 100 times the energy that you would use to carry the 8 pounds of water to the summit of Mt. Lemmon. And Mother Nature transports a lot more than just a single gallon.

Kinetic energy is energy of motion. Latent heat energy is an unappreciated form of energy.

The four energy transport processes are listed at the bottom of the page above. By far the most important process is electromagnetic radiation. This is the only process that can transport energy through empty space. Electromagnetic radiation is also responsible for about 80% of the energy transport between the ground and atmosphere. You might be surprised to learn that latent heat is the second most important transport process.

One of the main objectives in Chapter 2 to understand the greenhouse effect.

We next covered the material on p. 45 in the photocopied class notes. I've taken that information and split it into two separate pages. When you add energy to an object, the object will usually warm up. Below we work out the equation that connects energy added and the resulting temperature change. The equation can also be used when energy is removed from an object. In that case the object will cool.

When you add energy to something the temperature change will depend on how much energy was added. So delta E is in the numerator of the equation. When you add equal amounts of energy to a small pan of water and to a large pan of water, the small pan will heat up more quickly. The temperature change, delta T, will depend on the mass. A large mass will mean a small delta T, so mass should go in the denominator of the equation. Different materials react differently when energy is added to them. A material will a large specific heat will warm more slowly than a material with a small specific heat. Specific heat behaves in the same kind of way as mass. Specific heat is sometimes called "thermal mass."

An object will usually warm when you add energy to it. But there is another possibility (mentioned at the bottom of the figure). The object could change phase. Adding energy to ice can cause the ice to melt. Adding energy to water might cause the water to evaporate.

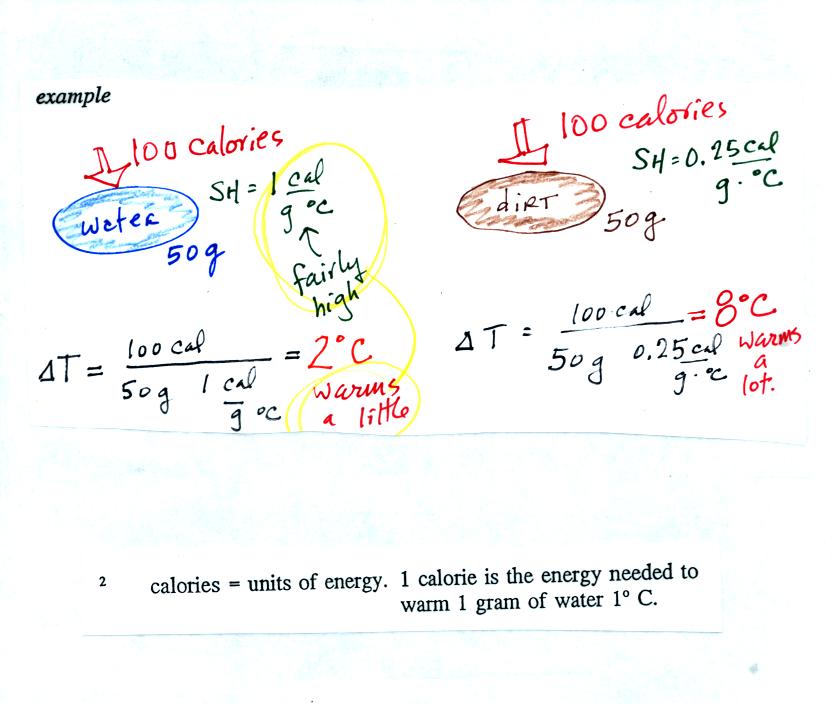
Here's an example that shows the effect of specific heat. Equal amounts of energy (note that calories are units of energy) are added to equal amounts of water and dirt. We use water and dirt in the example because most of the earth's surface is either water or dirt. Water has a higher specific heat that soil, it only warms up 2 C. The soil warms up 8 C.

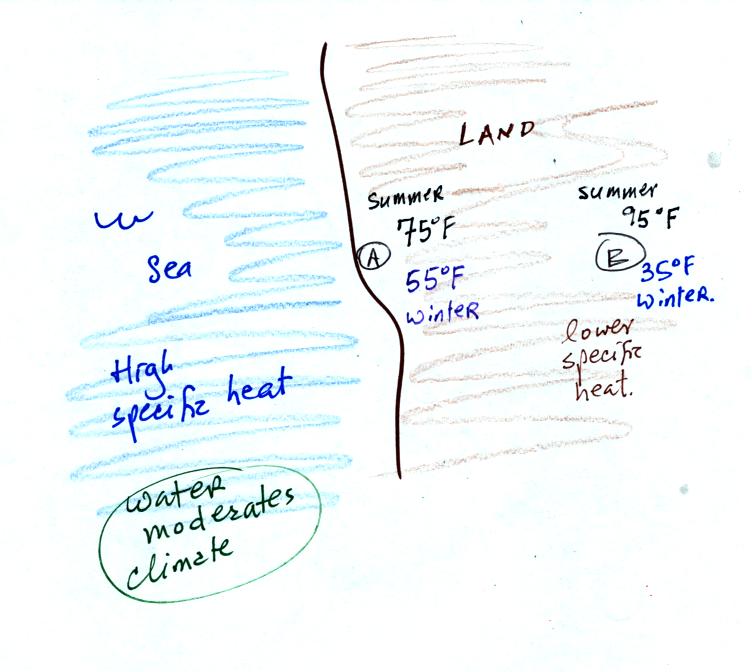
Because of its proximity to the ocean (water with high specific heat), a city on a coast won't warm up as much during the summer and won't cool as much during the winter as a city that is further inland. In the example above City A has an annual range of temperature of 20 F, in City B there is a 60 F difference between summer and winter temperatures.

OK so you add energy to an object and the object warms. What is that increase in temperature telling you about what is happening inside the material?

Temperature provides a measure of the average kinetic of the atoms or molecules in a material. You can think of heat as being the sum total kinetic energy of all the molecules or atoms in a material. The next figure might make the distinction between temperature (average kinetic energy) and heat (total kinetic energy) clearer. These next three figures weren't shown in class, they were added after class.

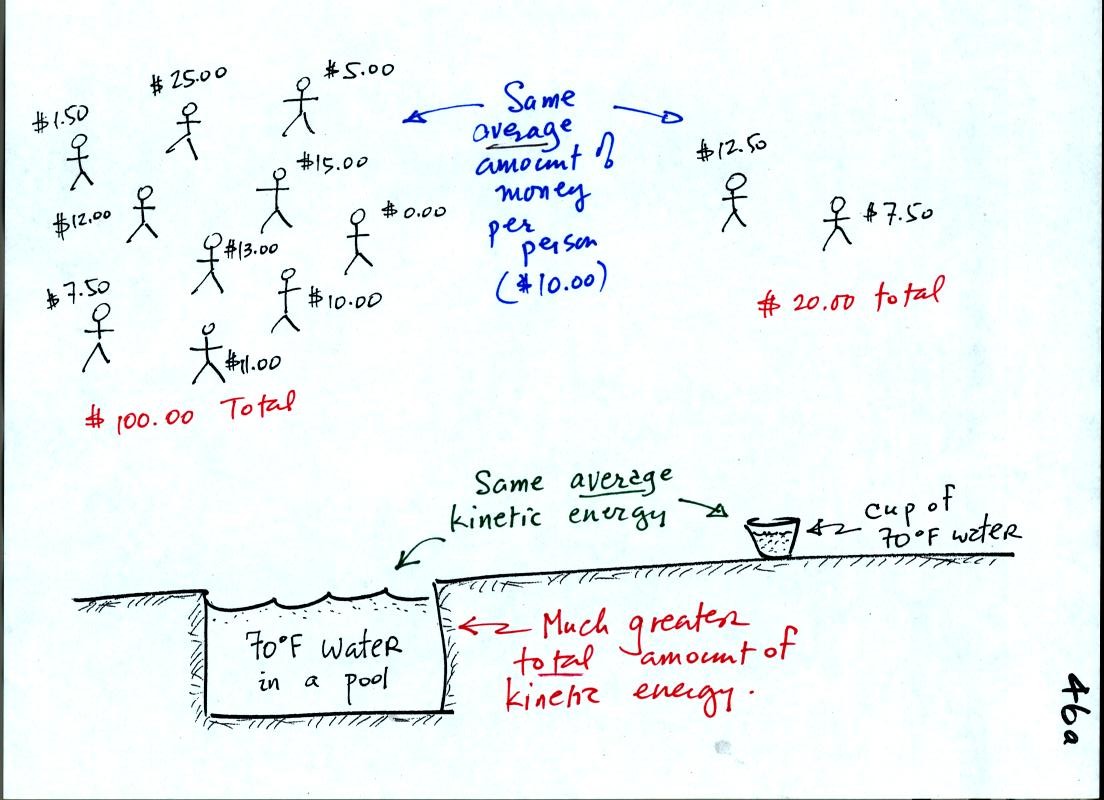
A cup of water and a pool of water both have the same temperature. The average kinetic energy of the water molecules in the pool and in the cup are the same. There are a lot more molecules in the pool than in the cup. So the total kinetic energy of all the molecules in the pool is going to be much larger than the total of all the kinetic energies in the cup.

In the same way the two groups of people have the same average amount of money per person. The $100 held by the group at the left is greater than the $20 total possessed by the smaller group of people on the right.

You need to be careful what temperature scale you use. You must use the Kelvin temperature scale because it does not go below zero.

You should remember the temperatures of the boiling point and freezing point of water on the Fahrenheit, Celsius, and Kelvin scales. A good global annual average surface temperature for the earth is 300 K.

The world high temperature record was set in Libya, the US record in Death Valley. The continental US cold temperature record of -70 F was set in Montana and the -80 F value in Alaska. The world record -129 F was measured at Vostok station in Antarctica. This unusually cold reading was the result of three factors: high latitude, high altitude, and location in the middle of land rather than near or surrounded by ocean

Now the demonstration that we did in class. We used some of what we have learned to try to measure the latent heat of vaporization of liquid nitrogen (that is the energy required to evaporate a gram of liquid nitrogen).

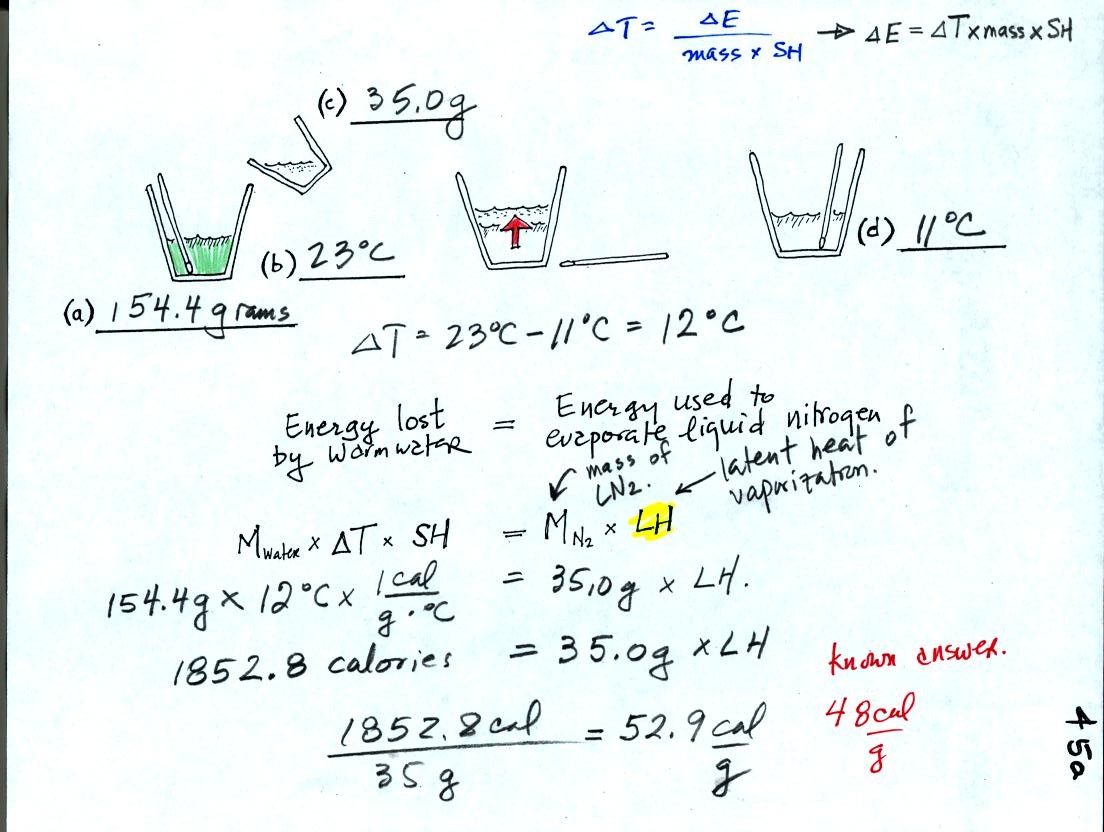
First we will make use of the Delta T vs Delta E equation (see upper right in figure above). Rather than solving for Delta T we will rearrange the equation and solve for Delta E.

We poured 154.4 grams of water into a styrofoam cup and measured its temperature (23 C). Then we weighed out 35 grams of liquid nitrogen into a second cup and poured it into the cup of water (after having removed the thermometer). We waited until all the liquid nitrogen had evaporated and remeasured the temperature of the water.

It takes energy to turn liquid nitrogen into gaseous nitrogen. The needed energy came from the water. When energy is removed from the water the water cools. By measuring how much the water cooled and knowing how much water we had we can calculate how much energy was given up by the water. That is the 1852.8 calorie figure above. This was used to evaporate 35 grams of liquid nitrogen. So 52.9 calories was needed per gram. That is our measured value. The know value is 48 cal/g, so our measurement was reasonably close to the known value.

Many people are currently trying to measure the latent heat of fusion of ice (the energy required to melt a gram of ice). The procedure they are following is similar to what we did in this demonstration.