Mon., Oct. 15 notes

Monday Oct. 15, 2007

The graded Experiment #2 reports were returned today. Revised reports will be due in two weeks - on Mon. Oct. 29 Please return your original report with your revised report.

Optional Assignment #4 (Controls of Climate) is due at the beginning of class this coming Wednesday. Copies of the assignment are available in PAS 588.

Optional Assignment #5 (Humidity) was handed out today and will be due at the beginning of class next Monday, Oct. 22.

We will first list the 4 humidity variables introduced in class last Friday.

This is a good place to put the answers to the in-class optional assignment from last Friday.

Today we will try to understand why it is possible to saturate air with water vapor. Why is there an upper limit to the amount of water vapor that air can contain? Why does this upper limit depend on air temperature?

First we need to understand that the rate at which water evaporates depends on the water's temperature.

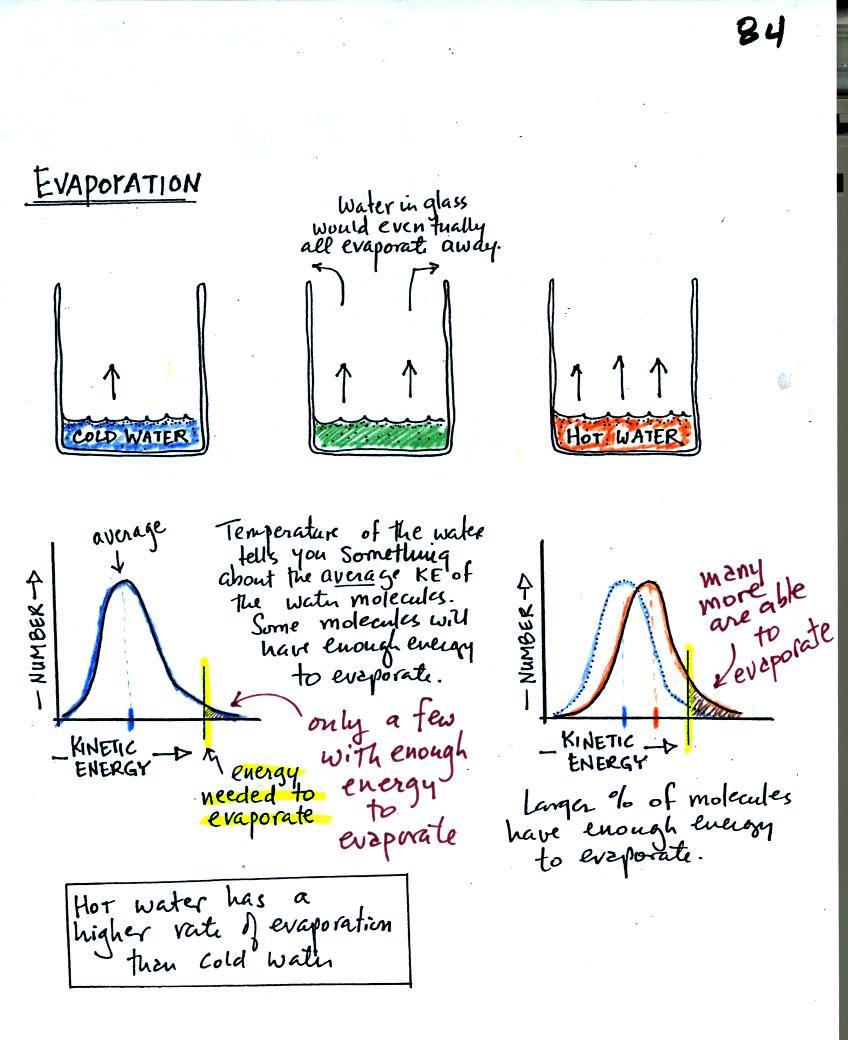
How water evaporates more rapidly than cold water. Picture a cup of hot steaming coffee and a glass of iced tea.

To be able to evaporate, a water molecule in a glass must make its way up to the surface of the water and the water molecule must then have sufficient kinetic energy (to overcome any attractive forces trying to keep it in a liquid state).

The distributions of the kinetic energies of the water molecules in the glasses of cold and hot water (remember temperature is a measure of the average kinetic energy) are shown in the two graphs above. In cold water only a limited number of the water molecules (those to the right of the highlighted line) have the necessary energy - cold water has a low rate of evaporation. In hot water, the whole distribution has moved to the right, the threshold energy needed to evaporate has remained the same, and a larger fracton of the water molecules will have enough energy. Hot water evaporates more rapidly.

Now we will look at the top part of p. 85 in the photocopied notes. We have put a cover on the glass of room temperature water.

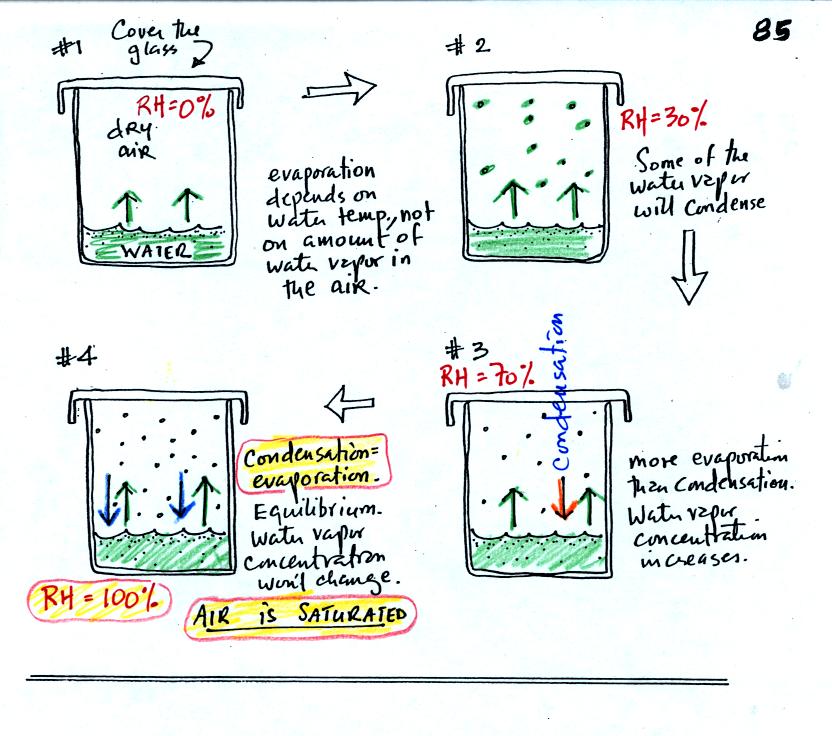
In #1 we see that the water is evaporating (2 arrows worth of evaporation). Water vapor will begin to build up in the air in the glass. This is shown in #2. Some of the water vapor molecules will condense (molecules that find themselves with lower than average kinetic energy). In Fig. #3 the amount of water vapor has built up to a point where the amount of condensation is becoming significant and one arrow worth of condensation has been added to the picture. In #3 there is still more evaporation than condensation so the water vapor concentration will increase a little bit more. Eventually in #4 the water vapor concentration has increased to a point that there are two arrows of condensation. This balances the 2 arrows of evaporation. The air is saturated, the air is filled to capacity. With equal rates of evaporation and condensation, the amount of water vapor in the air will now remain constant. Note that the relative humidity is 100% at this point. The air is filled to capacity.

What would happen if we took off the cover and added some more water vapor to the glass in Fig. #4? (this figure wasn't shown in class).

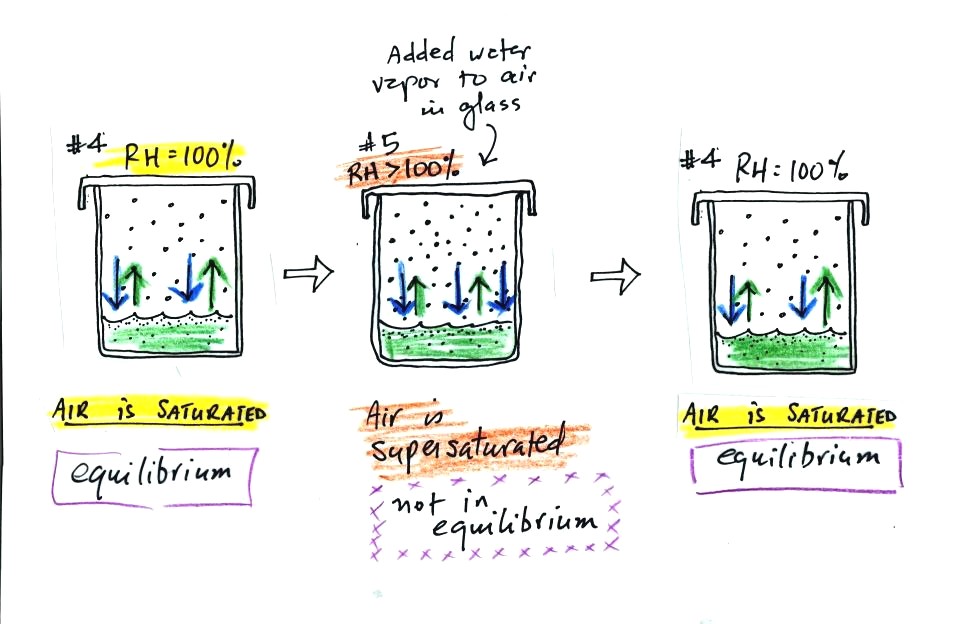
The air in Fig. #5 shows what would happen. The air would be supersaturated with water vapor and the RH would be greater than 100%. This is possible but it is not an equilibrium situation and wouldn't remain this way. The increased amount of water vapor would increase the rate of condensation. There would be more condensation than evaporation. The water vapor concentration would begin to decrease. Eventually the glass would return to the equilibrium situation in Fig. #4.

If we look at the bottom of p. 85 we see that the air in all three cases is saturated (equal rates of evaporation and condensation in each case). The relative humidity is 100% in all three cases. But because the different rates of evaporation (in cold and warm water) require different rates of condensation to be in balance, the of water vapor in the air in the two cases however is different. The warm air contains a lot more water vapor than the cold air.

At this point in class we took a short "break" and looked briefly at Experiment #3.

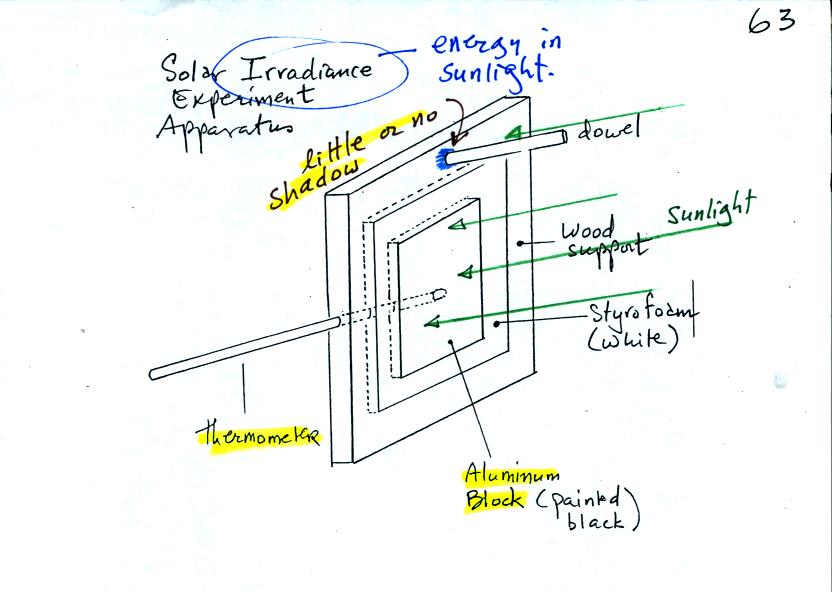
The object of Expt. #3 is to measure the energy in sunlight. The basic idea, shown in the figure below (see p. 63 in the photocopied Class Notes) and in two short video tapes (that were hopefully much clearer), is to point a flat piece of aluminum (with known area, mass, and specific heat) straight at the sun and measure how quickly it warms up.

Doesn't it seem reasonable to think that, since it is the sunlight that is causing the aluminum to warm up in the first place, you could use the temperature data to figure out how much energy is in that sunlight? [the answer to that question is Yes it does seem reasonable, very reasonable]

The problem is going from an idea that seems reasonable to an equation that you can actually use. We didn't really work out all the details in class but it's not that difficult. Click on this solar irradiance link if you are interested in seeing the details.

Now back to humidity

In the time remaining in class we were able to work a couple of humidity example problems. By doing these problems (and we'll do a couple more on Wednesday) you should become more familiar with the humidity variables (mixing ratio, saturation mixing ratio, relative humidity, and dew point temperature). You'll also learn "how they behave" and what can cause each of these variables to change value.

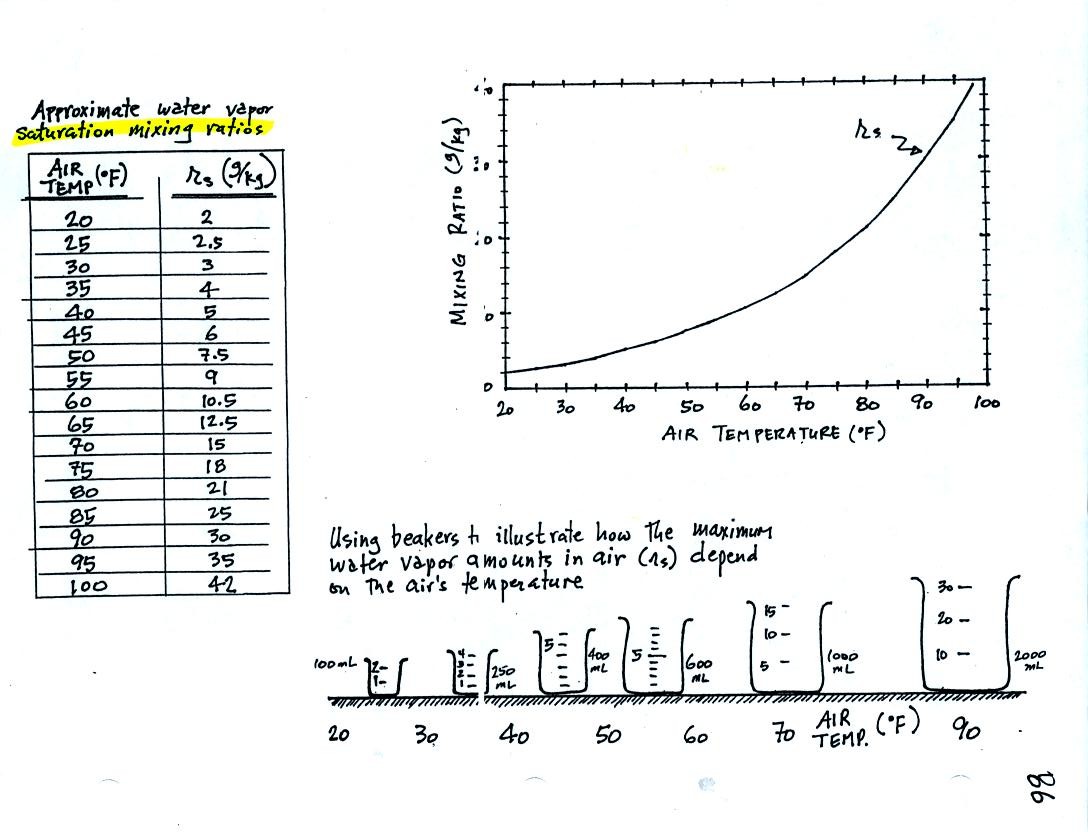
Keep this compilation of saturation mixing ratio values (shown in a table and on a graph) handy, we will use it a lot as we work through the humidity problem examples. Remember that saturation mixing ratio is the maximum amount of water vapor that can be found in air. It is a property of the air and depends on the air's temperature.

The beakers (beakers were also brought to class) are meant to show graphically the relative amounts of water vapor that air at different temperatures can contain.

Now the first of our example problems

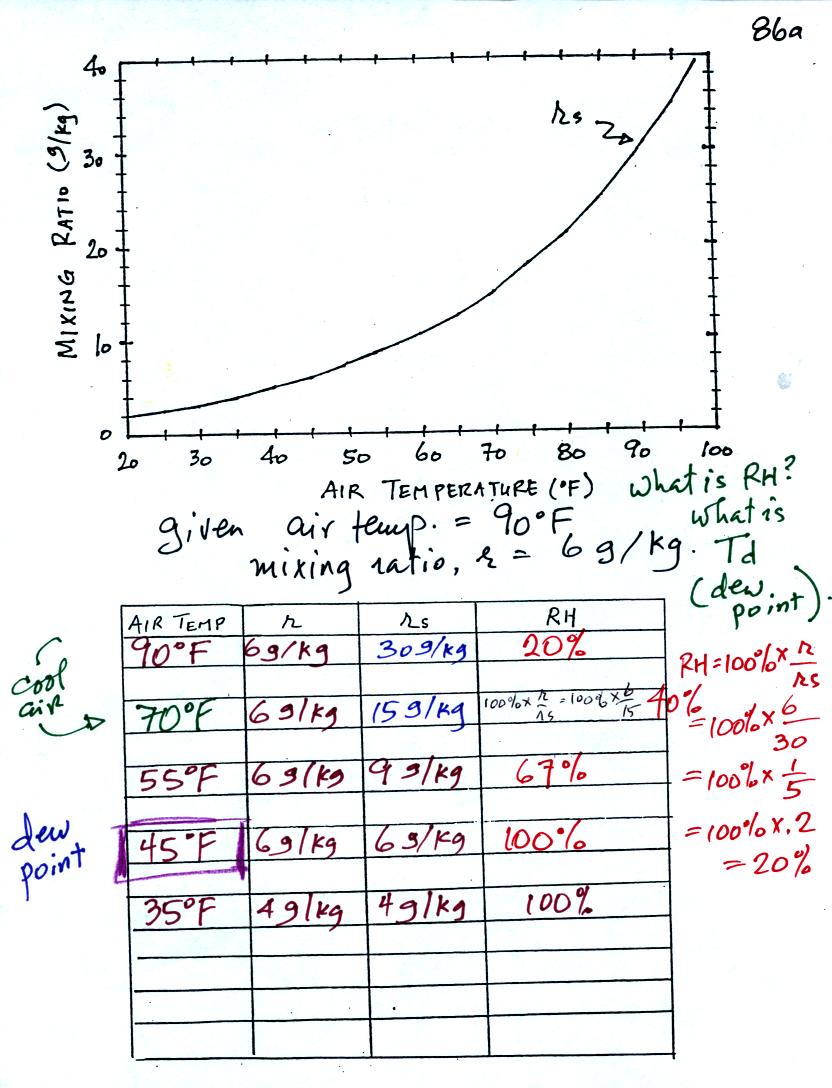
Here is the first sample problem that we worked in class. You might have a hard time unscrambling this if you're seeing it for the first time. The series of steps that we followed are retraced below:

We're given an air temperature of 90 F and a mixing ratio (r) of 6 g/kg. We're supposed to find the relative humidity (RH) and the dew point temperature.

We start by entering the data we were given in the table. Once you know the air's temperature you can look up the saturation mixing ratio value; it is 30 g/kg for 90 F air. 90 F air could potentially hold 30 grams of water vapor per kilogram of dry air (it actually contains 6 grams per kilogram in this example).

Once you know mixing ratio and saturation mixing ratio you can calculate the relative humidity. The RH is 20%.

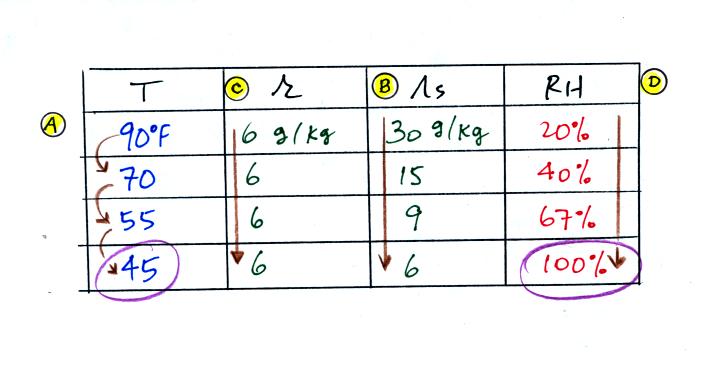
The numbers we just figured out are shown on the top line above.

(A) We imagined cooling the air from 90F to 70F, then to 55F, and finally to 45F.

(B) At each step we looked up the saturation mixing ratio and entered it on the chart. Note that the saturation mixing ratio values decrease as the air is cooling.

(C) The mixing ratio doesn't change as we cool the air. The only thing that changes r is adding or removing water vapor and we aren't doing either.

(D) Note how the relative humidity is increasing as we cool the air. The air still contains the same amount of water vapor it is just that the air's capacity is decreasing.

Finally at 45 F the RH becomes 100%. The dew point temperature in this problem is 45 F.

What would happen if we cooled the air further still, below the dew point temperature?

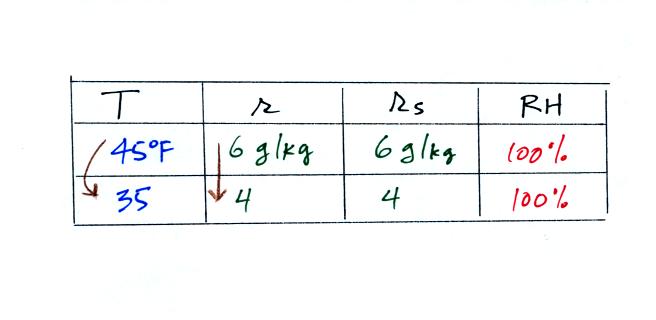
35 F air can't hold the 6 grams of water vapor that 45 F air can. You can only "fit" 4 grams of water vapor into the 35 F air. The remaining 2 grams would condense. If this happened at ground level the ground would get wet with dew. If it happens above the ground, the water vapor condenses onto small particles in the air and forms fog or a cloud. Now because water vapor is being taken out of the air (and being turned into water), the mixing ratio will decrease from 6 to 4. That is why the mixing ratio is changing.

In many ways cooling moist air is liking squeezing a moist sponge (the figure below wasn't shown in class)

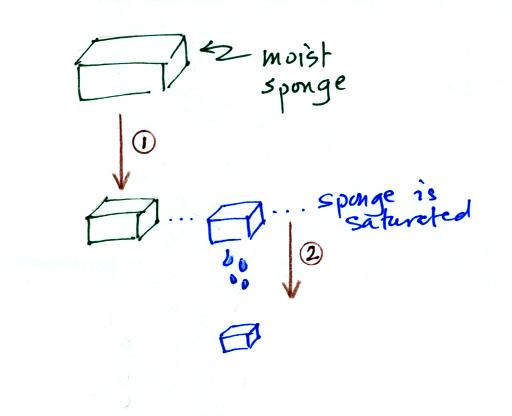
Squeezing the sponge and reducing its volume is like cooling moist air and reducing the saturation mixing ratio. At first when you sqeeze the sponge nothing happens, no water drips out. Eventually you get to a point where the sponge is saturated. This is like reaching the dew point. If you squeeze the sponge any further (or cool air below the dew point) water will begin to drip out of the sponge (water vapor will condense from the air).

Here's the 2nd problem we did

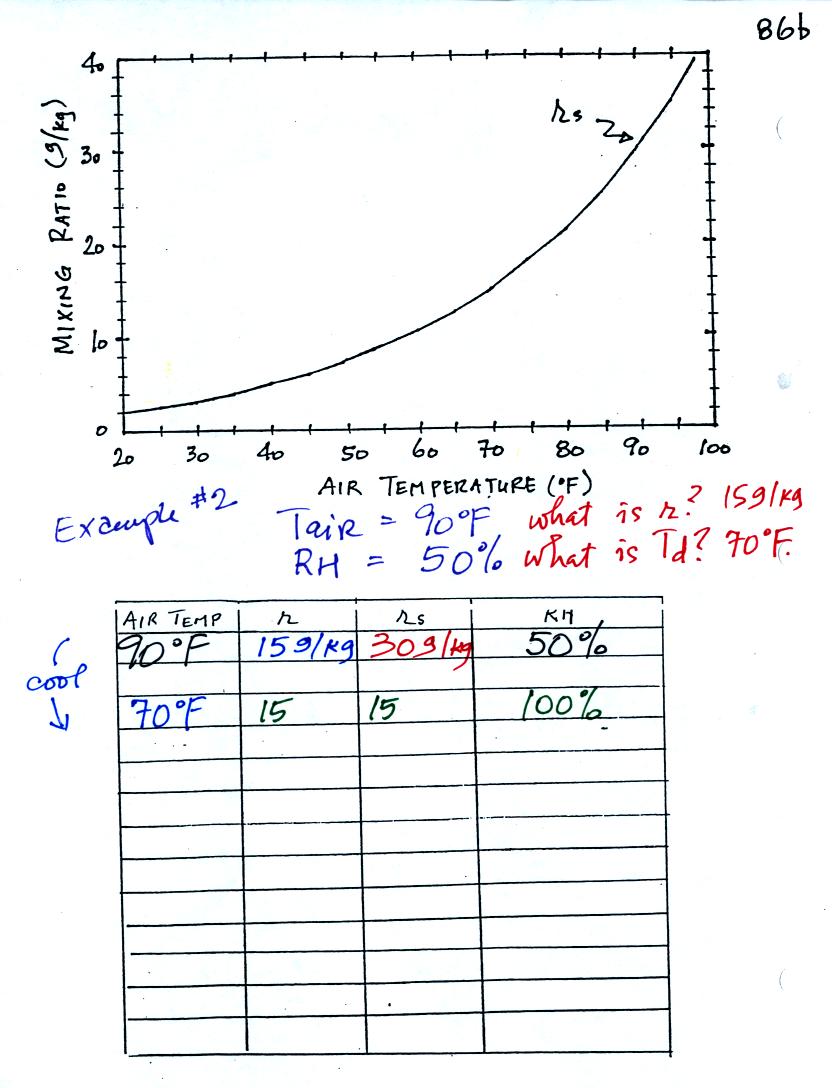
Here is what we did in class. Given an air temperature of 90 F and a relative humidity of 50% you are supposed to figure out the mixing ratio (15 g/kg) and the dew point temperature (70 F). The problem is worked out in detail below:

First you fill in the air temperature and the RH data that you are given.

(A) since you know the air's temperature you can look up the saturation mixing ratio (30 g/kg).

(B) Then you can substitute into the relative humidity formula and solve for the mixing ratio (15 g/kg).

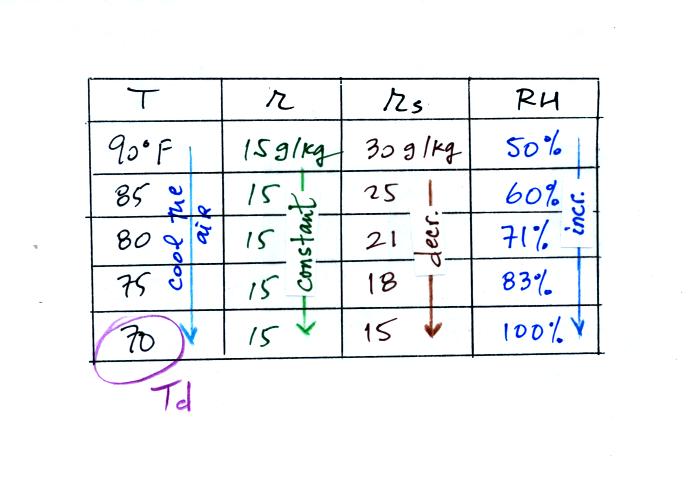
Finally you imagine cooling the air. Cooling causes the saturation mixing ratio to decrease, the mixing ratio stays constant, and the relative humidity increases. In this example the RH reached 100% when the air had cooled to 70 F. That is the dew point temperature.