Tuesday Oct. 21, 2008
Click here to download
today's notes in more printer friendly Microsoft WORD format
Rupa and the April Fishes were featured before class
today.
You'll find the two songs played in class ("Maintenant" and "Poder") at
their MySpace webpage.
You might also want to check out Une Americaine a
Paris on YouTube.
The quizzes have been graded and were returned in
class. The
average score was a little lower than Quiz #1. Check your quiz
carefully for grading erros.
An Optional Assignment turned in last week before Quiz #2
was returned
in class today. Because it covered material that was on the last
quiz it wasn't carefully graded. You probably checked the answers while you
were preparing for last week's quiz.
One group of the 1S1P Topic #3 reports has been graded and was returned
in class today. You can check to see which 1S1P reports have been
graded at this link.
1S1P Assignment #2 is now online.
Reports are due in two weeks, on or before Tuesday Nov. 4 (election
day).
A new Optional
Assignment on humidity is available online. I forgot to bring
copies of the assignment to class, I 'll have them on Thursday.
The assignment is due at the start of class next Tuesday Oct. 28.
The Experiment #2 reports should be graded by Thursday. The
revised Expt. #1 reports are due on Thursday. Please return the
original report if you turn in a revised report. Please take
advantage of the exceptional weather we are now experiencing and do
Expt. #3. Return the materials, make them available for another
student, and pick up the supplementary information sheet.
The
following is an
introduction to an important new topic: humidity (moisture in the
air). The
beginning of
Chapter 5 (pps 123-133) can be a little overwhelming and
confusing. I would suggest you skim through that material.
We reviewed this material very quickly at the start of class.
We will be mainly interested in 4 variables, what they are
and what can cause their values to change. The variables are :
mixing ratio, saturation
mixing ratio, relative humidity, and dew point. You will find
much of what follows on page 83 in the photocopied ClassNotes.
Mixing ratio tells you how much water vapor is actually in
the
air. Mixing ratio has units of grams of water vapor per kilogram
of dry air (the amount of water vapor in grams mixed with a
kilogram
of dry air). It is basically the same idea as teaspoons of sugar
mixed in a cup of tea.

The value of the mixing ratio won't change unless you add
water
vapor to or remove water vapor from the air. Warming the air
won't
change the mixing ratio. Cooling the air won't change the mixing
ratio
(unless the air is cooled below its dew point temperature and water
vapor starts to condense).
Saturation mixing ratio is just an upper limit to how much
water vapor
can be found in air, the air's capacity for water
vapor. It's a
property of air, it doesn't say anything about how much water
vapor is actually in the air (that's the mixing ratio's job).
Warm air can potentially hold more water vapor than cold air.
This variable has the same units: grams of water vapor per kilogram of
dry air. Saturation mixing ratio values for different air
temperatures are listed and graphed on p. 86 in the photocopied class
notes.
Just as is the case with water vapor in air,
there's a limit to how much sugar can be dissolved in a cup of hot
water. You can dissolve more sugar in hot water than in cold
water.
The dependence of saturation mixing ratio on air temperature is
illustrated below:

The small specks represent all of the gases in
air except
for the water
vapor. Each of the open circles represents 1 gram of water vapor
that the air could potentially hold. There are 15 open circles
drawn in the 1
kg of 70 F air; each 1 kg of 70 F air could hold up to 15 grams of
water vapor. The 40 F air only has 5 open circles; this cooler
air can only hold up to 5 grams of water vapor per kilogram of dry air.

Now we have gone and actually put some water vapor
into the
volumes of
70 F and 40 F air. 3 grams of water vapor have been added to each
volume of air. The mixing ratio, r, is 3 g/kg in both cases.
The relative
humidity is the variable most people are familiar with, it tells you
how "full" the air is with water
vapor.
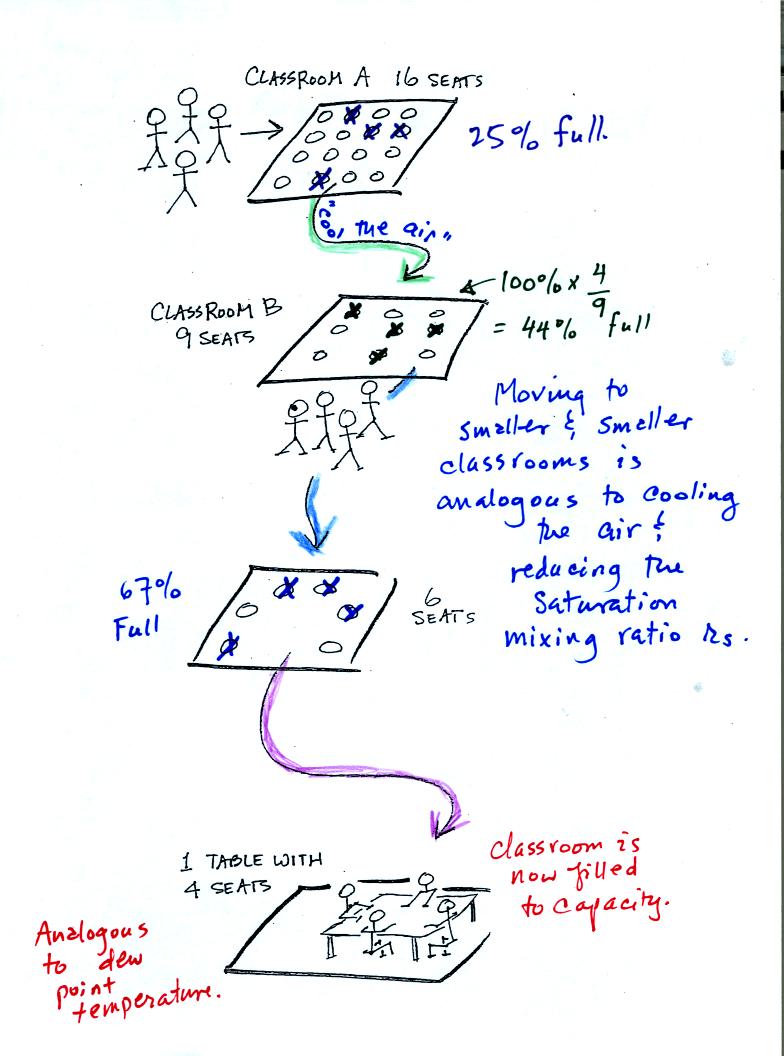
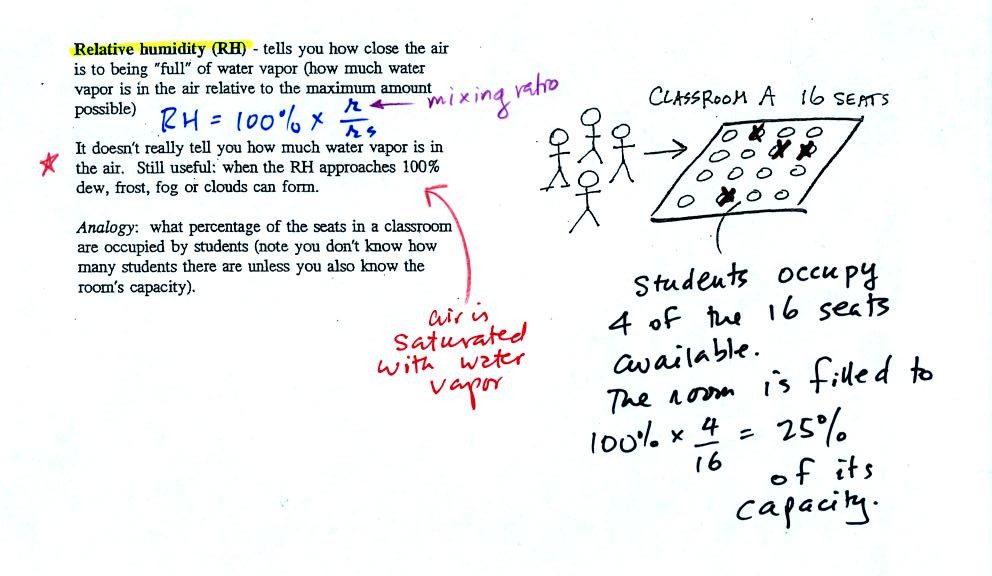
In the analogy (sketched on the right hand side of p. 83 in
the photocopied notes) 4 students wander into Classroom A which has 16
empty
seats. Classroom A is filled to 25% of its capacity.
You can think of 4, the number of students, as being analogous to the
mixing ratio. The classroom capacity is analogous
to the
saturation mixing ratio. The percentage occupancy is analogous to
the relative humidity.
Instead of students and a classroom you
could think of the 70 F and 40 F air that could potentially hold 15
grams or 5 grams, respectively of water vapor.
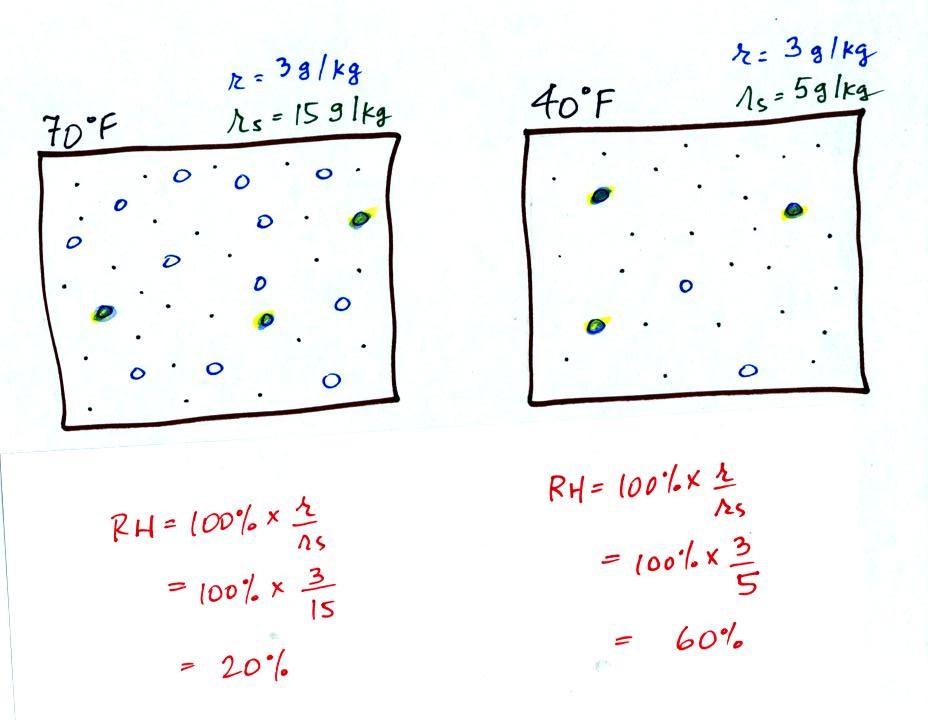
Here are the relative humidities of the 70 F and 40 F air
that each
contain 3 grams of water vapor. The 70 F air has a low RH because
this warm air's saturation mixing ratio is large. The RH in the
40 F is higher even though it has the same actual amount of water vapor
because the 40 F air can't hold as much water vapor and is closer to
being saturated. Here is a
hidden Optional Assignment that covers this introductory material on
humidity variables. The assignment will be due at the start of
class next Tuesday.
Something important to note: RH doesn't really tell you how much water
vapor is
actually in the air. The two volumes of air above contain the
same amount of water vapor (3 grams per kilogram) but have different
relative humidities. You could just as easily have two volumes of
air with the same relative humidities but different actual amounts of
water vapor.

The dew point temperature has two jobs. First it is a
measure of
the actual amount of water vapor in the air. In this respect it
is just like the mixing ratio. If the dew point temperature is
low the air doesn't contain much water vapor. If it is high the
air contains more water vapor.
Second the dew point tells you how much you must cool the air in order
to cause the RH to increase to 100% (at which point a cloud, or dew or
frost, or fog would form).
If we cool the 70 F air or the 40 F air to 30 F we would
find that the
saturation mixing ratio would decrease to 3 grams/kilogram. Since
the air actually contains 3 g/kg, the RH of the 30 F air would become
100%. The 30 F air would be saturated, it would be filled to
capacity with water vapor. 30 F is the dew point temperature for
70 F air that contains 3 grams of water vapor per kilogram of dry
air. It is also the dew point temperature for 40 F air that
contains 3 grams of water vapor per kilogram of dry air.Because
both volumes of air had the same amount of water vapor,
they both also have the same dew point temperature.
Now back to our students and classrooms analogy on the
righthand
side of p. 83. The 4 students
move into classrooms of smaller and smaller capacity. The
decreasing capacity of the classrooms is analogous to the
decrease in saturation mixing ratio that occurs when you cool
air. Eventually the students move into a classroom that they just
fill to capacity. This is analogous to cooling the air to the dew
point temperature, at which point the RH becomes 100% and the air is
filled to capacity, the air is saturated with water vapor.
Today's class featured a Survivor-like Reward Challenge.
Several students were able to win prizes by answering a few relatively
simple questions in class. Here's the first part of the first
question.
The graph shows a reasonable distribution of end-of-semester
grades. The average appears to be about 77%. Students with
grades equal to or greater than 90.0% are exempt from the final.
A student in the class was asked the three questions at the bottom of
the figure. If 5 pts were added to everyone's overall grade, the
curve and the average grade would both shift to the right. This
rightward shift would increase the number of students that wouldn't
have to take the final exam.
This is the shifted curve.
The student answered the first three questions correctly and
was able to proceed to the second part of the question.
The next figure shows the distribution of the kinetic energies of
water molecules in a glass of water. It looks just like the grade
distribution graph. There's an average and some of the water
molecules (the ones at the far right end of the curve) have enough
kinetic energy that they can evaporate (similar to students that are
exempt from the final exam).
The student was asked three
additional questions about this kinetic energy distribution
graph. If the water were heated, would the curve shift to the
right or the left. Would the average kinetic energy move to the
right or left. Would the number of water molecules, with enough
kinetic energy to be able to evaporate, increase, decrease, or remain
the same? The student's three correct answers are shown
above. The shifted curve is shown below
The student won a prize (a plastic raingauge if I remember correctly -
which I hope wasn't too much of a disappointment).
Now what we have been able to understand (in what was hopefully a
little more entertaining than normal) is that warm water evaporates
more rapidly than cold water. This is summarized om p. 84 in the
photocopied ClassNotes.
It was time for another student and a new question (the 2nd question). A two
part question. The set up is shown below.
It was basically a question about how many people would have to be
inside the Walmart in order for the rates at which people enter (10
people per minute) and at which people leave (10% of the people inside
leave every minute) to equal. Once this balance is reached the
number of people inside the store will remain constant.
The student answered the question correctly (the details are shown
below). The student also answered a follow up question about how
the answer would change if 20 people per minute were entering the
store. The correct answer was that the number inside would
increase to 200 before the rates of people entering and leaving became
equal. This student won some catfood for her cat if I remember
correctly.
The Walmart problem is very similar to saturation of air with
water vapor which is shown on p. 85 in the photocopied
ClassNotes. What does it mean to say that air is saturated with
water vapor. Why does the saturation amount depend on temperature?

The evaporating water in Picture 1 is analogous to people entering a
Walmart store. The amount of water vapor in the air in the
covered glass will begin to increase. Some fraction of the water
vapor molecules will condense (even though it has just
evaporated). The water vapor concentration will build until the
rate of condensation balances evaporation. The air is saturated
at that point. The water vapor concentration won't increase
further. Saturated air has a relative humidity (RH) of
100%. The relative humidity
values in the figure above were added after class.
Cups filled with cold and warm water
are shown at the bottom of the figure. Because of different rates
of evaporation (slow in cold, rapid in warm water) the water vapor
concentrations at saturation are different. Cold saturated air
won't contain as much water vapor as warm saturated air.
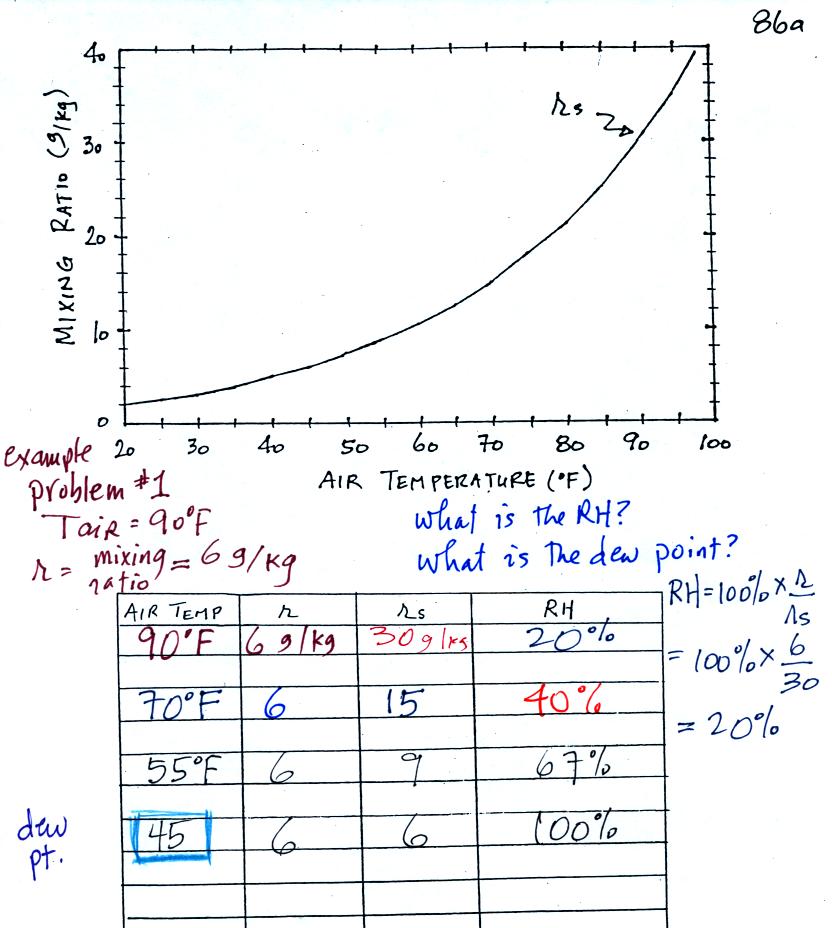
Now we are ready for 4 example problems.
Here is the first sample
problem that we worked in
class. You might have a hard time unscrambling this if
you're seeing it for
the first
time. The series of steps that we followed are retraced
below:
We're given an air temperature of 90 F and a mixing ratio
(r) of 6
g/kg. We're supposed to find the relative humidity (RH) and
the dew point temperature.
We start by entering the data we were given in the
table. Once
you know the air's temperature you can look up the saturation mixing
ratio value; it is 30 g/kg for 90 F air. 90 F air could
potentially hold 30 grams of water vapor per kilogram of dry air (it
actually contains 6 grams per kilogram in this example). The
saturation mixing ratio values are on p. 86 in the ClassNotes.
Once you know mixing ratio and saturation mixing ratio you can
calculate the relative humidity (you divide the mixing ratio by the
saturation mixing ratio, 6/30, and multiply the result by 100%).
The RH is 20%.
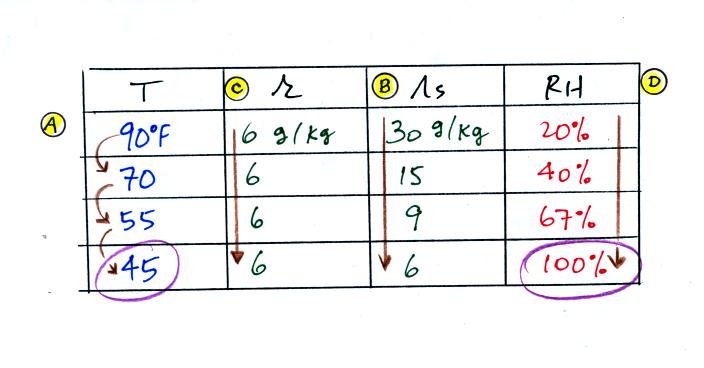
The numbers we just figured out are shown on the top line
above.
(A) We imagined cooling the air from 90F to 70F, then to 55F, and
finally to 45F.
(B) At each step we looked up the saturation mixing ratio and entered
it on the chart. Note that the saturation mixing ratio values
decrease as the air is
cooling.
The next question (3rd question)
in the class Reward Challenge was what happens to the mixing
ratio when you cool the air. A student answered this correctly
(the mixing ratio doesn't change) and won a can of Red Bull energy
drink I think.
(C) The mixing ratio doesn't
change as we cool the air. The only
thing that changes r is adding or removing water vapor and we aren't
doing either.
(D) Note how the relative humidity is increasing as we cool
the
air. The air still contains the same amount of water vapor it is
just that the air's capacity is decreasing.
Finally at 45 F the RH becomes 100%. This is kind of a special
point. You have cooled the air until it becomes saturated. The 4th question of the Reward
Challenge was what was the name given to this temperature.
The answer is dew point temperature.
The dew point temperature in
this problem is 45 F.
The student that answered this question won a compact fluorescent light
bulb.
The following question wasn't
asked in class. What would happen if we cooled the air
further still, below the dew
point temperature?

35 F air can't hold the 6 grams of water vapor
that 45 F air can. You can only "fit" 4 grams of water vapor into
the 35 F air. The remaining 2 grams would condense. If
this happened at ground level the ground would get wet with dew.
If it happens above the ground, the water vapor condenses onto small
particles in the air and forms fog or a cloud. Now because water
vapor is being taken out of the air (and being turned into water), the
mixing
ratio will decrease from 6 to 4.
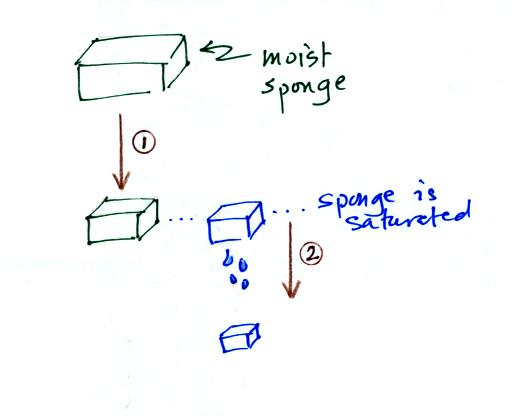
In many ways cooling moist air is liking squeezing a
moist sponge (this figure wasn't
shown in class)
Squeezing the
sponge and reducing its volume is like cooling moist air and reducing
the saturation mixing ratio. At first when you sqeeze the sponge
nothing happens, no water drips out. Eventually you get to a
point where the sponge is saturated. This is like reaching the
dew point. If you squeeze the sponge any further (or cool air
below
the dew point) water will begin to drip out of the sponge (water vapor
will condense from the air).
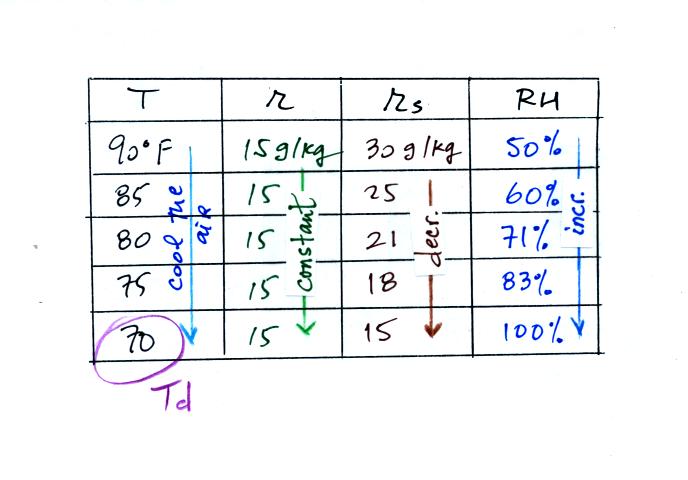
Here's the
2nd problem we worked:
The work that we did in class is shown above. Given an air
temperature
of 90
F and a relative humidity of 50% you are supposed to figure out the
mixing ratio (15 g/kg) and the dew point temperature (70 F). The
problem is worked out in detail below:
First you fill in the air temperature and the RH data that
you are
given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you can substitute into
the relative humidity formula and solve for the mixing ratio (15 g/kg).
Finally you imagine cooling the air. Cooling causes
the
saturation mixing ratio to decrease, the mixing ratio stays constant,
and the relative humidity increases. In this example the RH
reached 100% when the air had cooled to 70 F. That is the dew
point temperature.
Here's the 3rd example problem. Now that we had run out of
prizes this isn't much fun anymore. Fortunately once you've
worked a couple of problems they go much faster.
Here's the play by play solution to the question
You are given a
mixing ratio
of 10.5 g/kg and a relative humidity of 50%. You need to figure
out the air temperature and the dew point temperature.
(1) The air contains 10.5 g/kg of water vapor, this is 50%,
half, of what the air
could potentially hold. So the air's capacity, the saturation
mixing ratio must be 21 g/kg (you can either do this in your head or
use the RH equation following the steps shown).
(2) Once you know the saturation mixing
ratio you can look up the air temperature in a table.
(3) Then you
imagine cooling the air until the RH becomes 100%. This occurs at
60 F. The dew point is 60 F.
Problem #4
is probably the most difficult of the bunch.
Here's what we did in class, we
were given the air temperature and the dew point temperature. We
were supposed to figure out the mixing ratio and the relative
humidity. An attentive student pointed out that I had misread the
saturation mixing ratio value for 50 F air. It should be 7.5 not
9. The error is corrected above and the correct saturation mixing
ratio is used below.
We enter the two temperatures onto a chart and look up the
saturation
mixing ratio for each.
We ignore the fact that we don't know the mixing
ratio. We do know that if we cool the 90 F air to 50 F the RH
will
become
100%. We can set the mixing ratio equal to the value of the
saturation mixing ratio at 50 F, 7.5 g/kg. A student was able to
figure all of this out in the
last question of the challenge and won a box of colored pencils
(the best prize of the day in my opinion).
Remember back to the three earlier examples. When we
cooled air
to the the dew point, the mixing ratio didn't change. So the
mixing ratio must have been 7.5 all along. Once we know the
mixing ratio in the 90 F air it is a simple matter to calculate the
relative humidity, 25%.
I don't know about you but I enjoyed the Reward Challenge and
would like to do it again. If you have any good ideas for prizes
let me know.
I mentioned how I would like to offer a really big prize at the end of
the semester (a 5 night all expenses paid trip to Paris for two or
something like that). That is becoming more and more attractive
especially because one of the conditions in the fine print would be the
requirement that your NATS 101 instructor be the 2nd person.