Fri., Oct. 2, 2009
click here to download today's notes in
a more printer friendly format
Three songs ( "Guku", "Messages," and "Better People" )from Xavier Rudd to get things
started today in NATS 101. You'll find all three songs on his
MySpace page.
Optional Assignment #1 was returned today. If you don't have a
grade marked on your page it means you earned full credit on the
assignment (0.5 extra credit points).
In the next week or so we will be learning about several different
forms of energy, energy transport, and the atmospheric greenhouse
effect. Class started with a little bit of an overview before getting into the details.
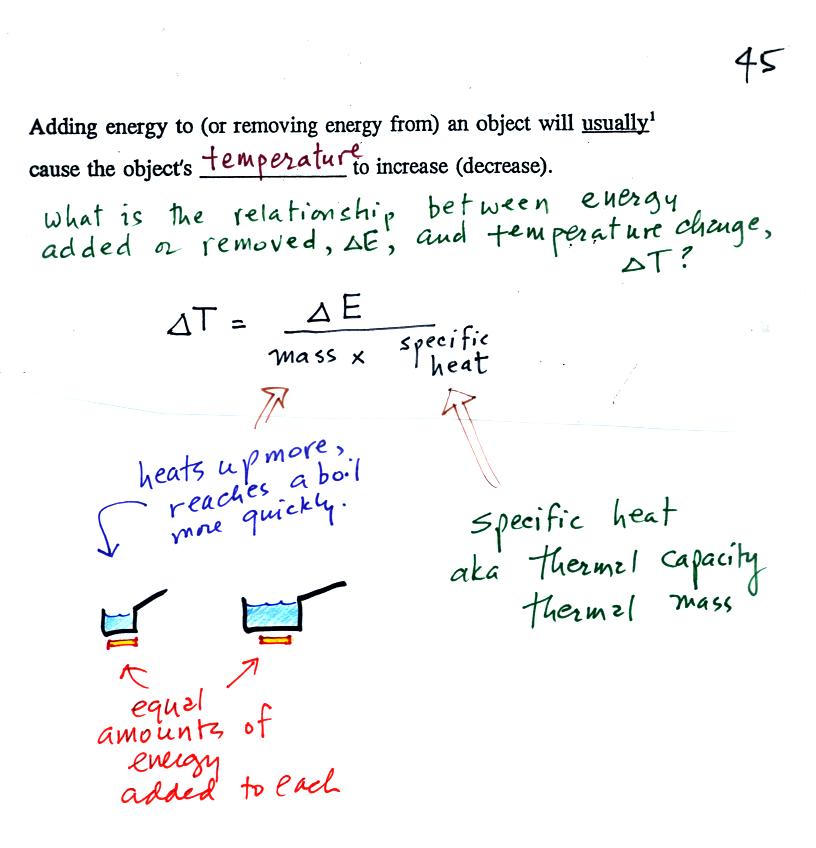
When you
add energy to an object, the object will usually
warm
up (conversely when you take energy from an object the object will
cool). It is relatively easy to come up with an equation that
allows
you to figure out what the temperature change will be.
The temperature change will
first depend on
how much energy was added. This is a direct proportionality, so
delta E is in the numerator of the
equation (delta E and delta T are both positive when energy is added,
negative when energy is taken from something)/
When you add equal amounts of energy to large and small pans
of water, the small pan will heat up more
quickly. The temperature change, delta T, will depend on the
mass. A small mass will mean a large delta T, so mass should go
in the denominator of the equation.
Different materials
react differently when energy is added to them. A material with a
large specific heat will warm more slowly than a material with a small
specific heat. Specific heat has the same kind of effect on delta
T as
mass. Specific heat is sometimes called "thermal mass" or
"thermal capacity."
Here's an important example that will show the effect of specific
heat (middle of p. 45)
Equal
amounts of energy (750 calories, note that calories are units of
energy) are added to
equal masses (150 grams) of water and soil. We use water and soil
in the
example because most of the earth's surface is either ocean or land.
Water has a higher specific heat than soil, it only warms up 5o
C.
The soil has a lower specific heat and warms up 20o C, 4
times more
than the water.
These different rates of warming of water and soil have
important effects on regional climate.
Oceans moderate the climate.
Cities near a large body
of water won't warm as much in the summer and won't cool as much during
the winter compared to a city that is surrounded by land.
The city above on the
coast has a 30o F annual range of temperature (range is the
difference between the summer and winter temperatures). The
city further
inland (assumed to be at the same latitude and altitude) has an annual
range of 60o F. Note that both cities have the same 60o
F annual
mean temperature.
Adding
energy to an object will usually cause it to warm. But there
is another possibility (bottom p. 45), the object could change
phase (change
from solid to liquid or
gas). Adding energy to ice might cause
the
ice to melt. Adding energy to water could cause it to evaporate.
The equation at the bottom of the figure above allows you to
calculate how much energy is required to melt ice or evaporate water or
sublimate dry ice. You multiply the mass by the latent heat, a
variable that depends on the particular material that is changing
phase.
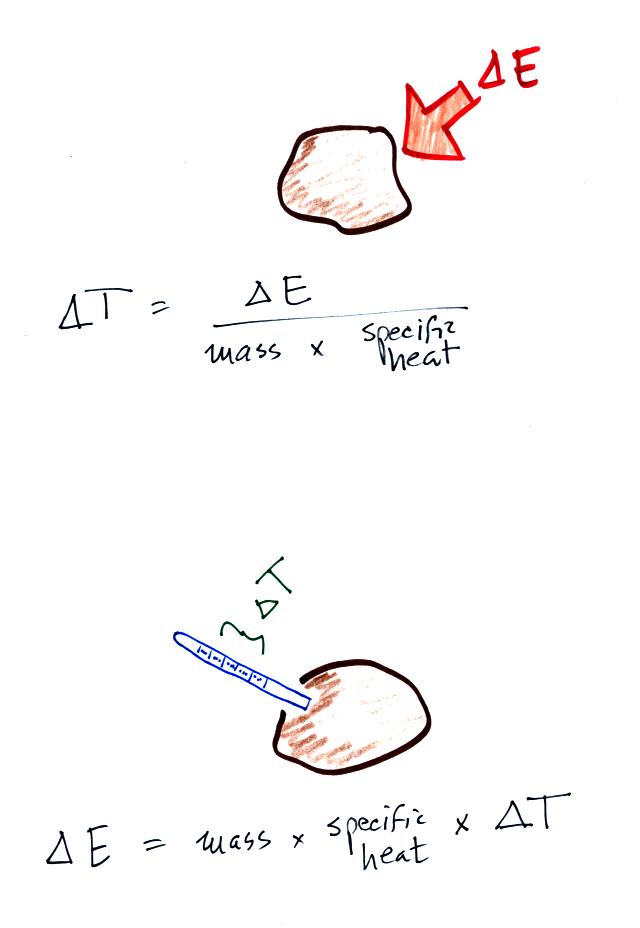
If you add energy to or remove energy from an object, the
object
will usually change temperature. You can calculate the
temperature change if you know the object's mass and its specific
heat.
We will be using the equation in a slightly different way in a class
experiment/demonstration. We will measure the temperature change and
use that to
determine the amount of energy lost by an object.
The object of the experiment was to
measure the latent heat of
vaporization of liquid nitrogen. That just means measuring the
amount of energy needed to evaporate a gram of liquid nitrogen.
The students that are doing Experiment #2 are measuring the latent heat
of fusion of ice, the energy needed to melt one gram of ice.
You'll
find the following figure on p. 45a in the photocopied
Classnotes.
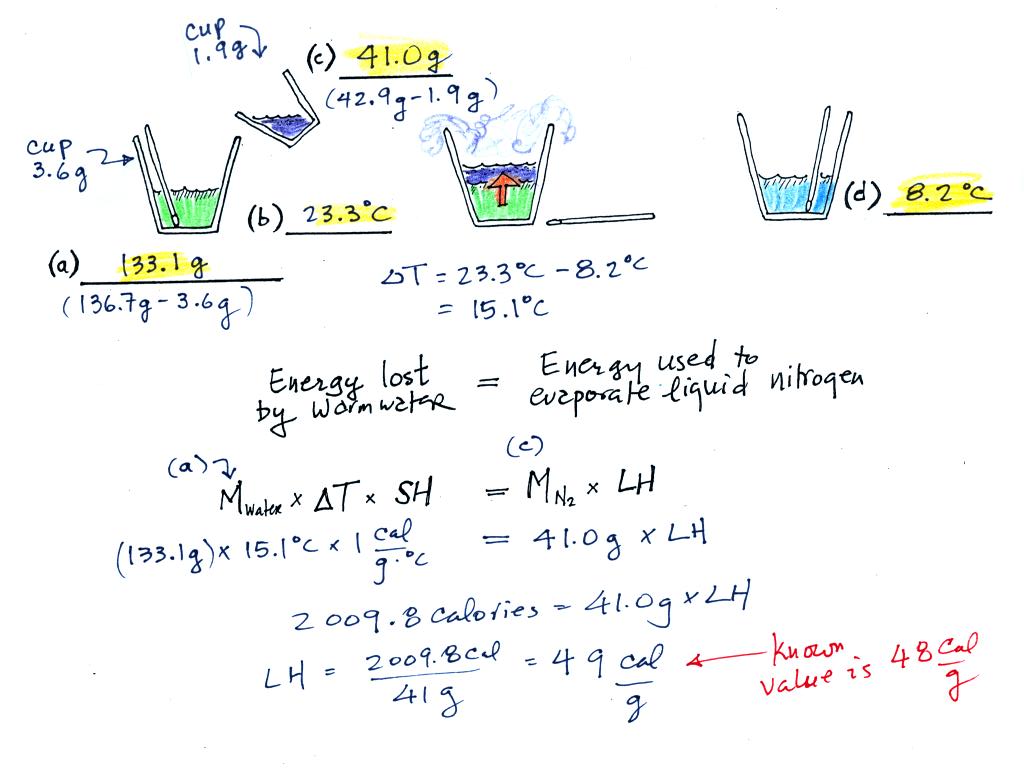
(a)
Some room temperature water poured into a styrofoam cup weighed
136.7
g. The cup itself weighed 3.6 g, so we had 133.1 g of water.
(b)
The water's temperature was 23.3 C (room temperature).
(c)
41.0 g of liquid nitrogen was poured into the cup of water.
It takes energy to turn liquid nitrogen into nitrogen gas.
The needed energy came from the water. This flow of energy is
shown in the middle figure above. We assumed that because the
experiment is performed in a styrofoam cup that there is no energy
flowing between the water in the cup and the surounding air.
(d)
After the liquid nitrogen had evaporated we remeasured the water's
temperature. It had dropped to 8.2 C. That is a
temperature drop of 23.3 - 8.2 = 15.1 C.
Because we knew how
much water we started with, its temperature drop, and water's specific
heat we can calculate how much
energy was taken from the water. That is the 2009.8 calorie
figure above. This was used to evaporate 41 grams of liquid
nitrogen. So we divided 2209.8 calories by 41 grams to get 49
calories needed per gram. That is our
measured value of the latent heat of vaporization of nitrogen. A
trustworthy student in the class informed us that
the known value is 48 cal/g, so our measurement
was pretty darn close.
We spent
the last 5 minutes of so watching another video segment documenting the
first successful non-stop flight around the globe in a balloon.
from a PBS program called
"The Great Balloon Race"
The Cable & Wireless balloon
(Andy Elson and Colin Prescot)
launch Feb. 17, 1999
Almeria, Spain
Breitling Orbiter 3 balloon
(Bertrand Piccard and Brian Jones)
launch Mar. 1, 1999
Chateau d'Oex, Switzerland
These attempts to circle the globe in a balloon were made in the winter
because the upper level winds are stronger at that time of year.