Monday Sept. 13, 2010
click here to download today's notes in a more
printer friendly format
Three songs ("Quattro
World
Drifts In", "Ballad
of Cable Hogue",
"Si Tu Disais")
from
a local group Calexico. They were appearing live at the
Barbican Theater in London with Mariachi Luz de Luna and a French
singer Francoiz Breut.
The Experiment
#1 reports are due next Monday. Try to return your materials
this week and pick up the supplementary information handout. The Experiment #2 materials will be handed out
next week.
The In-class Optional Assignments from last Friday were returned
today. If there is no grade marked on your paper you earned full
credit (0.15 extra credit points). Here are answers to
the assignment.
The first take home Optional Assignment of
the
semester is due at the start of class on Friday.
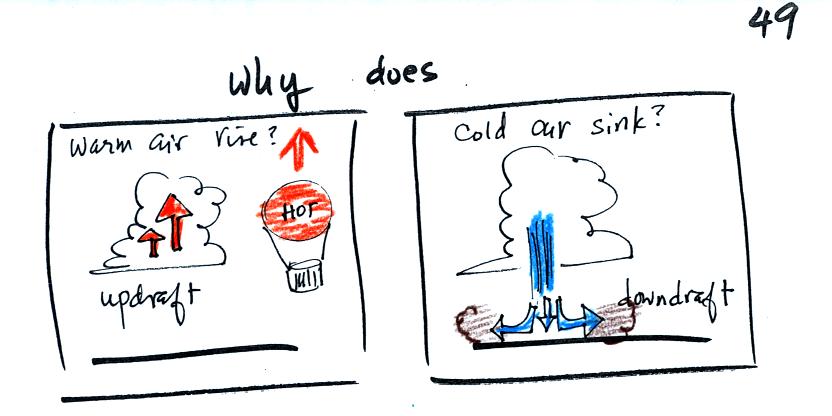
One of the questions on the
In-class Assignment asked you to identify the forces that would cause a
hot air balloon to either sink or rise. Basically we need to
understand why warm air rises and cold air
sinks.
Hot air balloons rise (they also
sink), so does the relatively
warm air in a thunderstorm (its warmer than the air around
it). Conversely cold air sinks. The surface winds
caused by a thunderstorm downdraft (as shown above) can reach speeds of
100 MPH and are a serious weather hazard.
A full understanding of these rising and sinking motions is a
3-step process (the following is
from the bottom part of p. 49 in the photocopied ClassNotes)
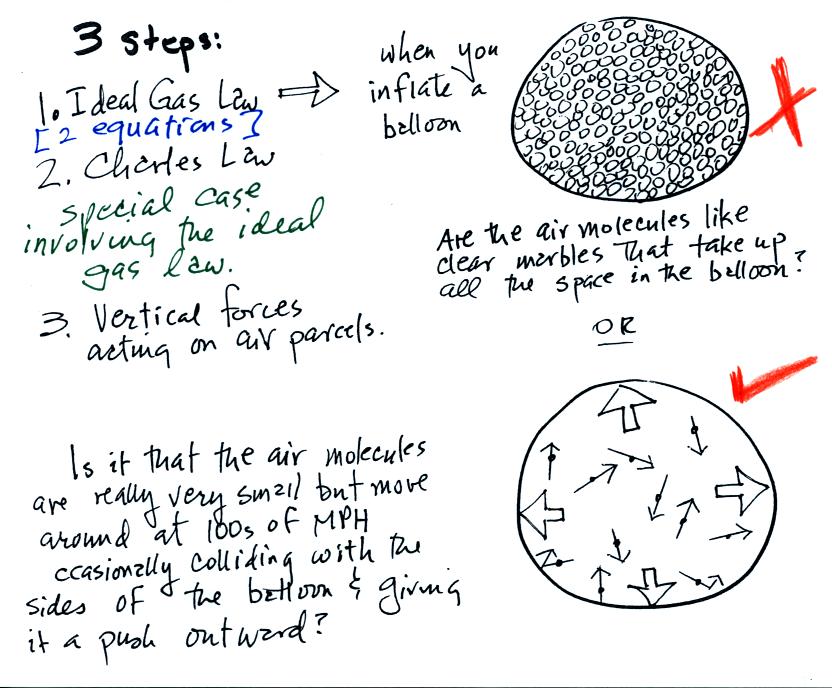
We will first learn about the ideal
gas law.
That is an equation that tells you which/how properties of the air
inside a
balloon work to determine the air's pressure. Then we will look
at Charles' Law, a special situation involving the ideal gas law (air
temperature and density change together in a way that keeps the
pressure
inside a balloon constant).
Then we'll learn about the
vertical forces that act on air (an upward
and a downward force).
Students working on Experiment #1 will need to understand the
ideal gas law to be able to explain why/how their experiment works.
The figure above makes an important point: the air molecules in a
balloon "filled with air" really take up very little space. A
balloon filled with air is really mostly empty space. It is the
collisions of the air molecules with the inside walls of the balloon
that keep it inflated.
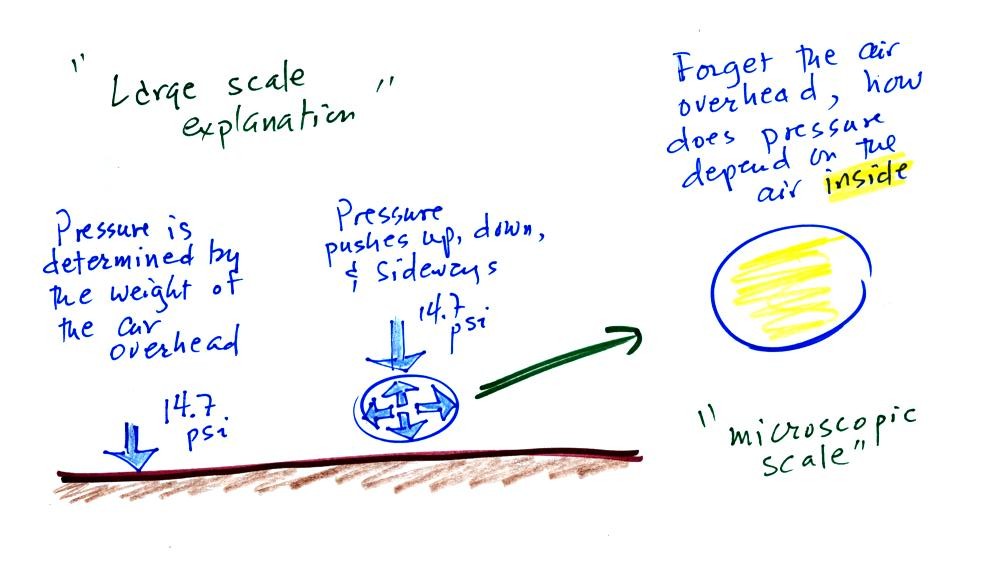
Up to this point in the semester we
have been thinking of pressure as
being determined
by the weight of the air overhead. Air pressure pushes down
against the ground at sea level with 14.7 pounds of force per square
inch. If you imagine the weight of the atmosphere pushing down on
a balloon sitting on the ground you realize that the air in the balloon
pushes back with the same force. Air everywhere in the atmosphere
pushes upwards, downwards, and sideways.
The ideal gas law
equation is another way of thinking about air pressure, sort of a
microscopic scale version. We ignore
the atmosphere and concentrate on just the air inside the
balloon. We are going to "derive" an equation. Pressure (P)
will be on the left hand side. Relevant properties of the air
inside the
balloon will be found on the right side of the equation.
In A
the pressure produced by
the air
molecules inside a balloon will
first depend on how many air molecules are there, N. If there
weren't any air molecules at all there wouldn't be any
pressure. As you add more and more add to something like a
bicycle tire, the
pressure increases. Pressure is directly proportional to N; an
increase in N causes an increase in P. If N doubles, P also
doubles (as long as the other variables in the equation don't change).
In B
air pressure inside a balloon
also
depends on the size of the
balloon. Pressure is inversely proportional to volume, V
. If V were to double, P would drop to 1/2 its original value.
Note
it
is possible to keep pressure constant by changing N and V
together in just the right kind of way. This is what happens in
Experiment #1 that some students are working on. Oxygen in a
graduated cylinder reacts with steel wool to form rust. Oxygen is
removed from the air sample which is a decrease in N. As oxygen
is removed, water rises up into the cylinder decreasing the air sample
volume. N and V both decrease in the same relative amounts and
the air sample pressure remains constant.
If you were to remove 20% of the air molecules, V would decrease
to 20% of its original value and pressure would stay constant.

Part C: Increasing
the temperature of the gas in a balloon will cause the gas molecules to
move more quickly. They'll collide with the walls of the balloon
more frequently and rebound with greater force. Both will
increase the pressure. You shouldn't throw a can of spray paint
into a fire because the temperature will cause the pressure inside the
can to increase and the can could explode.
Surprisingly, as explained in Part
D,
the pressure
does
not depend on the mass of the
molecules. Pressure doesn't depend on the composition of the
gas. Gas molecules with a lot of mass will move slowly, the less
massive molecules will move more quickly. They both will collide
with the walls of the container with the same force.
The figure below (which replaces the bottom of p. 51 in the
photocopied
ClassNotes) shows two forms of the ideal gas law. The top
equation is the one we just derived and the bottom is a second slightly
different version. You can
ignore the
constants k and R if you are just trying to understand how a change in
one of the variables would affect the pressure. You only need the
constants when you are doing a calculation involving numbers (which we
won't be doing).

Charles' Law is a special case involving the ideal gas law.
Charles Law requires that the pressure in a volume of air remain
constant. T, V, and density can change but they must do so in a
way that keeps P constant. This is what happens in the
atmosphere. A volume of air is free to expand or shrink. It
does so to keep the pressure inside the air volume constant (the
pressure inside the volume is staying equal to the pressure of the air
outside the volume).
Read through the explanation on p.
52 in the photocopied
Classnotes. In the atmosphere a parcel (balloon) of air will
always try to keep its pressure the same as the pressure of the
surrounding air. If they aren't equal the parcel will either
expand or shrink until they are again equal.
If you warm air it will expand and density will decrease until the
pressure inside and outside the parcel are equal.
If you cool air the parcel will shrink and the density will increase
until the pressures balance.
These two associations:
(i)
warm air = low
density air
(ii) cold air = high density air
are important and will come up a
lot during the remainder of the
semester.
Click here
if you
would like a little
more detailed, more step-by-step,
explanation of Charles Law. Here's a visual summary
of Charles' Law (this
figure
wasn't shown in class)
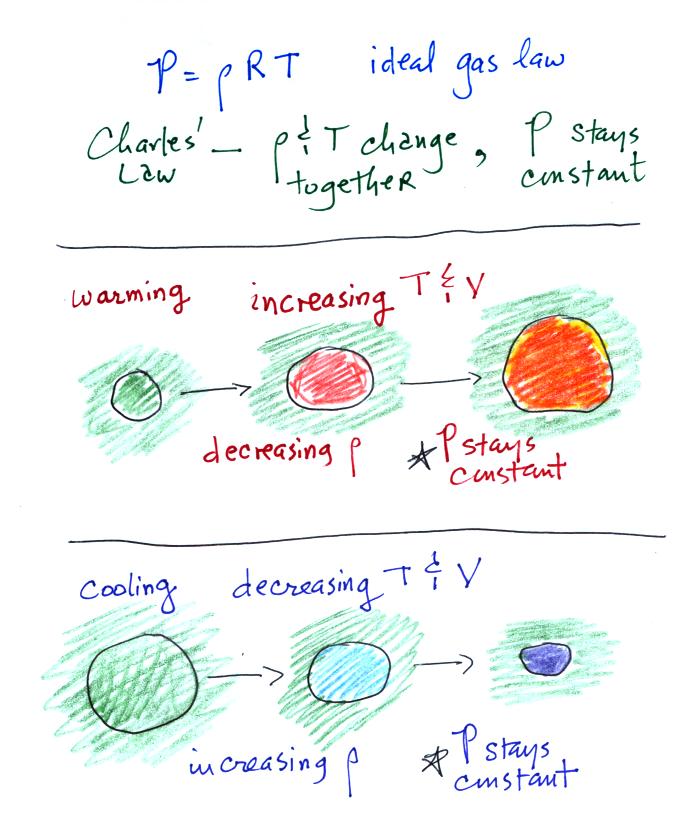
If you warm a parcel of air the
volume will increase and the density will decrease. Pressure
inside the parcel remains constant. If you cool the parcel of air
it's volume decreases and its density increases. Pressure inside
the parcel remains constant.
Charles
Law can be demonstrated by dipping a balloon in
liquid
nitrogen. You'll find an explanation on the top of p. 54 in the
photocopied ClassNotes.
The balloon had shrunk down to
practically zero volume when
pulled from the liquid nitrogen. It was filled with cold high
density air. As
the balloon warmed the balloon expanded and the density of the air
inside
the balloon decreased. The volume and temperature kept changing
in a way that kept pressure constant. Eventually the balloon ends
up back at room temperature (unless it pops while warming up).
And finally the last step toward understanding why warm air rises
and cold air sinks. We'll have a look at the forces that act on
parcels of air in the atmosphere. This information is
found on p. 53
in the photocopied
ClassNotes.
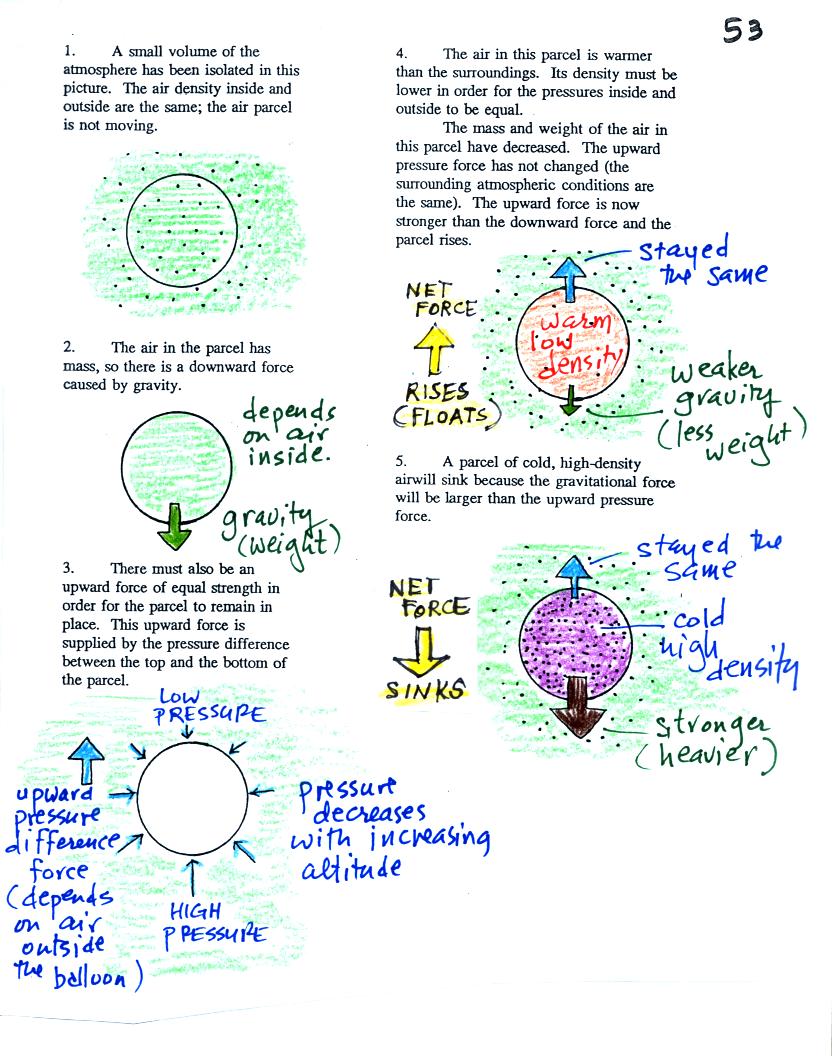
Basically it comes down to this - there are two forces
acting on a parcel* of air in the atmosphere:
1. Gravity pulls downward. The strength of the gravity force
depends
on the mass of the air inside
the parcel. This force is just the weight of the parcel
2. There is an upward pointing pressure difference force.
This
force is
caused by the air outside
(surrounding) the parcel. Pressure decreases with increasing
altitude. The pressure of the air at the bottom of a parcel
pushing upward is slightly stronger than the pressure of the air at the
top of the balloon that is pushing downward. The overall effect
is an upward pointing force.
When the air inside a parcel is exactly the same as the air
outside,
the two forces are equal in strength and cancel out. The parcel
is
neutrally bouyant and doesn't rise or sink.
If you replace the air inside the balloon with warm low density
air, it
won't weigh as much. The gravity force is weaker. The
upward
pressure difference force doesn't change (because it is determined by
the air outside the balloon which hasn't changed) and ends up stronger
than the
gravity force. The balloon will rise.
Conversely if the air inside is cold high density air, it weighs
more. Gravity is stronger than the upward pressure difference
force and the balloon sinks.
* the
word
parcel
just
means a small volume of air.