This short section will try to answer the following questions:
Why it is possible to saturate air with
water vapor?
Why is there an upper limit to the amount of water
vapor that air can contain?
Why does this upper limit depend on
air temperature?
First we need to understand that the rate at which water evaporates
depends on the water's temperature.
You can test your intuition. What would evaporate more
quickly, a glass of iced tea or a glass of hot tea?

Hot water evaporates more readily than cold water. In the
figure above (top of p. 84 in the photocopied Classnotes) the hot water
is evaporating three times more rapidly than the cold water.
To be able to evaporate, a water molecule in a glass must
make its way
up to the
surface of the water and the water molecule must then have sufficient
kinetic energy
(to overcome any attractive forces trying to keep it in a liquid
state).

The distributions of the kinetic energies of the water molecules in the
glasses of cold and hot water (remember temperature is a measure of the
average kinetic energy) are shown in the two graphs above. In
cold water only a limited number of the water molecules
(those to the right of the highlighted line) have the necessary
energy - cold water has a low rate of
evaporation. In hot water, the whole distribution has moved to
the
right, the threshold energy needed to evaporate has remained the same,
but a larger fracton of the water
molecules have moved to the right of that threshold. Hot water
evaporates more
rapidly.
Now we
will look at the top part of p. 85 in the photocopied
notes. We have put a cover on the glass of room temperature
water.

In #1 we see that the water is evaporating (2 blue arrows
worth
of
evaporation). Water vapor will begin to build up in the air in
the glass. This is shown in #2. Some of the water vapor
molecules will condense (molecules that find themselves with lower than
average kinetic energy). In Fig. #3 the amount of water vapor has
built up to
a point where the amount of condensation is becoming significant and
one orange arrow worth of condensation has been added to the
picture. In
#3
there is still more evaporation than condensation so the water vapor
concentration will increase a little bit more. Eventually in #4
the water vapor concentration has increased to a point that there are
two arrows of condensation. This balances the 2 arrows of
evaporation. The air is saturated, the air is filled to
capacity. With equal rates of evaporation and condensation, the
amount of water vapor in the air will now remain
constant. Note that the relative humidity is 100% at this point.
What would happen if we took off the cover and added some
more water
vapor to the glass in Fig. #4?
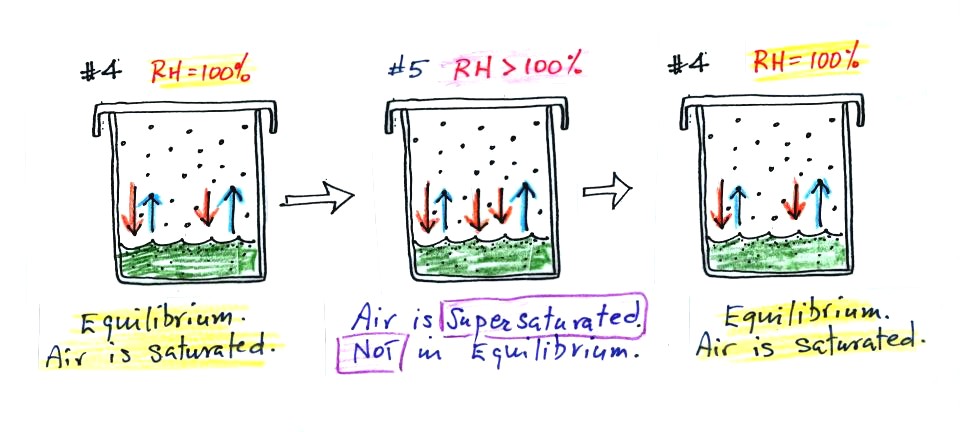
The air in Fig. #5 shows what would
happen. The
air
would be supersaturated with water vapor and the RH would be greater
than 100%. This is possible but it is not an equilibrium
situation and wouldn't remain this way. The increased amount of
water vapor would increase the
rate of condensation. There would be more condensation than
evaporation (3 orange arrows of condensation and 2 blue arrows of
evaporation in the figure above). The water vapor concentration
would begin to
decrease. Eventually the glass would return to the equilibrium
situation in Fig. #4.
We bring back the glasses of cold and hot warm at the bottom of p. 85
in the photocopied Class Notes.
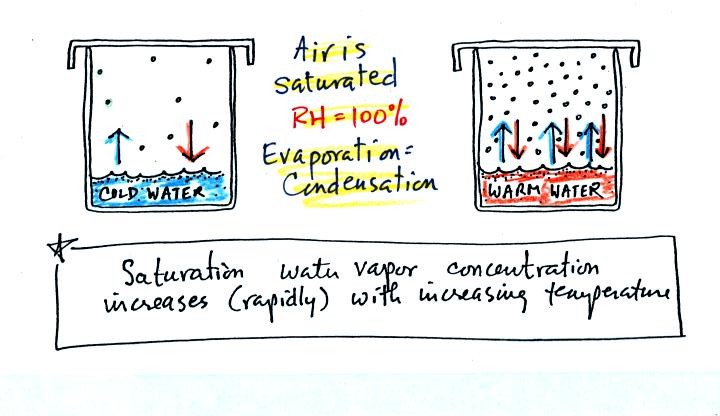
The relative humidity is 100%, and the air is saturated in
both cases. Not much water vapor is needed to provide 1 arrow of
condensation needed to balance the 1 arrow of evaporation in the cold
glass. There are 3 arrows of evaporation in the glass of warm
water. There must be a lot more water vapor in the air to provide
3 arrows of condensation.




