Often the best way to answer a
question like this is to do an experiment.
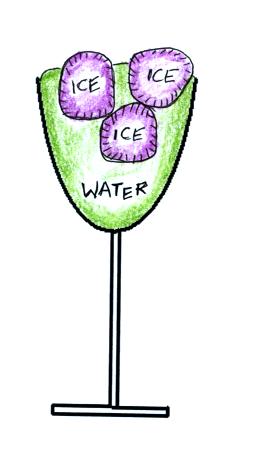
Put three or four ice cubes in a clear glass and fill the glass right up to the rim with water. The ice should be floating; don't put in so much ice that it is stacked up and pushing against the bottom of the glass. Now wait and let all the ice melt. Once that has happened you should find that the water level doesn't change.
Archimedes Law and a few more figures can help us understand why this is true.
Put three or four ice cubes in a clear glass and fill the glass right up to the rim with water. The ice should be floating; don't put in so much ice that it is stacked up and pushing against the bottom of the glass. Now wait and let all the ice melt. Once that has happened you should find that the water level doesn't change.
Archimedes Law and a few more figures can help us understand why this is true.

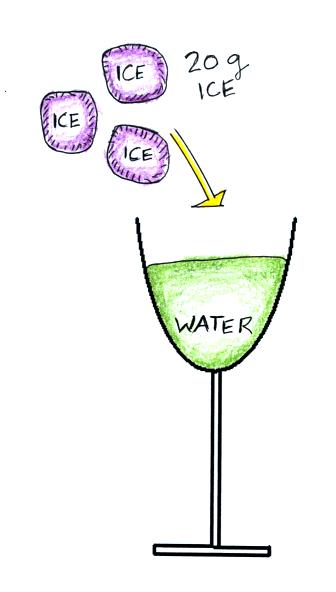
We'll imagine adding 20 grams of
ice to the glass of water. Archimedes law states that an object
immersed in a fluid will experience an upward bouyant force equal to
the weight of the fluid displaced. It's this upward force that
causes the ice to float.
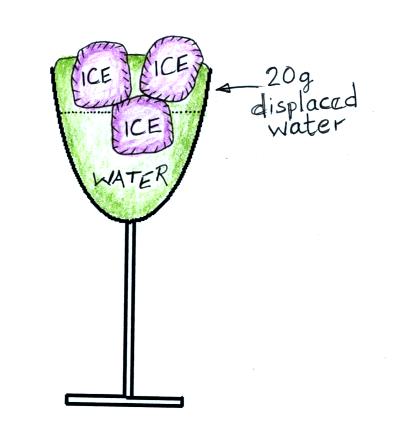
Ice has a density of about 0.9 g/cm3, a little
bit less than the density of water (1 g/cm3). The 20
grams of ice has a volume of about 22.2 cm3. Once the
ice is
added to the water, 20 cm3 of the ice will sink below the
surface of
the water; this will displace 20 grams of water (20 cm3 of
water). The upward bouyant force (the weight of 20 grams of
displaced water) is just strong enough to balance the weight of the ice
(20 grams of ice).

Once all the ice melts it will still have a mass of 20 grams. But it's volume will now be 20 cm3 instead of 22.2 cm3. So the 20 cm3 of ice water will take the space that was occupied by the 20 cm3 of submerged ice. The displaced water is now supporting 20 grams of ice water instead of 20 grams of ice. The ice cubes have all melted and the water level is the same as it was at the start of the demonstration.


Once all the ice melts it will still have a mass of 20 grams. But it's volume will now be 20 cm3 instead of 22.2 cm3. So the 20 cm3 of ice water will take the space that was occupied by the 20 cm3 of submerged ice. The displaced water is now supporting 20 grams of ice water instead of 20 grams of ice. The ice cubes have all melted and the water level is the same as it was at the start of the demonstration.