We'll spend the majority of this lecture working out some humidity example problems.  This way you will learn more about the 4 humidity variables (mixing ratio, saturation mixing ratio, relative humidity, and dew point temperature).  You'll see what they do and what can cause their values to change. 

Example 1
We're given an air temperature of 90 F and a mixing ratio (r) of 6 g/kg.  We're  supposed to find the relative humidity (RH) and the dew point temperature.   We'll start by constructing a 4-column chart (columns for air temperature, mixing and saturation mixing ratio, and dew point temperature).  We'll fill in the information we are given.


We start by entering the data we were given in the table.  Once you know the air's temperature you can look up the saturation mixing ratio value; it is 30 g/kg for 90 F air.  90 F air could potentially hold 30 grams of water vapor per kilogram of dry air (it actually contains 6 grams per kilogram in this example).  A table of saturation mixing ratio values can be found on p. 86 in the ClassNotes.

Once you know mixing ratio and saturation mixing ratio you can calculate the relative humidity (you divide the mixing ratio by the saturation mixing ratio, 6/30, and multiply the result by 100%).  You ought to be able to work out the ratio 6/30 in your head (6/30 = 1/5 = 0.2).  The RH is 20%. 


The numbers we just figured out are shown on the top line above. 

(A) We imagine cooling the air from 90F to 70F, then to 55F, and finally to 45F.

(B) At each step we looked up the saturation mixing ratio and entered it on the chart.  Note that the saturation mixing ratio values decrease as the air is cooling.

(C) The mixing ratio doesn't change as we cool the air.  The only thing that changes r is adding or removing water vapor and we aren't doing either. 

(D) Note how the relative humidity is increasing as we cool the air.  The air still contains the same amount of water vapor it is just that the air's capacity is decreasing.

Finally at 45 F the RH becomes 100%.  We have cooled the air until it has become saturated.  That's just the definition of the dew point temperature.  The dew point temperature in this problem is 45 F.

What would happen if we cooled the air further still, below the dew point temperature?


35 F air can't hold the 6 grams of water vapor that 45 F air can.  You can only "fit" 4 grams of water vapor into the 35 F air.  The remaining 2 grams would condense.  If this happened at ground level the ground would get wet with dew.  If it happens above the ground, the water vapor condenses onto small particles in the air and forms fog or a cloud.  Now because water vapor is being taken out of the air (and being turned into water), the mixing ratio will decrease from 6 to 4.

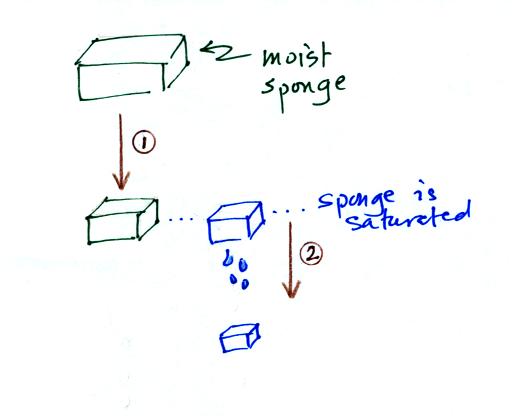
In many ways cooling moist air is liking squeezing a moist sponge.


Squeezing the sponge and reducing its volume is like cooling moist air and reducing the saturation mixing ratio.  At first when you sqeeze the sponge nothing happens, no water drips out.  Eventually you get to a point where the sponge is saturated.  This is like reaching the dew point.  If you squeeze the sponge any further (or cool air below the dew point) water will begin to drip out of the sponge (water vapor will condense from the air).

Example 2
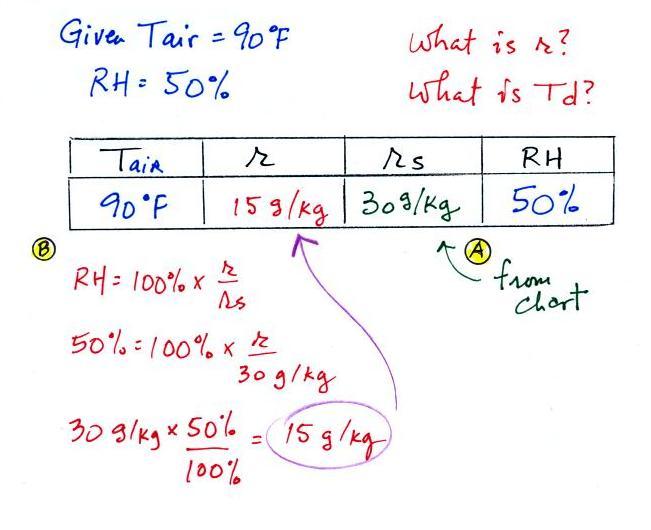
In this problem we'll start with an air temperature of 90 F and a relative humidity of 50%.  We'll figure out the mixing ratio and the dew point temperature.  The problem is worked out in detail below:


First you fill in the air temperature and the RH data that you are given.

(A) since you know the air's temperature you can look up the saturation mixing ratio (30 g/kg). 

(B)  Then you might be able to figure out the mixing ratio in your head.  Air that is filled to 50% of its capacity could hold up to 30 g/kg.  Half of 30 is 15, that is the mixing ratio.  Or you can substitute into the relative humidity formula and solve for the mixing ratio (the details are shown above).


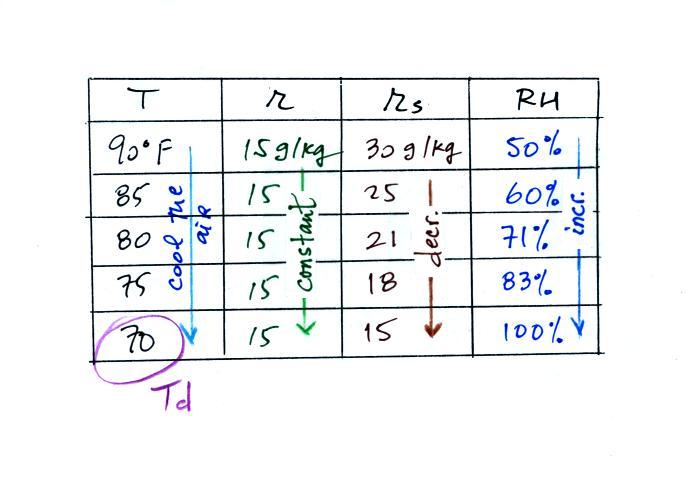
Finally, to determine the dew point, we imagine cooling the air.  The saturation mixing ratio decreases, the mixing ratio stays constant, and the relative humidity increases.   In this example the RH reachs 100% when the air has cooled to 70 F.  That is the dew point temperature.

We can use results from humidity problems #1 and #2 to learn a useful rule.


In the first example the difference between the air and dew point temperatures was large (45 F) and the RH was low (20%).  In the 2nd problem the difference between the air and dew point temperatures was smaller (20 F) and the RH was higher (50%).  The easiest way to remember this rule is to remember the case where there is no difference between the air and dew point temperatures.  The RH then would be 100%.
Example 3
In this problem we're given a mixing ratio of 10.5 g/kg and a relative humidity of 50%.  What are the air's temperature and the dew point temperature?
Here's the play by play solution to the question


(1) The air contains 10.5 g/kg of water vapor, this is 50%, half, of what the air could potentially hold.  So the air's capacity, the saturation mixing ratio must be 21 g/kg (you can either do this in your head or use the RH equation following the steps shown). 

(2) Once you know the saturation mixing ratio you can look up the air temperature in a table (80 F air has a saturation mixing ratio of 21)

(3) Then you imagine cooling the air until the RH becomes 100%.  This occurs at 60 F.  The dew point is 60 F.
Example 4
This probably the most difficult problem of the bunch.  We're given the air temperature (90 F) and the dew point temperature (50 F) and asked to figure out the mixing ratio and the relative humidity.


We enter the two temperatures onto a chart and look up the saturation mixing ratio for each.

We ignore the fact that we don't know the mixing ratio.  We do know that if we cool the 90 F air to 50 F the RH will become 100%.  We can set the mixing ratio equal to the value of the saturation mixing ratio at 50 F, 7.5 g/kg.


Remember back to the three earlier examples.  When we cooled air to the the dew point, the mixing ratio didn't change.  So the mixing ratio must have been 7.5 all along.   Once we know the mixing ratio in the 90 F air it is a simple matter to calculate the relative humidity, 25%.

Here's a summary of some of the important facts and properties of the 4 humidity variables that we have been talking about. 




Now we can start to use what we have learned about humidity variables (what they tell you about the air and what causes them to change value) to learn some new things. 



At Point 1 we start with some 90 F air with a relative humidity of 25%, fairly dry air (these data are the same as in Problem #4 above).  Point 2 shows the air being cooled to the dew point, that is where the relative humidity would reach 100% and a cloud would form.    Then the air is cooled below the dew point, to 30 F.  Point 3 shows the 30 F air can't hold the 7.5 g/kg of water vapor that was originally found in the air.  The excess moisture must condense (we will assume it falls out of the air as rain or snow).  When air reaches 30 F it contains 3 g/kg, less than half the moisture that it originally did (7.5 g/kg).  Next, Point 4, the 30 F air is warmed back to 90 F, the starting temperature, Point 5.  The air now has a RH of only 10%.

Drying moist air is like wringing moisture from a wet sponge. 


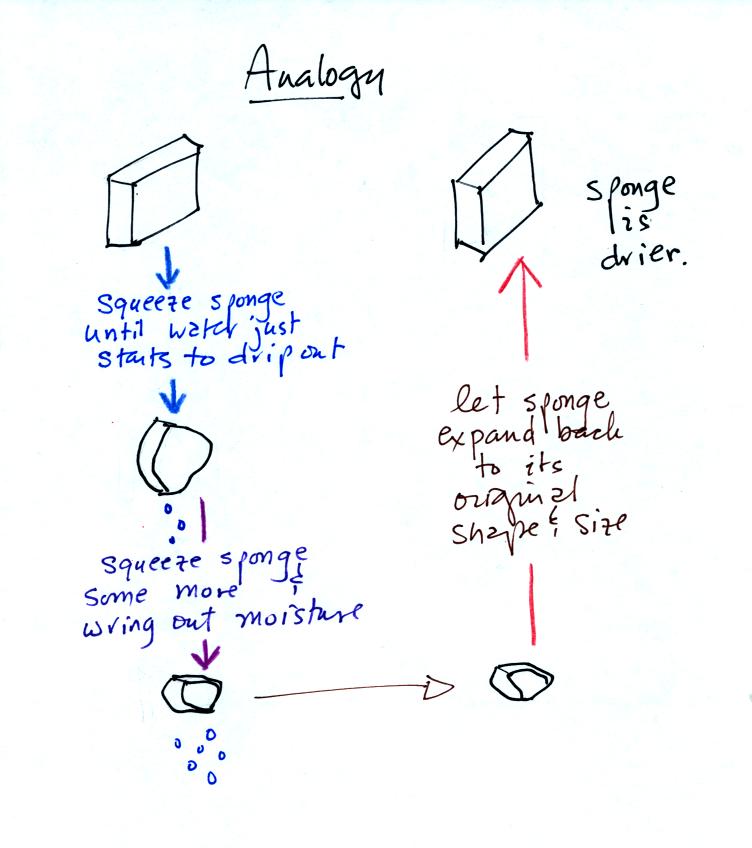
You start to squeeze the sponge and nothing happens at first (that's like cooling the air, the mixing ratio stays constant as long as the air doesn't lose any water vapor).  Eventually water will start to drop from the sponge (with air this is what happens when you reach the dew point and continue to cool the air below the dew point).  Then you let go of the sponge and let it expand back to its orignal shape and size (the air warms back to its original temperature).  The sponge (and the air) will be drier than when you started.

This sort of process ("squeezing" water vapor out of moist air by cooling the air below its dew point) happens all the time.  Here are a couple of examples.

In the winter cold air is brought inside your house or apartment and warmed.  Imagine 30 F air with a RH of 100% (this is a best case scenario, the cold winter air usually has a lower dew point and is drier). Bringing the air inside and warming it will cause the RH to drop from 100% to 20%..  Air indoors during the winter often has a very low relative humidity.

The air in an airplane comes from outside the plane.  The air outside the plane can be very cold (-60 F perhaps) and contains very little water vapor (even if the -60 F air is saturated it would contain essentially no water vapor).  When brought inside and  warmed to a comfortable temperature, the RH of the air in the plane will be very close 0%.  Passengers often complain of becoming dehydrated on long airplane flights.  The plane's ventilation system probably adds moisture to the air so that it doesn't too dry.

Here's a very important example, the rain shadow effect. 



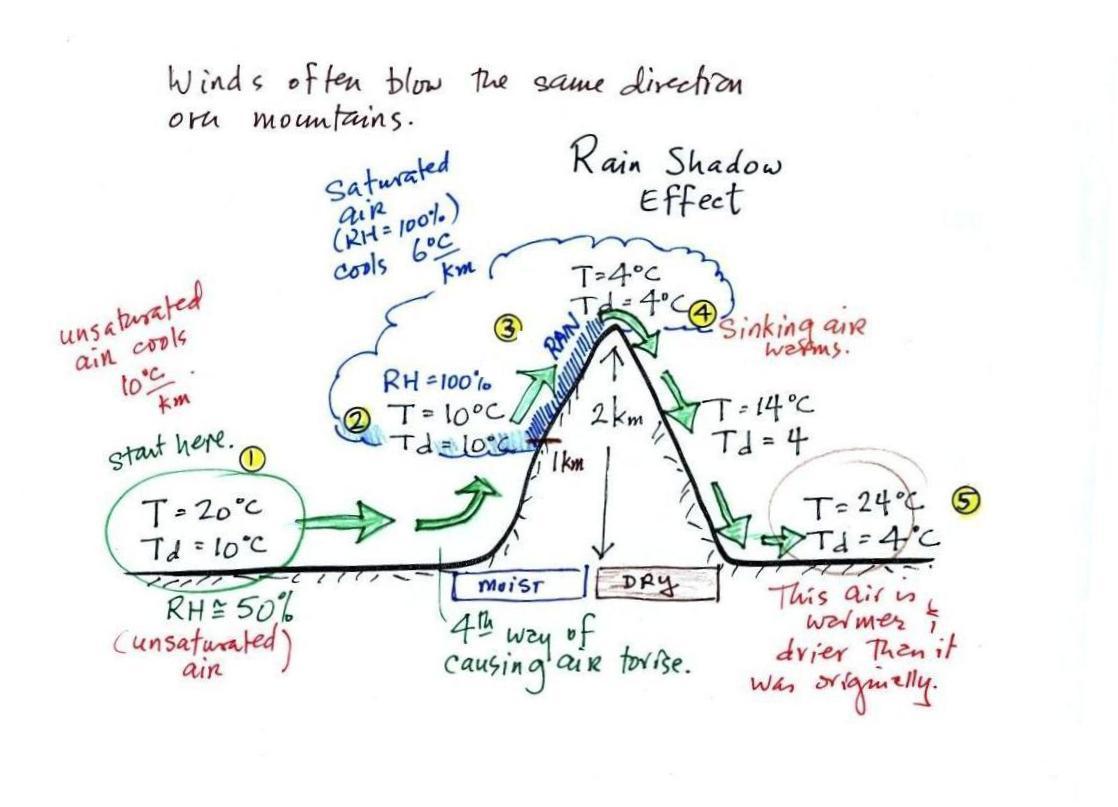
We start with some moist but unsaturated air (RH is about 50%) at Point 1.  As it is moving toward the right the air runs into a mountain and starts to rise (see the note below).  Rising air expands and cools.   Unsaturated air cools 10 C for every kilometer of altitude gain.  This is known as the dry adiabatic lapse rate and isn't something you need to remember at this point.  So in rising 1 km the air will cool to 10 C which is the dew point.

The air becomes saturated at Point 2, you would see a cloud appear.  Rising saturated air cools at a slower rate than unsaturated air (condensation of water vapor releases latent heat energy, this warming partly offsets the cooling caused by expansion).  We'll use a value of 6 C/km (an average value).  The air cools from 10 C to 4 C in next kilometer up to the top of the mountain.  Because the air is being cooled below its dew point at Point 3, some of the water vapor will condense and fall to the ground as rain.  Moisture is being removed from the air.

At Point 4 the air starts back down the right side of the mountain.  Sinking air is compressed and warms.  As soon as the air starts to sink and warm, the relative humidity drops below 100% and the cloud disappears.  The sinking unsaturated air will warm at the 10 C/km rate. 

At Point 5 the air ends up warmer (24 C vs 20 C) and drier (Td = 4 C vs Td = 10 C) than when it started out.  The downwind side of the mountain is referred to as a "rain shadow" because rain is less likely there than on the upwind side of the mountain.  Rain is less likely because the air is sinking and because the air on the downwind side is drier than it was on the upslope side.

Most of the year the air that arrives in Arizona comes from the Pacific Ocean.  It usually isn't very moist by the time it reaches Arizona because it has travelled up and over the Sierra Nevada mountains in California and the Sierra Madre mountains further south in Mexico.  The air loses much of its moisture on the western slopes of those mountains.  The eastern half of Oregon is drier than the western half because air travels from the Pacific up and over the Cascade mountains.  It loses a lot of its moisture on the upslope side of the mountains.

Note:  This figure illustrates orographic lifting.  It is a 4th way of causing rising air motions (convergence into surface low pressure centers, fronts, and free convection are the others).  Rising air is important because rising air expands and cools.  If the air is cooled enough clouds can form.