The first step is to realize that warm water will evaporate more rapidly than cool water. You probably know that already. If a cup of iced tea were set next to a cup of hot tea you probably be able to tell which was which by just looking at them. You wouldn't need to touch the cups or taste the tea or look for ice cubes.
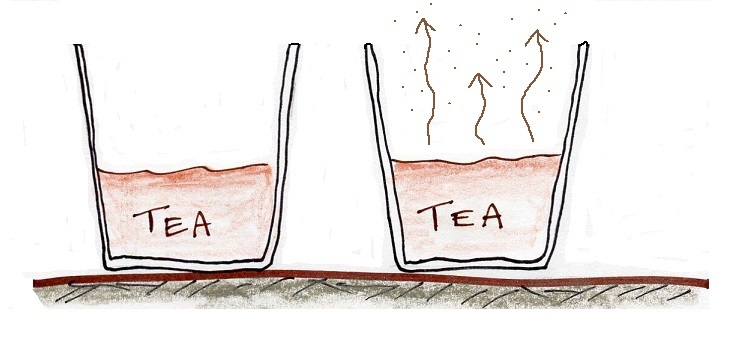
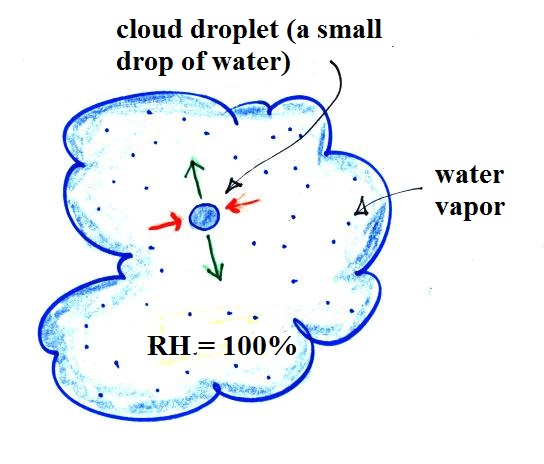
You would probably notice that one of the cups of tea was steaming (the cup on the right above). That would be the hot tea. The steam that you see is not actually water vapor. Rather water vapor is evaporating so quickly that it is filling the cooler air above with more moisture than it can handle (the relative humidity is over 100%, the air is supersaturated with moisture). The excess water vapor condenses (bringing the relative humidity down to 100%) and forms a faint cloud of very small drops of water. That's what you are seeing.
Next we'll pour out the tea and fill a cup with some room temperature water and let it sit on a table for a day or two.
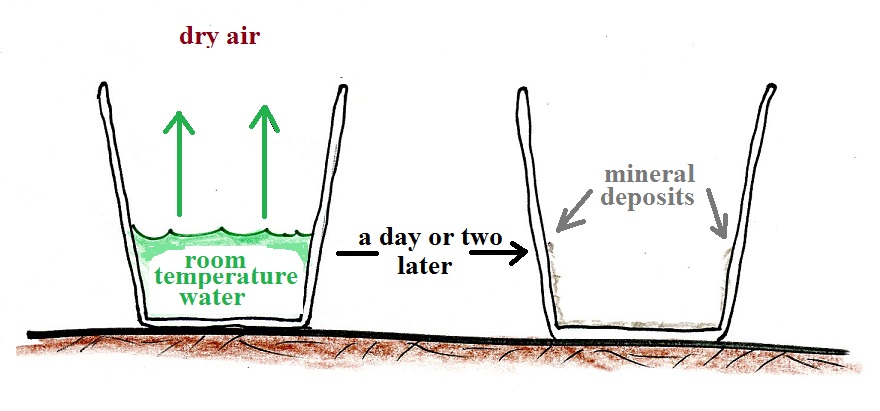
That doesn't happen if we put a cover on the cup.
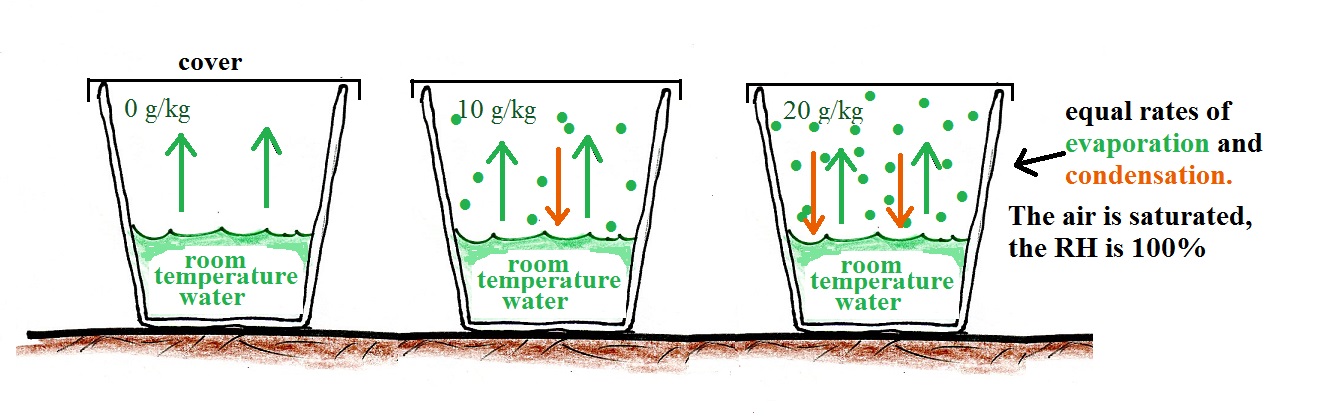
The cover keeps the water vapor is kept inside the cup. As the amount of water vapor begins to build up inside the cup some of that water vapor will condense (even though it might just have evaporated).
Here's the second key point. The rate of condensation will depend on how much water vapor is in the air. As the water vapor concentration builds, the rate of condensation will increase. Eventually the amount of water will increase to the point where the rate of condensation will equal the rate of evaporation. That's a balanced equilibrium situation. The water vapor concentration won't increase beyond that point. The air has now become saturated with water vapor and the relative humidity (RH) is 100%.
What if we uncovered the cup and added a bunch more water vapor, enough to raise the RH over 100%?
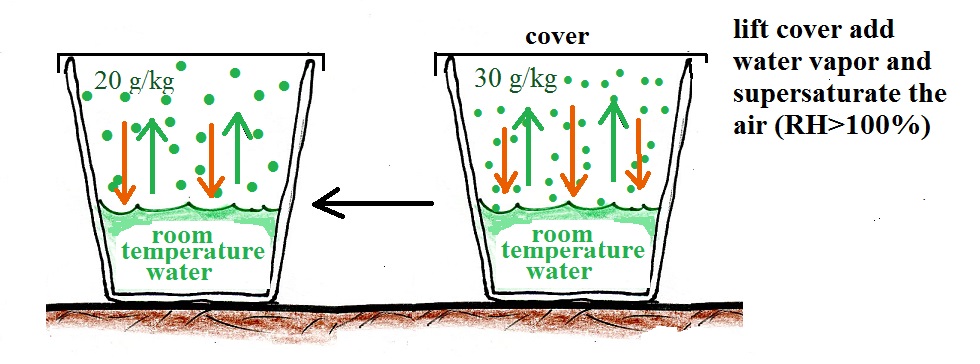
The greater amount of water vapor will increase the rate of condensation. The rate of condensation will for a time exceed the rate of evaporation. This is an imbalance. More water vapor is being removed from the air than is being added. The amount of water vapor in the air will decrease which will lower the rate of condensation. Eventually everything will be back in balance again.
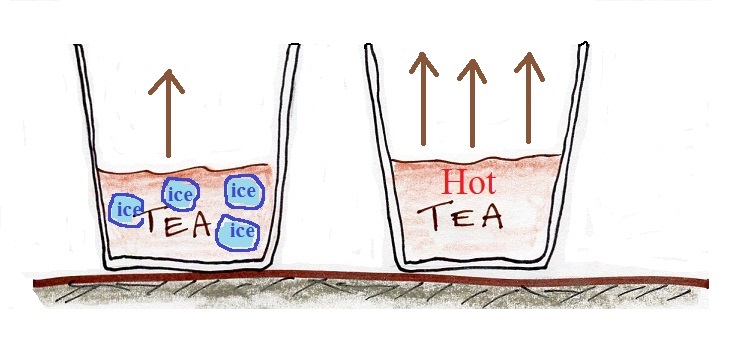
In the example above we considered room temperature water. In the figure below we compare glasses filled with cold water, room temperature water, and warm water. The air is saturated, the RH is 100%, in all three cases.
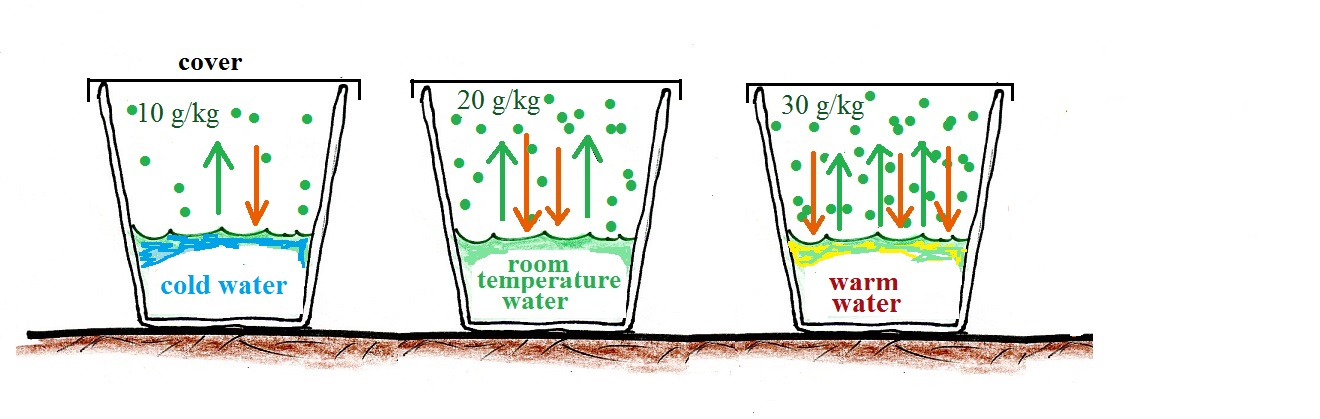
The rate of evaporation increases with increasing temperature. This requires higher and higher rates of condensation to balance the rate of evaporation. Higher and higher rates of condensation means increasing amounts of water vapor in the air. The RH is 100% and the air is saturated in each case above.
An Optional Assignment
Here's something to test your understanding of this material. Turn in correct answers to at least three of the four questions below by the start of class next Monday (Mar. 28) and I'll give you a Green Card that you can use on the next quiz.
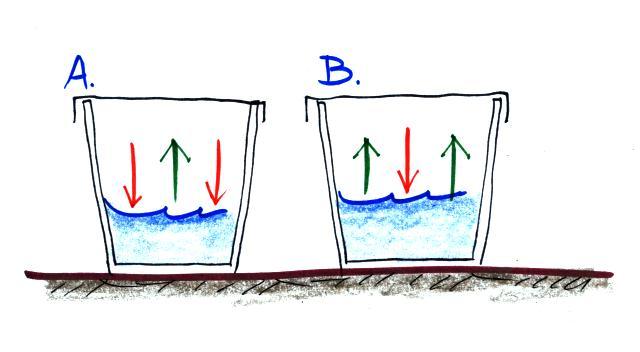
Here are the 4 questions:
(i) Is the water in Glass A WARMER or COLDER than in Glass B? (use the arrows, not the color of the water, to answer this question)
(ii) Is there MORE or LESS water vapor in the air in Glass A than in Glass B?
(iii) Is the relative humidity in each glass MORE than 100%, LESS than 100% or is it EQUAL to 100%.
(iv) The rates of evaporation and condensation aren't equal in either glass, so the pictures will change with time. What will the glasses look once they have reached equilibrium? (hint: will the amount of water vapor in the air in each case increase or decrease, how will that affect the rate of condensation)
Click here for the answers to the questions above.