Mon., Apr. 10 notes

Mon., Apr. 10, 2006

Reports turned in last week have been graded and were returned in class. The in-class optional assignment turned in last Friday has also been graded (every problem was graded) and was returned. You can still turn in this assignment on or before the beginning of class on Wednesday for partial credit.

A quick review of some of what we covered last Friday. The pressure gradient force (PGF) is one of the forces that causes the wind to blow. The PGF always points in a direction that is perpendicular to the contours on a weather map and toward low. The strength of the PGF depends on the spacing of the contour lines: the PGF is strong when the contours are close together and weak when they are far apart.

Upper level winds (horizontal winds) in the atmosphere are determined by only two forces the PGF and the Coriolis force (CF). We started to go over the Coriolis force on Friday but ran out of time. We went over it again today.

The figure above is from p. 122c in the photocopied notes. Imagine that a flying saucer flies over Tucson. It travels straight from west to east. The next figure shows the path that the saucer followed as it passed over the city.

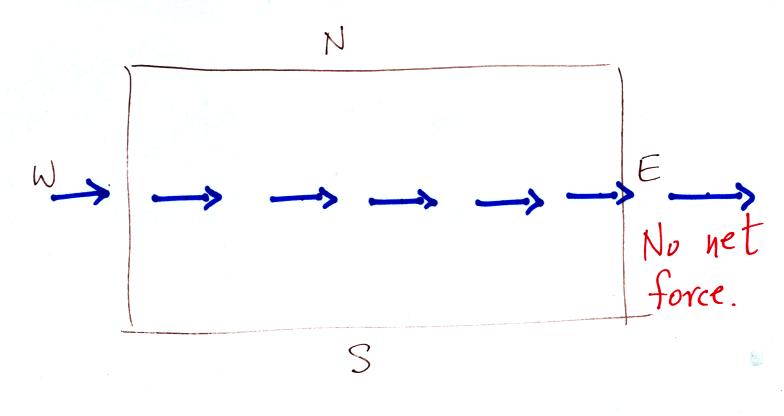
The flying saucer appeared (relative to the ground) to be moving in a straight line at constant speed. You would conclude that there was zero net force acting on the flying saucer.

In this second picture the flying saucer flies by overhead just as it did in the previous picture. In this picture, however, the ground is moving (don't worry about what might be causing the ground to move).

This is the path that you would see relative to the ground in this case. Even though the flying saucer flew from west to east it appears to have been traveling from the NW toward the SE because the ground was moving as the flying saucer passed overhead. Because the motion is still in a straight line at constant speed, you would conclude the net force acting on the flying saucer was zero.

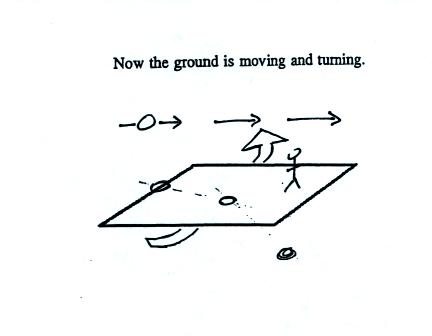
In this last figure the flying saucer flies by again from west to east. In this case however the ground is rotating.

Now the flying saucer appears to have been turning to the right as it passed over Tucson. Because it is no longer traveling in a straight line you would conclude there was a net force acting on the flying saucer. The direction of this net force would be to the right of the motion.

At most locations on the earth the ground is rotating. This is most easily seen at the poles.

Imagine a piece of paper glued to the top of a globe. As the globe spins the piece of paper will rotate. A piece of paper glued to the globe at the equator won't spin, it will flip over. At points in between the paper would spin and flip, the motion gets complicated.

The easiest thing for us to do is to ignore the fact that the ground on which we are standing is rotating. However, if we do that we need to account for the curved paths that moving objects will take when they move relative to the earth's surface. That is what the Coriolis force does.
\

Here are some rules that you can use to determine the direction and strength of the Coriolis force. It always points in a direction that is perpendicular to the wind, it can't cause the wind to speed up or slow down, it will only change the wind's direction.

The red arrows show the direction of the CF in the northern and southern hemispheres. The CF is to the right of the wind (you need to look in the direction the wind is blowing, you need to look downstream) in the northern hemisphere and to the left of the wind in the southern hemisphere. This figure and the next 2 figures were on a class handout distributed in class.

As we saw last Friday, the PGF is the only force that can cause stationary air to begin to move.

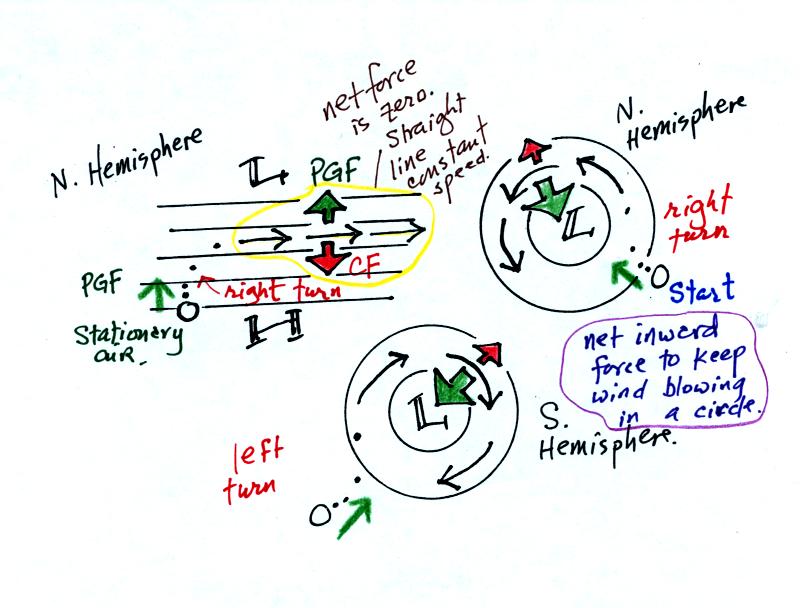
Once the wind begins to move the Coriolis force can cause it to turn to the right or left.

Air in the upper left figure begins to move toward the Low at the top of the figure. The CF then turns the wind to the right (this tells you this is a northern hemisphere map). The wind ends up blowing parallel to the contour lines. When the contour lines are straight, the wind will blow in a straight line at constant speed. The net force will be zero, the PGF and CF point in equal directions and have the same strength. They cancel each other out.

Winds will spin counterclockwise around low in the northern hemisphere and clockwise around lows in the southern hemisphere. The winds blow parallel to the circular contour lines. A net inward force must be present in order for the wind to be able to blow in a circular path like this. In these two low pressure center examples, the inward PGF is a little stronger than the outward pointing CF.

The back page of the class handout had a bunch of other examples that you can study and turn in at the beginning of class on Wednesday as an optional assignment.

Now we will briefly look at surface winds.

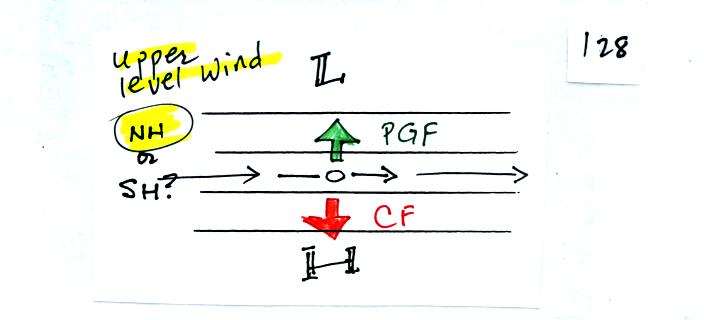
This figure shows upper level winds. You only need to worry about two forces: PGF and CF.

Now we add the frictional force. Friction will always try to slow down a moving object. The strength of the frictional force depends on speed. If the wind isn't blowing at all (speed is zero), the frictional force is also zero.

The effect of friction is to slow down surface winds and to cause them to blow across the contour lines toward Low. In the example above the PGF is balanced by the Friction and CF working together. The net force is zero, the wind will blow in a straight line at constant speed across the contour lines as shown.

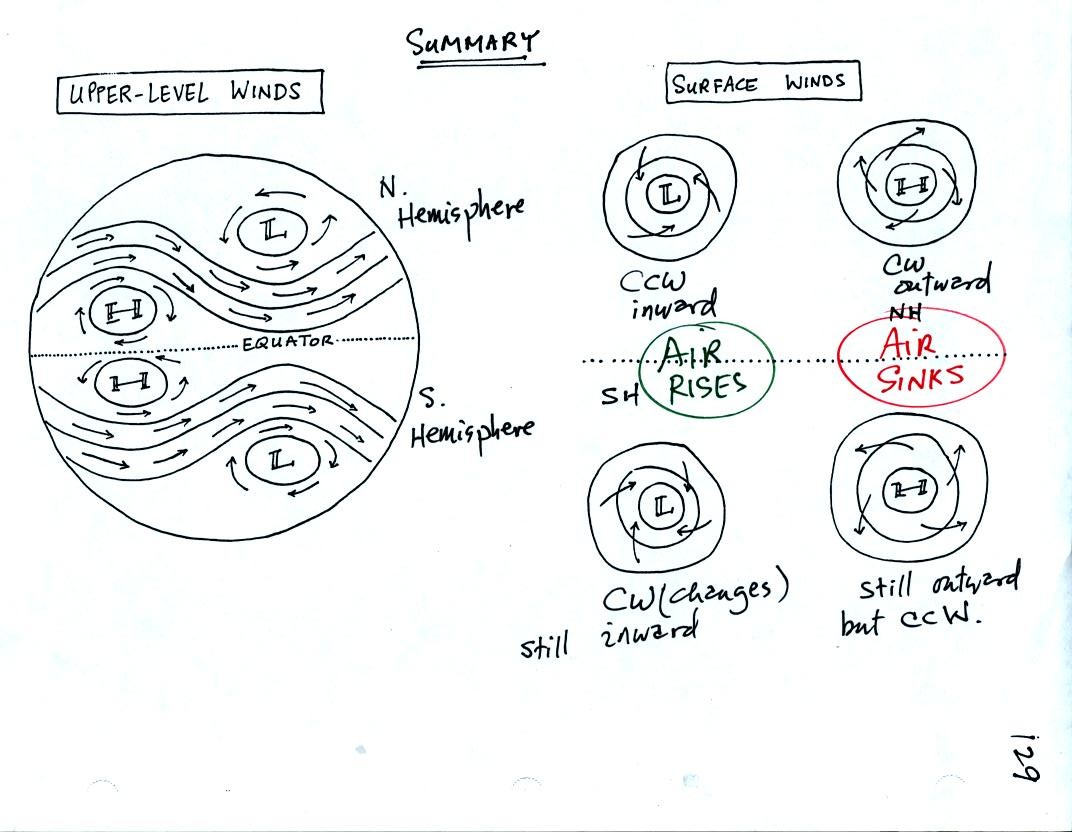
This figure shows upper level winds at left and the surface winds that blow around centers of high and low pressure at right. Note winds spin counterclockwise (CCW) around lows in the northern hemishere and clockwise (CW) around lows in the southern hemisphere. Surface winds converge (blow in) toward centers of Low pressure in both hemispheres. This convergence causes rising air motions. Thus you would expect to see clouds associated with low pressure in both hemispheres..