Friday, Feb. 24, 2006

A new optional assignment was distributed in class.  It is due next Friday, March 3.

The Expt. 1 revised reports and the Expt. 2 reports are due next Monday.  1S1P Assignment #2 is due next Wednesday.
reules governing the emission of EM radiation
Unless an object is very cold (0 K) it will emit EM radiation.  All the people, the furniture, the walls and the floor in the classroom are emitting EM radiation.  Often this radiation will be invisible so that we can't see it and weak enough that we can't feel it.  Both the amount and kind (wavelength) of the emitted radiation depend on the object's temperature.

The Stefan Boltzmann law allows you to determine the amount of energy emitted per unit area per second (calories emitted per square centimeter per second for example).  Don't about the units.  Don't worry about σ either, it is just a constant.  The Stefan Boltzmann law tells you the amount or the intensity or the rate at which energy is emitted by an object.  The amount depends on temperature to the fourth power.  If the temperature of an object doubles the amount of energy emitted will increase by a factor of 2 to the 4th power (2x2x2x2=16).  A hot object just doesn't emit more energy than a cold object it emits a lot more energy than a cold object.

Objects usually don't just emit a single wavelength of EM radiation.  Rather they emit a wide range of wavelengths.  This is illustrated on the graph at the bottom of the page above.  There is a wavelength at which the object emits more radiation than at other wavelengths.  This is λmax  "lambda max."  Wien's law allows you to calculate the value of λmax.  If you divide 3000 by the temperature of the object (in K) you will obtain λmax in micrometers.

The area under the curves is the total energy emitted by an object. The area under the "Hot" object's curve is much larger than the area under the "Cold" object's curve.  Notice that λmax  for the hot object has shifted to shorter wavelength.

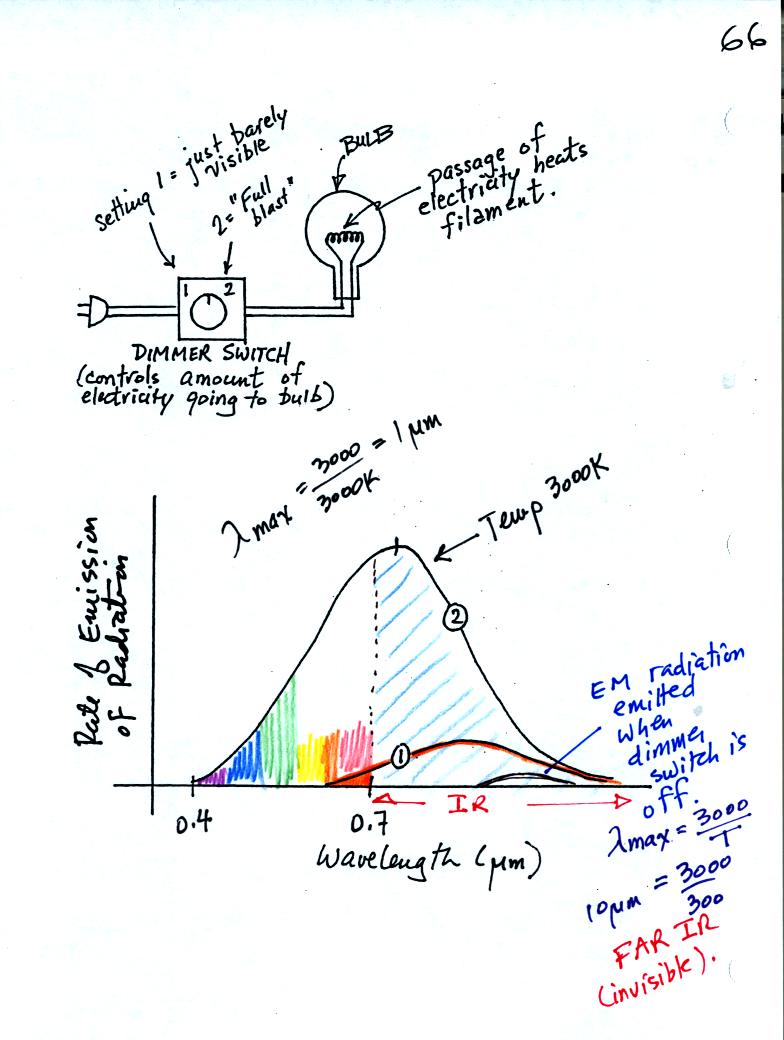
radiation emitted by a tungsten lightbulb
We can use a light bulb connected to a dimmer switch to demonstrate Stefan Boltzmann and Wien's laws. 

First with the electricity turned off, the bulb filament will have a temperature of about 300 K, about room temperature. You might be able to just make out the small curve at the bottom right corner of the graph showing the EM radiation emitted by the bulb.  λmax is about 10 μm.  That is invisible infrared radiation you wouldn't see any light coming from the bulb.  The area under the curve is very small, the bulb isn't emitting much energy.

Next we turn on the dimmer switch until the bulb filament just begins to glow (with an orangish color).  This is curve 1 on the graph above.  The bulb isn't producing much visible light, just a little bit of red and orange light.  Most of the light produced by the bulb lies to the right of 0.7 μm.  That means it is IR radiation. The area under  Curve 1 is relatively small, the bulb isn't emitting very much energy.

Finally we turn the dimmer switch completely on.  The bulb got very bright (it was a 200 Watt bulb).  The filament is much hotter now and emits a lot more energy than it did.  That is the Stefan Boltzmann law in action.  About 40% of Curve 2 in the figure above, representing the EM radiation now being emitted by the bulb, now lies to the left of 0.7 μm and is visible light.  Because it is a mixture of all the colors it appears white (it is a "warm" white meaning it contains more red and orange light than it does violet and blue).  A tungsten bulb like this has a temperature of about 3000K meaning λmax is about 1 μm, still invisible IR radiation.  A tungsten bulb is not an especially efficient producer of visible light, more than half the light produced by the bulb is invisible.

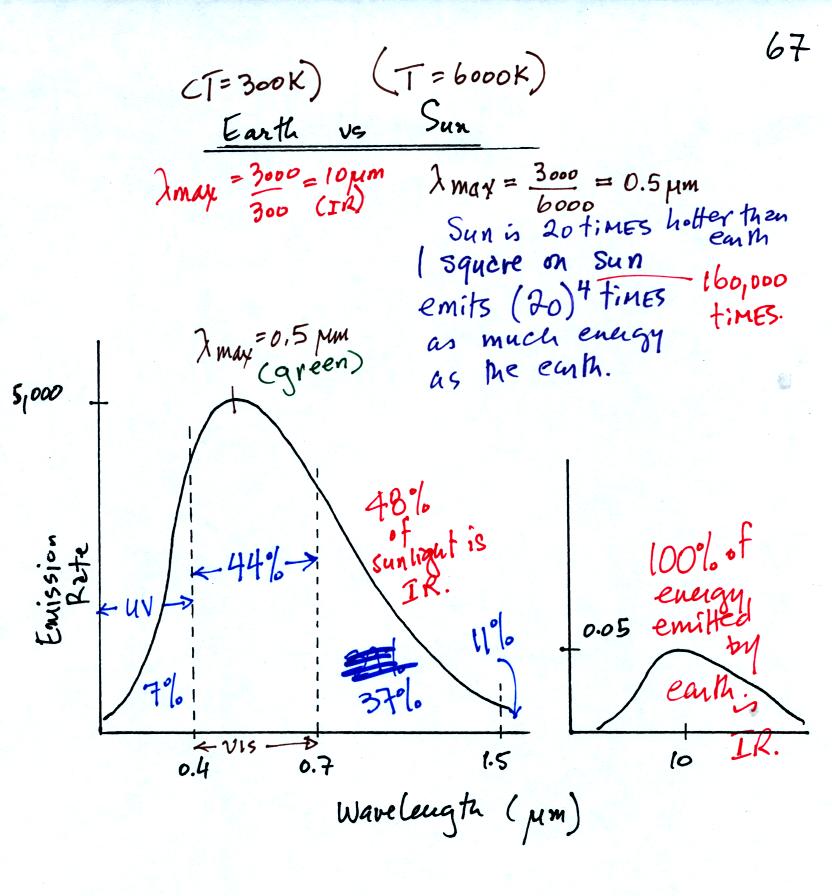
EM radiation emitted by the earth and sun

The wavelength  of peak emission for the earth is about 10 μm, IR radiation.  Peak emission from the sun is 0.5μm, green light.  The sun emits other colors however in less amounts and the mixture appears white.  About 7% of the light emitted by the sun is UV light, 44% is visible light, and 48% is IR light.  The remaining 1% is emitted at longer wavelengths.  The surface of the sun is 20 times hotter than the earth so the sun emits energy at about 160,000 times the rate of the earth.

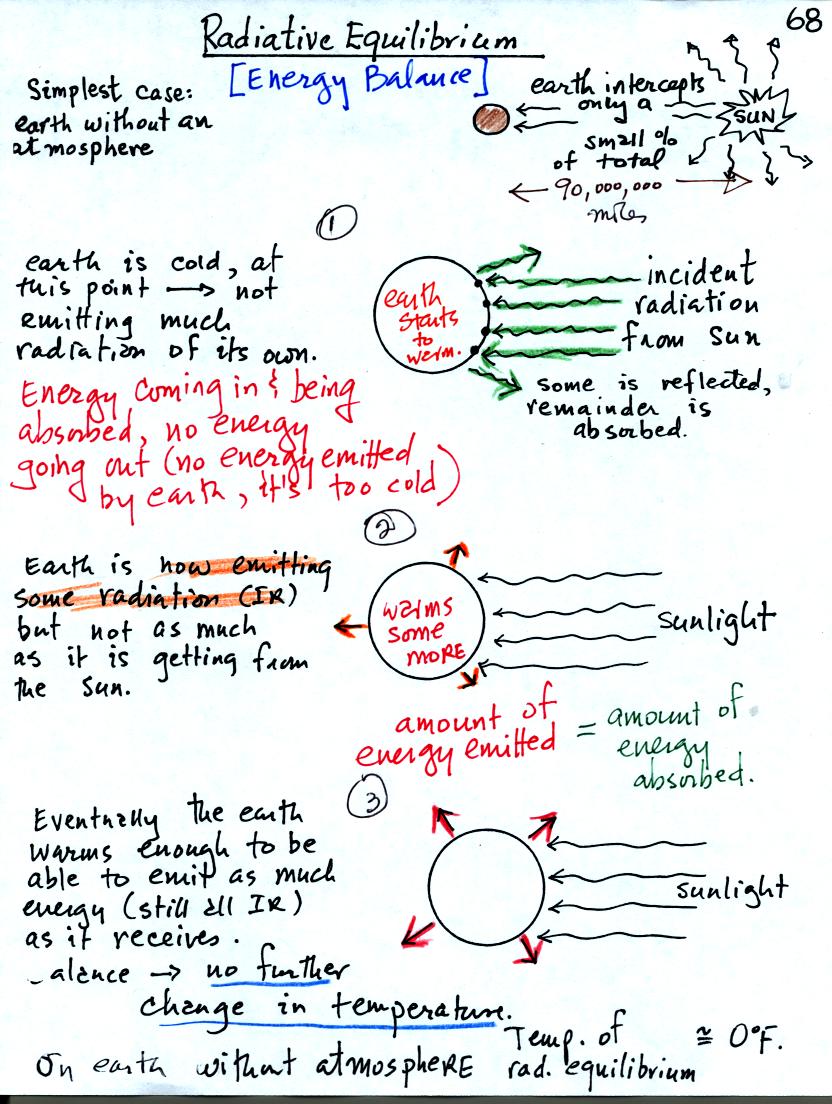
radiative equilibrium on the earth without an atmosphere

Energy balance on the earth without an atmosphere.  The earth starts out very cold and is not emitting any EM radiation.  It is absorbing sunlight however so it will warm.  Once the earth starts to warm it will begin to emit EM radiation, though not as much as it is getting from the sun.  Eventually it will warm enough that the earth will emit the same amount of energy (though not the same wavelength energy) as it absorbs from the sun.  This is radiative equilibrium.  The temperature at which this occurs is 0 F (on the earth without any atmosphere)

Click here for a look ahead to next Monday's class.