Thursday Feb. 23, 2006

A new optional assignment was distributed in class.  It is due next Thursday, March 2.

An online version of the Controls of Temperature topic covered in Chapter 3 is now available.  This is the only part of Chapter 3 that will be assigned.  The online version should cover the topic in sufficient detail that students buying chapters individually won't have to purchase Chapter 3.

The Expt. 1 revised reports and the Expt. 2 reports are due next Tuesday.  1S1P Assignment #2 is due next Thursday.

---

Energy transport by EM radiation is the most important of the 4 energy transport processes because it is capable of carrying energy through empty space; that is something the other three can't do.  We'll briefly review static electricity, learn something about electric fields, and then use these concepts to gain a little understanding of EM radiation.

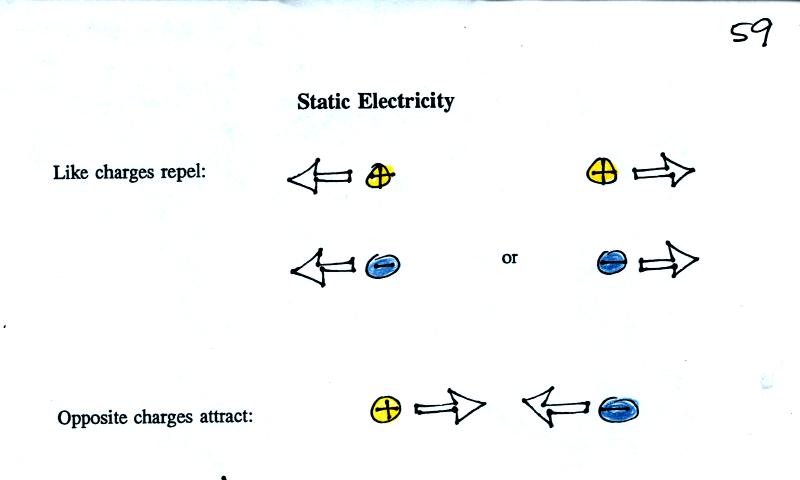
Two charges of the same polarity (like charges) would be pushed apart if they are placed near each other.  Two charges of opposite polarity would be attracted. The figure above and the one below can be found on p. 59 in the photocopied class notes.

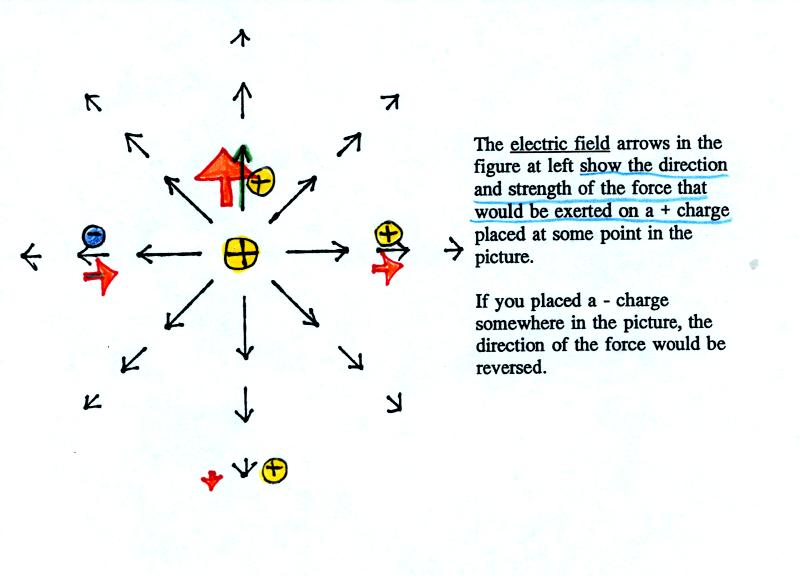
The figure above shows the pattern of electric field arrows around a central + charge.  The E field arrows show what would happen if a second + charge were placed somewhere in the picture.  Three + charges (in yellow) placed above, to the right, and below the center charge are all pushed outward and away from the center charge.  The outward force becomes weaker when the distance between the two charges increases.  A negative charge placed to the left of the center charge is attracted to the center positive charge.

Click here for some sample questions about electric fields and static electricity.

The figures on p. 60 in the photocopied have been broken into 3 parts below for clarity.

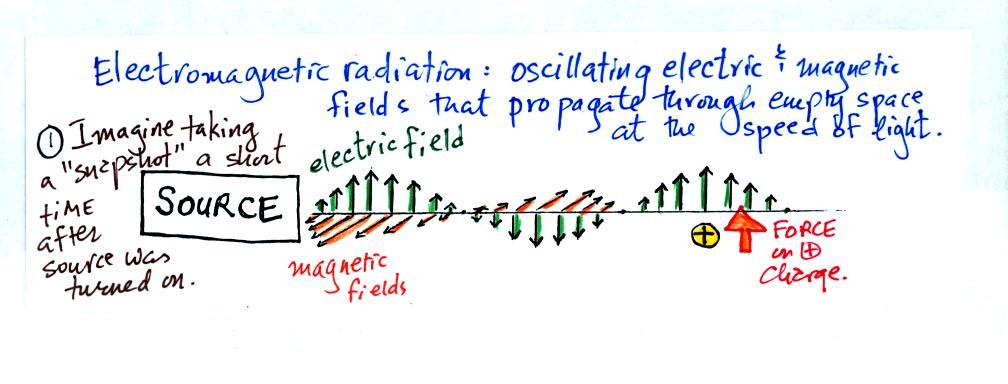
We imagine turning on a source of EM radiation and then a short time later we take a snapshot.  The EM radiation is a wavy pattern of electric and magnetic field arrows.  We'll ignore the magnetic field lines.  The E field lines sometimes point up, sometimes down.  The pattern of arrows repeats itself. 

Note the + charge near the right of the picture.  At the time this picture was taking the EM radiation exerts a fairly strong upward force on the + charge.

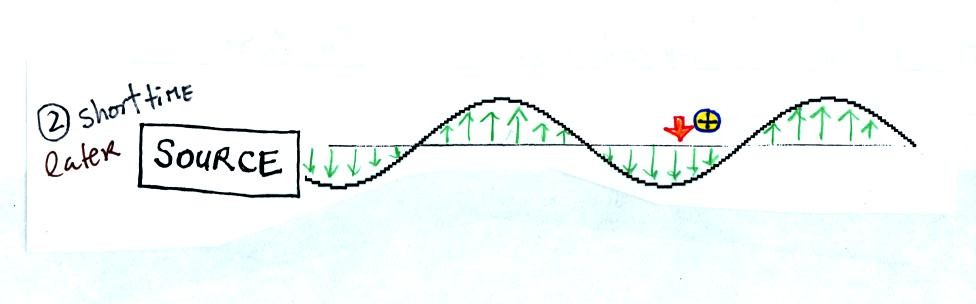
This picture was taken a short time later and the rediation has traveled a little further to the right.  The EM radiation now exerts a relatively weak downward force on the + charge.


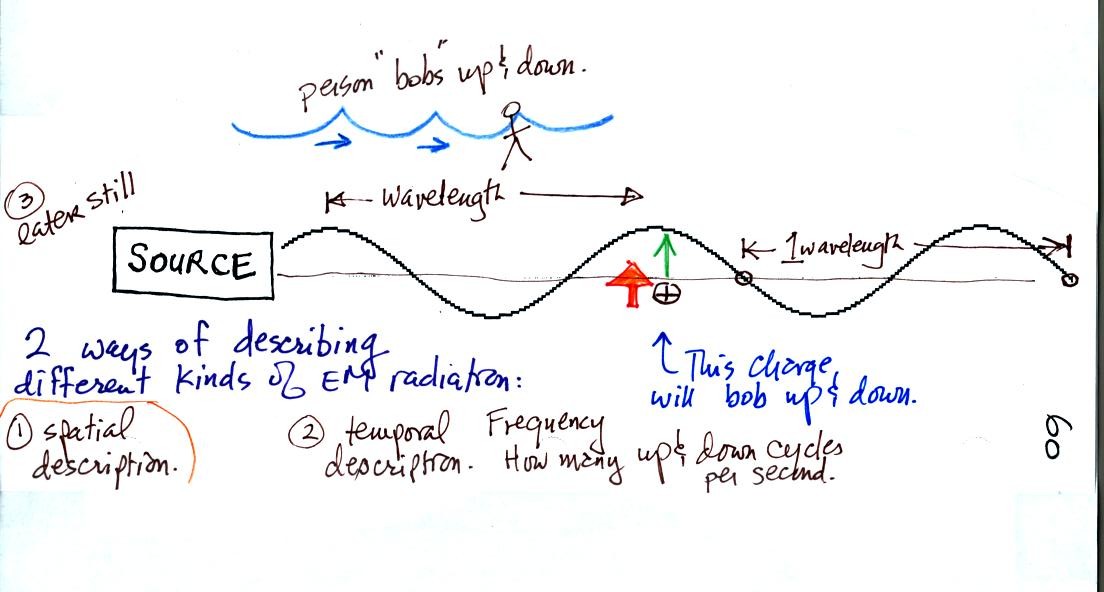
The + charge is now being pushed upward again.  A movie of the + charge would show it bobbing up and down much like a swimmer in the ocean would do as waves passed by.  The wavy pattern used to depict EM radiation (the wavy line connects the heads of the electric field arrows) can be described spatially in terms of its wavelength, the distance between identical points on the pattern.  Or you can describe the radiation temporally using the frequency of oscillation (number of up and down cycles completed by an oscillating charge per second)



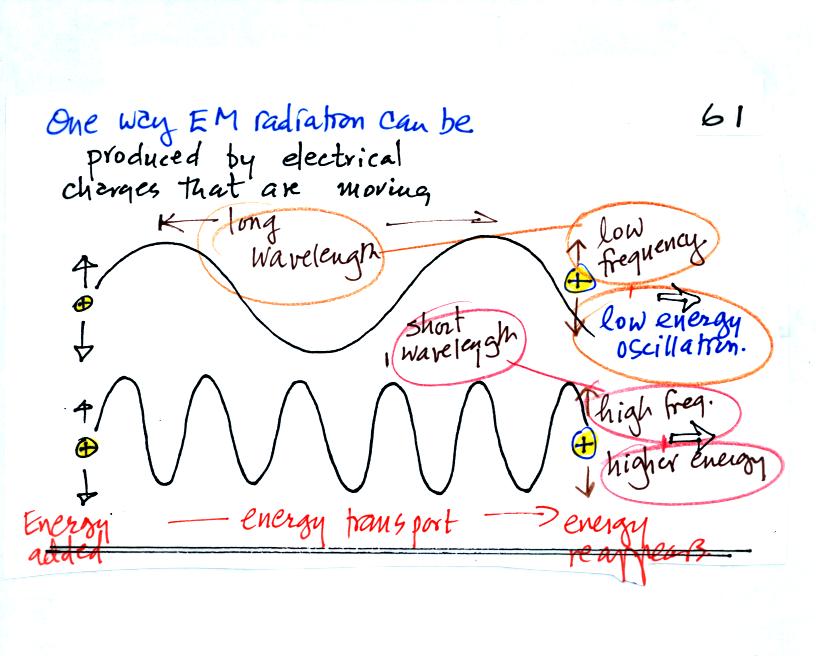
One way of producing is to cause electrical charge to move up and down.  You supply energy to cause the charge to oscillate and EM radiation is produced and propagates to the right.  The EM radiation encounters a charge somewhere else and causes it to begin to move up and down.  Energy has been transported to the charge.

Slow up and down oscillation produces long wavelength, low energy radiation.
Fast up and down oscillation produces shorter wavelength, higher energy radiation.

This relationship can be seen more clearly in the animation shown in class.  Use your mouse to move the slider to the left to lower the spring tension.  Then use the mouse to pull downward on the right hand charge.  It will begin oscillating slowly.  Long wavelength radiation will be produced that propagates to the left and causes the left hand charge to begin to oscillate at low frequency.  Moving the slider to the right will increase the spring tension.  Pulling down on the right hand charge will produce shorter wavelength radiation. 

Note the speed of progation (in empty space) of long and short wavelength radiation is the same.



Gamma rays, X-rays, and ultraviolet light are high-energy, short wavelength forms of EM radiation.  Infrared light, microwaves, and radio waves are longer wavelength, lower energy forms of radiation.

The different colors of visible light have wavelengths that range from 0.4 to 0.7 micrometers.  Mixing all the colors of visible light together produces white light.

---

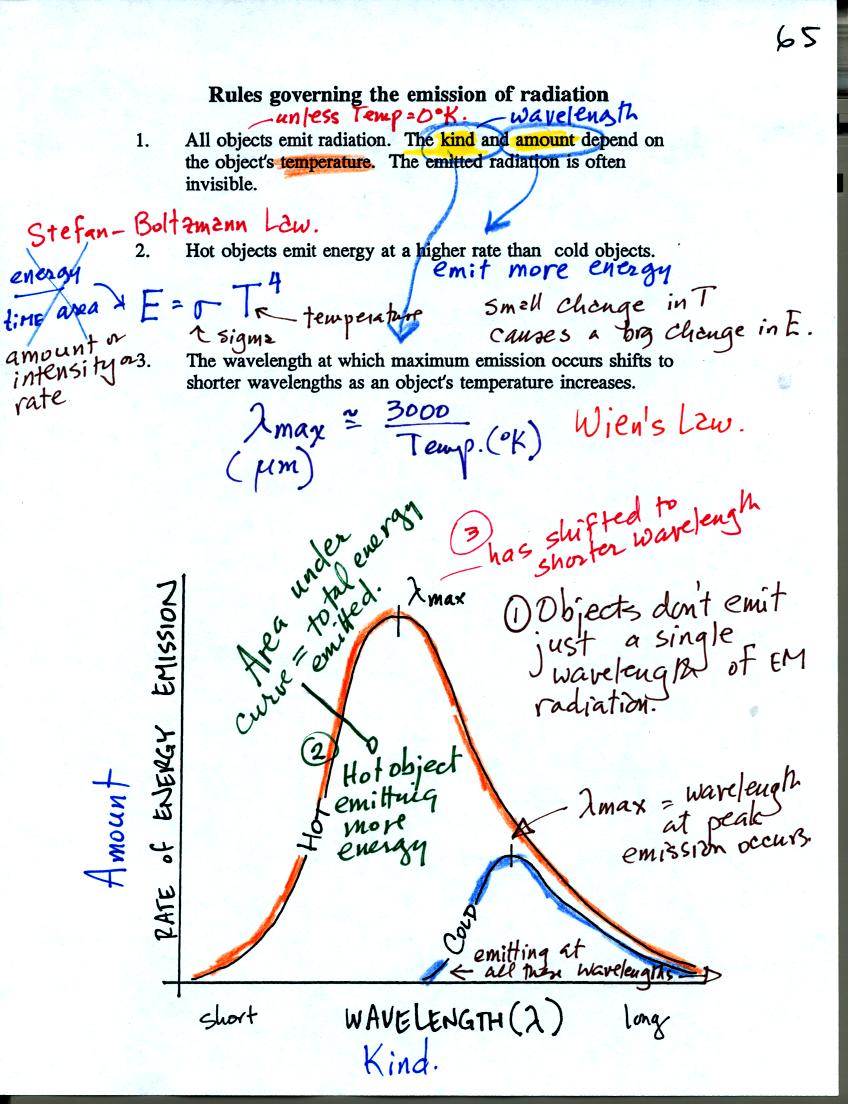
Unless an object is very cold (0 K) it will emit EM radiation.  All the people, the furniture, the walls and the floor in the classroom are emitting EM radiation.  Often this radiation will be invisible so that we can't see it and weak enough that we can't feel it.  Both the amount and kind (wavelength) of the emitted radiation depend on the object's temperature.

The Stefan Boltzmann law allows you to determine the amount of energy emitted per unit area per second (calories emitted per square centimeter per second for example).  Don't about the units.  Don't worry about σ either, it is just a constant.  The Stefan Boltzmann law tells you the amount or the intensity or the rate at which energy is emitted by an object.  The amount depends on temperature to the fourth power.  If the temperature of an object doubles the amount of energy emitted will increase by a factor of 2 to the 4th power (2x2x2x2=16).  A hot object just doesn't emit more energy than a cold object it emits a lot more energy than a cold object.

Objects usually don't just emit a single wavelength of EM radiation.  Rather they emit a wide range of wavelengths.  This is illustrated on the graph at the bottom of the page above.  There is a wavelength at which the object emits more radiation than at other wavelengths.  This is λmax  "lambda max."  Wien's law allows you to calculate the value of λmax.  If you divide 3000 by the temperature of the object (in K) you will obtain λmax in micrometers.

The area under the curves is the total energy emitted by an object. The area under the "Hot" object's curve is much larger than the area under the "Cold" object's curve.  Notice that λmax  for the hot object has shifted to shorter wavelength.


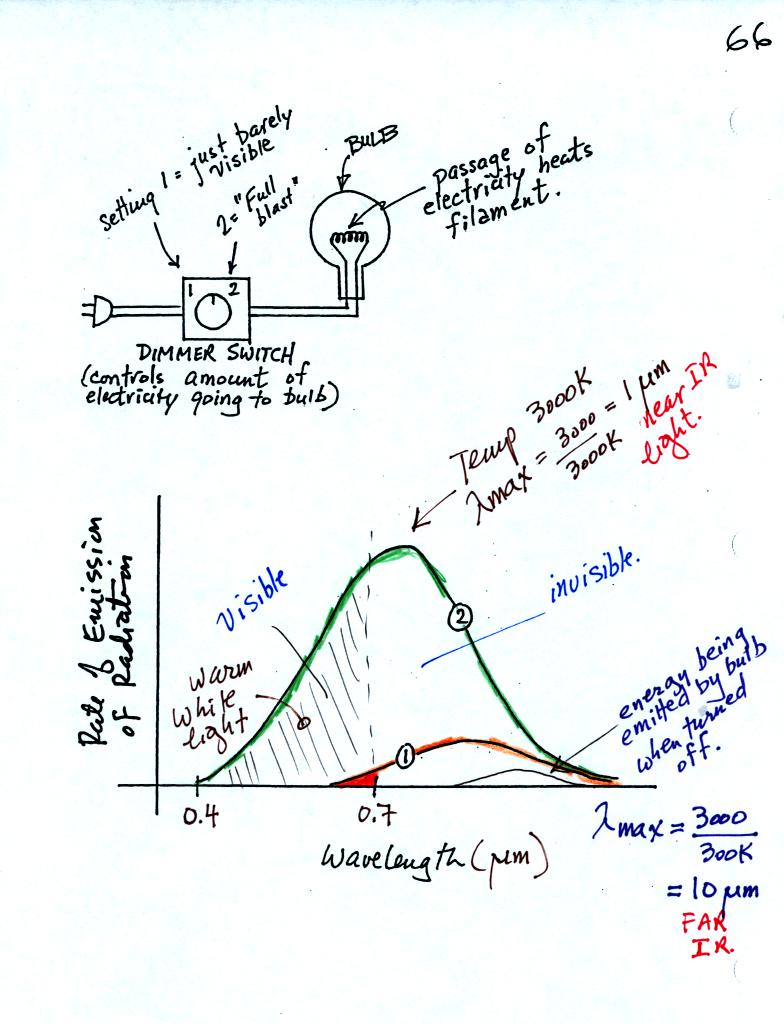
We can use a light bulb connected to a dimmer switch to demonstrate Stefan Boltzmann and Wien's laws. 

First with the electricity turned off, the bulb filament will have a temperature of about 300 K, about room temperature. You might be able to just make out the small curve at the bottom right corner of the graph showing the EM radiation emitted by the bulb.  λmax is about 10 μm.  That is invisible infrared radiation you wouldn't see any light coming from the bulb.  The area under the curve is very small, the bulb isn't emitting much energy.

Next we turn on the dimmer switch until the bulb filament just begins to glow (with an orangish color).  This is curve 1 on the graph above.  The bulb isn't producing much visible light, just a little bit of red and orange light.  Most of the light produced by the bulb lies to the right of 0.7 μm.  That means it is IR radiation. The area under  Curve 1 is relatively small, the bulb isn't emitting very much energy.

Finally we turn the dimmer switch completely on.  The bulb got very bright (it was a 200 Watt bulb).  The filament is much hotter now and emits a lot more energy than it did.  That is the Stefan Boltzmann law in action.  About 40% of Curve 2 in the figure above, representing the EM radiation now being emitted by the bulb, now lies to the left of 0.7 μm and is visible light.  Because it is a mixture of all the colors it appears white (it is a "warm" white meaning it contains more red and orange light than it does violet and blue).  A tungsten bulb like this has a temperature of about 3000K meaning λmax is about 1 μm, still invisible IR radiation.  A tungsten bulb is not an especially efficient producer of visible light, more than half the light produced by the bulb is invisible.




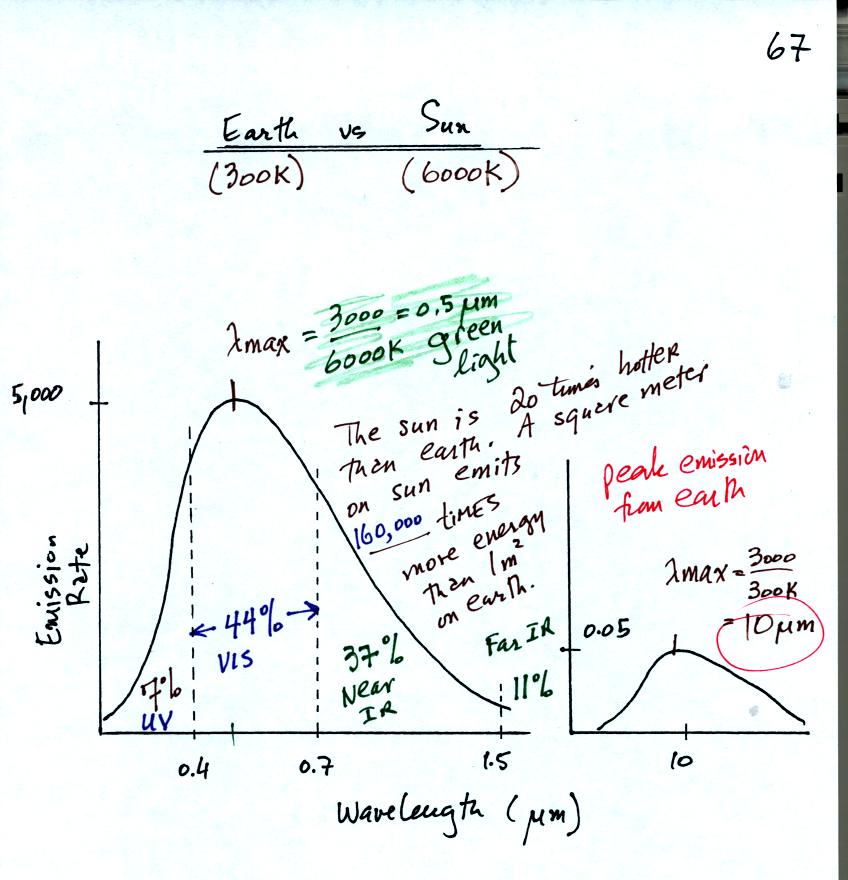
The wavelength  of peak emission for the earth is about 10 μm, IR radiation.  Peak emission from the sun is 0.5μm, green light.  The sun emits other colors however in less amounts and the mixture appears white.  About 7% of the light emitted by the sun is UV light, 44% is visible light, and 48% is IR light.  The remaining 1% is emitted at longer wavelengths.  The surface of the sun is 20 times hotter than the earth so the sun emits energy at about 160,000 times the rate of the earth.