Fri., Apr. 6 notes

Friday Apr. 6, 2007

The quiz papers were returned in class today.

An in-class optional assignment was distributed in class. The assignment will be collected at the beginning of class on Monday.

The notes below were hurriedly put together Friday afternoon and haven't yet been carefully proofread.

We'll spend about a week in Chapter 6 learning about the forces that cause surface and upper level winds.

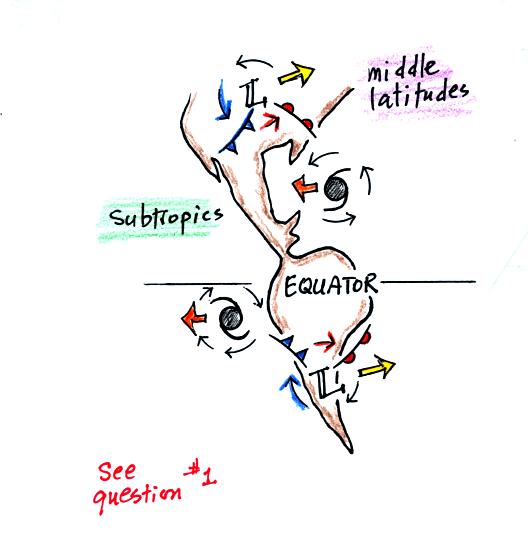
You can't leave NATS 101 Intro. to Weather and Climate without having been introduced to the Coriolis Force. It is part of the reason why winds spin counterclockwise (CCW) around Low pressure and clockwise (CW) around High pressure in the northern hemisphere. It is also causes winds to spin in the opposite directions around Highs and Lows in the southern hemisphere.

You may already have been to the southern hemisphere or you may go there one day (see Question #11 on the In-class Optional Assignment). You'll probably hear about how the Coriolis force or the Coriolis effect causes water to spin in a different direction in the southern hemisphere when it is draining out of a sink and toilet bowl (it's not true). That's another reason for covering the Coriolis effect in NATS 101.

Before learning about some of the other forces that cause or affect the wind we need to review Newton's Laws of Motion.

The 1st law really has two parts: one that deals with stationary objects and another part that treats moving objects.

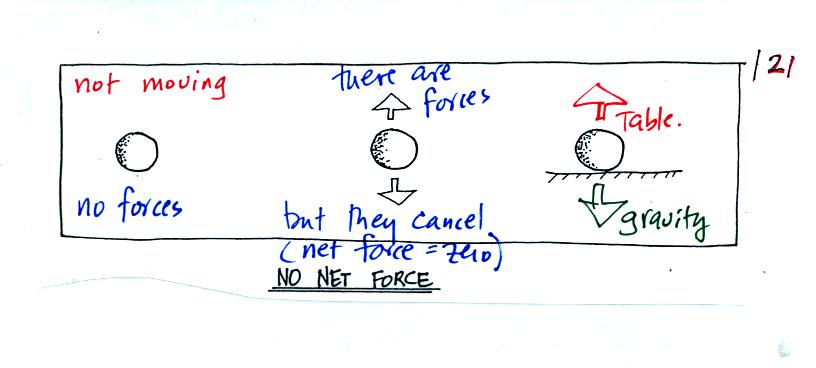
A stationary object is shown in all three figures above (found on p. 121 in the photocopied Class Notes). In the left example there aren't any forces at all being exerted on the object, there is no reason for it to suddenly start to move. In the middle and right examples there are two forces present but they are of equal strength and point in opposite directions. They cancel each other out and the net or total force is zero. Again the stationary object won't suddenly begin to move.

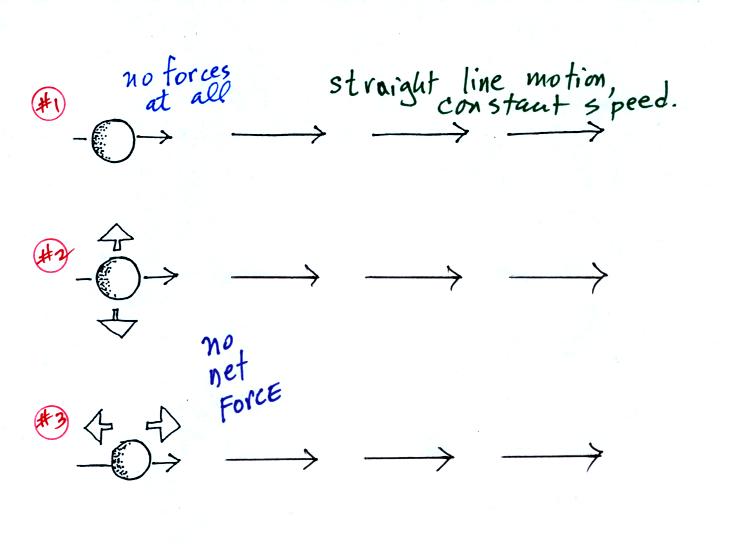
In the first example above there aren't any forces at all. In Examples #2 & #3 and #4 & #5 below (on p. 121 in the photocopied notes) the next force is zero (the two forces present cancel each other out). The object will continue to move in a straight line at constant speed (the thin arrows show the direction of motion, the length of the arrow provides an idea of speed.

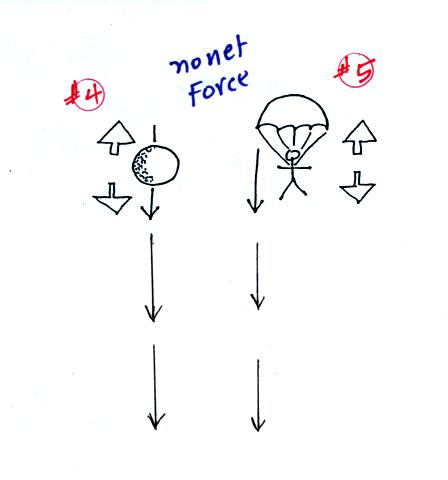
We are used to seeing falling objects pick up speed as they fall. But if an upward drag or friction force becomes strong enough to balance the downward pull of gravity and the net force is zero, the object will fall at constant speed. Parachutists take advantage of this.

Next we will look at the motion that occurs when a net force is present. You should be able to look at the motion and determine whether a net force is needed.

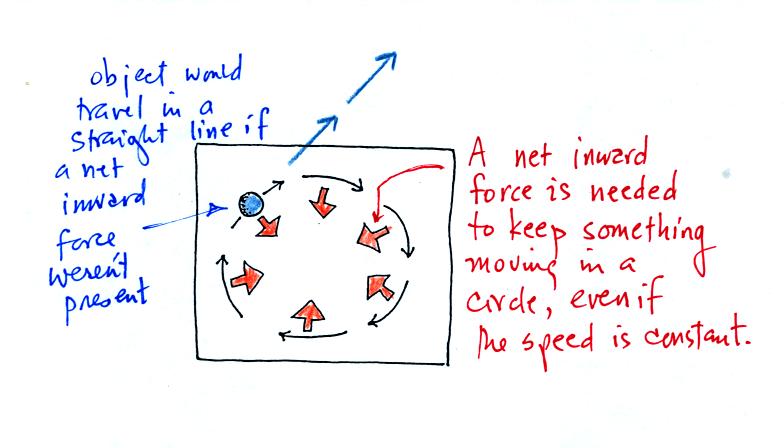
If there were no net force at the point indicated, Newton's 1st law of motion would say the object would travel in a straight line at constant speed (the blue arrows). But the object turns to the right. A force acting perpendiculary and to the right of the object's direction of motion are needed. A net inward force is needed to keep an object moving in a circular path.

An example would be a satellite orbiting the earth

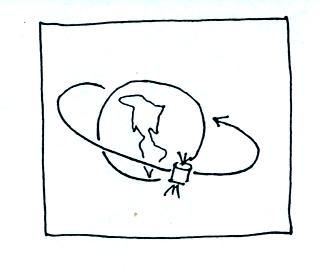
Gravity supplies the net inward force needed to keep the satellite in a circular orbit.

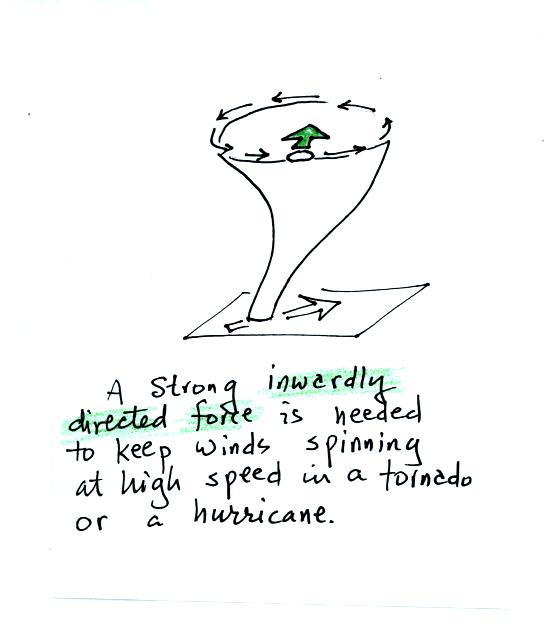
In the case of the rapid winds in a tornado, a very strong inward force is needed (it turns out to be the pressure gradient force (PGF) or pressure difference force).

What we will be most interested in are the upper level winds which, if you remember from earlier in the semester, blow parallel to the contour lines on an upper level chart from west to east.

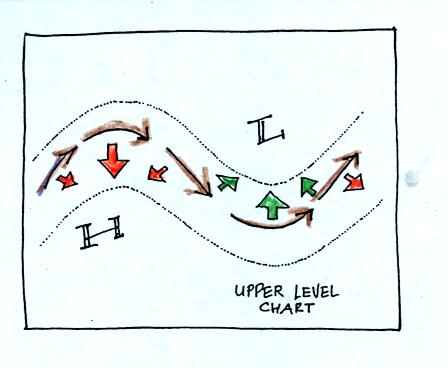
Note that the net force is sometimes to the right of the wind and sometimes to the left of the wind.

The 2nd law of motion really just says that if you exert a net force on an object it will accelerate. Acceleration can mean starting to move, speeding up or slowing down, stopping, or starting moving in a different direction.

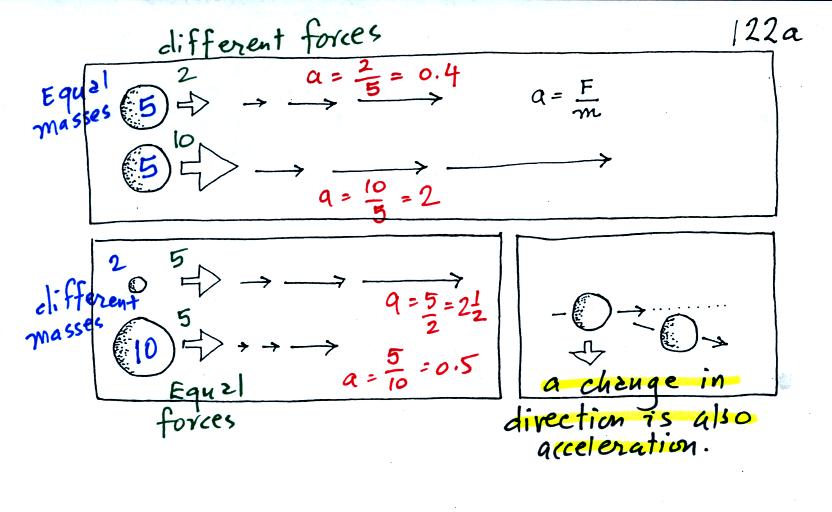
In the first example unequal forces (2 and 10) are applied to equal masses (5 and 5), don't worry about the units. You can calculate the acceleration by dividing force by mass. This gives you the acceleration, the lower object will speed up five times faster than the top object which has a weak force exerted on it.

In the bottom example equal forces (5 and 5) are applied to two different masses (2 and 10). Mass can be thought as being inertia, or resistance to change. An object with a large mass is resistant to a change of direction or speed. A large object is harder to start moving than a small object (imagine pushing a stalled Volkswagen and a stalled Cadillac out of an intersection). The large mass accelerates 5 times more slowly than the smaller mass. Once the large mass gets up to speed however, is is hard to slow it down (a decrease in speed with time is a form of acceleration, we usually call it deceleration)

Note that a change in direction, with or without a change in speed, is also a form of acceleration.

The first two forces above determine upper level winds; we'll study them first. For surface winds you must include the frictional force.

Next we will try to understand what causes these forces. That's pretty easy with the pressure gradient and frictional force, not so easy with the Coriolis force. In each case we will learn rules that determine the direction and the strength of these forces.

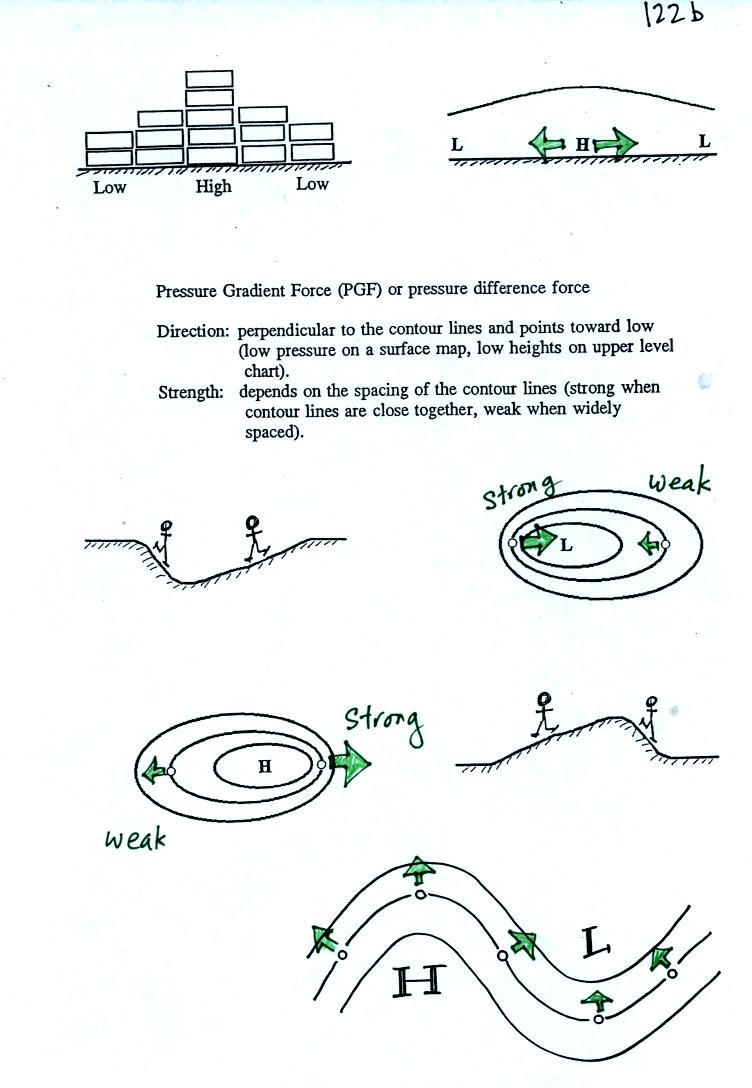
Pressure at any level in the atmosphere is determined by the weight of the air overhead. If you stack up a bunch of bricks as shown at upper left it is easy to understand that the pressure at the bottom center of the picture would be higher than an the edges.

Now imagine carrying a bucket of water to the center of a swimming pool and pouring it out on the water that is already there. You wouldn't be able to pile up water at the center of the pool. As soon as you tried the higher pressure at the bottom of the pool would cause water to flow. The same kind of thing happens with air. The pressure difference force pushes air from high to low pressure.

The rules used to determine the direction and strength of the PGF are given in the center of the picture.

Some examples of PGF force directions and relative strengths are shown at the bottom of the figure. Note the analogy between weather maps and geographical features like hills and valleys.

The pressure gradient force can cause stationary air to begin to blow (there is nothing in the rule that says the strength of the PGF depends on wind speed).

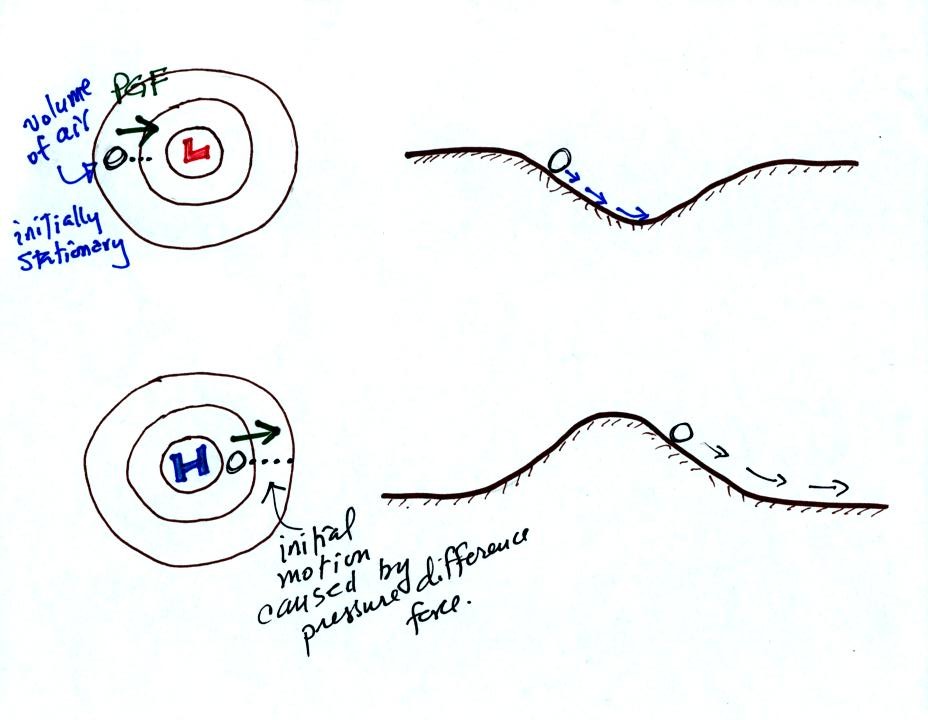
In the top example a stationary volume of air is placed in a center of low pressure. The PGF will cause the air to begin to move toward low pressure in the center of the picture. The dotted line shows the direction of initial motion. This like placing a ball on the side wall of a valley. The ball will roll downhill.

In the second example, a center of high pressure, the PGF causes a stationary volume of air to again begin to move toward low pressure which is outward and away from high pressure. In the analogy a ball placed on the side of a hill will roll downhill and away from the summit.

So given a pressure pattern you should be able to determine the direction of initial motion. The initial motion will always be in the direction of low pressure.

Now on to the Coriolis force.

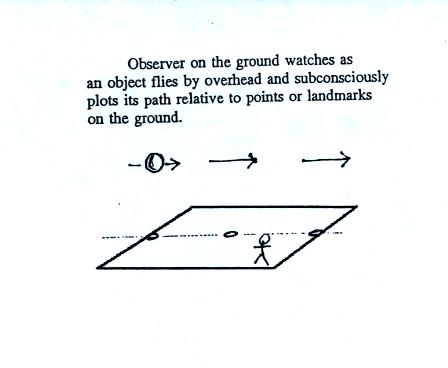
You'll find the figure above on p. 122c in the photocopied Class Notes. Imagine something flies over Tucson. It travels straight from west to east. The next figure shows the path that the saucer followed as it passed over the city.

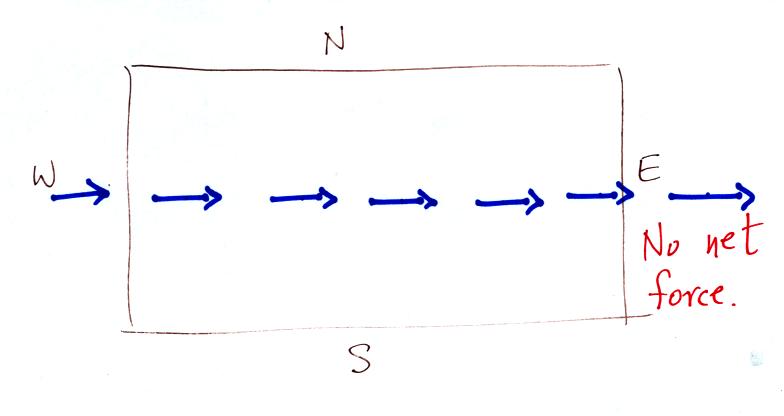
The flying saucer appeared (relative to the ground) to be moving in a straight line at constant speed. You would conclude that there was zero net force acting on the flying saucer.

In this second picture the flying saucer flies by overhead just as it did in the previous picture. In this picture, however, the ground is moving (don't worry about what might be causing the ground to move).

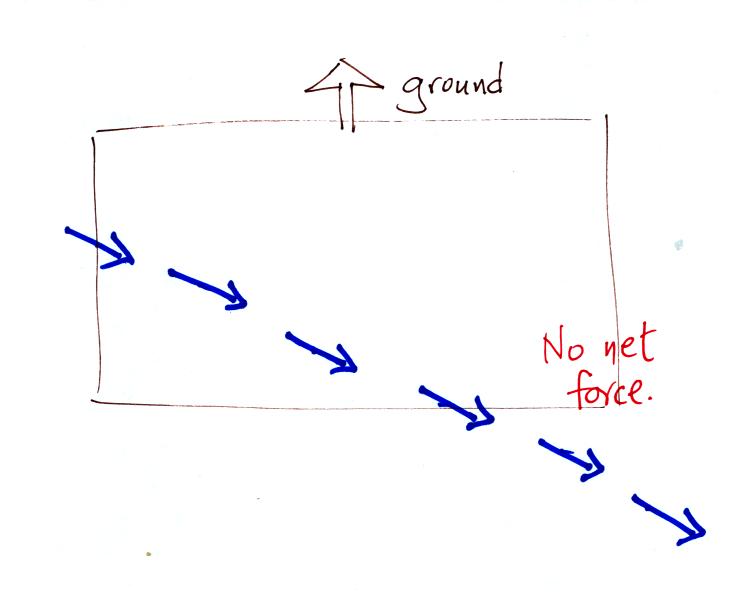
This is the path that you would see relative to the ground in this case. Even though the flying saucer flew from west to east it appears to have been traveling from the NW toward the SE because the ground was moving as the flying saucer passed overhead. Because the motion is still in a straight line at constant speed, you would conclude the net force acting on the flying saucer was zero.

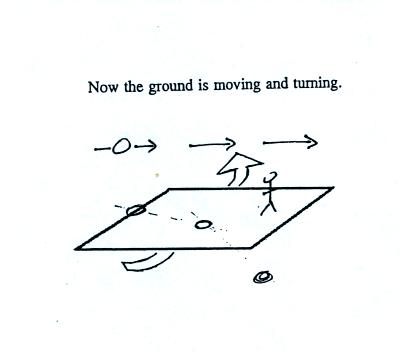
In this last figure the flying saucer flies by again from west to east. In this case however the ground is rotating.

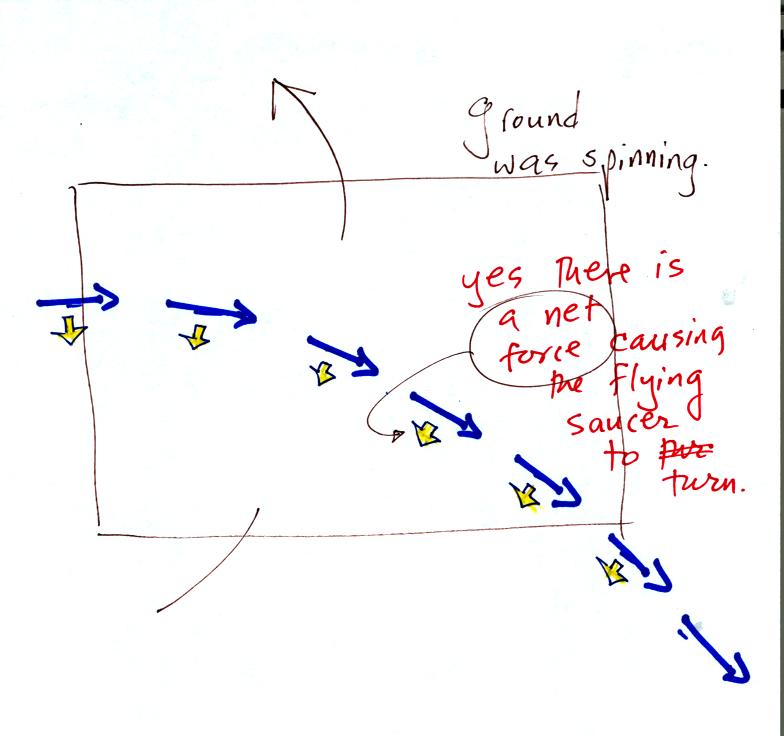
Now the flying saucer appears to have been turning to the right as it passed over Tucson. Because it is no longer traveling in a straight line you would conclude there was a net force acting on the flying saucer. The direction of this net force would be to the right of the motion.

At most locations on the earth the ground is rotating. This is most easily seen at the poles.

Imagine a piece of paper glued to the top of a globe. As the globe spins the piece of paper will rotate. A piece of paper glued to the globe at the equator won't spin, it will flip over. At points in between the paper would spin and flip, the motion gets complicated.

The easiest thing for us to do is to ignore the fact that the ground on which we are standing is rotating. However, if we do that we need to account for the curved paths that moving objects will take when they move relative to the earth's surface. That is what the Coriolis force does.

Here are some rules that you can use to determine the direction and strength of the Coriolis force (whether you understand what causes it or not). It always points in a direction that is perpendicular to the wind, it can't cause the wind to speed up or slow down, it will only change the wind's direction.

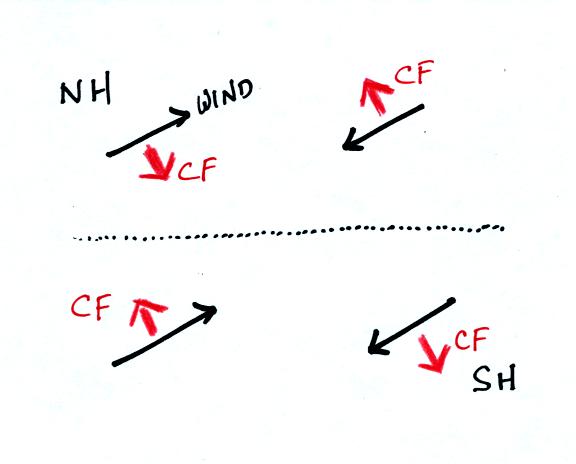
The red arrows show the direction of the CF in the northern and southern hemispheres. The CF is to the right of the wind (you need to look in the direction the wind is blowing, you need to look downstream) in the northern hemisphere and to the left of the wind in the southern hemisphere.