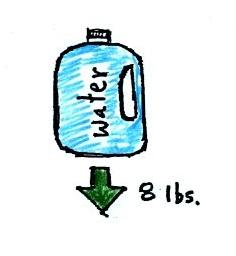The view on the left is
incorrect. The air molecules actually do
not fill the balloon and take up all the available
space.
|
This is the correct
representation. The air molecules are moving
around at 100s of MPH but actually take up little or no
space in the balloon.
|

The air molecules are continually colliding
with the walls of the balloon and pushing outward (this force
divided by area is the pressure). An individual molecule
doesn't exert a very strong force, but there are so many
molecules that the combined effect is significant.

We want to identify the properties or
characteristics of the air inside the balloon that determine
the pressure and then put them together into an equation
called the ideal gas law.
Step #1 - The ideal gas law

In A
the pressure produced by
the air
molecules inside a balloon will
first depend on how many air molecules are there, N. If
there
weren't any air molecules at all there wouldn't be any
pressure.
Here's an example. You're adding air to a tire. As
you add more and more air to something like a
bicycle tire, the
pressure increases. Pressure is directly
proportional to N; an
increase in N causes an increase in P. If N doubles, P
also
doubles (as long as the other variables in the equation don't
change).
In B
air pressure inside a balloon
also
depends on the size of the
balloon. If you try to compress and balloon and
reduce its volume the air pressure increases and
"fights back." A decrease in volume causes an
increase in pressure, that's an inverse
proportionality.
Note
it
is possible to keep pressure constant by changing N
and V
together in just the right kind of way. This is
what happens in
Experiment #1 that some students are working on.
Here's a little
more detailed look at that experiment.
|

|
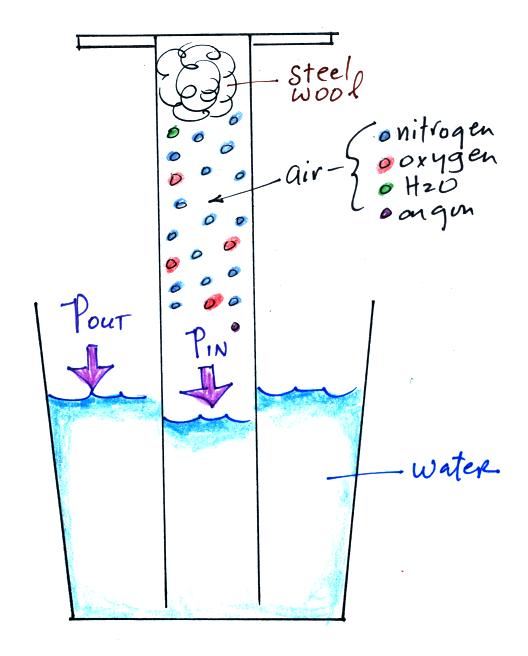
An
air sample is trapped together with some steel wool
inside a
graduated cylinder. The cylinder is turned
upside down and the
open end is stuck into a glass of water sealing off
the air sample from
the rest of the atmosphere. This is shown at
left
above. The pressure of air outside the cylinder
tries to push water into the cylinder, the pressure of
the air inside keeps the water out.
Oxygen in the cylinder reacts with steel wool to form
rust.
Oxygen is
removed from the air sample which causes N (the total
number of air
molecules) to decrease. Removal of oxygen would
ordinarily cause
a drop in Pin
and
upsets the balance between Pin
and Pout
. But,
as
oxygen
is
removed,
water
rises
up
into
the
cylinder
decreasing
the
air
sample
volume.
The decrease in V causes Pin
to increase. What actually happens is that N and
V both decrease together in the same relative amounts
and
the air sample pressure remains constant.
If you were to remove 20% of the air molecules, V would
decrease
to 20% of its original value and pressure would stay
constant. It
is the change in V that you can measure and use to determine
the oxygen
percentage concentration in air.
Part
C: Increasing
the temperature of the gas in a balloon will cause the
gas molecules to
move more quickly (kind of like "Mexican
jumping
beans"). They'll collide with the walls of
the
balloon
more frequently and rebound with greater force.
Both will
increase the pressure.

You shouldn't throw
a can of spray paint
into a fire because the temperature will cause the
pressure inside the
can to increase and the can could explode.
Surprisingly, as explained in Part
D,
the pressure
does
not depend on the mass of the
molecules. Pressure doesn't depend on the composition of
the
gas. Gas molecules with a lot of mass will move slowly,
the less
massive molecules will move more quickly. They both will
collide
with the walls of the container with the same force.
The figure below (which replaces the bottom of p. 51 in the
photocopied
ClassNotes) shows two forms of the ideal gas law. The
top
equation is the one we just "derived" and the bottom is a
second
slightly
different version. You can
ignore the
constants k and R if you are just trying to understand how a
change in
one of the variables would affect the pressure. You only
need the
constants when you are doing a calculation involving numbers
and units (which we
won't be doing).
The ratio N/V is similar to density
(mass/volume). That's
where
the ρ (density) term in the second equation
comes from.
Step #2 Charles' Law
In Charles Law we assume
that the
pressure of a parcel of air will remain constant (parcel
is just
another word for volume). Changing the temperature
of a volume of
air will cause a change in density and volume and pressure
will stay
constant. This is an important situation because
this is how
volumes of air in the atmosphere behave.
This is probably the most difficult part of today's class
and is worked out in lots of detail.
We start with a balloon of air. The air inside
and outside
the balloon (or parcel) are exactly the same.
Note the pressure pushing inward is balanced by the
pressure of the air
inside the balloon that is pushing outward. If we
change
something inside the balloon that upsets this pressure
balance, the
balloon would expand or shrink until the pressures were
again in
balance.
Volumes of air in the atmosphere will always try to
keep the
pressure of the air inside the parcel constant (P
inside is always trying to stay equal to P outside).
That's why
we say air in the atmosphere obeys Charles' Law.
First let's imagine warming the air inside a
balloon. We'll won't
change the temperature of the air outside the balloon.
Increasing the temperature will momentarily increase
the
pressure. This creates an imbalance. Now that
P inside is
greater than P outside the
balloon will expand.
Increasing the volume causes the pressure to start to
decrease.
The balloon will keep expanding until P inside is back in
balance
with P outside.
We're left with a balloon that is larger, warmer, and
filled with lower
density air than it was originally.
The pressures inside and outside are again the same.
The pressure
inside is back to what it was before we warmed the air in
the
balloon. You can increase the temperature and volume
of a parcel together in a way that keeps pressure constant
(which is
what Charles' law requires). Or you can increase the
temperature
and decrease the density together and keep the pressure
constant.
In nature the change in temperature and volume occur
simultaneously. It's like jumping from the first to
the last step above.
Warming some air in a balloon will cause volume to
increase & density to decrease in order to keep
pressure constant. Pressure stays constant, a change
in temperature causes a change in volume and density.l
We can go through the same kind of reasoning and see what
happens
if we cool the air in a parcel. I've included all
the steps
below; that wasn't done in
class.
We'll start with a parcel of air that has the same
temperature and
density as the air around it.
We'll cool the air inside the parcel. The air
outside stays
the same.
Reducing the air temperature causes the pressure of the
air inside
the balloon to decrease. Because the outside air
pressure is
greater than the pressure inside the balloon the parcel is
compressed.
The balloon will get smaller and
smaller (and the pressure inside will get bigger and
bigger) until the
pressures inside and outside the balloon are again
equal. The
pressure inside is back to the value it had before you
cooled the air
in the parcel.
The first and last steps, without all the intermediate
and momentary details, are shown below.
Cooling some air will cause volume to decrease and
density to increase while pressure stays constant.
If you want to skip all the details and just remember
one thing,
here's what I'd recommend
Charles
Law can be demonstrated by dipping a balloon in
liquid
nitrogen. You'll find an explanation on the top of
p. 54 in the
photocopied ClassNotes.
The balloon shrinks down to practically nothing when
dunked in the
liquid nitrogen. It is filled with very cold, very
high density
air. When the balloon is pulled from the liquid
nitrogen and
starts to warm up it expands. Density in the balloon
decreases. The volume and temperature keep changing
in a way that kept pressure constant (pressure inside the
balloon is
staying equal to the air pressure outside the
balloon).
Eventually the balloon ends
up back at room temperature (unless it pops while warming
up).
Step #3 Vertical forces acting on
parcels of air
And finally the last step toward understanding why warm air
rises
and cold air sinks. We'll have a look at the forces that
act on
parcels of air in the atmosphere. This is
something we have already covered. The information below
is
found on p. 53
in the photocopied
ClassNotes.
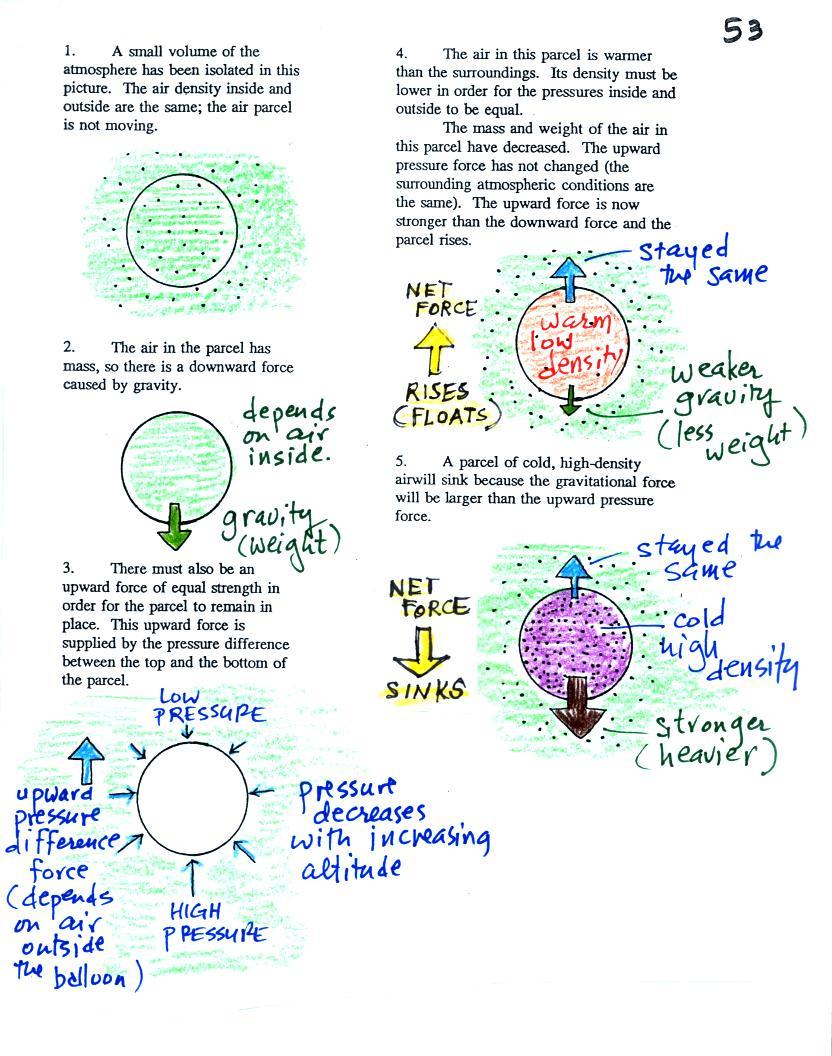
Basically it comes down to this - there are two forces
acting on a parcel of
air in
the atmosphere. They are shown on the left
hand side
of the figure above.
The first force is gravity, it pulls downward. The
strength of the gravity
force
(the weight of the air in the parcel) depends
on the mass of the air inside
the parcel.
Second there is an upward pointing pressure difference
force.
This
force is
caused by the air outside
(surrounding) the parcel. Pressure decreases with
increasing
altitude. The pressure of the air at the bottom of a
parcel
pushing upward is slightly stronger than the pressure of the
air at the
top of the balloon that is pushing downward. The overall
effect
is an upward pointing force.
When the air inside a parcel is exactly the same as the air
outside,
the two forces are equal in strength and cancel out. The
parcel
is
neutrally buoyant and it wouldn't rise or sink, it would just
sit in
place.
Now have a look at the right hand side of the figure.
If you replace the air inside the balloon with warm low
density
air, it
won't weigh as much. The gravity force is weaker.
The
upward
pressure difference force doesn't change (because it is
determined by
the air outside the balloon which hasn't changed) and ends up
stronger
than the
gravity force. The balloon will rise.
Conversely if the air inside is cold high density air, it
weighs
more. Gravity is stronger than the upward pressure
difference
force and the balloon sinks.
It all comes down to how the density of the in parcel
compares to
the density of the air surrounding the parcel. If the
parcel is
filled with low density air it will rise. A parcel full
of high
density air will sink.
We did a short demonstration to show how
density can
determine
whether an object or a parcel of air will rise or sink.
We used
balloons filled with helium (see bottom of p. 54 in
the photocopied Class
Notes). Helium is less dense than air even when it has
the same
temperature as the surrounding air. A
helium-filled balloon doesn't need to warmed up in order to
rise.

We dunked the helium-filled balloon
in some liquid nitrogen to cool
it
and to cause the density of the helium to increase. When
removed
from the liquid nitrogen the balloon didn't rise, the gas
inside was
denser than the surrounding air (the purple and blue balloons
in the
figure above). As the balloon warms and expands
its density decreases. The balloon at some point has the
same
density as the air around it (green above) and is neutrally
bouyant (it's still cooler than the surrounding air).
Eventually
the balloon becomes less dense that the
surrounding air (yellow) and floats up to the ceiling (which
in ILC 150
is about 30 feet high)
Something like this happens in the
atmosphere. I didn't show the
following picture in class.
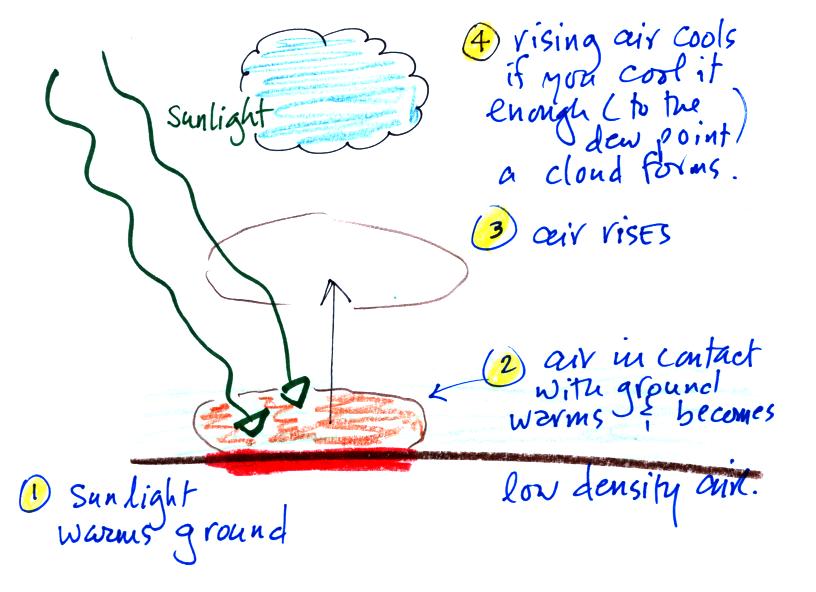
Sunlight shines through the
atmosphere. Once it reaches the
ground at (1) it is absorbed and warms the
ground. This in turns warms air in contact with the
ground
(2) As this air warms, its density starts to
decrease. When
the density of the warm air is low enough,
small "blobs" of air separate from the air layer at the ground
and
begin
to rise, these are called "thermals." (3) Rising air
expands and
cools (we've haven't covered
this yet and it might sound a little contradictory). If
it cools
enough (to the dew point) a cloud will
become visible as shown at Point 4. This whole process
is called convection; many of our summer
thunderstorms start this way.
Here's another way of trying to
understand why warm air rises and cold air sinks - Archimedes
Law or Principle. It's a perhaps simpler way
of understanding the
topics. A bottle of water can help you to visualize the
law.
A gallon of
water weighs about 8 pounds (lbs). I wouldn't want to
carry that much water on a hike unless I really thought I
would need it.
If you submerge the gallon jug of water in a swimming pool,
the
jug
becomes, for all intents and purposes, weightless. That
seems
kind of amazing. Archimedes'
Law (see figure below, from p. 53a in the photocopied
ClassNotes)
explains why this is true.
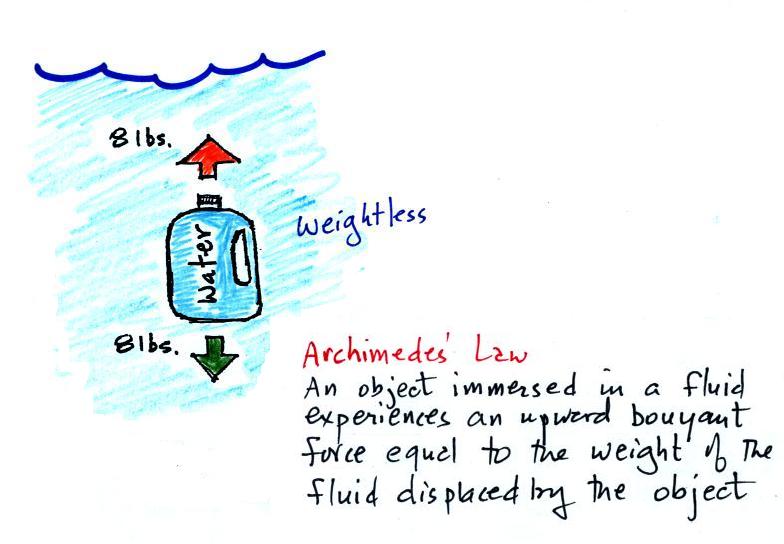
Archimedes first of all tells you
that the surrounding fluid will exert an upward pointing
buoyant force
on the submerged water bottle. That's why the submerged
jug can
become weightless.
Archimedes law also tells you how to figure
out how strong the buoyant force will be. In
this
case the 1 gallon bottle will displace 1 gallon of
pool water. One
gallon of pool
water weighs 8 pounds. The upward buoyant force will be
8 pounds,
the same as the downward force. The two
forces are equal and opposite.
What Archimedes law doesn't really tell you is what causes
the
upward
buoyant
force. You should know what the force is - it's the
upward pressure difference force.
Now we imagine pouring out all the water and filling the 1
gallon
jug
with air. Air is about 1000 times less dense than water;
compared
to water, the jug
will weigh practically nothing.
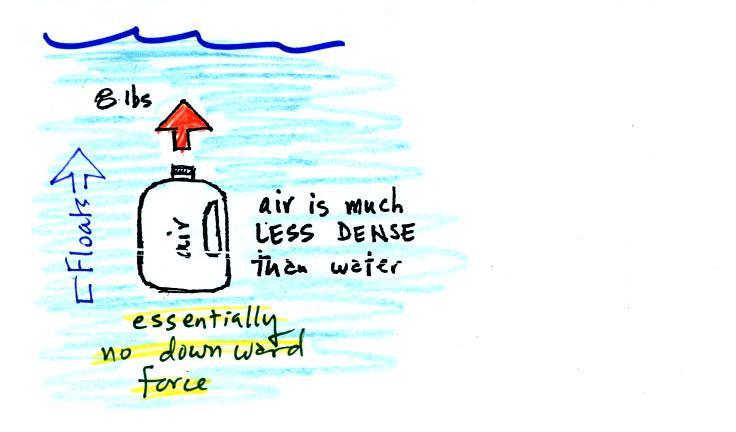
If you
submerge the jug of air in a
pool
it will displace 1 gallon of
water
and experience an 8 pound upward buoyant force again.
Since there
is no downward force the jug will float.
One gallon of sand (which is about 1.5 times denser than
water)
jug weighs 12 pounds.
The jug of sand will sink because the
downward force is greater than the upward force.
You can sum all of this up by saying
anything that is less dense than water will float in water,
anything that is more dense than water will sink in water.
Most types of wood will float (ebony and
ironwood will sink). Most rocks sink (pumice is an
exception).
The same reasoning applies to air in the atmosphere
though it's harder to appreciate because air is invisible.

Air that is less dense
(warmer)
than the air around it will
rise.
Air that is more dense (colder) than the air around it will
sink.
Here's a little more
information
about
Archimedes that I didn't mention in
class.
There's a colorful demonstration that shows how small
differences
in density
can determine whether an object floats or sinks.
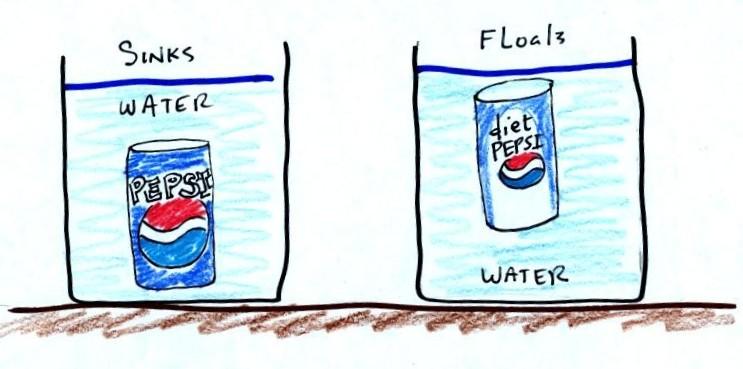
A can of regular Pepsi was
placed in a beaker of water.
The
can
sank. A can of Diet Pepsi on the other hand floated.
Both cans are made of aluminum which has a density almost
three
times
higher than water; aluminum by itself would sink. The
drink
itself is largely water. The
regular soda also has a lot of high-fructose
corn
syrup, the diet soda
doesn't. The mixture of water and corn syrup has a
density
greater than plain
water. There is also a little air (or perhaps carbon
dioxide gas)
in each can (the diet soda probably wouldn't float if it
weren't for the gas in the can.
The average density of the can of regular soda (water
& corn
syrup
+
aluminum + air) ends up being slightly greater than the
density of
water. The average density of the can of diet soda
(water +
aluminum + air) is slightly less than the density of water.
In some respects people in swimming pools are like cans
of regular
and
diet soda. Some people float (they're a little less
dense than
water), other people sink (slightly more dense than
water).