Storm systems in the tropics
(0 to 30 degrees latitude) generally move from east to west in
both hemispheres. At middle latitudes (30 to 60
degrees), storms move in the other direction, from west to
east. To understand why this is true we need to learn
something about the earth's global scale pressure and wind
patterns. There's a good chance that we won't cover this
in class. Rather it will be the subject of a future
optional assignment.
What about these three examples. Is there
a net inward or outward force in each case. You should
now know that there is a net inward force in the 1st
example. What about the next two. The 3rd
example usually causes people the most trouble. You'll
find the answer to this question at the very end of today's
notes.
Now we'll start to look at the forces
that cause the wind to blow.
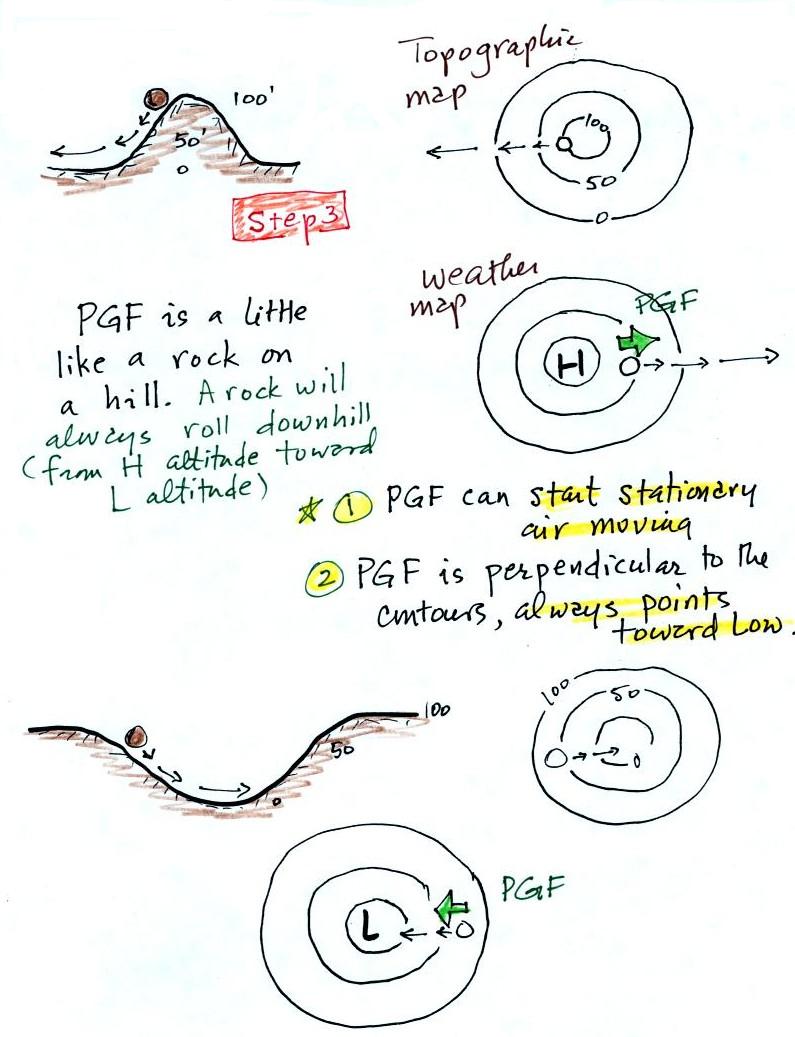
Pressure Gradient Force (PGF)
Air moving inward toward low pressure or outward away
from high pressure is similar to a rock rolling down and away
from the summit of a hill or inward toward the bottom of a
depression. The pressure gradient force always points
perpendicular to the contour lines on a map and toward low
pressure. The PGF will cause stationary air to begin to
move (it will always move toward low pressure).
Use the following figure to test yourself. With an
arrow draw the direction of the PGF at each of the points in the
figure. You'll find the answers at the end of today's
notes.
Coriolis
Force
The Coriolis force is caused
by the rotation of the earth. We'll learn more about the
Coriolis force on Thursday. The CF points perpendicular
to the wind and is to the right or left depending on
hemisphere. Be sure you are looking in the direction the
wind is blowing, looking downstream when determining the
direction of the CF.
The CF can only change the wind's direction. It can't
cause the wind to speed up or slow down.
There isn't any Coriolis force when the wind is calm.
Coriolis force is zero at the equation because that's where
the CF changes direction. Hurricanes don't form at the
equator because there is no Coriolis force there.
Time now to begin applying what we've learned.
We start with some stationary air at Point 1. Because
the air is stationary, there is no Coriolis force. There
is a PGF force, however. The PGF at Point 1 starts
stationary air moving toward the center of low pressure (just
like a rock would start to roll downhill).
Once the air starts to move, the CF causes it to turn to the
right (because this is a northern hemisphere chart).
This is happening at Point 2 (the dots show the initial motion
of the air). As the wind speeds up the CF
strengthens. The wind eventually ends up at Point 3
blowing parallel to the contour lines and spinning in a
counterclockwise direction. Note that the inward PGF is
stronger than the outward CF. This results in a net
inward force, something that is needed anytime wind blows in a
circular path.
See if you can figure
out what would happen with low pressure in the Southern
Hemisphere.
We start again with some
stationary air at Point 1 in this figure. You'll find
the details at the end of today's notes.
Next we'll look at what happens around
upper level high pressure
Here initially stationary
air at Point 1 begins to move outward in response to an
outward pointing pressure gradient force (PGF). Once
the air starts to move, the Coriolis force (CF) will cause
the wind to turn to the right. The wind ends up
blowing in a clockwise direction around the high. The
inward pointing CF is a little stronger than the PGF so
there is a net inward force here just as there was with the
two previous examples involving low pressure. An
inward force is needed to keep anything moving in a circular
path.
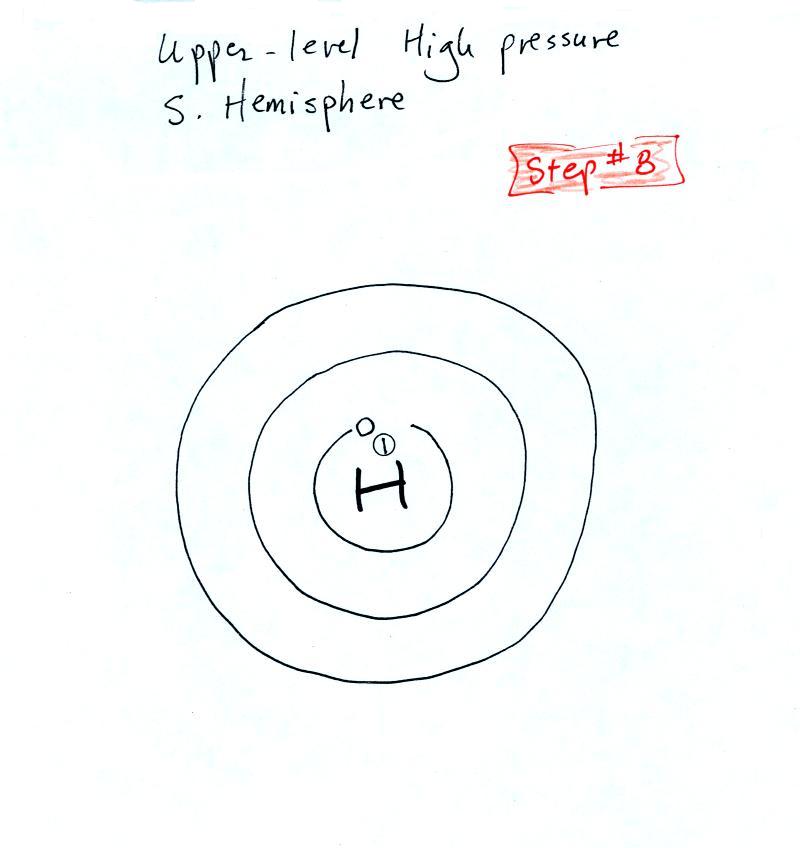
This is a southern hemisphere upper level center of high
pressure. You should be able to figure out how the
winds will blow in this case. You'll find
the answer at the end of today's notes.
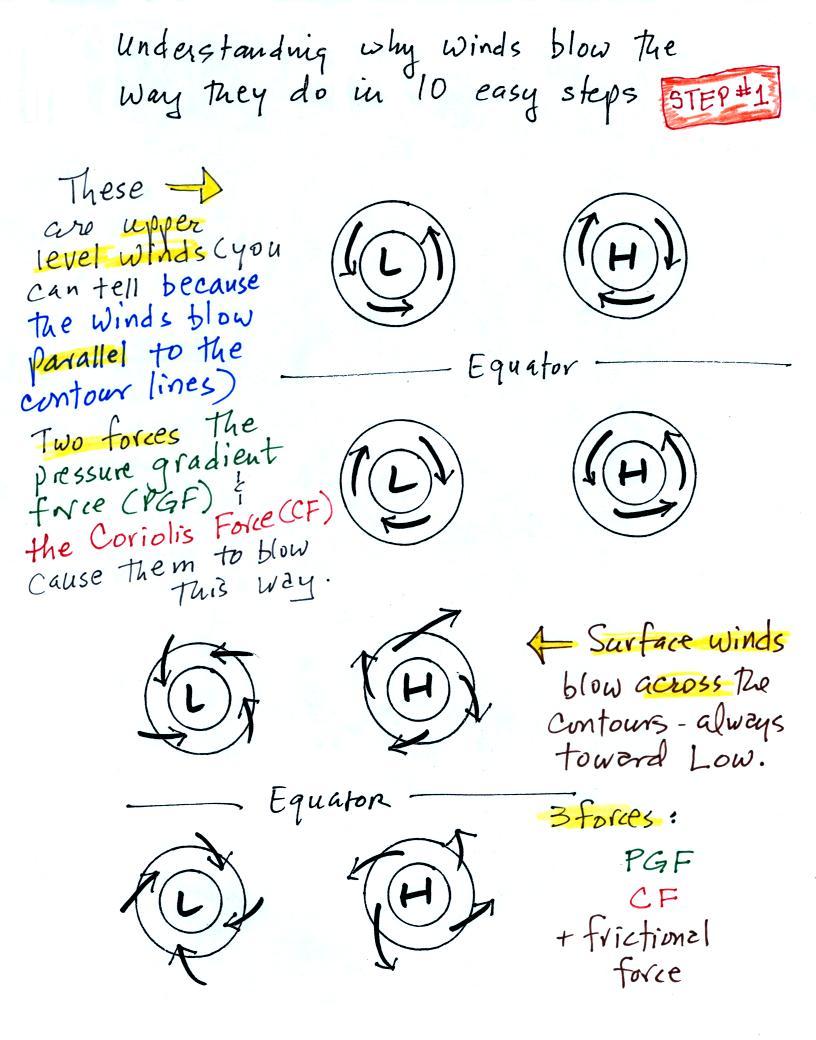
Upper level winds blow parallel to the contour
lines. Now we'll try to understand why friction causes
surface winds to blow across the contour lines (always
toward low pressure).

We add friction in the second picture. It points in a
direction opposite the wind and can only slow the wind
down. The strength of the frictional force depends on
wind speed (no frictional force if the wind is calm) and the
type of surface the wind is blowing over (less friction when
wind blows over a smoother surface like the ocean,
more frictional force when the wind is blowing over a
rougher surface like land).
Slowing the wind weakens the CF and it can no longer balance
the PGF (3rd figure). The stronger PGF causes the wind
to turn and start to blow across the contours toward
Low. This is shown in the 4th figure. Eventually
the CF and Frictional force, working together, can balance
out the PGF. The net force would again
equal zero and the wind would blow in a straight line at
constant speed across the contours toward low pressure.
This is where we finished in class. But I've added
Step #10 and a little information about the Coriolis Force
below.
What we've learned from the straight contour
example, namely that the winds will blow across the contours
toward low pressure can be applied to a curved contour
pattern. This figure wasn't
shown in class.
If you take a small little
piece of a curved pattern and magnify it, it will look
straight. We can mostly apply what we
learned about straight contours to curved contours.
Now our last step, surface winds blowing around H and
L in the NH and SH.

It is easy to figure out which of the figures are
centers of low pressure (the wind blows inward toward the
center of the picture) The winds are spiraling inward
in the top and bottom examples (1 and 3). These must
be surface centers of low pressure. The winds are
spiraling outward from the centers of high pressure (2 and
4).
Now you probably don't want to figure out which of these are
northern and which are southern hemisphere pictures.
It is probably best to remember one of the pictures.
Remember in 1, for example, that surface winds spin
counterclockwise and spiral inward around centers of low
pressure in the northern hemisphere (something we
learned early in the semester). Then remember that
winds spin in the other direction and blow outward around
high pressure in the northern hemisphere (2). The
spinning directions of the winds reverse when you move from
the northern to the southern hemisphere. Thus you find
clockwise spinning winds and inward motion around low
pressure (3) and counterclockwise and outward spiraling
winds around high pressure in the southern hemisphere.
Converging winds cause air to rise. Rising air expands
and cools and can cause clouds to form. Clouds and
stormy weather are associated with surface low pressure in
both hemispheres. Diverging winds created sinking wind
motions and result in clear skies.
Somethings change when you move form the northern to the
southern hemisphere (direction of the spinning winds).
Sometimes stay the same (winds spiral inward around centers
of low pressure in both hemispheres, rising air motions are
found with centers of low pressure in both hemispheres).
Here's something else not yet covered in class, an explanation
of the cause of the Coriolis force. You'll
probably find this a little confusing. The pictures that
follow aren't in the ClassNotes.
Imagine
something flies over Tucson. It travels straight
from west to east at constant speed. You
would,
more
or
less
subconsciously,
plot
its path relative to the ground.
The
next
figure
shows
the
path
that the object would appear to follow as it passed over
the city.
Here's the path the moving
object would appear to follow relative to the
ground. Based on this straight line, constant speed
trajectory you'd conclude there was no net force acting on
the object (and again no net force doesn't mean there
aren't any forces, just that they all cancel each other
out so the total force is zero).
In this second picture the
object flies by overhead just as it did in the previous
picture. In this picture, however, the ground is moving
(don't worry about what might be causing the ground to
move).
It's kind of like walking across the moving sidewalk at an
airport with wet paint on your feet. What sort of track
would you leave behind?
Even though you moved perpendicularly to the sidewalk, the
foot prints would appear at an angle.
In the case of the object flying by overhead
The path, relative to the ground, would look something like
this. It would no longer appear to be moving
from W to E but rather from the NW toward the SE. It's
still straight line motion at constant speed, though,
so you conclude there was no net force acting on the object.
Now the ground is moving and
also spinning. The object's
motion hasn't changed.
The path of the object plotted on the
ground appears to be curved. But remember that's
relative to the ground and the ground is spinning. We
could take the ground's motion into account or just ignore
it. In the latter case you'd conclude that there was a
net force perpendicular and to the right of the moving
object. This net force would be needed to explain the
curved path that the object appears to be following.
And that's what the Coriolis forcedoes.
At most locations on the earth the
ground IS
rotating (and this is what Foucault's Pendulum
demonstrates). This is most easily seen at the poles.

Here finally are answers to the four questions embedded in
today's notes

A net inward force is needed in all three
cases. It's just the strength of the force required.