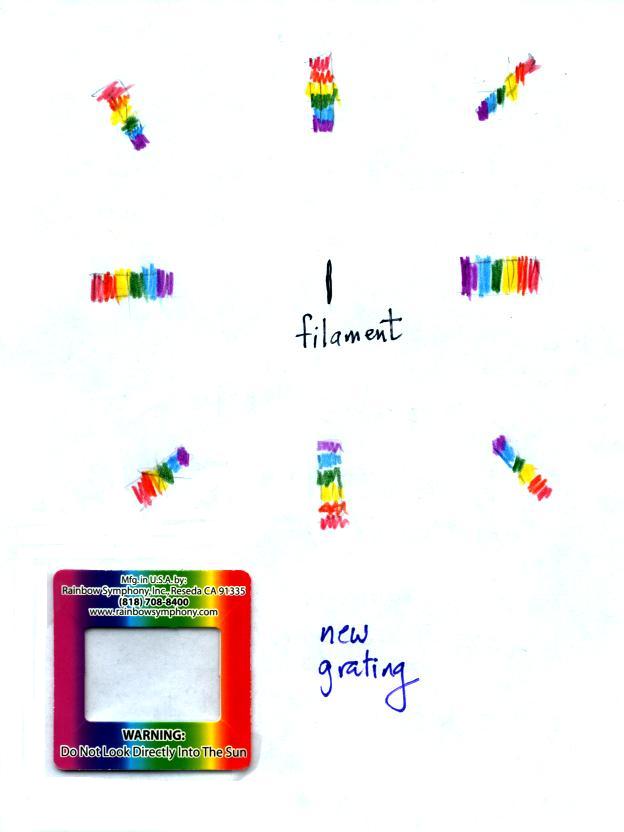Tuesday Oct. 14, 2014
I heard a couple of Willie Nelson songs at happy hour last
Friday and it reminded me that I really needed to feature some of
his music before class. We had time for "Breathe",
"All of Me",
"My Window
Faces the South", "Home in San
Antone" (4:08), and "On the Road
Again" (3:06) though not necessarily in that order.
The Experiment #2 reports, the Upper Level Charts Optional
Assignment and the Surface Weather Map Analysis were all collected
today. You should expect to get all of them back, graded,
next week sometime.
The 1S1P reports on Scattering of Sunlight have been graded and
were returned today. There a good chance that some new
topics will become available by Thursday this week so that I can
make an announcement before the quiz.
The Experiment #3 materials should be available for checkout
before the quiz on Thursday. I'll also have some Expt. #2
materials for students that were able to check them out during the
first round. Students will then be able to perform the
experiment and write their report on the Expt. #3 schedule.
I.e. reports from both experiments will be due Tue., Nov. 4.
Quiz #2 is Thursday this week. See the Quiz #2 Study Guide for more details
including the times and locations of the Tuesday and Wednesday
afternoon reviews.
At last, It's time to tackle
electromagnetic (EM) radiation, the 4th and most important of the
energy transport processes.
Many textbooks depict EM radiation with a wavy line like shown
above. They don't usually explain what the wavy line
represents.
The wavy line just connects the tips of a bunch of "electric
field arrows". But what exactly are electric field arrows (you
might have heard the term electric field vectors in a physics
course).

To understand electric
fields we need to first review a couple of rules
concerning static electricity.
Static electricity is something you're most
likely already familiar with. Believe it or not there
is even a National Static Electricity Day (Jan. 9)
Here are some pictures I found online.

|

|

|
This girl became charged with static
electricity while jumping on a trampoline and
illustrates the repulsive force of like charges (her
hair and body are all charged up with charge of the same
polarity).
The charge on her hair is trying to get as far away
from charge on her body. People's hair will
sometimes stand on end under a thunderstorm. In
that case it represents a very situation to be in.
This photo was a National Geographic Magazine 2013
Photo Contest winner (source)
|
A cat covered in styrofoam "peanuts".
Here the cat and the "peanuts" have opposite charges
and are attracted to each other. Being
a cat owner I would worry about the cat swallowing one
of the peanuts and possibly choking. (source)
|
I'm not entirely sure what
this is. Is it a dog, is it
alive? It is so clean it must never
go outdoors. I'm not sure it is charged
up. It's hair might be like this all the
time. (source)
|
The static electricity
rules are found at the top of p. 59 in the photocopied
ClassNotes
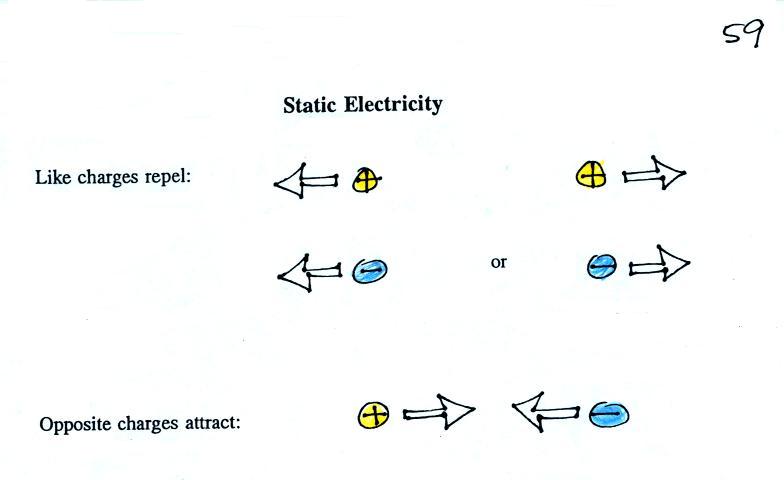
Two electrical charges with the same polarity (two positive
charges or two negative charges) push each other apart.
Opposite charges are attracted to each other.
In this figure a positive charge has
been placed at 3 locations around a center charge.
The 3 charges will all be repelled by the center charge,
the outward force exerted on each is shown in
blue. The forces range from weak to strong
depending on the distance between the two
charges.
Now instead of drawing in the center
charge we have the pattern of electric field arrows that
it would produce.
An electric
field arrow
shows the direction and
gives an idea of the strength
of the electrical force
that would be exerted on a positive
charge
The E field arrows
show you what would happen to a + charge
at three different locations within the pattern.
You can also use the pattern of electric field arrows to
determine what will happen to a -
charge also. I didn't
mention this in class.
For a negative charge the force will point in a direction
opposite the E field arrow.
Here are a couple of questions to test your
understanding. These weren't
shown in class.

First what polarity of charge must be on ground to cause the
charges in the figure below to move as they are doing.
Then what direction does the electric field arrow point at a
location just above the ground where the two charges are found.
Here's a second somewhat harder question (it's also on the Quiz #2 Study Guide).
What is the direction of the electric field arrow at Point X halfway between a +
and a - charge.
You'll find answers to both questions at the end of today's notes.
Now we'll use what we know about electric
fields to start to understand electromagnetic radiation.
You'll find most of the following on p. 60 in the photocopied
ClassNotes.
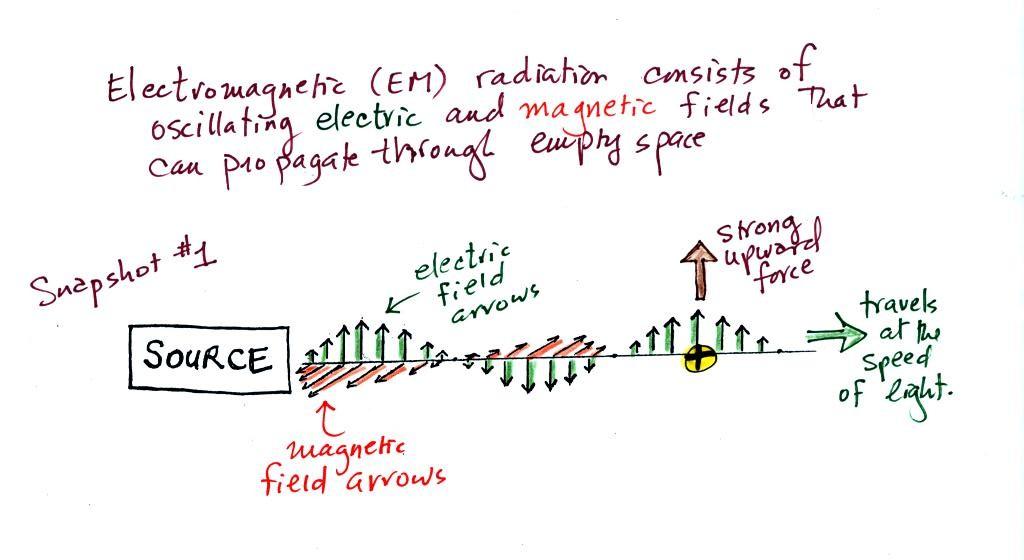
We imagine turning on a source of EM radiation and then a very
short time later we take a snapshot. In that time the EM
radiation has traveled to the right (at the speed of
light). The EM radiation is a wavy pattern of electric and
magnetic field arrows. We'll ignore the
magnetic field lines. The E field lines sometimes point
up, sometimes down. The pattern of electric field arrows
repeats itself.
Note the + charge near
the right side of the picture. At the time this picture was
taken the EM radiation exerts a fairly strong upward force
on the + charge (we use the
E field arrow at the location of the + charge to determine the direction and strength of
the force exerted on the +
charge).
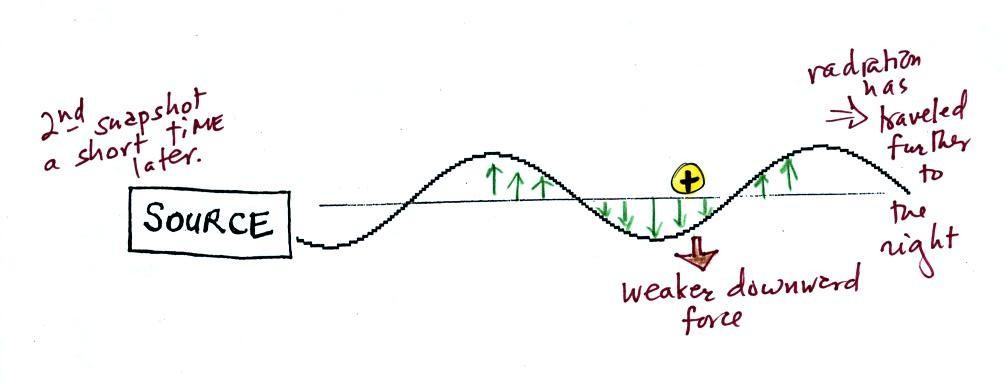
Th picture above was taken a
short time after the first snapshot after the radiation had
traveled a little further to the right. The EM radiation
now exerts a somewhat weaker downward force on the + charge.
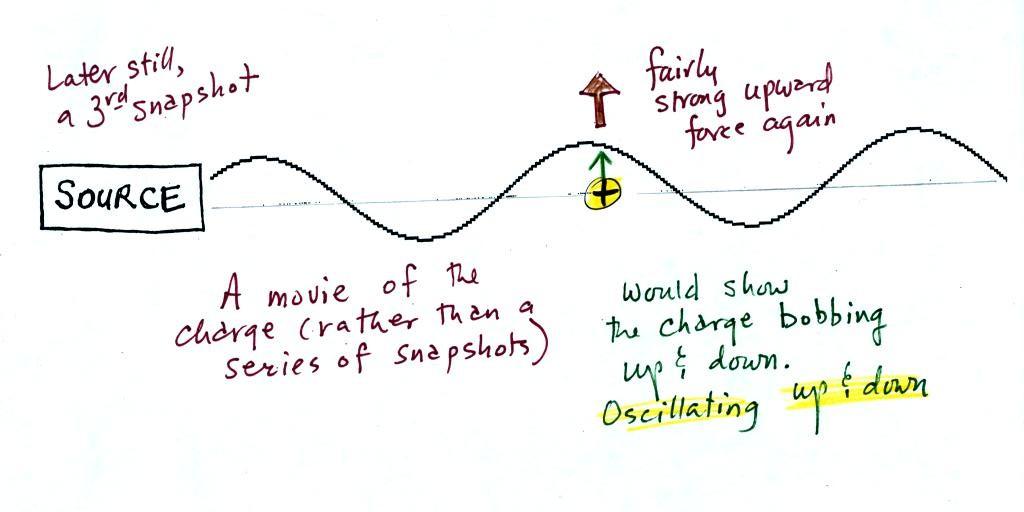
A 3rd snapshot taken a short
time later. The +
charge is now being pushed upward again.
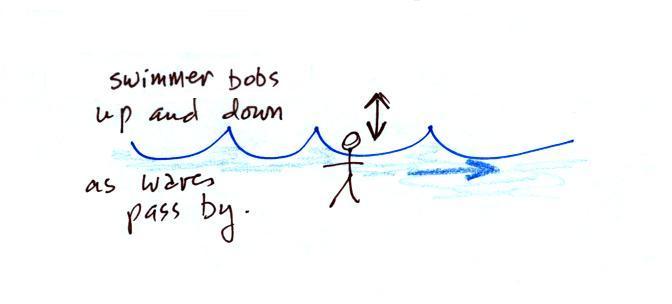
A movie of the + charge,
rather than just a series of snapshots, would show the charge
bobbing up and down much like a swimmer in the ocean would do as
waves passed by.
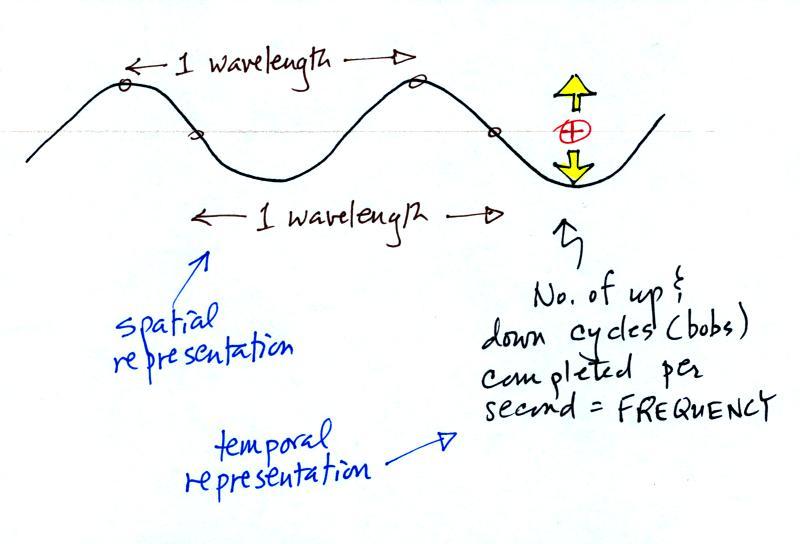
The wavy pattern used to depict
EM radiation can be described spatially (what you would see in a
snapshot) in terms of its wavelength, the distance between
identical points on the pattern.
Or you can describe the radiation temporally using the
frequency of oscillation (number of up and down cycles completed
by an oscillating charge per second). By temporally we mean
you look at one particular fixed point and look at how things
change with time.
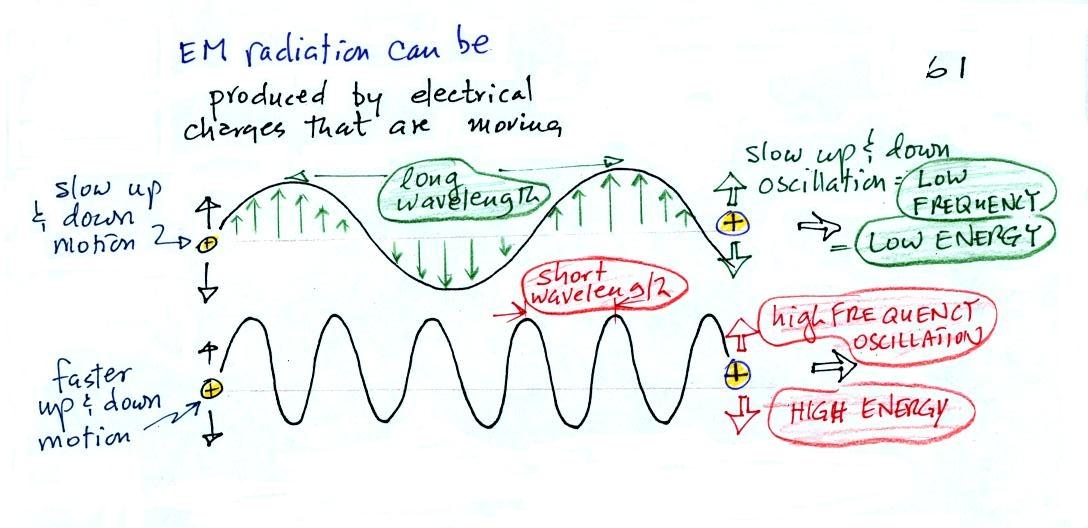
EM radiation can be created when
you cause a charge to move up and down. If you move
a charge up and down slowly (upper left in the figure above) you
would produce long wavelength radiation that would propagate out
to the right at the speed of light. If you move the charge
up and down more rapidly you produce short wavelength radiation
that propagates at the same speed.
Once the EM radiation encounters the charges at the right
side of the figure above the EM radiation causes those charges
to oscillate up and down. In the case of the long
wavelength radiation the charge at right oscillates
slowly. This is low frequency and low energy motion.
The short wavelength causes the charge at right to oscillate
more rapidly - high frequency and high energy.
These three characteristics: long
wavelength / low frequency / low energy go
together. So do short wavelength /
high frequency / high energy. Note that the
two different types of radiation both propagate at the same
speed.
The
following figure illustrates how energy can be transported
from one place to another (even through empty space) in the
form of electromagnetic (EM) radiation.

You add energy when you cause an
electrical charge to move up and down and create the EM
radiation (top left).
In the middle figure, the EM
radiation that is produced then travels out to the right (it
could be through empty space or through something like the
atmosphere).
Once the EM radiation encounters an electrical charge at
another location (bottom right), the energy reappears as the
radiation causes the charge to move. Energy has been
transported from left to right.
This is really just a partial list of some of the different
types of EM radiation. In the top list, shortwave
length/high energy forms of EM radiation are on the left (gamma
rays and X-rays for example). Microwaves and radiowaves are
longer wavelength/lower energy forms of EM radiation.
We will mostly be concerned with just ultraviolet light (UV),
visible light (VIS), and infrared light (IR). These are
shown on an expanded scale below. Note the micrometer
(millionths of a meter) units used for wavelength for these kinds
of light. The
visible portion of the spectrum falls between 0.4 and 0.7
micrometers. UV and IR light are both
invisible. All of the vivid colors shown above are just EM
radiation with slightly different wavelengths. When you see
all of these colors mixed together, you see white light.
I've tried to demonstrate this using laser pointers.
It is too hard to get them adjusted so that the small spots of
colored light all fall on top of each other on the screen at the
front of the room. And even if you do the small spot of
light is so small that it's hard to see clearly in a large
classroom (you need to do the experiment on a piece of paper a few
feet away).
Here's the basic idea, you mix red green and blue light
together. You see white light were the three colors overlap
and mix in the center of the picture above.
We spent most of the rest of the
class learning about some rules governing the emission of
electromagnetic radiation. Here they are:
1.
Everything
warmer than 0 K will emit EM radiation. Everything in the
classroom: the people, the furniture, the walls and the floor,
even the air, are emitting EM radiation. Often
this radiation will be invisible so that we can't see it and
weak enough that we can't feel it (or perhaps because it is
always there we've grown accustomed to it and ignore it).
Both the amount and kind (wavelength) of the emitted radiation
depend on the object's temperature. In the classroom most
everything has a temperature of around 300 K and we will see
that means everything is emitting infrared (IR) radiation with a
wavelength of about 10µm.
2.
The second
rule allows you to determine the amount of EM radiation (radiant
energy) an object will emit. Don't worry about the units
(though they're given in the figure below), you can think of
this as amount, or rate, or intensity. Don't worry about σ (the Greek character rho) either, it is just
a constant. The amount depends on
temperature to the fourth power. If the temperature of an
object doubles the amount of energy emitted will increase by a
factor of 2 to the 4th power (that's 2 x 2 x 2 x 2 = 16).
A hot object just doesn't emit a little more energy than a cold
object it emits a lot more energy than a cold object. This
is illustrated in the following figure:
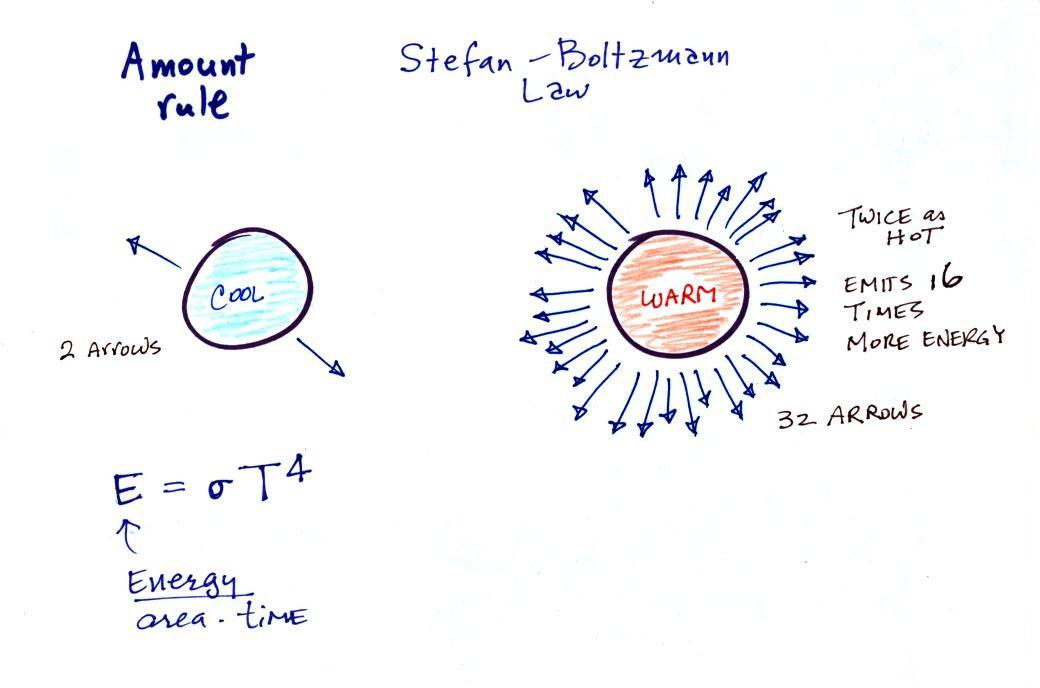
The cool object is emitting 2
arrows worth of energy. This could be the earth at 300
K. The warmer object is 2 times warmer, the earth heated
to 600 K. The earth then would emit 32 arrows (16 times
more energy).
The earth has a temperature of 300 K. The sun is 20
times hotter (6000 K). Every square foot of the sun's
surface will emit 204 (160,000)
times more energy per second than a square foot of the
earth's surface.
3.
The third
rule tells you something about the kind of radiation emitted by
an object. We will see that objects usually emit radiation
at many different wavelengths but not in equal amounts.
Objects emit more of one particular wavelength than any of the
others. This is called λmax
("lambda max", lambda is the Greek character used to represent
wavelength) and is the wavelength of maximum emission. The
third rule allows you to calculate λmax.
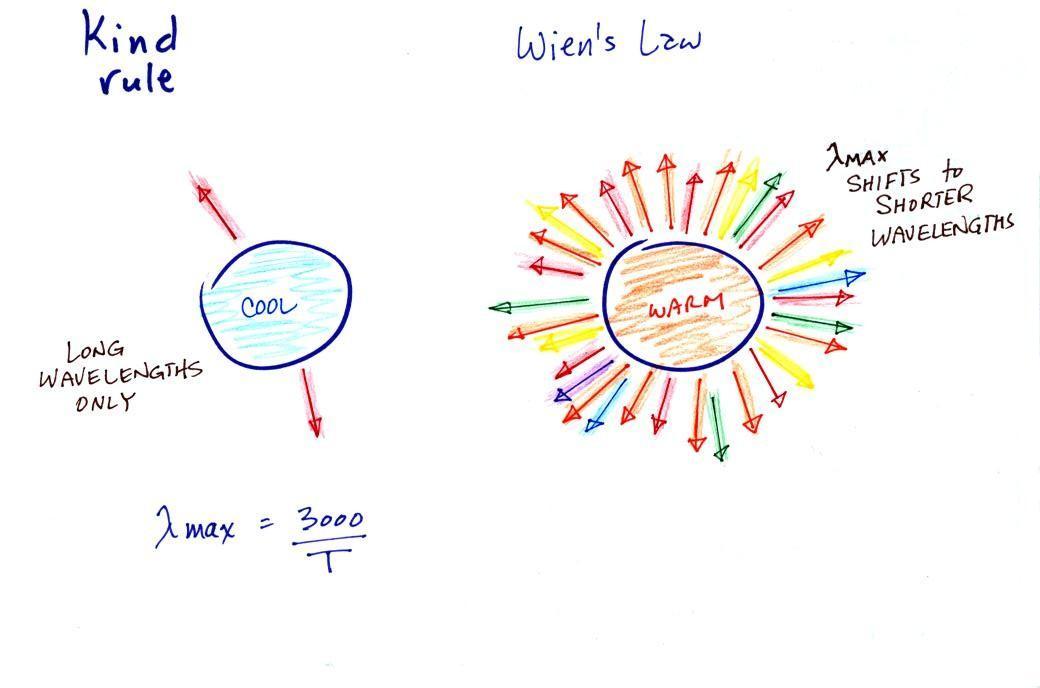
The tendency for warm objects to emit radiation at shorter
wavelengths is shown below.
The cool object is probably emitting infrared light (that
would be the case for the earth at 300 K) so the 2 arrows of
energy are colored red. The warmer object will also emit IR
light but also shorter wavelengths such as yellow, green, blue,
and violet (maybe even some UV if it's hot enough). Remember
though when you start mixing different colors of visible light
you get something that starts to look white. The cool
object might glow red, a hotter object would appear white.
Here's another way of trying to understand what Wien's Law and the
Stefan-Boltzmann law mean (the graph below is on the bottom of p.
65 in the ClassNotes).
1.
Notice first
that both and warm and the cold objects emit radiation over a
range of wavelengths (the curves above are like quiz scores, not
everyone gets the same score, there is a distribution of
grades). The warm object emits all the wavelengths the
cooler object does plus lots of additional shorter wavelengths.
2.
The peak of
each curve is λmax the
wavelength of peak emission (the object emits more of that
particular wavelength than any other wavelength). Note
that λmax has
shifted toward shorter wavelengths for the warmer object.
This is Wien's law in action. The warmer object is
emitting lots of types of short wavelength radiation that the
colder object doesn't emit.
3.
The area
under the warm object curve is much bigger than the area under
the cold object curve. The area under the curve is the
total radiant energy emitted by the object. This
illustrates the fact that the warmer object emits a lot more
radiant energy than the colder object.
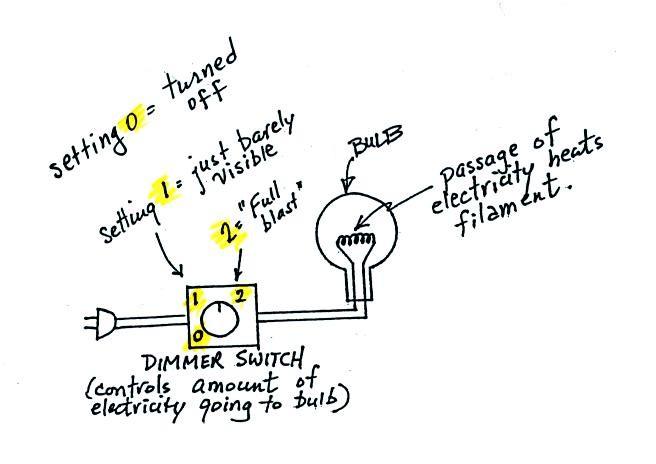
It is relatively easy to see Stefan-Boltzmann's law and Wien's
Law in action. The class demonstration consisted of an
ordinary 200 W tungsten bulb is connected to a dimmer switch (see
p. 66 in the photocopied ClassNotes). We'll be looking at
the EM radiation emitted by the bulb filament.
The graph at the bottom of p. 66 has been split up into 3
parts and redrawn for improved clarity.

We start with the bulb turned off (Setting 0). The
filament will be at room temperature which we will assume is
around 300 K (remember that is a reasonable and easy to remember
value for the average temperature of the earth's surface).
The bulb will be emitting radiation, it's shown on the top graph
above. The radiation is very weak so we can't feel
it. The wavelength of peak emission is 10
micrometers which is long wavelength, far IR radiation so we can't
see it.
Next we use the dimmer switch to just barely turn the bulb on
(the temperature of the filament is now about 900 K). The
bulb wasn't very bright at all and had an orange color.
This is curve 1, the middle figure. Note the far left end
of the emission curve has moved left of the 0.7 micrometer mark
- into the visible portion of the spectrum. That is what
you were able to see, just the small fraction of the radiation
emitted by the bulb that is visible light (but just long
wavelength red and orange light). Most of the radiation
emitted by the bulb is to the right of the 0.7 micrometer mark
and is invisible IR radiation (it is strong enough now that you
could feel it if you put your hand next to the bulb).
Finally we turn on the bulb completely (it is a 200 Watt bulb
so it got pretty bright). The filament temperature is now
about 3000K. The bulb is emitting a lot more visible
light, all the colors, though not all in equal amounts.
The mixture of the colors produces a "warm white" light.
It is warm because it is a mixture that contains a lot more red,
orange, and yellow than blue, green, and violet light. It
is interesting that most of the radiation emitted by the bulb is
still in the IR portion of the spectrum (lambda max is 1
micrometer). This is invisible light. A tungsten
bulb like this is not especially efficient, at least not as a
source of visible light.
You were able to use one of the diffraction gratings handed
out in class to separate the white light produced by the bulb
into its separate colors.
When you looked at the bright white bulb filament through one
of the diffraction gratings the colors were smeared out to the
right and left as shown at left below.
Some of the gratings handed out in class behaved a little
differently and spread out the colors horizontally, vertically,
and diagonally (right sketch above)
Ordinary tungsten bulbs (incandescent
bulbs) produce a lot of wasted energy. This is because
they emit a lot of invisible infrared light that doesn't light
up a room (it will warm up a room but there are better ways of
doing that). The light that they do produce is a warm
white color (tungsten bulbs emit lots of orange, red, and
yellow light and not much blue, green or violet).
Energy efficient compact fluorescent lamps (CFLs) are being
touted as an ecological alternative to tungsten bulbs because
they use substantially less electricity, don't emit a
lot of wasted infrared light, and also last longer. CFLs
come with different color temperature ratings.
The bulb with the hottest temperature rating (5500 K ) in the
figure above is meant to mimic or simulate sunlight
(daylight). The temperature of the sun is 6000 K and lambda
max is 0.5 micrometers. The spectrum of the 5500 K bulb is
similar.
The tungsten bulb (3000 K) and the CFLs with temperature
ratings of 3500 K and 2700 K produce a warmer white.
Three CFLs with the temperature ratings above were set up in
class so that you could see the difference between warm and cool
white light. Personally I find the 2700 K bulb "too warm,"
it makes a room seem gloomy and depressing (a student in class
once said the light resembles Tucson at night). The 5500 K
bulb is "too cool" and creates a stark sterile atmosphere like you
might see in a hospital corridor. I prefer the 3500 K bulb
in the middle.
The figure below is from an
article on compact fluorescent lamps in Wikipedia for those
of you that weren't in class and didn't see the bulb
display. You can see a clear difference between
the cool white bulb on the left in the figure below and the warm
white light produced by a tungsten bulb (2nd from the left) and 2
CFCs with low temperature ratings (the 2 bulbs at right).
There is one downside to these energy efficient CFLs. The
bulbs shouldn't just be discarded in your ordinary household trash
because they contain mercury. They should be disposed of
properly (at a hazardous materials collection site or perhaps at
the store where they were purchased).
It probably won't be long before LED bulbs begin
to replace tungsten and CFL bulbs. The price has dropped
significantly in just the last 6 months or so.
LED stands for light emitting diode. We won't be looking
at them in detail except to say that a single LED can produce only
a single color, it can't produce white light. What is done
instead is to put three small LEDS producing red green and blue
light in close proximity. When they are illuminated the
three colors mix together to produce white light.
The basic idea is shown below (the photo is from
Wikipedia)
When red green and blue all mix together you see white
light.
Here's something we didn't have time for
in class, but I'll stick it in anyway - the light
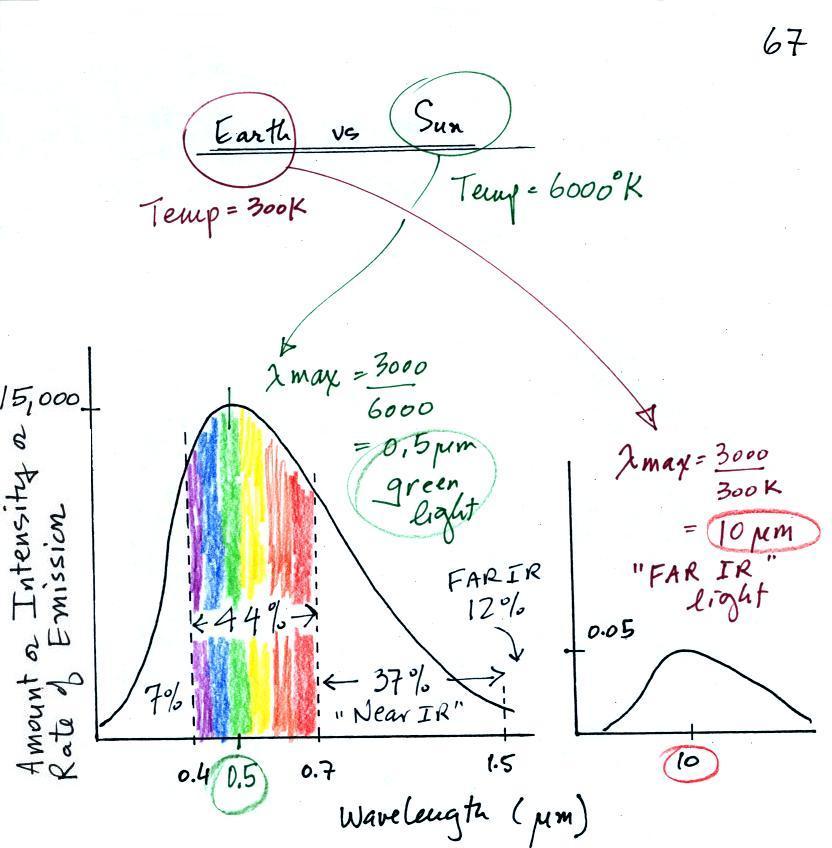
emitted by the sun and the earth.
The curve on the left is for the sun. The surface of the
sun has a temperature of 6000 K so we can use Wien's law to
calculate λmax
. It turns out to be 0.5 micrometers. This is green
light; the sun emits more green light
than any other kind of light. The sun doesn't appear green
because it is also emitting lesser amounts of violet, blue,
yellow, orange, and red - together this mix of colors appears
white (it's a cooler white than emitted by a tungsten
bulb). 44% of the radiation emitted by the sun is visible
light, Very nearly half of sunlight (49%) is IR light (37%
near IR + 12% far IR). 7% of sunlight is ultraviolet
light. More than half of the light emitted by the sun (the
IR and UV light) is invisible.
100% of the light emitted by the earth (temperature = 300 K) is
invisible far IR light. The wavelength of peak emission for
the earth is 10 micrometers.
Because the sun (surface of the sun) is 20 times hotter
than the earth the sun's surface emits energy at a much higher
rate than the earth (160,000 times higher). Note
the vertical scale on the earth curve is different than on the sun
graph. If both the earth and sun were plotted with the same
vertical scale, the earth curve would be much too small to be
seen.
Here are the answers to the two electric field questions
embedded earlier in the notes.
#1. The ground can be either negatively or positively
charged. If the ground were negatively charged the positive
charge would be attracted to the ground and the
negative charge repelled and pushed upward. That's not
what is happening. So the ground must be positively charged.
The positive charge is creating the force that causes the
positive charge to move upward. So that too must be
direction that the electric field arrow is pointing.
#2. To answer the first question we
imagine placing a + charge at Point X.
The center charge will be repelled by the charge on the left
and attracted to the charge on the right. The center charge
would move toward the right.
The electric field arrow shows the direction of the force on
the center charge. The electric field arrow should point
toward the right.