Tuesday Jan. 27, 2009
In class today a mixture of theoretical type stuff and some examples of
instruments that could be used to measure lightning and thunderstorm
electric fields (that make use of some of these concepts).
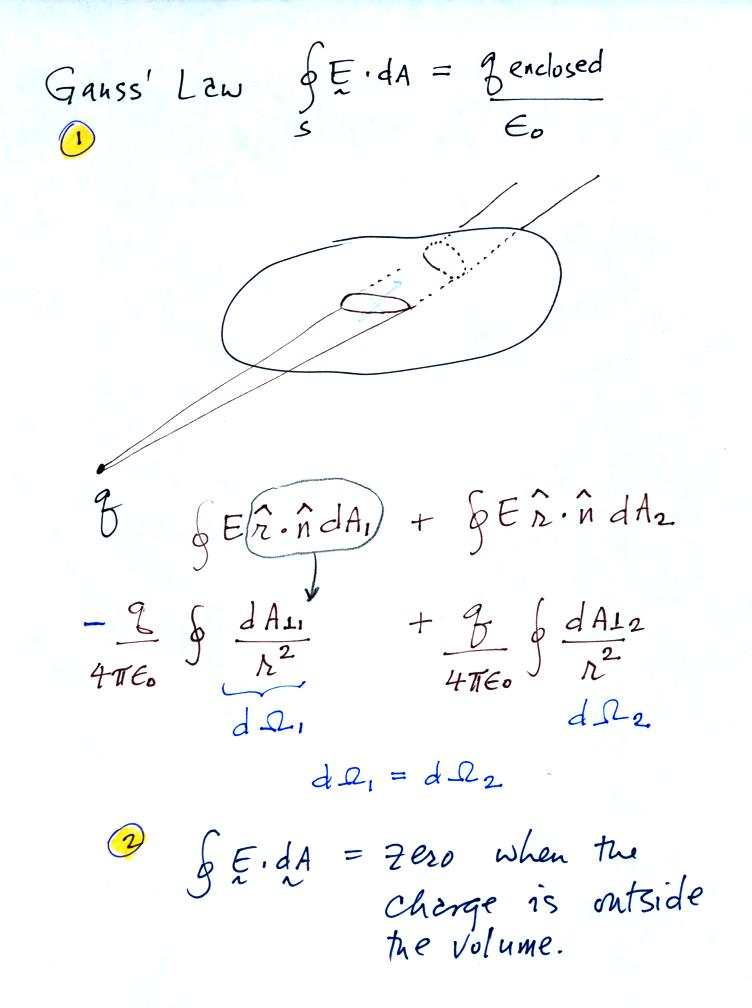
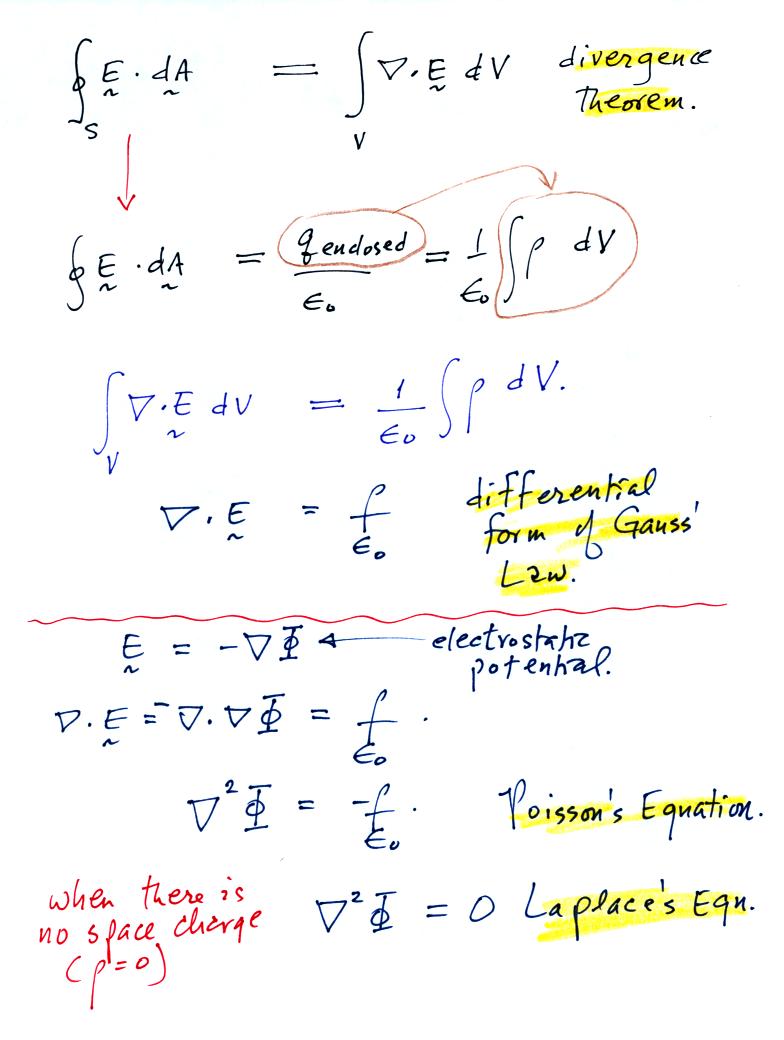
Point 1 is the integral form of Gauss' Law that was derived in
class last Thursday. It is a relatively simple thing to show that
if the charge q is located outside the volume V then the surface
integral of E is zero.
Homework #1 pt. 1 was handed out at this
point. I would suggest using the differential form of Gauss' Law
to answer the first question. Here
also is a handout with the various operators (gradient, divergence,
etc) in cartesian, cylindrical, and spherical polar coordinates.
If you write the electric field as the gradient of the electrostatic
potential and then substitute that into Gauss' Law you can obtain
Poisson's Equation. Laplace's equation applies in situtations
where the volume space charge density is zero.
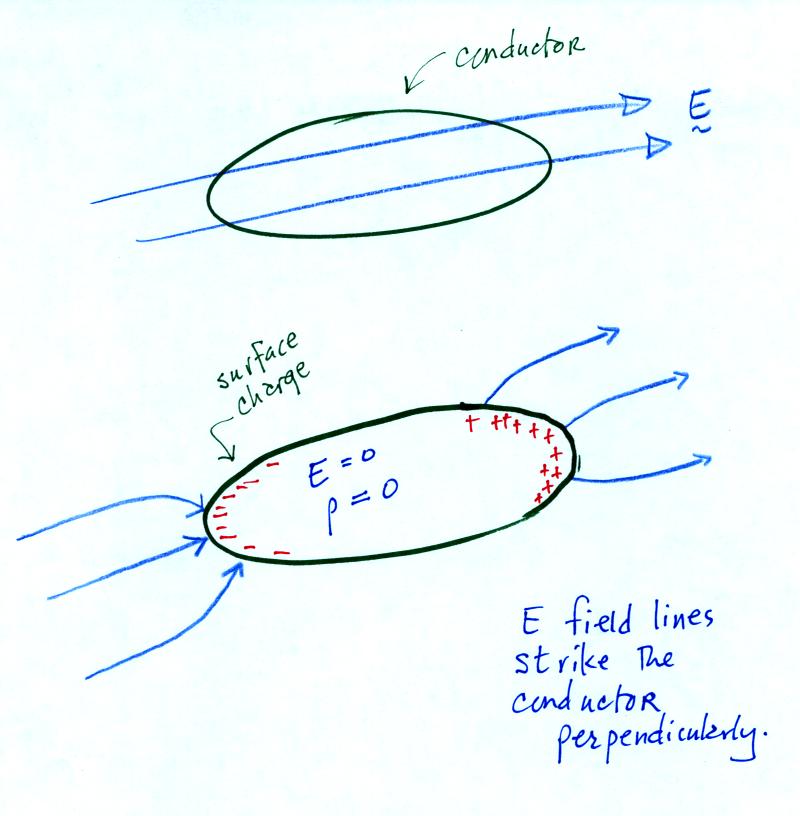
Next we
imagine placing a conductor in an electric field
Free electrons inside the conductor will quickly move around and
redistribute themselves in such a way that they will cancel out the
field in the conductor (as the electrons move they leave behind
positively charged atoms). Very quickly the field inside the
conductor will be zero. There is also no space charge inside the
conductor, all the charge is distributed along the surface on the
conductor. The electric field lines in the vicinity of the
conductor will be distorted and will strike the surface of the
conductor perpendicular (if there were any tangential component,
charges would move and cancel it out).
Next we'll use Gauss' Law to determine a relationship between the
surface charge density and the electric field strength at the surface
of a conductor.
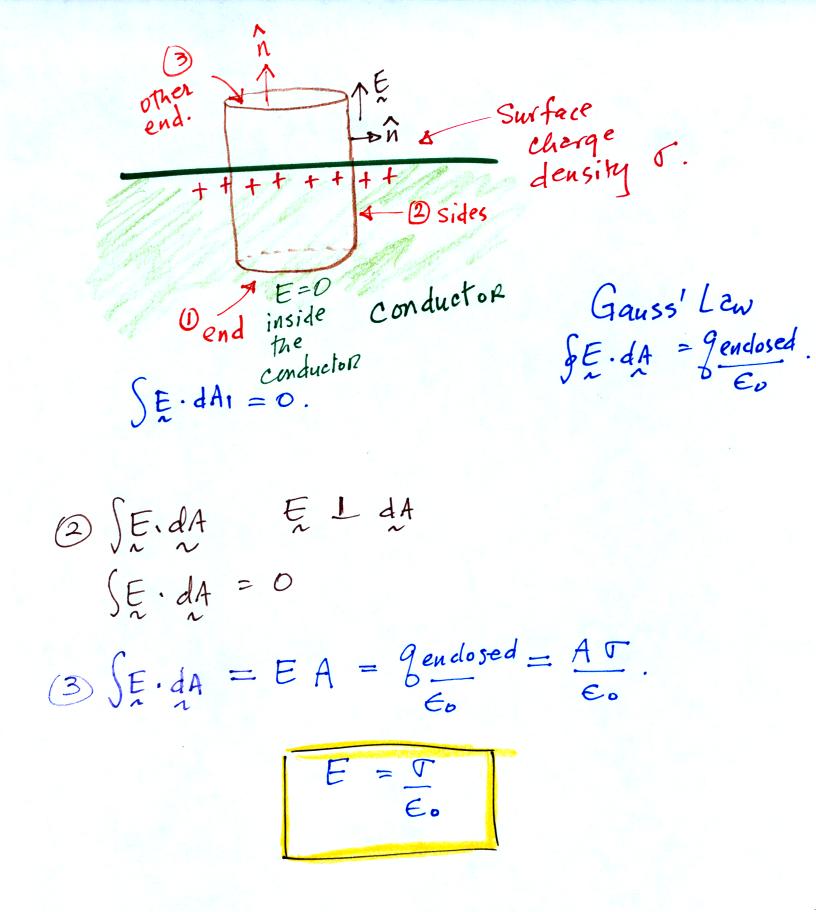
1. The E field is zero inside the conductor. So you get no
contribution to the surface integral from the bottom end of the
cylinder.
2. Along the sides of the cylinder, E is perpendicular to
the vector normal to the surface. So there is no contribution to
the surface integral from the sides of the cylinder.
3. The only contribution comes from the top end of the
cylinder. E and the normal vector are parallel. So the
contribution from the top end is just E A, where A is the area of the
top end of the cylinder. The charge enclosed is just A σ, where σ is
the surface charge density. The electric field
at the surface of the conductor is perpendicular to
the conductor and has the value highlighted in yellow.
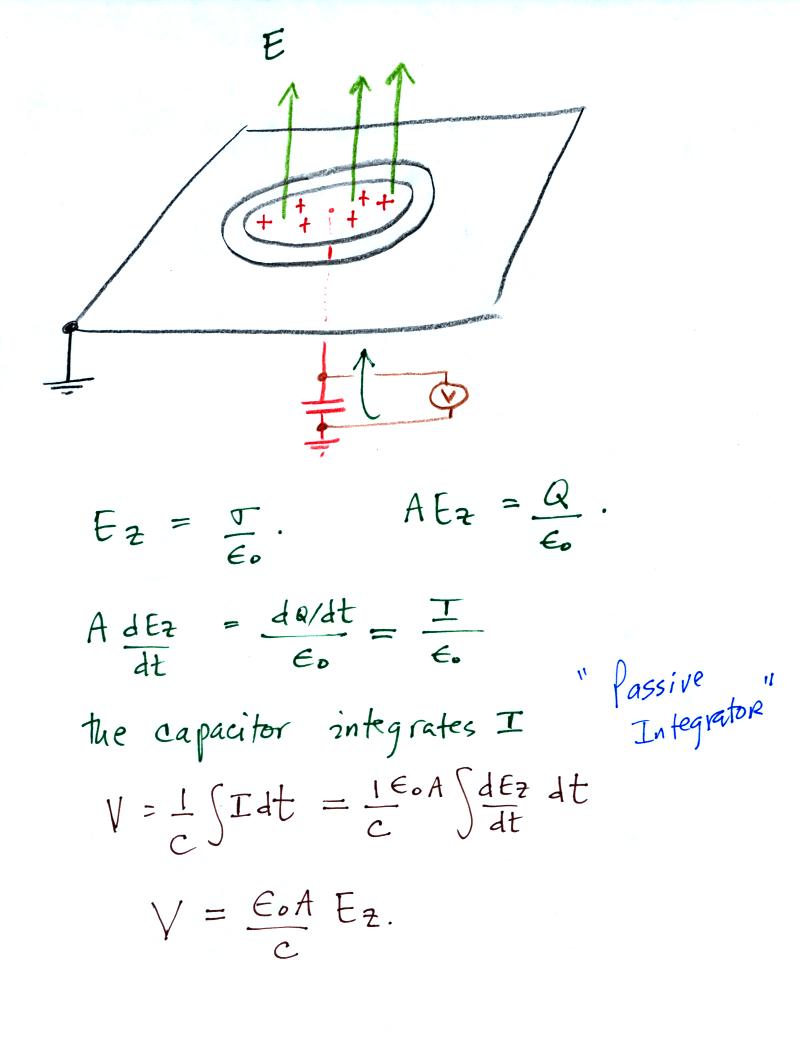
One way of
measuring time varying electric fields (from lightning discharges say)
is to use a flat plate antenna (aka flush plate dipole antenna).
It basically consists of a large flat grounded plate that would be
positioned on the ground (preferably flush with the surrounding
ground). A smaller circular sensor plate is found inside a center
hole as shown below.
Charge induced by a changing electric field moves to and from the
sensor plate. This current is proportional to the time derivative
of the electric field. Integrating the current gives an output
signal that is proportional to E.
In the circuit above the antenna is connected to a capacitor (this is a
passive integrator). Some kind of measuring device would be
connected across the capacitor.
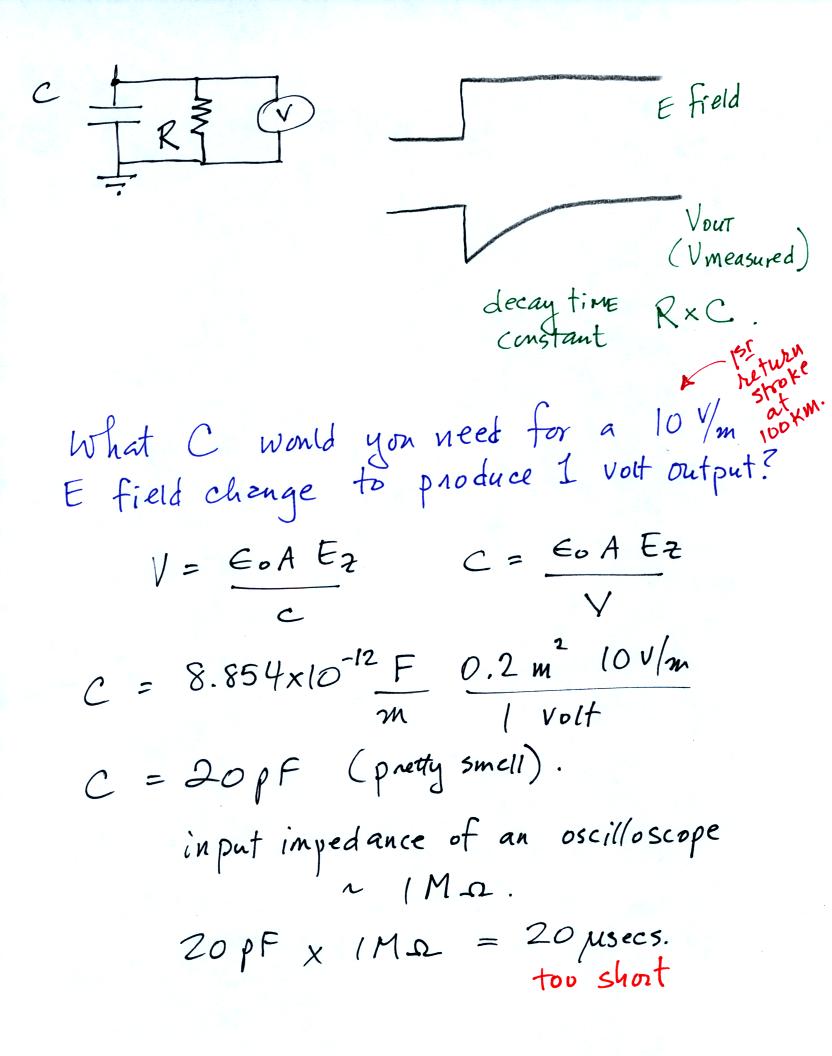
In some cases the input impedance of the measuring device together with
a small capacitance in the passive integrator (a small capacitance
would provide higher gain) gives a time decay constant that is too
short. An example is shown above.
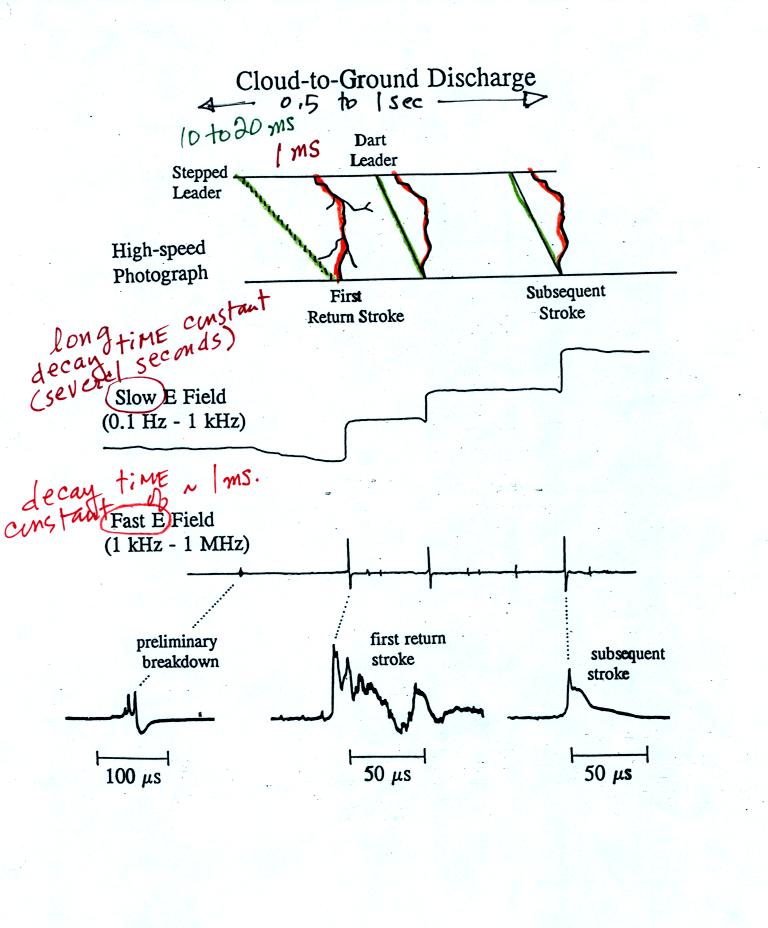
A cloud to ground discharge typically last around 0.5 seconds.
You could use a so-called "slow E field antenna" to faithfully record
the electric field changes that occur during the totality of the
flash. A slow antenna might have a time decay constant of several
seconds. If you want to study the individual return strokes, say,
you can use a "fast E field antenna" which has a much shorter
(typically about 1 ms) decay time constant.
When the E field antenna sensor plate is connected to an active
integrator circuit like shown above, the input impedance of the
measuring equipment won't affect the decay time constant. The
decay time constant is determined by the R and C values in the
operational amplifier feedback circuit.
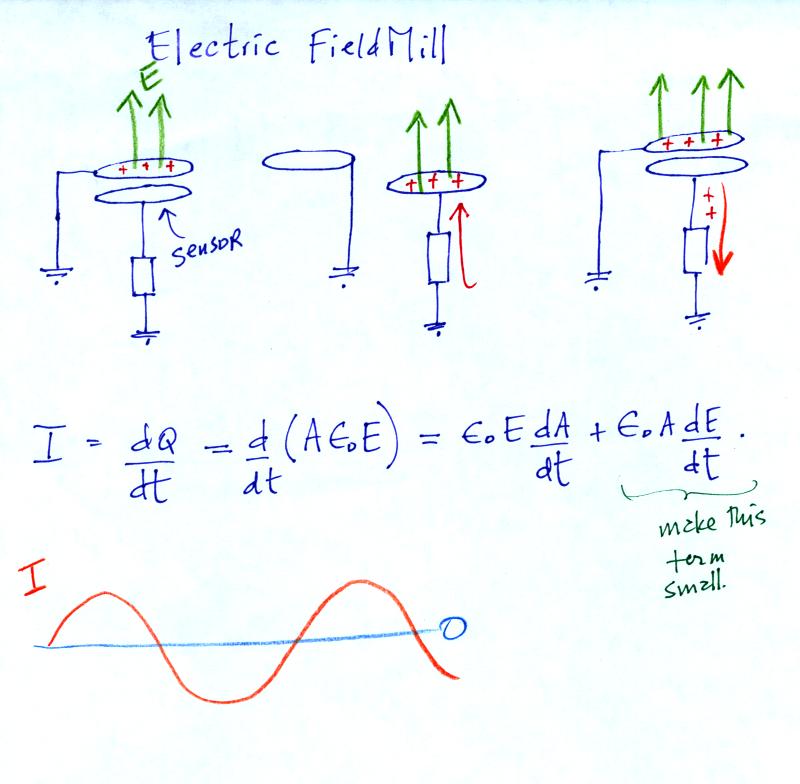
Flat plate antennas can be used to measure time varying
electric fields but not static fields. For static fields, a
"field mill" is usually used.