Fri., Jan. 31 notes

Friday Jan. 31, 2014

A couple of songs from a group from Portland, OR, that I like - Black Prairie. You heard "Dirty River Stomp" and "Nowhere Massachusetts".

The Optional Assignment and the 1S1P reports on "Scattering of Light" were collected today. It can take some time to get the 1S1P reports graded. I'll try to have the Optional Assignments graded in time to return in class on Monday. I'll also post some answers to the questions online before then.

Note that the times and locations of next week's Practice Quiz Reviews have been determined (they're listed on the class homepage and on the study guide).

A potpourri of topics today.

1. Pressure decreases with increasing altitude at a rate that depends on air density.
We didn't quite have time for this at the end of class on Wednesday but I stuck the notes onto the end of Wednesday's notes anyways. I won't reproduce them here. But I will mention that this pressure decrease dependence on air density is a fairly important point that will come up 3 or 4 more times during the semester. The fact that pressure decreases relatively slowly when moving up through low density air is part of what allows hurricanes to develop into the intense storms that they sometimes become.

2. Pressure pushes downward, upward, and sideways.

In class on Wednesday we figured out that it would take a stack of about 90 bricks, each weighing 5 lbs, to produce 15 psi pressure at the bottom of the column. I.e. about the same as what the atmosphere can do at sea level (14.7 psi is average sea level pressure).

The next time you're at the beach, that's something to think about.

Atmospheric pressure is equivalent to a 15 foot tall, 450 pound stack of bricks, weighing down on the yellow rectangle drawn on this person's chest.

Our bodies can handle 1 atmosphere of pressure. They can't cope very well with the 8 atm. of pressure that free divers find at a depth of 230 ft in the ocean.

Pressure at any level in the atmosphere depends on (is determined by) the weight of the air overhead. All this talk of piles of bricks though might leave you with the idea that pressure just pushes downward.

Air pressure is a force that pushes downward, upward, and sideways. If you fill a balloon with air and then push downward on it, you can feel the air in the balloon pushing back (pushing upward). You'd see the air in the balloon pushing sideways as well.

We were able to see this by placing a brick on top of a balloon. The balloon gets squished but not flattened. It eventually pushes back with enough force to support the brick. If I could figure out a way of keeping the balloon from moving too far sideways I could have gotten on the table and stood on the balloon. With only a little compression it would have been able to support all 150 pounds of my weight.

Another helpful representation of air in the atmosphere might be a people pyramid.

If the bottom person in the stack above were standing on a scale, the scale would measure the total weight of all the people in the pile. That's analogous to sea level pressure being determined by the weight of the all the air above.

The bottom person in the picture above must be strong enough to support the weight of all the people above. That is equivalent to the bottom layer of the atmosphere pushing upward with enough pressure to support the weight of the air above.

Here's another example of air pressure pushing upward - automobiles.

My French vehicle (a Peugeot 404) and my current automobile (a 1980 Toyota Celica).
The car sits on 4 tires, which are really nothing more than balloons. The air pressure in the four tires pushes upward with enough force to keep the 1000 or 2000 pound vehicle off the ground. The air pressure also pushes downward, you'd feel it if the car ran over your foot. The air also pushes sideways with a lot of force; tires need to be strong to keep from exploding or coming off the wheel.

3. Measuring pressure using a mercury barometer.

One of the more impressive seesaws (teeter totters) that I've seen (source of this image). If you understand how this works you'll be able to figure out how barometers function.

A mercury barometer is used to measure atmospheric pressure and is really just a balance that can be used to weigh the atmosphere. You'll find a messier version of what follows on p. 29 in the photocopied Class Notes.

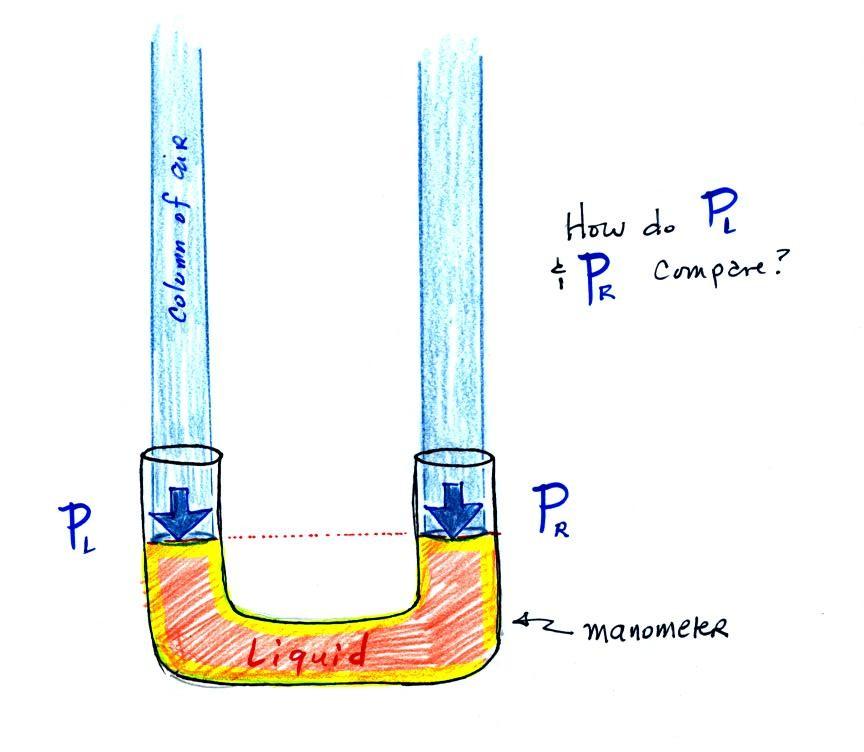
The instrument in the left figure above ( a u-shaped glass tube filled with a liquid of some kind) is actually called a manometer and can be used to measure pressure difference. The two ends of the tube are open so that air can get inside and air pressure can press on the liquid. Given that the liquid levels on the two sides of the manometer are equal, what could you say about P_L and P_R?

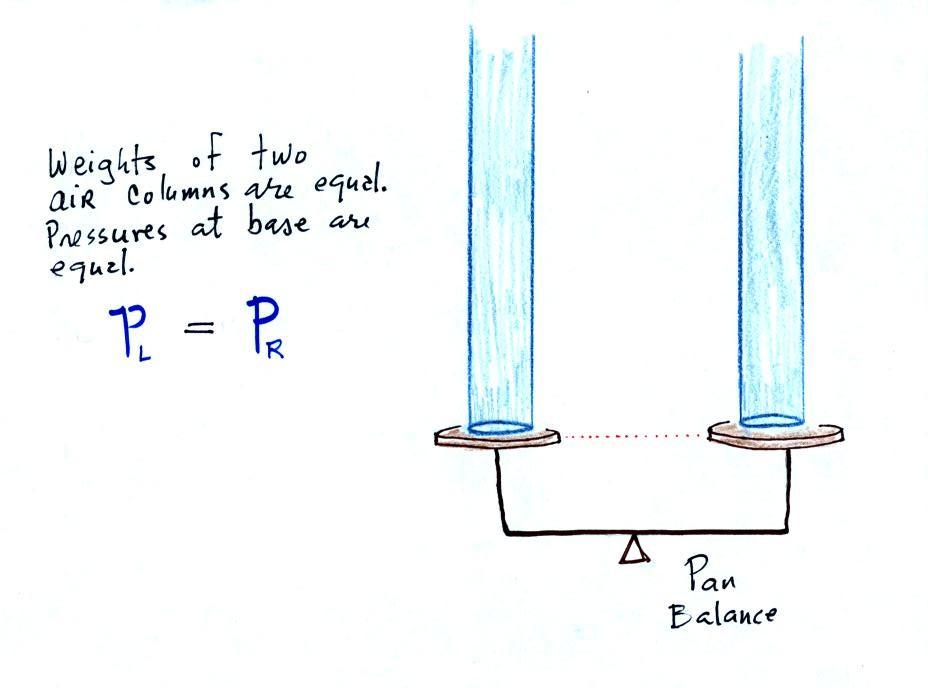
The liquid can slosh back and forth just like the pans on a balance can move up and down. A manometer really behaves just like a pan balance (pictured above at right) or a teeter totter (seesaw). Because the two pans are in balance, the two columns of air have the same weight. P_L and P_R are equal (but note that you don't really know what either pressure is, just that they are equal).

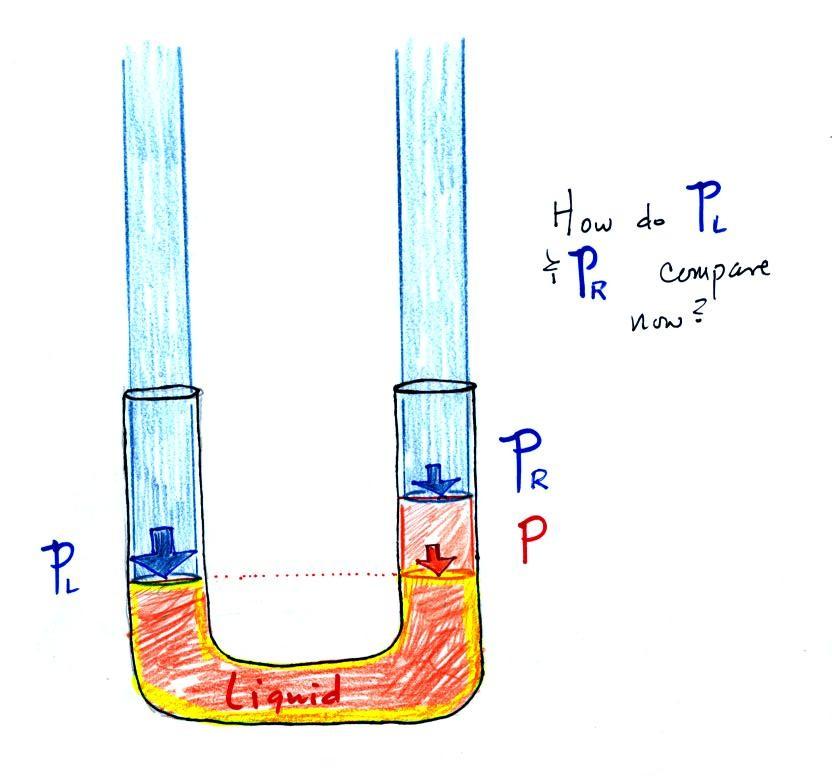
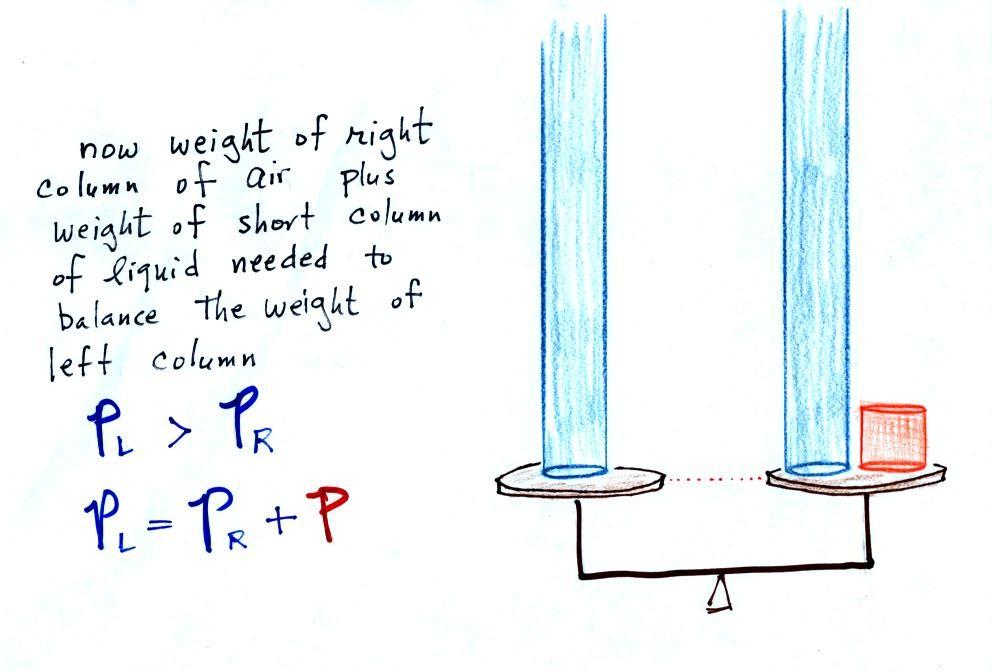
Now the situation is a little different, the liquid levels are no longer equal. You probably realize that the air pressure on the left, P_L, is a little higher than the air pressure on the right, P_R. P_L is now being balanced by P_R + P acting together. P is the pressure produced by the weight of the extra fluid on the right hand side of the manometer (the fluid that lies above the dotted line). The height of the column of extra liquid provides a measure of the difference between P_L and P_R.

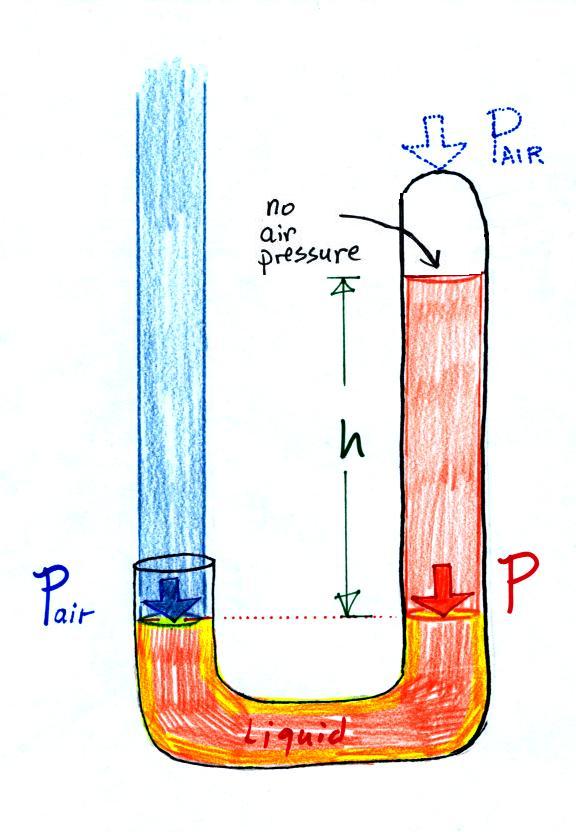
Next we will just go and close off the right hand side of the manometer.

Air pressure can't get into the right tube any more. Now at the level of the dotted line the balance is between P_air and P (pressure by the extra liquid on the right). If P_air changes, the height of the right column, h, will change. You now have a barometer, an instrument that can measure and monitor the atmospheric pressure.

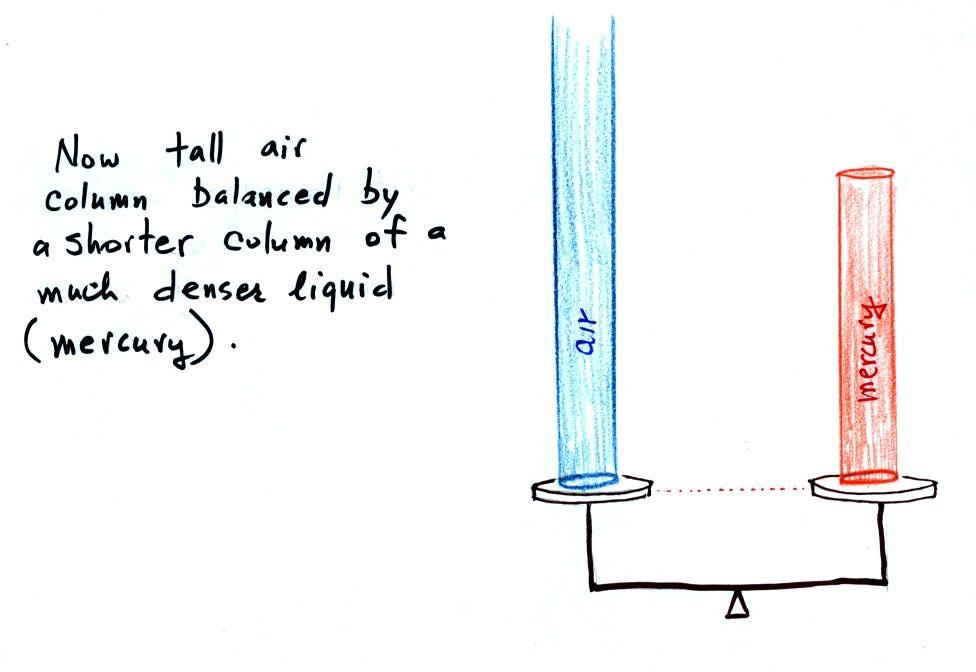
Barometers like this are usually filled with mercury. Mercury is a liquid. You need a liquid that can slosh back and forth in response to changes in air pressure. Mercury is also very dense which means the barometer won't need to be as tall as if you used something like water. A water barometer would need to be over 30 feet tall. With mercury you will need only a 30 inch tall column to balance the weight of the atmosphere at sea level under normal conditions (remember the 30 inches of mercury pressure units mentioned earlier). Mercury also has a low rate of evaporation so you don't have much mercury gas at the top of the right tube (there's some gas, it doesn't produce much pressure, but it would be hazardous you if you were to start to breath it).

Here is a more conventional barometer design. The bowl of mercury is usually covered in such a way that it can sense changes in pressure but is sealed to keep poisonous mercury vapor from filling a room.

Average sea level atmospheric pressure is about 1000 mb. The figure above (p. 30 in the photocopied Class Notes) gives 1013.25 mb but 1000 mb is close enough in this class. The actual pressure can be higher or lower than this average value and usually falls between 950 mb and 1050 mb.

The figure also includes record high and low pressure values. Record high sea level pressure values occur during cold weather. The TV weather forecast will often associate hot weather with high pressure. They are generally referring to upper level high pressure (high pressure at some level above the ground) rather than surface pressure. There is some debate about the 1085 mb pressure value measured in Mongolia. The problem is that the pressure was measured at over 5000 feet altitude and a calculation was needed to figure out what the pressure would have been if the location were at sea level. That calculation can introduce uncertainty. But you don't really need to be concerned with all that, I just wanted to give you an idea of how high sea level pressure can get.

Most of the record low pressure values have all been set by intense hurricanes (the extreme low pressure is the reason these storms are so intense). Hurricane Wilma in 2005 set a new record low sea level pressure reading for the Atlantic, 882 mb. Hurricane Katrina had a pressure of 902 mb. The following table lists some of the information on hurricane strength from p. 146a in the photocopied ClassNotes. 2005 was a very unusual year, 3 of the 10 strongest N. Atlantic hurricanes ever occurred in 2005.

Most Intense North Atlantic Hurricanes	Most Intense Hurricanes to hit the US Mainland
Wilma (2005) 882 mb Gilbert (1988) 888 mb 1935 Labor Day 892 mb Rita (2005) 895 mb Allen (1980) 899 Katrina (2005) 902	1935 Labor Day 892 mb Camille (1969) 909 mb Katrina (2005) 920 mb Andrew (1992) 922 mb 1886 Indianola (Tx) 925 mb

Note that a new all time record low sea level pressure was measured in 2003 inside a strong tornado in Manchester, South Dakota (F4 refers to the Fujita scale rating, F5 is the highest level on the scale). This is very difficult (and very dangerous) thing to try to do. Not only must the instruments be built to survive a tornado but they must also be placed on the ground ahead of an approaching tornado and the tornado must then pass over the instruments (also the person placing the instrument needs to get out of the way of the approaching tornado).

You can experience much larger changes in pressure if you move vertically in the atmosphere than you would ever be able to do at sea level. Pressure in Tucson at 2500 feet altitude is routinely about 920 mb; it's even lower, about 700 mb, at the top of Mt. Lemmon. The only place to experience 920 mb pressure at sea level would be in the middle of a strong hurricane. Pressure never drops to 700 mb at sea level.

4. A pressure force demonstration I'd like to do and one that I can (and will do)

Here's a description of the demonstration I'd like to try, it involves Magdeburg hemispheres and two teams of horses (the following quote and the figure below are from an article in Wikipedia):

" ... Magdeburg hemispheres are a pair of large copper hemispheres with mating rims, used to demonstrate the power of atmospheric pressure. When the rims were sealed with grease and the air was pumped out, the sphere contained a vacuum and could not be pulled apart by teams of horses. The Magdeburg hemispheres were designed by a German scientist and mayor of Magdeburg, , Otto von Guericke in 1656 to demonstrate the air pump which he had invented, and the concept of atmospheric pressure."

Gaspar Schott's sketch of Otto von Guericke's Magdeburg hemispheres experiment (from the Wikipedia article referenced above)

It is the pressure of the air pushing inward against the outside surfaces of the hemispheres that keeps them together. The hemispheres appear to have had pretty large surface area. There would be 15 pounds of force pressing against every square inch (at sea level) of the hemisphere which could easily have been several thousand pounds of total force.

Suction cups work the same way

Air pressure outside the suction cup (caused by the collisions of air molecules) press the suction cup against a smooth surface. There no (or very little) air inside the suction cup and no pressure pushing outward. The suction cup is held against the surface (with a fair amount of force).

Here's a substitute demonstration.
A demonstration that tries to prove that air pressure really does push upward as well as downward. Not only that but that the upward force is fairly strong. The demonstration is summarized on p. 35a in the ClassNotes.

It's pretty obvious that if you fill a balloon with a little water and let go it will fall. Gravity is responsible but there is a little more to the problem than you might first imagine.

Here's a little bit more detailed and more complete explanation of what is going on.

The figure at left shows air pressure (red arrows) pushing on all the sides of the balloon. Don't worry about the numbers, I just made them up.

The two sideways forces (14.5 units of force) are equal and opposite and cancel each other out.

Because pressure decreases with increasing altitude, the pressure from the air at the top of the balloon pushing downward (strength=14) is a little weaker than the pressure from the air at the bottom of the balloon that is pushing upward (strength=15).

The total effect of the pressure is a weak upward pressure difference force (1 unit of upward force shown at the top of the right figure).

Gravity exerts a downward force on the water balloon. In the figure at right you can see that the gravity force (strength=10) is stronger than the upward pressure difference force (strength=1). The balloon falls as a result.

In the demonstration a wine glass is filled with water (about the same amount of water that you might put in a small water balloon).

A small plastic lid is used to cover the wine glass (you'll need to look hard to see the lid in the photo above). The wine glass is then turned upside and the water does not fall out.

All the same forces are shown again in the left most figure. In the right two figures we separate this into two parts - a water and lid part and an empty glass part. First the water inside the glass isn't feeling the downward and sideways pressure forces because they're pushing on the glass and I was holding onto the glass.

Gravity still pulls downward on the water with the same 10 units of force. But the upward pressure force is able to overcome the downward pull of gravity. It can do this because all 15 units are used to overcome gravity and not to cancel out the downward pointing pressure force. The net upward force is strong enough to keep the water in the glass.

The demonstration was repeated using a 4 Liter flash (more than a gallon of water, more than 8 pounds of water). The upward pressure force was still able to keep the water in the flask (much of the weight of the water is pushing against the sides of the flask which the instructor was supporting with his arms).

5. Air density changes with increasing altitude

We didn't actually have time for this last topic and it wasn't discussed in class. But I've included some notes any way. We'll come back to this probably next Friday, after the Practice Quiz.

We've spent a lot of time looking at air pressure and how it changes with altitude. Next we'll consider air density and later air temperature.

How does air density change with increasing altitude? You should know the answer to that question. You get out of breath more easily at high altitude than at sea level. Air gets thinner (less dense) at higher altitude. A lungful of air at high altitude just doesn't contain as much oxygen as at lower altitude or at sea level.

We've used bricks to try to understand that air pressure depends on the weight of the air overhead and that it decreases with increasing altitude. Because air is compressible, a stack of mattresses might be a more realistic representation of layers of air than a pile of bricks.

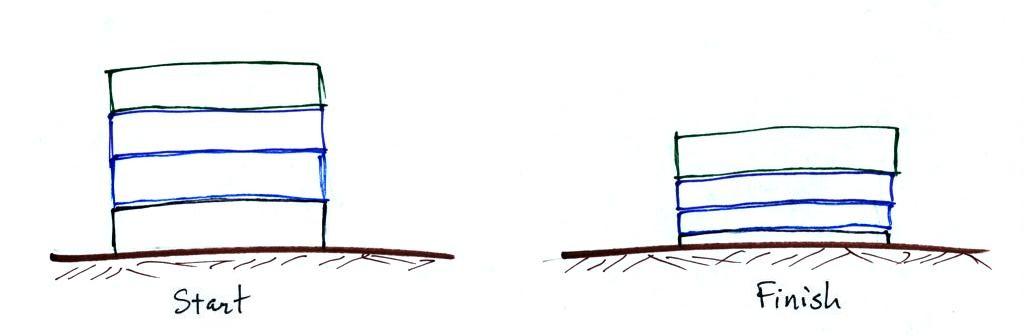
Four mattresses are stacked on top of each other. Mattresses are reasonably heavy, the mattress at the bottom of the pile is compressed by the weight of the three mattresses above. This is shown at right. The mattresses higher up aren't squished as much because their is less weight remaining above. The same is true with layers of air in the atmosphere.

The statement above is at the top of p. 34 in the photocopied ClassNotes. I've redrawn the figure found at the bottom of p. 34 below.

There's a surprising amount of information in this figure that you'd miss if you don't spend a minute or two looking for it and thinking about it.

1. You can first notice and remember that pressure decreases with increasing altitude. 1000 mb at the bottom decreases to 700 mb at the top of the picture. You should be able to explain why this happens.

2. Each layer of air contain the same amount (mass) of air. This is a fairly subtle point. You can tell because the pressure drops by 100 mb as you move upward through each layer. Pressure depends on weight. So if all the pressure changes are equal, the weights of each of the layers must be the same. Each of the layers must contain the same amount (mass) of air (each layer contains 10% of the air in the atmosphere).

3. The densest air is found at the bottom of the picture. The bottom layer is compressed the most because it is supporting the weight of all of the rest of the atmosphere. It is the thinnest layer in the picture and the layer with the smallest volume. Since each layer has the same amount of air (same mass) and the bottom layer has the smallest volume it must have the highest density. The top layer has the same amount of air but about twice the volume. It therefore has a lower density (half the density of the air at sea level). Density is decreasing with increasing altitude. This is the main point illustrated in the figure.

4. Finally pressure is decreasing most rapidly with increasing altitude in the densest air in the bottom layer. This is what we covered at the beginning of class though it's illustrated a little differently here.