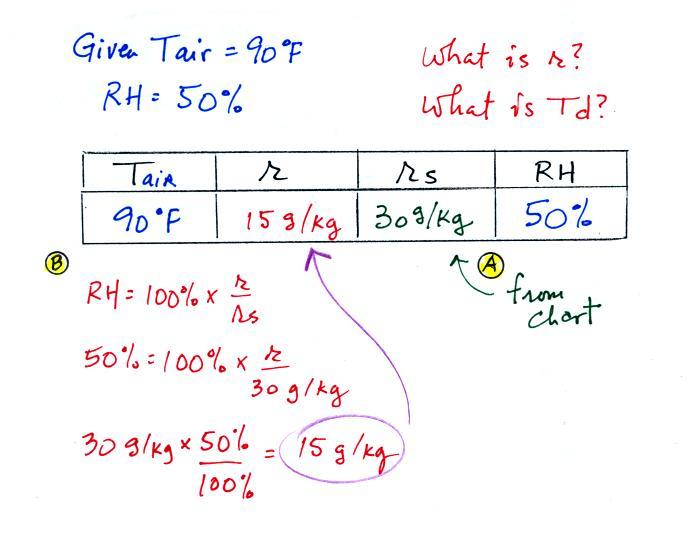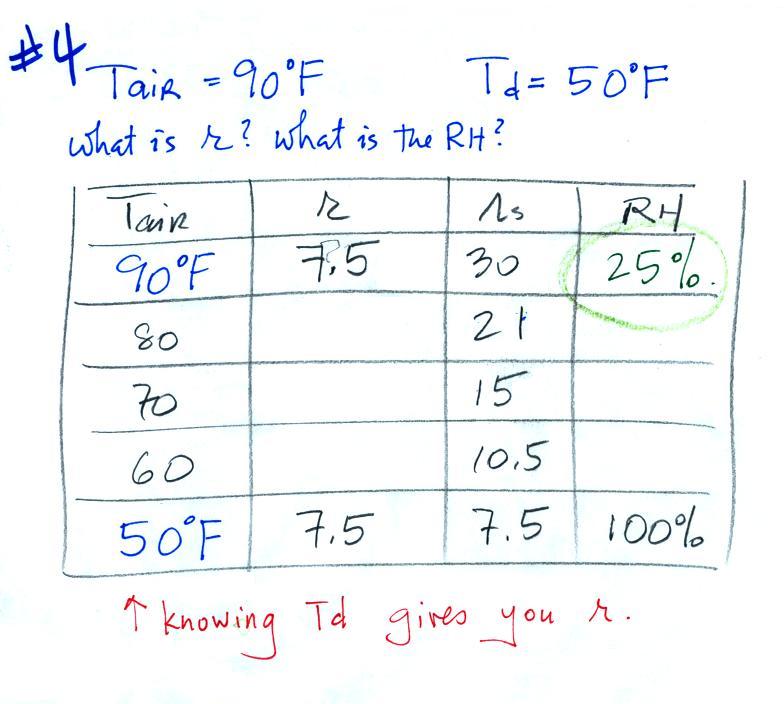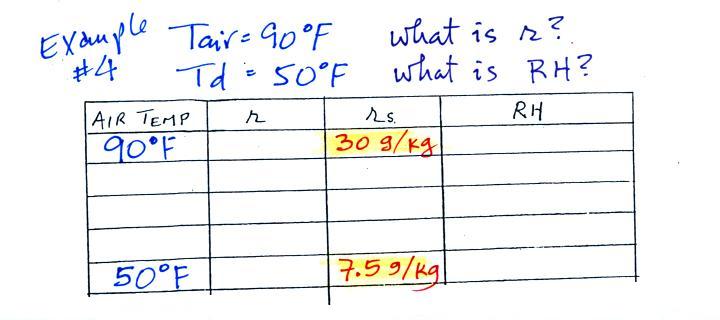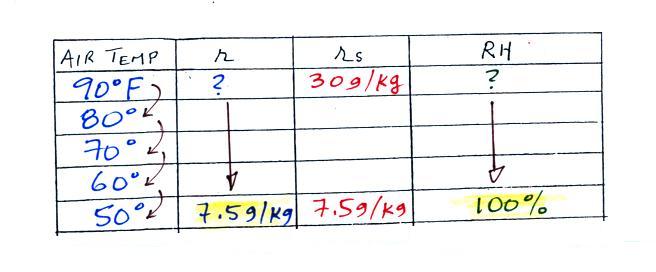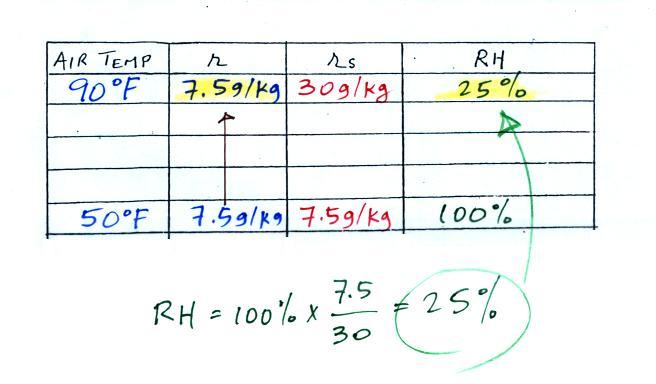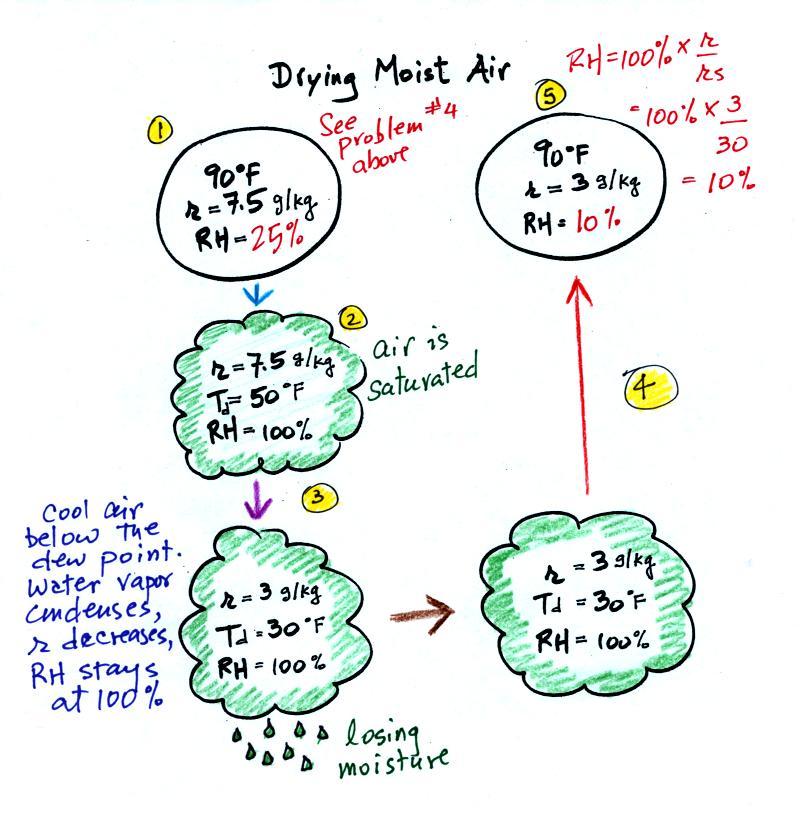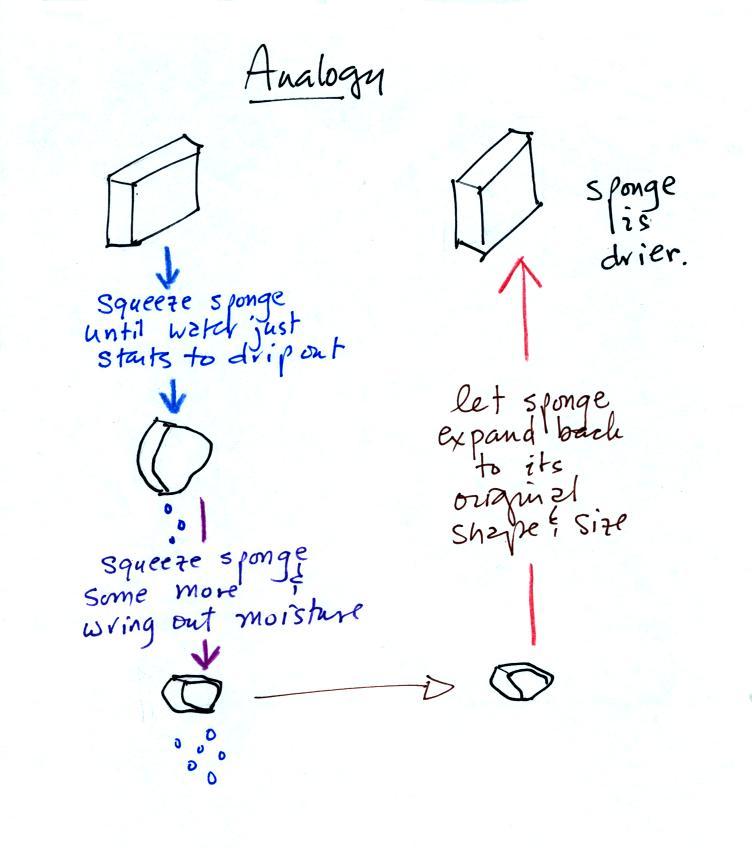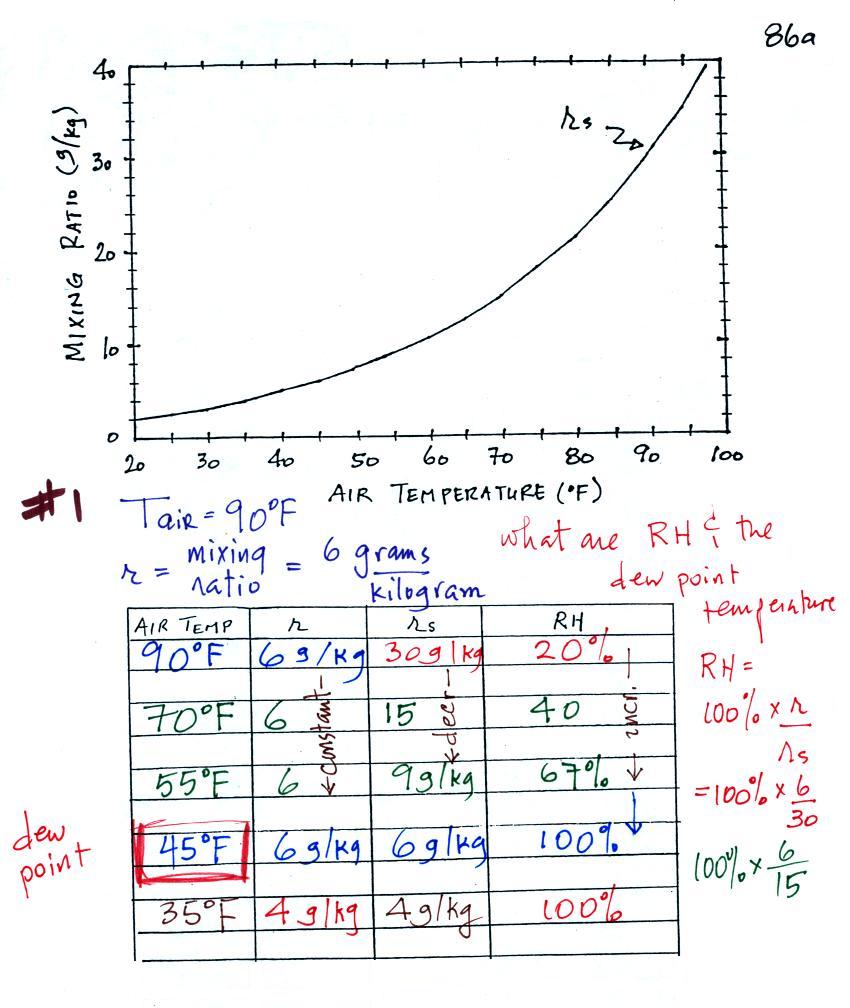
| humidity variable |
mixing ratio |
saturation
mixing ratio |
relative
humidity |
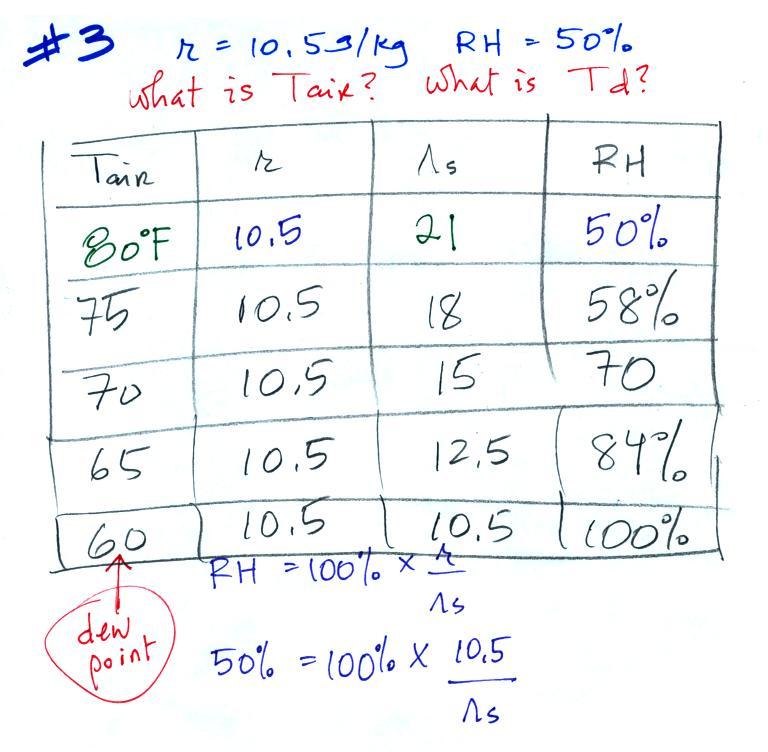
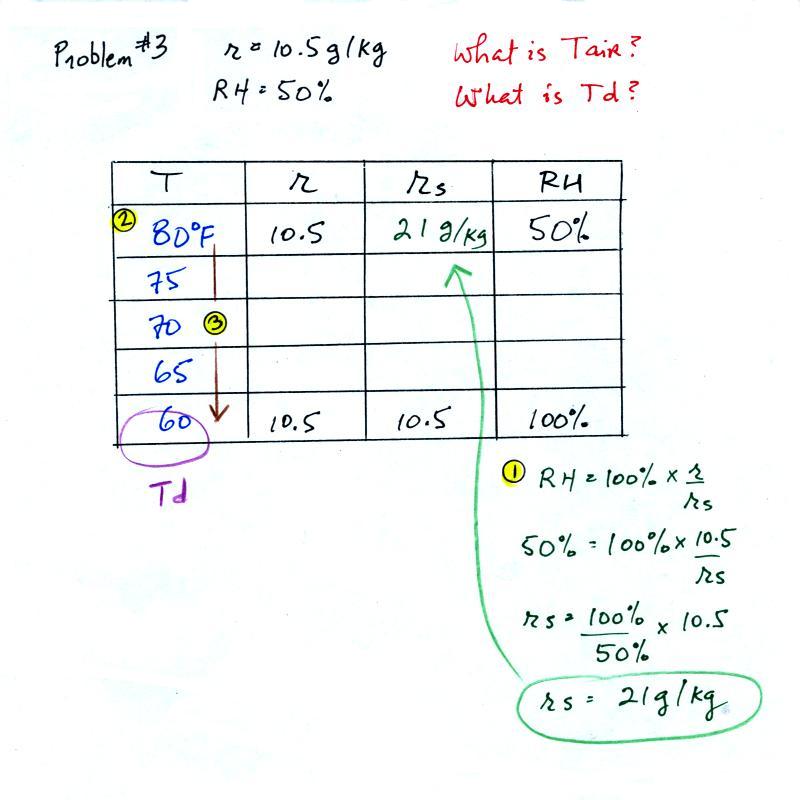
dew point
temperature |
| "job" |
how much water vapor is actually
in the air |
the maximum amount of water
vapor that can be found in air |
how close is the air to being filled to
capacity with water vapor |
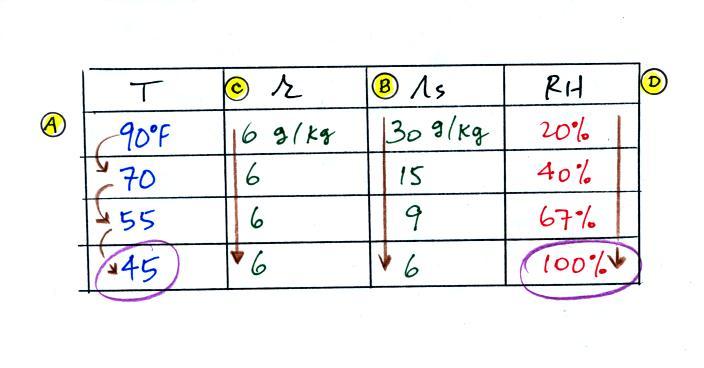
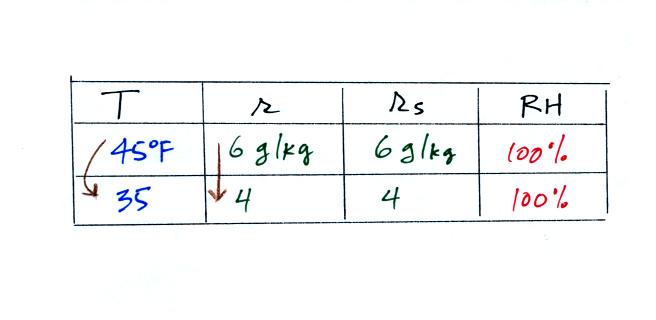
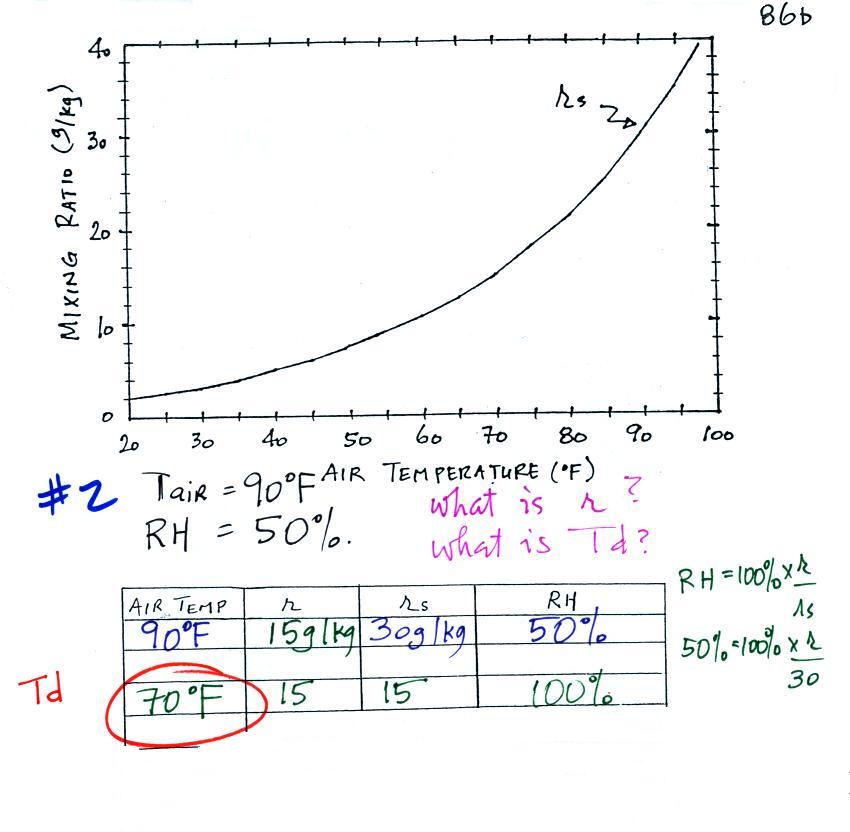
1. like mixing ratio it gives an idea of
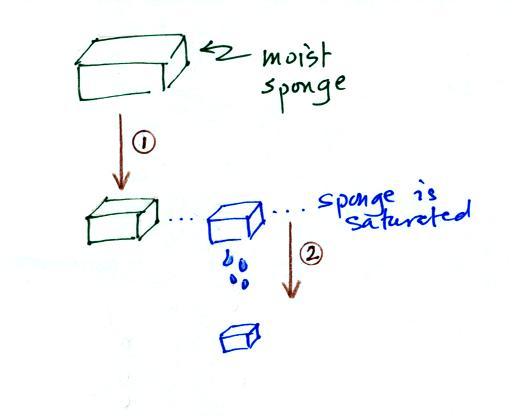
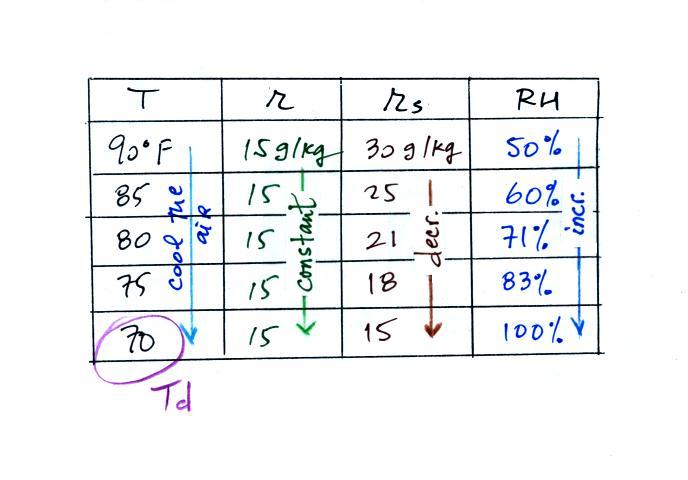
the actual amount of water vapor in the air 2. cool the air to its dew point and RH becomes 100% |
| units |
g/kg |
g/kg |
% |
oF |
| when and why do the values of these
variables change? |
this is
what we'll be working on today
|
|||