Friday Feb. 19, 2016
Roy Orbison from the Black and White Night Concert: "Claudette"
(3:11), "Uptown"
(3:20), "Candy
Man" (3:26), "Pretty Woman"
(6:18)
We were able to get the Sect. 1 quizzes graded in time to
return in class today but not the quizzes from the 1 pm
class. We'll have them by Monday. Next time we'll
grade your quizzes first and the other class will have to wait
until Monday (though next time will be the Friday before
Spring Break so there may not be too many people in class).
All of the Experiment #1 reports (and 1
Scientific Paper report) have been graded, including the ones
turned in earlier this week. You can revise your
experiment (and Scientific Paper) reports if you want to (a
revision is not required). Unless noted otherwise (on
your report) revised reports are due by Wed., Mar. 2.
Please return the original report with your revised report.
There are a couple of Assignments due next week. See the
class homepage for more details.
There were network problems
somewhere on campus so the class webpage wasn't available
during class. That made things a little
more chaotic and confusing than normal, you'll want to be sure to read through the
online notes that follow. Everything was
working fine by the time I got back to my office of course,
that's how events like this work.
It's a lucky thing we don't use a textbook in this
class. If we did we would just be moving into Chapter
2. During the next couple of weeks we will be concerned with
energy, temperature, heat, and energy transport. We'll look
at the flow of energy back and forth between the earth's surface
and it's atmosphere; the greenhouse effect is a big part of that.
It is easy to lose sight of the main concepts because all the
details. The following is an introduction to this new
section of material and most of the figures are found on pages
43 & 44 in the photocopied ClassNotes.
It might be helpful also to keep a list of the various topics as
we cover them in class today. I've included an example
list at the end of today's notes.
1. Types of energy
Kinetic energy is
energy of motion. Some examples (both large and
microscopic scale) are mentioned and sketched above.
This is a relatively easy to visualize and understand form
of energy.
Radiant energy is a very important form of
energy that was somehow left off the original list in the
ClassNotes . Electromagnetic radiation is
another name for radiant energy. Sunlight is an example of
radiant energy. It's something that we can see and feel (you
feel warm when you stand in sunlight). Something that is not
quite so obvious is that everyone in the classroom is emitting
radiant energy. This is infrared light, an invisible form of
radiant energy. And actually it's not just the people; the
walls, ceiling, floor and even the air in the classroom are also
emitting infrared light. We can't see it. Because it's
there all the time I'm not sure whether we can feel it or not.
Latent heat energy is an, important,
under-appreciated, and rather confusing type of
energy. The word latent refers to energy that is
hidden. That's part of the problem. Another
part of what makes latent heat energy hard to visualize
and appreciate is that the energy is hidden or stored in
water vapor or water - that seems an unlikely place to
find energy.
It might be helpful to think of latent heat energy as
being a form of potential energy.
Gravitation potential energy is
something I suspect you're familiar with.
|

|

|
It would take a lot of energy to push a
rock up a hill.
|
Once at the top of the hill the rock has
a lot of stored, potential energy (the energy that it took
to get it there).
|
This energy would reappear as kinetic
energy if you were to push the rock and start it rolling
down hill. |
Energy is being added in the left figure, stored
energy is shown in the middle figure, and the energy
reemerges or is released in the final picture.
Latent heat energy
|

|
|
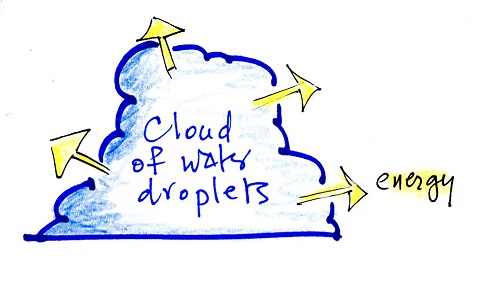
Some of the sunlight energy
hitting water warms the water.
The rest is used to evaporate water.
|
The water vapor contains a lot of
stored, "latent heat", energy (sunlight energy that was
added during evaporation).
|
The stored energy is released when the
water vapor condenses and turns back into water.
|
The same kind of scenario is shown
here except that it involves water, water vapor, and
sunlight. Energy is added in the left figure and is used to
evaporate some water. The added energy is stored or hidden
in the water vapor, and the energy is released when the water
vapor condenses and turns back into water. It
takes a lot of energy to evaporate water.
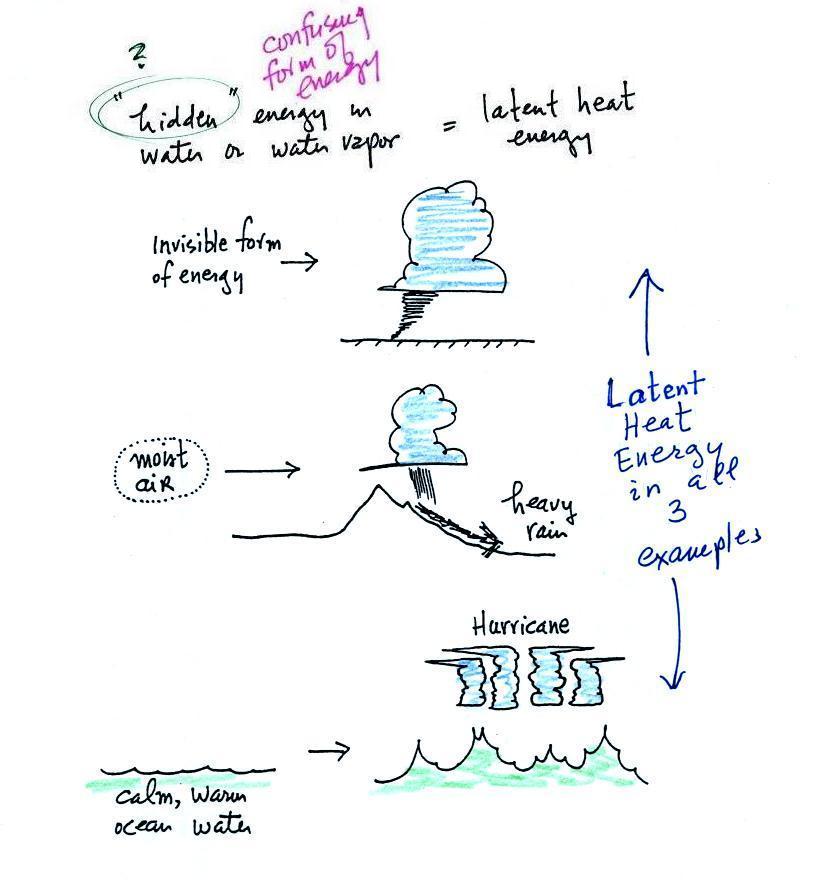
Here are three examples showing
energy originally hidden in water vapor reemerging in a
tornado, water rushing down a mountain or wash, and a
hurricane. A big part of the energy in the tornado,
flash flood, and hurricane was initially hidden in the
water vapor.
2. Energy units
Next just brief mention of units of energy

Joules
are the units of energy that you would probably
encounter in a physics class. Your
electric bill shows the amount of energy that
you have used in a month's time, the units are
kilowatt-hours.
We'll usually be using calories as units of
energy. 1 calorie is the energy need to warm 1
gram of water 1 C (there are about 5 grams of water in
a teaspoon).
Here's a little miscellaneous information that you
don't need to worry about remembering. You've
probably seen the caloric content of food on food packages
or on menus in restaurants. 1 "food calorie" is
actually 1000 of the calories mentioned above (food is
probably a form of chemical energy, the energy is released
when the food is consumed).

A 150 pound person would burn
almost 500 food calories while sleeping during the
night (8 hours x 60 minutes per hour x 1 food
calorie per minute). This is about the energy
contained in one donut.
3. Energy transport processes
By far the most important process is at
the bottom of the list above. Energy transport in the
form of electromagnetic radiation (sunlight for example) is
the only process that can transport energy through empty
space. Electromagnetic radiation travels both to the
earth (from the sun) and away from the earth back into
space. Electromagnetic radiation is also responsible
for about 80% of the energy transported between
the ground and atmosphere.
You might be surprised to learn that latent heat is the
second most important transport process. This term
latent heat can refer to both a type of energy and an energy
transport process (the energy is hidden in the water vapor,
the water vapor can move around and carry that energy with
it).
Rising parcels of warm air and sinking parcels of cold
air are examples of free convection. Because of
convection you feel colder or a cold windy day than on a
cold calm day (the wind chill effect). Ocean
currents are also an example of convection.
Convection is also one of the ways of rising air motions
in the atmosphere (convergence into centers of low pressure
and fronts are two other ways we've encountered so
far)
Conduction is the least important energy transport at
least in the atmosphere. Air is such a poor conductor
of energy that it is generally considered to be an
insulator.
4. Energy balance
The next picture (the figure in
the ClassNotes has been split into three parts for improved
clarity) shows energy being transported from the sun to the
earth in the form of electromagnetic radiation. On average
about half of this sunlight passes through the atmosphere and is
absorbed at the ground. This causes the ground to warm
(sunlight energy striking the ocean warms the oceans but is also
used to evaporate ocean water). Measuring the
energy in sunlight arriving at the surface of the earth is the
object of Experiment #3.
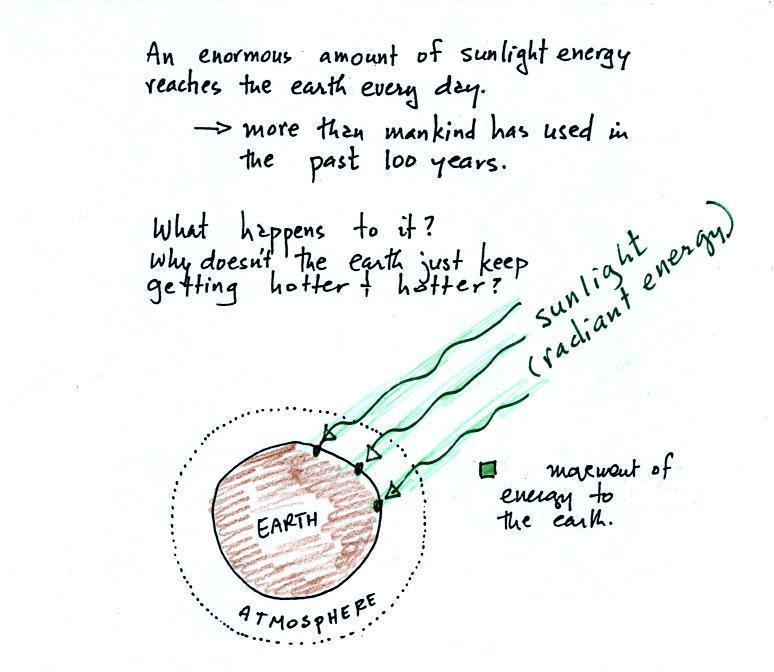
We are aware of this energy
because we can see it (sunlight also contains invisible
forms of light) and feel it. With all of this
energy arriving at and being absorbed by the earth, what
keeps the earth from getting hotter and hotter? If
you park your car in the sun it will heat up. But
there is a limit to how hot it will get. Why is
that?
It might be helpful
when talking about energy balance to think of a bank
account. You open a bank account and start
depositing money. The bank account balance starts to
grow. But it doesn't just grow without limit.
Why not? The answer is that once you find money in
the bank you start to spend it. The same is true of
energy and the earth. Once the earth starts to warm
it also starts to emit energy back into space (the orange
arrows in the figure below). Radiant energy is
emitted by the ground, the oceans, and the
atmosphere.
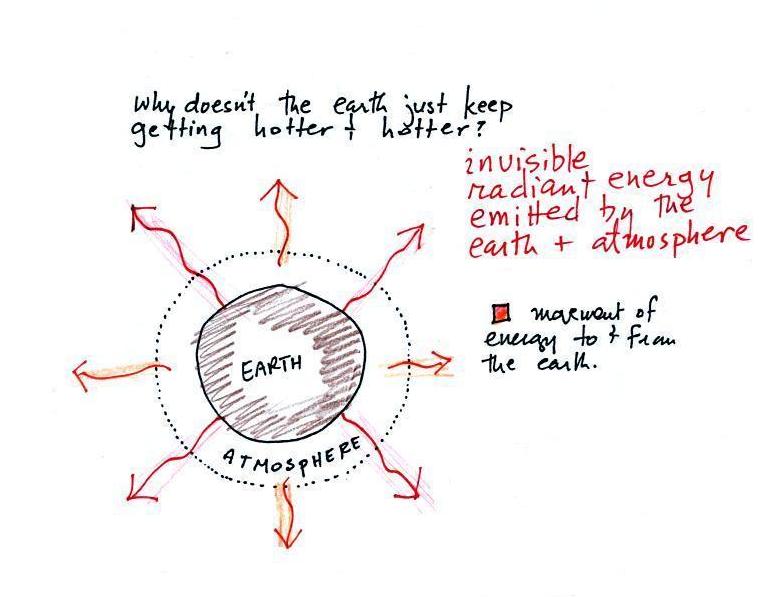
Energy is emitted by the earth in the form of infrared light,
an invisible form of energy (to human eyes anyways). A
balance between incoming and outgoing energy is achieved and the
earth's annual average temperature remains constant.
We will also look closely at energy transport between the
earth's surface and the atmosphere (see the figure below). This
is where latent heat energy transport, convection and conduction
operate (they can't transport energy beyond the atmosphere and
into outer space).
This is also where we
will find the atmospheric greenhouse. That
will be a important goal - to better understand how
the atmospheric greenhouse effect works.
5. The atmospheric greenhouse effect

The greenhouse effect is getting a lot of
"bad press". If the earth's atmosphere didn't contain
greenhouse gases and if there weren't a greenhouse effect,
the global annual average surface temperature would be about
0 F (scratch out -4 F in the figure above and put 0 F, it's
easier to remember). Greenhouse gases raise this
average to about 60 F and make the earth a much more
habitable place. That is the beneficial side of the
greenhouse effect. That's mostly what we'll be
concentrating on - how can the greenhouse effect cause this
warming, how can it produce this much warming.
The detrimental side is that atmospheric greenhouse gas
concentrations are increasing (no real debate about
that). This might enhance or strengthen the greenhouse
effect and cause the earth to warm (some debate here
particularly about how much warming there might be).
While that doesn't necessarily sound bad it could have many
unpleasant side effects (lots of debate and uncertainty
about this). That's a subject we'll explore at various
times during the semester.
6. Energy, temperature, and specific heat
(p. 45 in the ClassNotes)
When you add energy to an object, the object will usually warm
up (or if you take energy from an object the object will
cool). It is relatively easy to come up with an equation
that allows you to figure out what the temperature change will be
(this is another equation I'll try to remember to write on the
board before the next quiz - try to understand it, you don't
have to memorize it).
The temperature change, ΔT, will first depend on how much
energy was added, ΔE. This is a
direct proportionality, so ΔE is in the
numerator of the equation (ΔE and ΔT
are both positive when energy is added, negative when energy is
removed)
When you add equal amounts of energy to large and small pans of
water, the water in the small pan will get hotter. The
temperature change, ΔT, will depend on the
amount of water, the mass. A small mass will mean a large ΔT,
so mass should go in the denominator of the equation.
Specific heat is what we use to account for the fact that
different materials react differently when energy is added to
them. A material with a large specific heat will warm more
slowly than a material with a small specific heat. Specific
heat has the same kind of effect on ΔT as
mass. Specific heat is sometimes called "thermal mass" or
"thermal capacity." You can think of specific
heat as being thermal inertia - a substance with high specific
heat, lots of thermal inertia, will be reluctant to change
temperature.
Here's an important example that will show the effect of
specific heat (middle of p. 45).
Equal amounts of energy (500 calories) are added to
equal masses (100 grams) of water and soil. We use water and
soil in the example because most of the earth's surface is either
ocean or land. Before we do the calculation, try to guess which
material will warm up the most. Everything is the same
except for the specific heats. Will water with its 4 times
larger specific heat warm up more or less than the soil?
The details of the calculation are shown below.

With its higher specific heat, the water
doesn't heat up nearly as much as the soil. If we had
been removing energy the wouldn't cool off as much as the soil
would.
7. Water moderates climate
These different rates of warming of water and soil have important
effects on regional climate.
Oceans moderate the climate. Cities near a large body of
water won't warm as much in the summer and won't cool as much
during the winter compared to a city that is surrounded by land.
Water's ΔT is smaller than land's because water has
a higher specific heat.
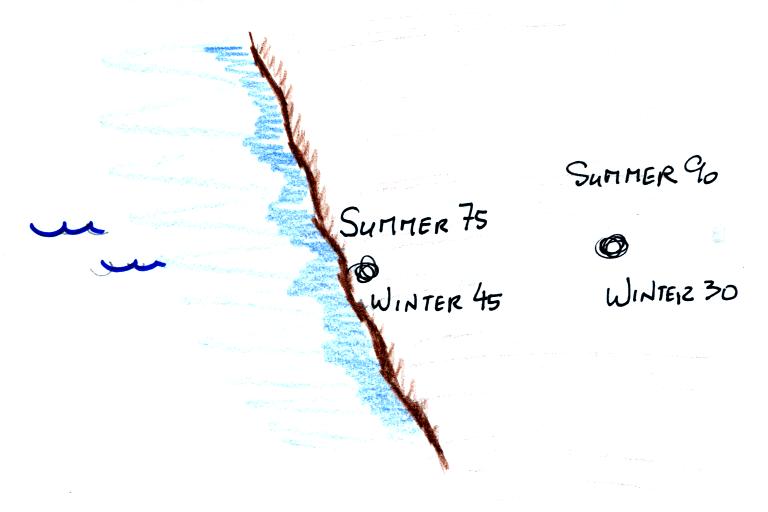
The yearly high and low monthly average temperatures are shown
at two locations above. The city on the coast has a 30o
F annual range of temperature (range is the difference
between the summer and winter temperatures). The city
further inland (assumed to be at the same latitude and altitude)
has an annual range of 60o F. Note that
both cities have the same 60o F annual average
temperature.
Water moderates climates - it reduces the difference between
summertime high and wintertime low temperatures.
Growing tomatoes in the desert -
practical application
Here's another situation where you can take
advantage of water's high specific heat to moderate climate on a
smaller scale.
You need to start tomatoes early
in Tucson (mid February) before it gets too hot, so that they
can produce fruit before it gets to hot. In you need to
protect the plants from frost.
Here's one way of doing that. You
moderate the climate and surround each plant with a "wall o
water" - a teepee like arrangement that surrounds each
plant. The cylinders are filled with water and they take
advantage of the high specific heat of water and won't cool as
much as the air or soil would during a cold night. The walls
of water produce a warm moist micro climate that the tomato
seedlings love. The plastic is transparent so plenty of
sunlight can get through.
Adding energy to something will usually cause its
temperature to change. But not always. What
else could happen?
You put a pan of water on the stove and turn on the
burner. The water will warm. It will only warm to
a certain point however. Then what happens?
8. Phase changes
Sometimes when you add energy to a material it will
stop warming and will change phase. Water will warm to
212 F (100 C) and then it will start to boil. Adding
energy to ice will first warm the ice to 0 C. But then
it will stop warming and will start to turn to melt. The
dry ice above is sublimating (changing directly from solid to
gas).
It is very easy to calculate how much energy is needed to
cause a phase change.
The energy needed depends on the amount of material present
(the mass) and on the material itself (that's the Latent Heat term
above). It also depends on the specific phase change.
I.e. there are different Latent Heat values depending on whether
the material changes from solid to liquid, liquid to gas, or solid
to gas.
Measuring the latent heat of vaporization (evaporation)
of liquid nitrogen
I'm hoping we'll have enough time to conduct an
experiment.
Here's the object of the experiment:
Students working on Experiment #2 are doing something like
this, they are measuring the latent heat of fusion of ice (the
energy needed to melt ice).
The source of energy in our experiment will be the energy
contained in a cup of room temperature water. We'll
pour some liquid nitrogen into the cup of water.
Energy will naturally flow from hot (the water) to
cold (the liquid nitrogen). As energy is taken from the
water it will cool. We'll assume that all of the energy
taken from the water is used to evaporate nitrogen, no energy
flows from the cup into the surrounding air (that's part of the
reason we conduct the experiment in a Styrofoam cup.
Our earlier equation is shown above at
left. If you know how much energy is added to something
you could determine the temperature change that would
result. We can turn the equation around so that is we
measure the temperature change that any object undergoes we
can calculate the amount of energy added or removed (the
equation at right).
Here we put everything together. We'll
determine how much energy is taken from the water.
Then we'll assume all of that energy is used to evaporate
nitrogen. That's the right hand equation above.
The numbers below should be the same ones that were
collected in class today.
We start with a medium size Styrofoam cup filled about 1/3
full with room temperature water.
The cup and the water together
weighed 168.0 g of room temperature water. The cup
weighed 3.9 g, so we really had 164.1 g of water.
The water's temperature was 21.0 C.
Next we poured some liquid nitrogen into
a second, smaller styrofoam cup.
We're going to evaporate 32.3 grams of
liquid nitrogen. The total amount of energy needed to do
that, ΔE, is the mass of the liquid nitrogen times
the Latent Heat of
vaporization of Nitrogen (LHvap).
ΔE = mass x LHvap
LHvap is the energy needed per gram to vaporize
(evaporate) liquid nitrogen. That's the quantity we are
trying to measure.
We poured the 30 grams of liquid nitrogen into the cup
containing 148.2 g of water. Energy flows naturally from
hot to cold. We assume that any energy lost by the water
is used to evaporate nitrogen.
Once the liquid nitrogen was gone (it had evaporated) we
remeasured the water temperature. It had dropped to 8.5 C.
Now we're ready to calculate the latent heat of vaporization
We'll plug in all our measurements and solve for LHvap.
We set up an energy balance equation (energy lost by the
water = energy used to evaporate nitrogen) and plugged in all
our measured values. We obtained a measured value of LHvap
= 55.9 calories/gram (53 cal/g later in the day in the 11 am
class). A student in the class informed us that the known
value is 48 cal/g. Not too a bad result at all.
Here's a list of the topics that were covered in class today