A closer look at evaporation and condensation

In order to describe the physics of these processes, we need some way to specify the water vapor content of the atmosphere. There are many ways to do this and we will use a few of them in this class. The first is something called vapor pressure.

Vapor pressure (e) is the gas pressure (force/area) exerted by water vapor molecules alone. The higher the concentration of water vapor molecules (number density), the higher the vapor pressure. The average air pressure at sea level is about 1013 millibars (mb). If the total air pressure is 1013 mb and water vapor makes up 1% of the air molecules, then the vapor pressure is 1% of 1013 mb or 10.13 mb. Water vapor is a trace gas in the atmosphere of Earth -- the maximum vapor pressure is never more than about 40 mb. For now the important concept is that vapor pressure is one way to keep track of the amount of the gas water vapor. For our purposes, the higher the vapor pressure, the greater the amount of water vapor in the air.

Evaporation and condensation in a closed system

A Physical Explanation of the Processes of Evaporation and Condensation and the concept of Saturation, are depicted in this figure depicting the relationship between vapor pressure and saturation. [The figure should open in a new tab. It does not fit well on this page with the text. Click on the image to zoom.] The figure shows what happens in a "closed system." In this context a closed system means that no air or water vapor on the inside can leave the flask and no air or water vapor from outside can enter the flask. In the closed system experiment, there is a laboratory flask partially filled with liquid water, so that there is a space for gases above the liquid surface. There is a tight stopper on top of the flask to prevent gases from leaving or entering the system.

Evaporation and condensation are competing processes that occur simultaneously at the liquid water-air interface. The rate of evaporation is defined as the number of water molecules that change phase from liquid to gas each second. The rate of evaporation is mainly set by the temperature of the liquid water. The higher the temperature of the liquid water, the faster the rate of evaporation. At the scale of individual molecules, a molecule of liquid water will evaporate (change phase from liquid to gas) whenever that molecule has enough energy to break free of the chemical bonds it has with neighboring liqiud water molecules. Remember that the temperature measures the average energy possessed by the individual molecules in the substance. In reality, there is a wide range of energies within a substance, with some molecules having more than the average energy and some molecules having less than the average energy. The higher the temperture of the liquid water, the higher the average energy of the liquid molecules, and the more likely that there will be molecules that have enough energy to break free from the liquid bonds. Thus, the higher the temperature, the faster the rate of evaporation. Remember that the process of evaporation is continuously taking place and the rate at which happens is set by the temperature of the closed system.

The rate of condensation is defined as the number of water vapor molecules that change phase from gas to liquid each second. The rate of condensation depends mainly on the vapor pressure in the space above the liquid surface. The vapor pressure increases as the concentration of water vapor in the space above the liquid increases. Thus, the higher the concentration of water vapor molecules above the liquid surface, the faster the rate of condensation. Condensation occurs when a water vapor molecule collides with the liquid water surface, and chemically binds to the liquid water molecules. It should make sense that the higher the vapor pressure, the greater the rate of collisions, and the greater the rate of condensation.

Here is a brief explanation for the previously referenced figure depicting the relationship between vapor pressure and saturation. Panel (a) shows the system immediately after liquid water has been added with no time allowed for evaporation. The pressure gauge shows the pressure of the dry air inside the flask. The initial vapor pressure is zero. Consider the rates of evaporation and condensation. The rate of evaporation is set by the temperature, which is 20°C, while the rate of condensation is zero in panel (a) since the vapor pressure is zero before any time has been allowed for evaporation. Since the rate of evaporation is greater than the rate of condensation, there will be a net movement of liquid water to water vapor. A short time later in panel (b), there is now a measureable vapor pressure. Keep in mind that the rate of evaporation has not changed since the temperature of the system is still 20°C, however the rate of condensation is increasing as the vapor pressure inside the flask increases. This continues until panel (c), when the vapor pressure has now increased to the point where the rate of condensation has now increased to equal the rate of evaporation.

In a closed system, a dynamic equilibrium will be reached, where the rate of evaporation equals the rate of condensation. It is an equilibrum because the number of water vapor molecules above the liquid surface (as measured by the vapor pressure) is no longer changing. It is dynamic because the processes of evaporation and condensation are still happening, but they are happening at equal rates. Throughout panels (a), (b), and (c), the rate of evaporation remains the same because the rate of evaporation is set by the temperature of the system, which remains at 20°C. The rate of condensation though, which started at zero in panel (a), steadily increases as more and more water vapor molecules accumulate above the liquid surface (as measured by the increasing vapor pressure). The rate of condensation eventually increases to match the rate of evaporation in (panel c). At that point the vapor pressure remains the same (equilibrim), and the rates of evaporation and condensation are equal.

When this occurs, the the saturation vapor pressure (e_s ) can be measured, and the air inside the closed system is said to be saturated with water vapor. You may take saturation to mean the capacity or maximum amount of water vapor that will can exist in the air at a particular temperature. This experiment can be repeated at different temperatures to measure the saturation vapor pressure and its dependence on temperature. Graphs relating the saturation vapor pressure to the temperature of the closed system are shown with blue lines below. Try to understand why the saturation vapor pressure (state of dynamic equilibrium) increases as the temperature increaes. At higher temperature, the rate of evaporation is faster. In order to reach dynamic equilibrium, the rate of condensation must equal this faster rate of evaporation. The rate of condensation is set by the vapor pressure. Thus, when the temperature is higher and there is a faster rate of evaporation, there must be a higher vapor pressure so that the rate of condensation is fast enough to equal the rate of evaporation.

This is the point that is being made with panel (d) of the figure. In panel (c), there is a dynamic equilibrium at 20°C where the rate of evaporation equals the rate of condensation and the saturation vapor pressure at 20°C is measured. Now consider heating the system up to 30°C as shown in panel (d). This increase in temperature increases the rate of evaporation so that it is now greater than the rate of condensation. Since the rate of evaporation is greater than the rate of condensation, there are more molecules moving from liquid to gas than from gas to liquid. This causes the vapor pressure inside the flask to increase. As the vapor pressure increases, the rate of condensation increases. This continues until the vapor pressure and rate of condensation increase enough to equal the higher rate of evaporation at 30°C. A new state of dynamic equilibrium will be reached at 30°C. The measured saturation vapor pressure at 30°C is greater than the saturation vapor pressure measured at 20°C, and both the rates of evaporation and condensation at the new dynamic equilibrium are greater at 30°C than they were at 20°C.

It is very important to understand that the higher the air temperature, the higher the saturation vapor pressure, which can be considered as the maximum amount of water vapor that can exist in the air at a given temperature. Often the following statement is made, "warm air can hold more water vapor than cold air." This statement is somewhat misleading in that the other gas molecules in the air to not hold onto water vapor. It just means the maximum capacity for water vapor (known as the saturation vapor pressure) is larger when the air is wsrmer.

It is also very important to realize that the saturation vapor pressure has a strong temperature dependence. As the figures below show, a small increase in temperature, results in a large increase in the saturation vapor pressure or capacity for water vapor in the air. The increase in saturation vapor pressure as temperature increases is exponential, rather than linear. This has strong implications with respect to Earth's climate. Warm, tropical air has a very large capacity for water vapor, which can lead to torrential rains and thunderstorms. Cold, polar air has a very low capacity for water vapor, which limits the amount of snow that can fall.

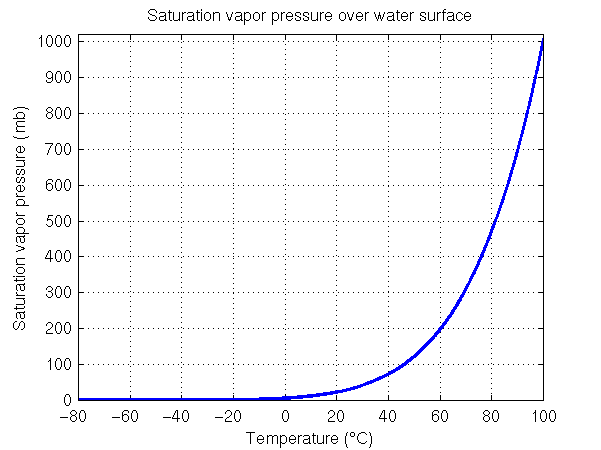
The figure on the left shows the saturation vapor pressure for water for the range of temperatures typical at the surface of the Earth. Note from the figure caption that a temperature increase from 10°C to 30°C (50°F to 86°F), which can happen over the course of a day, causes the saturation vapor pressure to increase by a factor of three and a half, from 12 mb to 42 mb. Thus a small change in temperature results in a large change in the saturation vapor pressure or the maximum amount of water vapor that can exist in the air. It is important to understand that saturation vapor pressure (or the maximum amount of water vapor that can be in the air) increases exponentially as temperature increases.

The sharp increase in saturation vapor pressure with increasing temperature continues beyond 40°C (104°F). Water will boil when the saturation vapor pressure is equal to the surrounding air pressure. At sea level, water will boil when the saturation vapor pressure equals the sea level pressure, which has an average value of 1013 mb. As many of you know this happens when the water temperature is 100°C or 212°F. This is shown in the figure on the right side, which extends the temperature range up to 100°C. When water boils, bubbles of water vapor (gas form of water) are able form under the surface of the water and rise upward. The gas pressure inside these water vapor bubbles must be able to hold up against the surrounding pressure or they will be crushed. If the saturation vapor pressure is less than the surrounding air pressure, any bubble of water vapor that tries to form will be crushed by the surrounding air pressure. Therefore depending upon the exact value of the surrounding air pressure, water will begin to boil at a specific temperature, i.e., the temperature where the saturation vapor pressure is equal to the surrouding air pressure.

Finally, note that the saturation vapor pressure sets a limit on the maximum possible water vapor that can be in the air at a given air temperature. The actual amount of water vapor in the air (measured by the vapor pressure) is often less than the saturation amount. A closed system experiment like the one described above will always come to a state of saturation. However, when not in a closed system, the vapor pressure in a sample of air can range anywhere from zero water vapor to as high as the saturation vapor pressure, but never higher. The concept of relative humidity will be discussed on the next page. The relative humidity is the measured vapor pressure divided by the saturation vapor pressure. The relative humidity is 100% when the vapor pressure equals the saturation vapor pressure, though it can be any value from 0% to 100%, but never higher than 100%, since there can never be more water vapor than the capacity or saturation amount, which is set by the air temperature and its relation to saturation vapor pressure. Looking at the graphs of saturation vapor pressure above, this means that the vapor pressure (water vapor content) of a sample of air can is allowed to be anywhere from on the blue line (the saturation vapor pressure) to locations on the graph that are below and to the right of the blue line (saturation), but never above the blue (saturation) line.

Evaporation and condensation in the atmosphere

Near the Earth's surface, the vapor pressure is usually less than the saturation vapor pressure. (NOTE: the actual vapor pressure of the air can vary from zero up to the saturation vapor pressure). Therefore, the rate of evaporation is greater than the rate of condensation, i.e., liquid water near the Earth's surface is continually evaporating (changing phase from liquid to gas). You can easily convince yourself that this is true by leaving out a glass of water. All of the liquid will eventually evaporate. The reason the air near the ground does not reach saturation is because after the water evaporates, the water vapor is able to move away from the surface. It is not trapped as in the closed experiment described above.

Once water has evaporated it becomes part of the gases that make up the atmosphere. When air rises upward, it cools (the reason rising air cools will be explained later). As air cools, its saturation vapor pressure decreases, in other words, the maximum amount of water vapor that the air can hold decreases. If the air rises high enough and cools sufficiently, it will not be able to hold all the water vapor it contains. When this happens, water vapor must condense back to liquid water. This is how clouds form. Clouds are composed of tiny droplets of liquid water (and possibly ice). Water vapor is an invisible gas and cannot ever be seen. If you see it, e.g., clouds, steam, your breath on a cold day, it must be liquid water droplets. We will talk more about clouds soon.

An Analogy to Help Understand the Concept of Water Vapor Saturation

Let's try an analogy that might help you to better understand the concept of saturation with respect to water vapor. Consider a movie theater with seats. The number of seats in the theater represents the saturation vapor pressure. The size of the movie theater can change ... a small movie theater has few seats, while a large movie theater has many seats. The size of the theater and number of seats gets larger as the air temperature goes up (increases) and the size of the theater gets smaller as the air temperature goes down (decreases). The seating capacity, which represents the saturation amount, is determined by the air temperature.

Further consider the number of people sitting in seats as the vapor pressure (water vapor molecules). There can be anywhere from zero people in the seats (vapor pressure = 0) up to every available seat being occupied with people (vapor pressure = saturation vapor pressure). The size of the theater represented by the number of available seats is the capacity or saturation amount of water vapor.

A closed system, like the flask with liquid water in bottom and a stopper on top, can be represented by a long line of people waiting to get into the theater. People entering the theater represent evaporation or the phase change from liquid water to water vapor (gas). People leaving the theater and getting back in line represent condensation or the phase change from water vapor (gas) to liquid water. A closed system will quickly reach saturation or a state where every seat is filled. It is a dynamic equilibrium, which by analogy means that there are always people leaving the theater (condensing from water vapor to liquid water) at the same rate the new people are entering (evaporating from liquid water to water vapor).

As an analogy to panel (d) of the closed system figure referenced above, consider the theater in saturation at a temperature of 20°C. The temperature sets the size of the theater and the number of available seats. If the temperature is increased to 30°C, the theater expands and more seats are available. It also increases the rate of evaporation and people enter the theater more quickly (they have more energy when it is warmer). In a very short time, the theater fills up again to saturation, but it is larger with more seats at the higher temperature. Once it reaches this new higher filled capacity (or saturation amount), every time a new person enters from the line (evaporation) another is forced to leave their seat to get back in line (condensation) and there is a new state of dynamic equilibrium.

Now consider the opposite. We start with a theater filled to capacity (saturated), but this time reduce or lower the temperature. This reduces the size of the theater and number of seats available, so people are forced to leave the theater (condense) until the number of people left in the theater reduces to the lower capacity (saturation amount) or number of seats now available.

On the next reading page, we consider the concept of relative humidity, which is a fraction equal to the equal to the number of seats occupied (vapor pressure) divided by the total number of seats available (saturation vapor pressure or capacity). The relative humidity can be anywhere between 0% of capacity and 100% of capacity, but never higher than 100%. If there is ever a situation where there are more people in the theater than seats available, then the number of people above capacity must leave the theater. This represents condensation or conversion of water vapor (people in the theater) to liquid water (people forced out of the theater and back into line). This is actually a good analogy for what happens when dew forms or water vapor is forced to condense onto the outside of a cold object. The object must cool down to the point where there is more water vapor molecules in the air than the saturation amount for the temperature of the object. By analogy consider a theater that is not filled to capacity, for example, suppose it is half full. The relative humidity of the theater is 50%. If the air temperature falls, then the size of the theater and the number of available seats (capacity) is reduced, so for the same number of people in the theater, the relative humidity in now greater than 50%. Continue to lower the temperature and the number of seats available and eventually the number of people inside will equal the capacity of the theater, which makes the relative humidity 100%. The temperature at which the size of theater shrinks so that the number of seats is exactly equal to the number of people inside is known as the dew point temperature, i.e., the temperature to which air must be cooled for it to become saturated with water vapor. Again by analogy, the dew point temperature is the temperature that shrinks the size of the theater to the point where every seat is taken by the number of people inside. If the theater is further cooled to a temperature lower than the dew point temperature, then people are forced to leave (condensation or the formation of dew) since there would be fewer seats available than the number of people that were originally in the theater.

Hopefully, this analogy was helpful to some of you. The concepts of relative humidity and dew point temperature are covered in the next reading page.