Wednesday Jan. 30, 2008

The Practice Quiz is one week from today.  A Practice Quiz Study Guide is now available online.  Study guides should also appear about one week before future quizzes this semester.  Click here is you would like to download the study guide in Microsoft WORD format for printing.  You will find sample questions listed on the Study Guide taken from Fall 2000 NATS 101 quizzes.  Click here to select and download copies of those quizzes.

The following announcement was made at the beginning of class:
At least one student in  class is in need of a note-taker.  If you feel you take clear, concise notes and are willing to share a copy with a student with a disability, please come to the front of the classroom at the end of class so that you can meet the student.  You will be provided with arbonless copy paper to take notes and will be formally recognized through a letter of volunteeer service for your portfolio or resume.

We are ready to move back into the middle part of Chapter 1.  We will be looking at how atmospheric characteristics such as air temperature, air pressure, and air density change with altitude.  In the case of air pressure we first need to understand what pressure is and what can cause it to change.

An iron bar was passed around at the beginning of class.  You were supposed to guess how much it weighed.

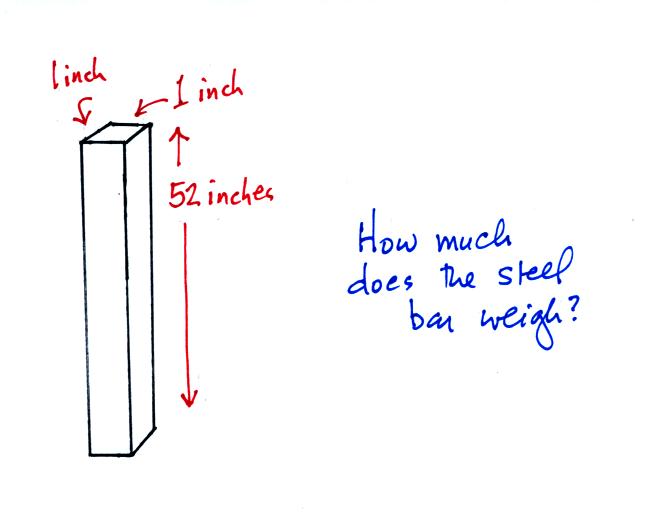
We come back to the iron bar later in the class.

What follows is a little more detailed discussion of the basic concepts of mass, weight, and density than is found on p. 23 in the photocopied Classnotes.

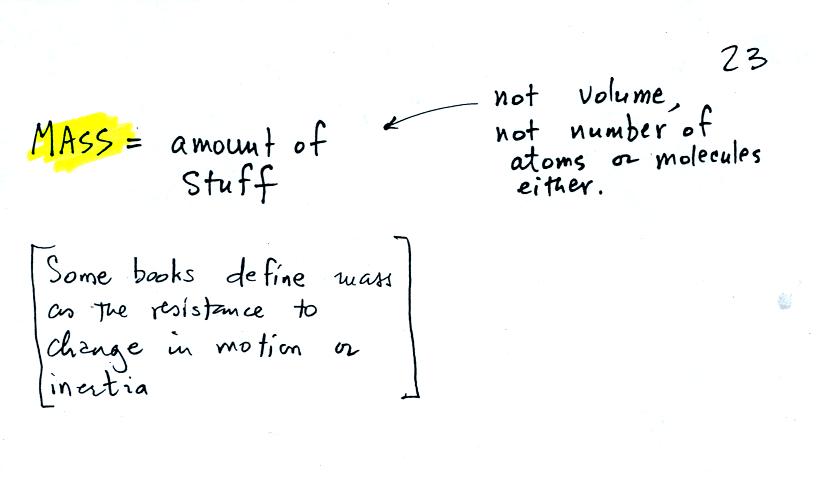
Before we can learn about atmospheric pressure, we need to review the terms mass and weight.  In some textbooks you'll find mass defined at the "amount of stuff."  Other books will define mass as inertia or as resistance to change in motion.  The next picture illustrates both these definitions.  A Cadillac and a volkswagen have both stalled in an intersection.  Both cars are made of steel.  The Cadillac is larger and has more steel, more stuff, more mass.  The Cadillac is also much harder
 to get moving than the VW, it has a larger inertia (it would also be harder to slow down if it were already moving).

It is possible to have two objects with the same volume but very different masses.  The bottles of water and mercury that were passed around class on Monday were an example (thanks for being careful with the mercury).

To understand why there is such a difference in mass and weight you need to look at the water molecules and mercury atoms on an atomic scale.



Mercury atoms are built up of many more protons and neutrons than a water molecule (also more electrons but they don't have nearly as much mass as protons and neutrons).  The mercury atoms have 11.1 times as much mass as the water molecule.  This doesn't quite account for the 13.6 difference in density.  Despite the fact that they contain more protons and neutrons, the mercury atoms must also be packed closer together than the molecules in water.




Weight is a force and depends on both the mass of an object and the strength of gravity. 

We tend to use weight and mass interchangeably because we spend all our lives on earth where gravity never changes.




Any three objects that all have the same mass would necessarily have the same weight. Conversely


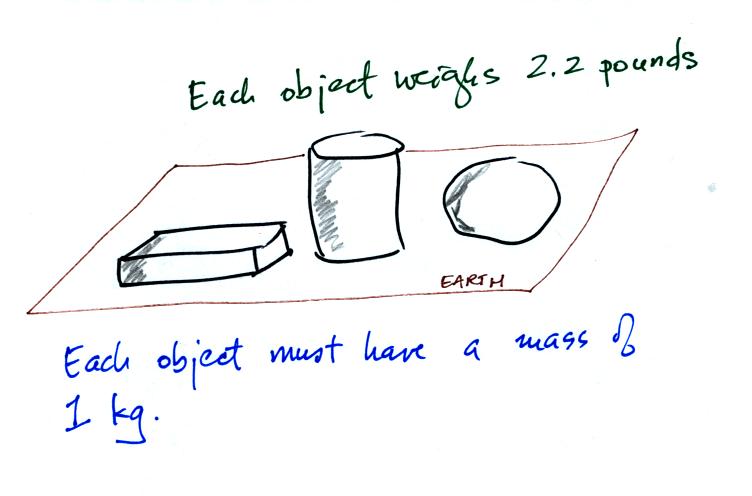
Three objects with the same weight would also have the same mass.

The difference between mass and weight is clearer (perhaps) if you compare the situation on the earth and on the moon.

If you carry an object from the earth to the moon, the mass remains the same (its the same object, the same amount of stuff) but the weight changes because gravity on the moon is weaker than on the earth.



Definition and illustrations of high and low density.


The air that surrounds the earth has mass.  Gravity pulls downward on the atmosphere giving it weight.  Galileo conducted (in the 1600s) a simple experiment to prove that air has weight. 

Pressure is defined as force divided by area.  Air pressure is the weight of the atmosphere overhead divided by area the air is resting on.  Atmospheric pressure is determined by and tells you something about the weight of the air overhead.

Under normal conditions a 1 inch by 1 inch column of air stretching from sea level to the top of the atmosphere will weigh 14.7 pounds.  Normal atmospheric pressure at sea level is 14.7 pounds per square inch (psi, the units you use when you fill up your car or bike tires with air).



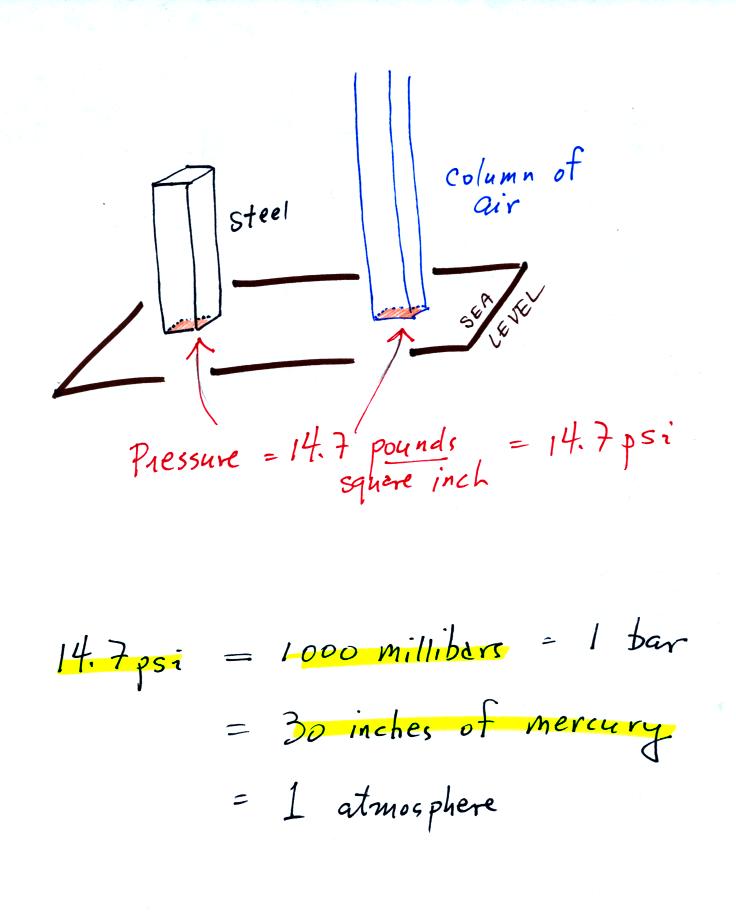
The iron bar also weighs 14.7 pounds.  When it is standing on end the bar exerts a pressure of 14.7 pounds per square inch on the ground, the same as a 1 inch by 1 inch column of air at sea level altitude.

Some of the other commonly used pressure units are shown above.  Typical sea level pressure is 14.7 psi or about 1000 millibars (the units used by meterologists) or about 30 inches of mercury (refers to the reading on a mercury barometer).  If you ever find yourself in France needing to fill your automobile tires with air, remember that the air compressor scale is probably calibrated in bars.  2 bars of pressure would be equivalent to 30 psi.

The word "bar" has a lot of meanings:


An iron bar was passed around in class.  A lot of people will be watching the Super
Bowl this weekend in a bar.  The word bar also refers to pressure.
Pressure at sea level is determined by the weight of the air overhead.  What about pressure at some level above sea level?
We can use the stack of bricks sketched below to try to answer this question.

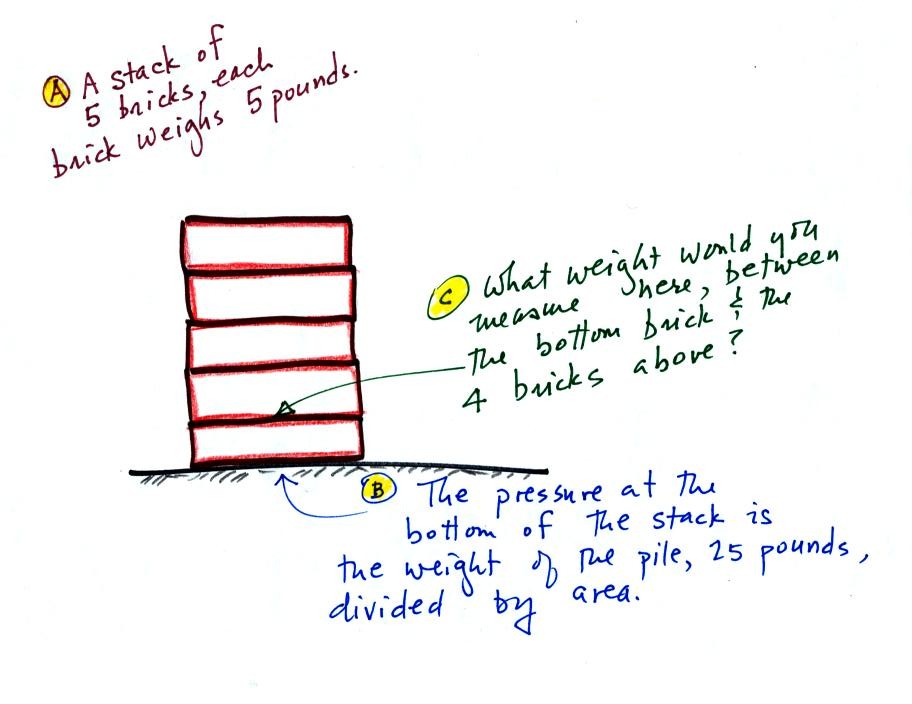
At the bottom of the pile you would measure a weight of 25 pounds (5 bricks x 5 pounds per brick).  If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks still above.  In the atmosphere pressure at any level is determined by the weight of the air still overhead.  Pressure decreases with increasing altitude because there is less and less air remaining overhead.
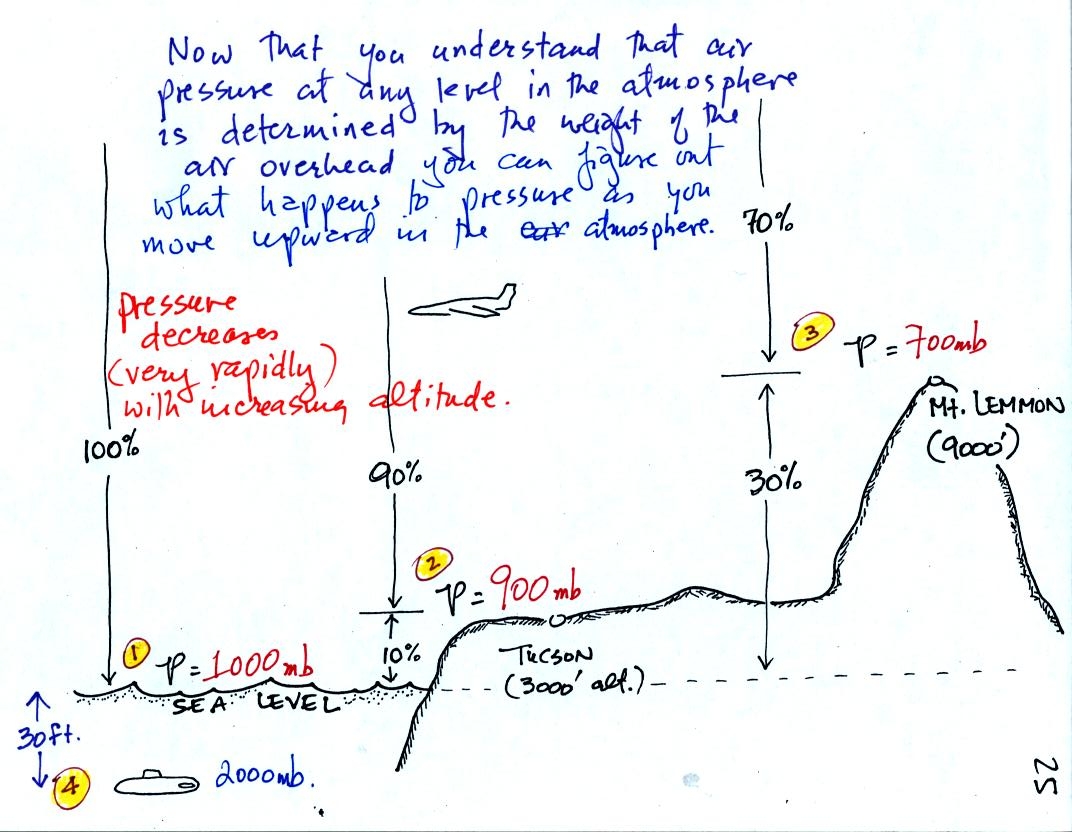At sea level altitude, at Point 1, the pressure is normally about 1000 mb.  That is determined by the weight of all of the air in the atmosphere. 

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of the valley is lower than that).  At 3000 ft. 10% of the air is below, 90% is still overhead.  It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson.  If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb. 

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3).

Pressure decreases rapidly with increasing altitude.

Point 4 shows a submarine at a depth of about 30 ft.  The pressure there is determined by the weight of the air and the weight of the water overhead.  Water is much denser and much heavier than air.  At 30 ft., the pressure is already twice what it would be at the surface of the ocean.
Now we'll take this a step further and learn that the rate of pressure decrease with increasing altitude depends on the air density.


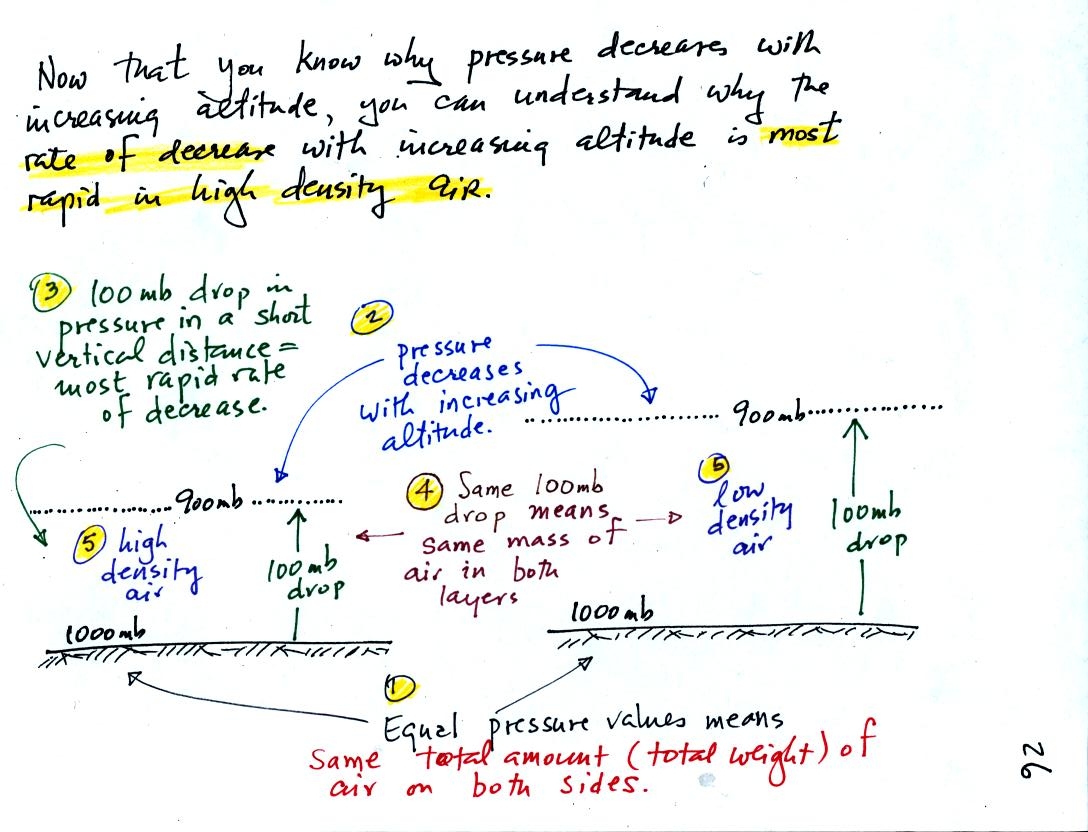
1000 mb at Point 1 is a reasonable value for sea level pressure.  The fact that the pressures are equal at the bottoms of both sides of the picture means that the weight of the atmosphere at the bottom of the picture on the left is the same as the weight of the atmosphere at the bottom of the picture at right.  The only way this can be true is if there is the same total amount (mass) of air in both cases.

Point 2 - Moving upward from the ground we find that pressure decreases to 900 mb at the level of the dotted line in the picture at left.  This is what you expect, pressure decreases with increasing altitude. 

Point 3 - The most rapid rate of pressure decrease with increasing altitude is occurring in the picture at left.

Point 4 - Since there is a 100 mb drop in both the layer at left and in the layer at right, both layers must contain the same amount (mass) of air.

Point 5 - The air in the picture at left is squeezed into a thinner layer than in the picture at right.  The air density in the left layer is higher than in the layer at right.

We used and analyzed this picture to prove to ourselves that the rate of pressure decrease with altitude is higher in dense air than in lower density air.

This is a fairly subtle but important concept.  We will use this concept several times during the semester.  In particular we will need this concept to understand why hurricanes can intensify as they do.