Thu., Jan. 31 notes

Thursday Jan. 31, 2008

The Practice Quiz is one week from today. A Practice Quiz Study Guide is now available online. Study guides should also appear about one week before future quizzes this semester. Click here is you would like to download the study guide in Microsoft WORD format for printing. You will find sample questions listed on the Study Guide taken from Fall 2000 NATS 101 quizzes. Click here to select and download copies of those quizzes.

The iron bar also weighs 14.7 pounds. When it is standing on end the bar exerts a pressure of 14.7 pounds per square inch on the ground, the same as a 1 inch by 1 inch column of air at sea level altitude.

Some of the other commonly used pressure units are shown above. Typical sea level pressure is 14.7 psi or about 1000 millibars (the units used by meterologists) or about 30 inches of mercury (refers to the reading on a mercury barometer).

If you ever find yourself in France needing to fill your automobile tires with air, remember that the air compressor scale is probably calibrated in bars. 2 bars of pressure would be equivalent to 30 psi.

The word "bar" has a lot of meanings:

An iron bar was passed around in class. A lot of people will be watching the Super
Bowl this weekend in a bar. The word bar also refers to pressure.

Pressure at sea level is determined by the weight of the air overhead. What about pressure at some level above sea level?
We can use the stack of bricks sketched below to try to answer this question.

At the bottom of the pile you would measure a weight of 25 pounds (5 bricks x 5 pounds per brick). If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks still above. In the atmosphere pressure at any level is determined by the weight of the air still overhead. Pressure decreases with increasing altitude because there is less and less air remaining overhead.

At sea level altitude, at Point 1, the pressure is normally about 1000 mb. That is determined by the weight of all of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of the valley is lower than that). At 3000 ft. 10% of the air is below, 90% is still overhead. It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson. If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb.

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3).

Pressure decreases rapidly with increasing altitude.

Point 4 shows a submarine at a depth of about 30 ft. The pressure there is determined by the weight of the air and the weight of the water overhead. Water is much denser and much heavier than air. At 30 ft., the pressure is already twice what it would be at the surface of the ocean.

Now we'll take this a step further and learn that the rate of pressure decrease with increasing altitude depends on the air density.

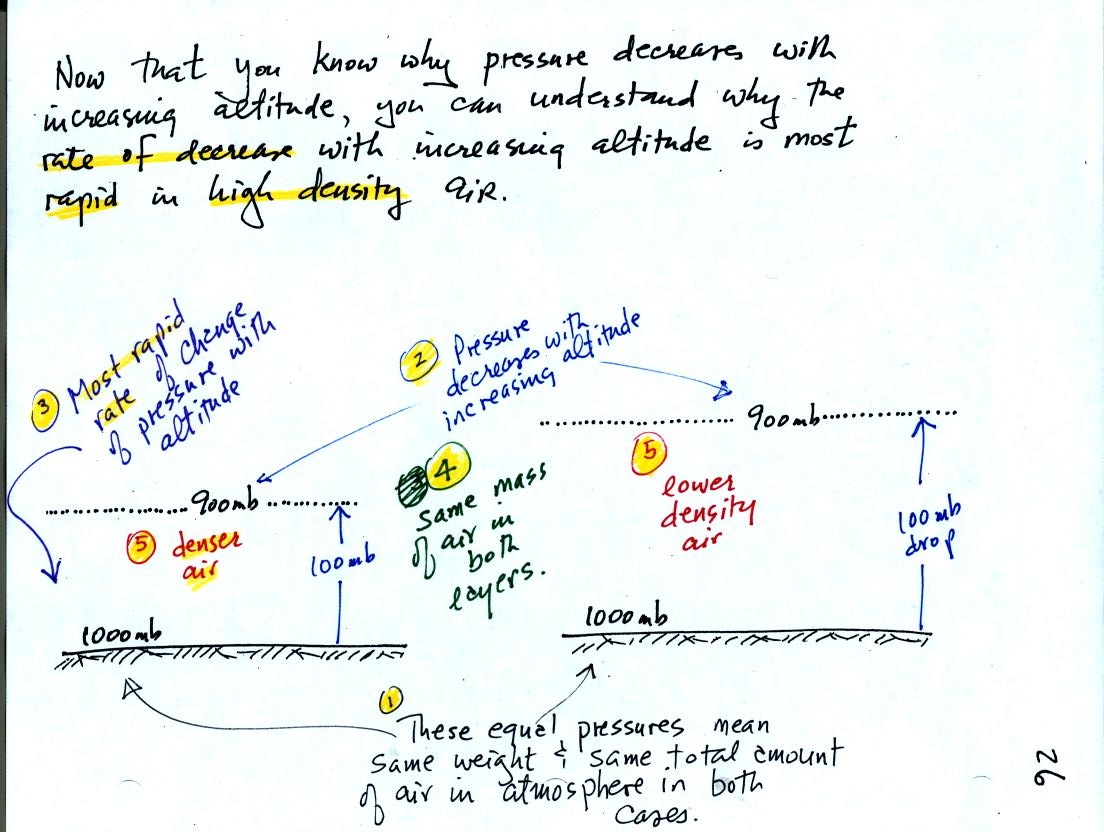
1000 mb at Point 1 is a reasonable value for sea level pressure. The fact that the pressures are equal at the bottoms of both sides of the picture means that the weight of the atmosphere at the bottom of the picture on the left is the same as the weight of the atmosphere at the bottom of the picture at right. The only way this can be true is if there is the same total amount (mass) of air in both cases.

Point 2 - Moving upward from the ground we find that pressure decreases to 900 mb at the level of the dotted line in the picture at left. This is what you expect, pressure decreases with increasing altitude.

Point 3 - The most rapid rate of pressure decrease with increasing altitude is occurring in the picture at left.

Point 4 - Since there is a 100 mb drop in both the layer at left and in the layer at right, both layers must contain the same amount (mass) of air.

Point 5 - The air in the picture at left is squeezed into a thinner layer than in the picture at right. The air density in the left layer is higher than in the layer at right.

We used and analyzed this picture to prove to ourselves that the rate of pressure decrease with altitude is higher in dense air than in lower density air.

This is a fairly subtle but important concept. We will use this concept several times during the semester. In particular we will need this concept to understand why hurricanes can intensify as they do.

We really didn't work through the following figures at all (except for filling in the box at the bottom of p. 28 with the English and Metric units for mass and weight). With a little thought you will understand the terms that appear in Newton's Law of Universal Gravitation and why they appear in either the numerator (direct proportionality) or in the denominator (inverse proportionality).

The gravitational attraction between two objects (M and m in the figures) depends first of all on the distance separating the objects. The gravitational force becomes weaker the further away the two objects are from each other. In the bottom picture above and the top figure below we see that the attractive force also depends on the masses of the two objects.

The complete formula is shown in the middle of the page above. G is a constant. On the surface of the earth G, M, and R don't change. The gravitational acceleration, g, is just G times M_earth divided by ( R_earth )² . To determine the weight (on the earth's surface) of an object with mass m you simply multiply m x g.

Down at the bottom of the page are the Metric and English units of mass and weight. You have probably heard of pounds, grams, and kilograms. You might not have heard of dynes, Newtons, and slugs.

Here's another page from the photocopied Class Notes that we didn't cover in class. The weight of a person on the earth and the moon is calculated in English and metric units.

The mass of a person would be the same on the earth and on the moon. The weight of a person depends on the person's mass and on the strength of gravity (the acceleration of gravity term, the g variable below).

(1) The course instructor weighs about 160 pounds. In (2) we see that the gravitational acceleration is 32 ft/sec2 in English units. The meaning of this value is shown in (3). Gravity will cause a falling object to fall 32 ft/sec faster with every second it continues to fall. Dividing the instructor's weight by the gravitation acceleration in (4) we obtain the instructor's mass, 5 slugs, in English units.

In metric units, the instructor has a mass of 73 kilograms (5). The gravitation acceleration is 9.8 m/sec (6). Multiplying these two values, in (7), we find that the instructor weighs 715 Newtons.

On the moon, the mass stays the same. Gravity is weaker, so the value of g is smaller. The instructor would weigh quite a bit less (117 Newtons or 26 pounds) on the moon compared to the earth.

Here's another topic that we'll beat into submission, trying to understand how a mercury barometer works (it's used to measure atmospheric pressure). You'll find most of what follows on p. 29 in the photocopied Class Notes.

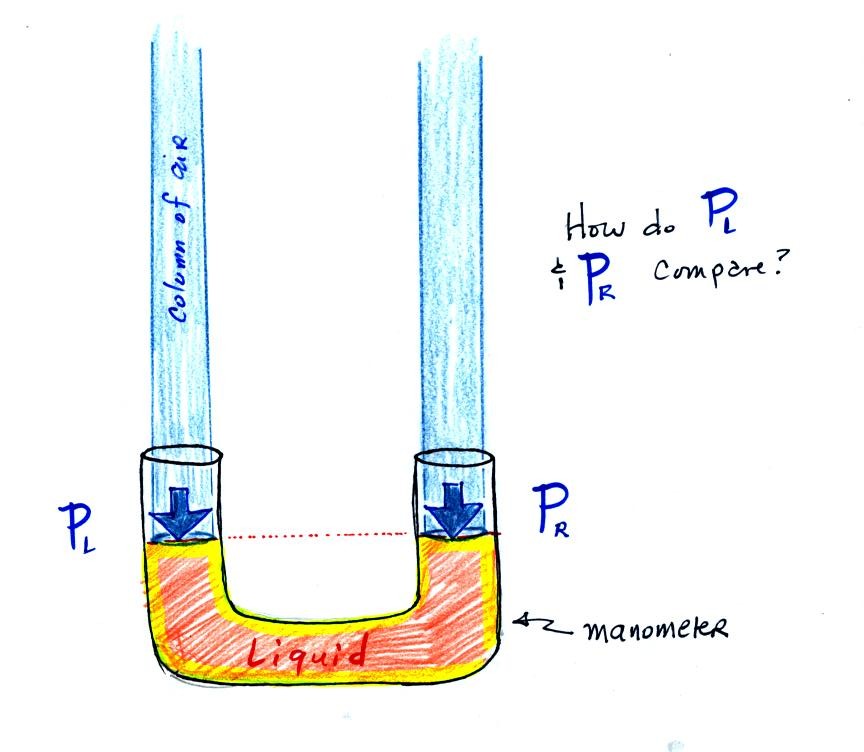
The instrument above ( a u-shaped glass tube filled with a liquid of some kind) is a manometer and can be used to measure pressure difference. The two ends of the tube are open so that air can get inside and air pressure can press on the liquid. Given that the liquid levels on the two sides of the manometer are equal, what could you about P_L and P_R?

The liquid can slosh back and forth just like the pans on a balance can move up and down. A manometer really behaves just like a pan balance.

P_L and P_R are equal (note you don't really know what either pressure is just that they are equal).

Now the situation is a little different, the liquid levels are no longer equal. You probably realize that the air pressure on the left, P_L, is a little higher than the air pressure on the right, P_R. P_L is now being balanced by P_R + P acting together. P is the pressure produced by the extra fluid on the right hand side of the manometer (the fluid that lies above the dotted line). The height of the column of extra liquid provides a measure of the difference between P_L and P_R.

Next we will go an extreme and close off the right hand side of the manometer.

Air pressure can't get into the right tube any more. Now at the level of the dotted line the balance is between P_air and P (pressure by the extra liquid on the right). If P_air changes, the height of the right column, h, will change. You now have a barometer, an instrument that can measure and monitor the atmospheric pressure.

Barometers like this are usually filled with mercury. Mercury is a liquid. You need a liquid that can slosh back and forth in response to changes in air pressure. Mercury is also dense which means the barometer won't need to be as tall as if you used something like water. A water barometer would need to be over 30 feet tall. With mercury you will need only a 30 inch tall column to balance the weight of the atmosphere at sea level under normal conditions (remember the 30 inches of mercury pressure units mentioned earlier). Mercury also has a low rate of evaporation so you don't have much mercury gas at the top of the right tube.

Finally here is a more conventional barometer design. The bowl of mercury is usually covered in such a way that it can sense changes in pressure but not evaporate and fill the room with poisonous mercury vapor.

The figure above (p. 30 in the photocopied Class Notes) first shows average sea level pressure values (1000 mb or 30 inches of mercury are close enough in this class).

Sea level pressures usually fall between 950 mb and 1050 mb.

Record high sea level pressure values occur during cold weather.

Record low pressure values have all been set by intense hurricanes (the record setting low pressure is the reason these storms were so intense). Hurricane Wilma in 2005 set a new record low sea level pressure reading for the Atlantic. Hurricane Katrina had a pressure of 902 mb. You'll find a list of the most intense, destructive, and deadly hurricanes on p. 146a.

Air pressure is a force that pushes downward, upward, and sideways. If you fill a balloon with air and then push downward on it, you can feel the air in the balloon pushing back (pushing upward). You'd see the air in the balloon pushing sideways as well.

The bottom person in the people pyramid above must push upward with enough force to support the other people. The air in a layer at the bottom of the atmosphere must do the same thing. It pushes upward with enough force to support the weight of all the air overhead.

The air pressure in the four tires on your automobile push down on the road (that's something you would feel if the car ran over your foot) and push upward with enough force to keep the 1000 or 2000 pound vehicle off the road.

We finished class with a demonstration of the upward force caused by air pressure.
The demonstration is summarized on p. 35a in the photocopied Classnotes.

We'll come back to this demonstration briefly in class next Tuesday and look at the actual forces being exerted on the water and the glass
First the case of a water balloon.

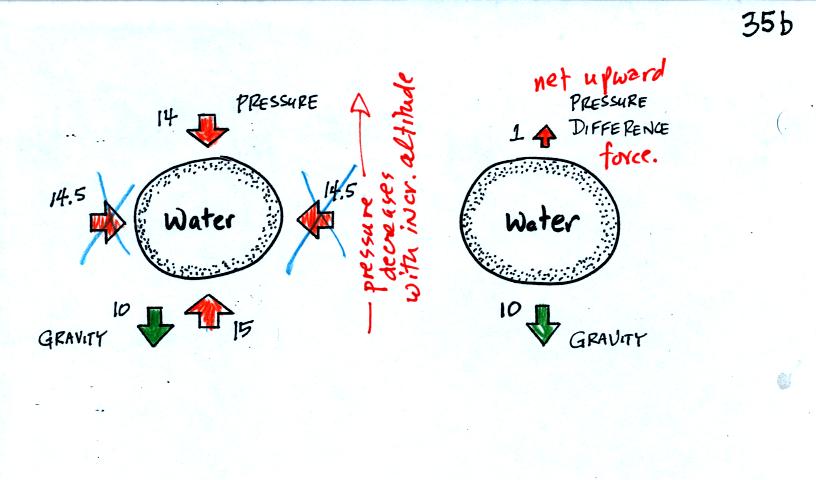
The figure at left shows air pressure (red arrows) pushing on all the sides of the balloon. Because pressure decreases with increasing altitude, the pressure pushing downward on the top of the balloon is a little weaker (strength=14) than the pressure pushing upward at the bottom of the balloon (strength=15). The two sideways forces cancel each other out. The total effect of the pressure is a weak upward force (shown on the right figure, you might have heard this called a bouyant force). Gravity exerts a downward force on the water balloon. In the figure at right you can see that the gravity force (strength=10) is stronger than the upward pressure difference force (strength=1). The balloon falls as a result.

In the demonstration a wine glass is filled with water. A small plastic lid is used to cover the wine glass. You can then turn the glass upside down without the water falling out.

All the same forces are shown again in the left most figure. In the right two figures we separate this into two parts. First the water inside the glass isn't feeling the downward and sideways pressure forces (because they're pushing on the glass). Gravity still pulls downward on the water but the upward pressure force is able to overcome the downward pull of gravity. The upward pointing pressure force is used to overcome gravity not to cancel out the downward pointing pressure force.

The demonstration was repeated using a 4 Liter flash (more than a gallon of water, more than 8 pounds of water). The upward pressure force was still able to keep the water in the flask (much of the weight of the water is pushing against the sides of the flask which the instructor was supporting with his arms).