Thursday Feb. 12, 2009
We'll finish up the material on small ions today.
On Tuesday we looked at some of the sources of radiation that ionize
air. When neutral oxygen or nitrogen are ionized you are left
with
a positively charged N2 or O2 molecule and a free
electron. The
electron subsequently attaches to neutral oxygen molecules (but not to
nitrogen).
We can estimate how long it will be before the electron attaches
to a neutral molecule. In the case of attachment to oxygen we
need to know the oxygen concentration in air, [O2], and a rate
constant k1.
We can use the ideal gas law equation to determine the oxygen
concentration. Electron attachment occurs very quickly, in a few
or a few tens of nanoseconds.
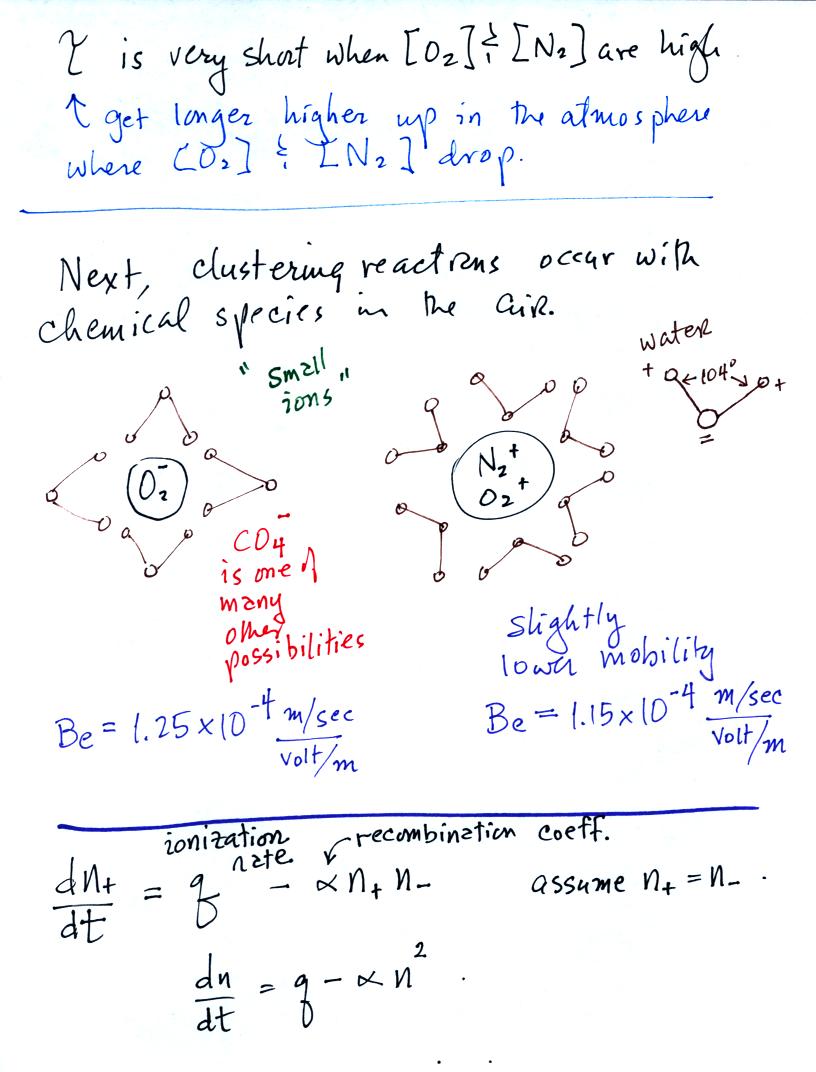
The next step in small ion formation is clustering of a chemical
species of some kind around the positively and negatively charged
ions. This occurs on a millisecond time scale. In the
figure above we show ionized nitrogen and oxygen molecules. This
is just one possibility. CO4-
is apparently one of the more common ions found in the centers of these
molecular clusters
also. And something other than water may envelope the central ion.
The mobilities of positively and negatively charged small ions are
slightly different. Typical values are shown above. The
positively charged small ions have a slightly higher mobility (slightly
lower drift speed) than the negatively charged ions.
That's an ion balance equation at the bottom of the page above.
At this point the small ion concentration will depend on the ion
production rate, q, and the rate at which ions recombine and neutralize
each other. The next figure gives the general and steady state
solutions to the ion balance equation.
The small ion concentration reaches steady state pretty quickly.
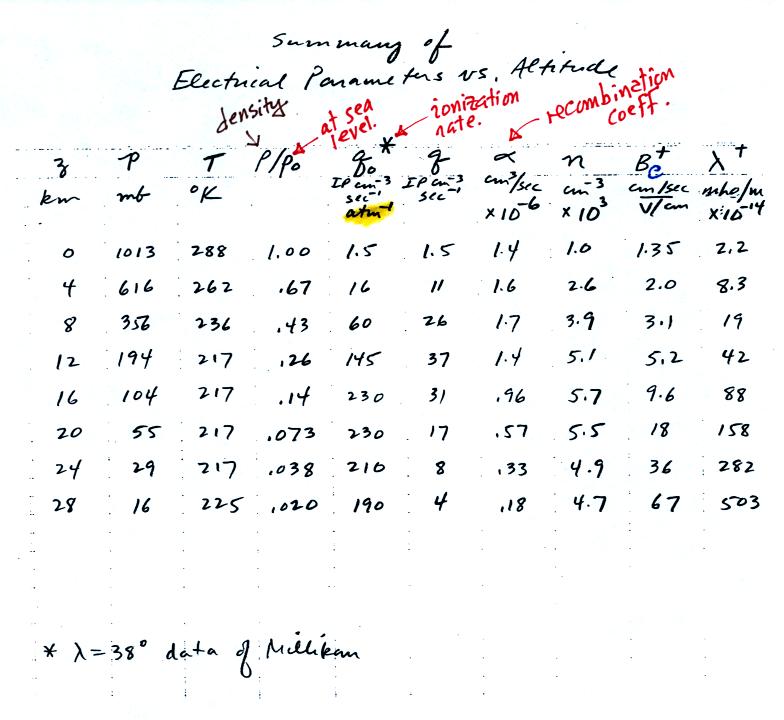
Here is a
table of typical electrical parameter values at different altitudes.
This information was compiled by Dr. Krider and was on a handout
distributed in class.
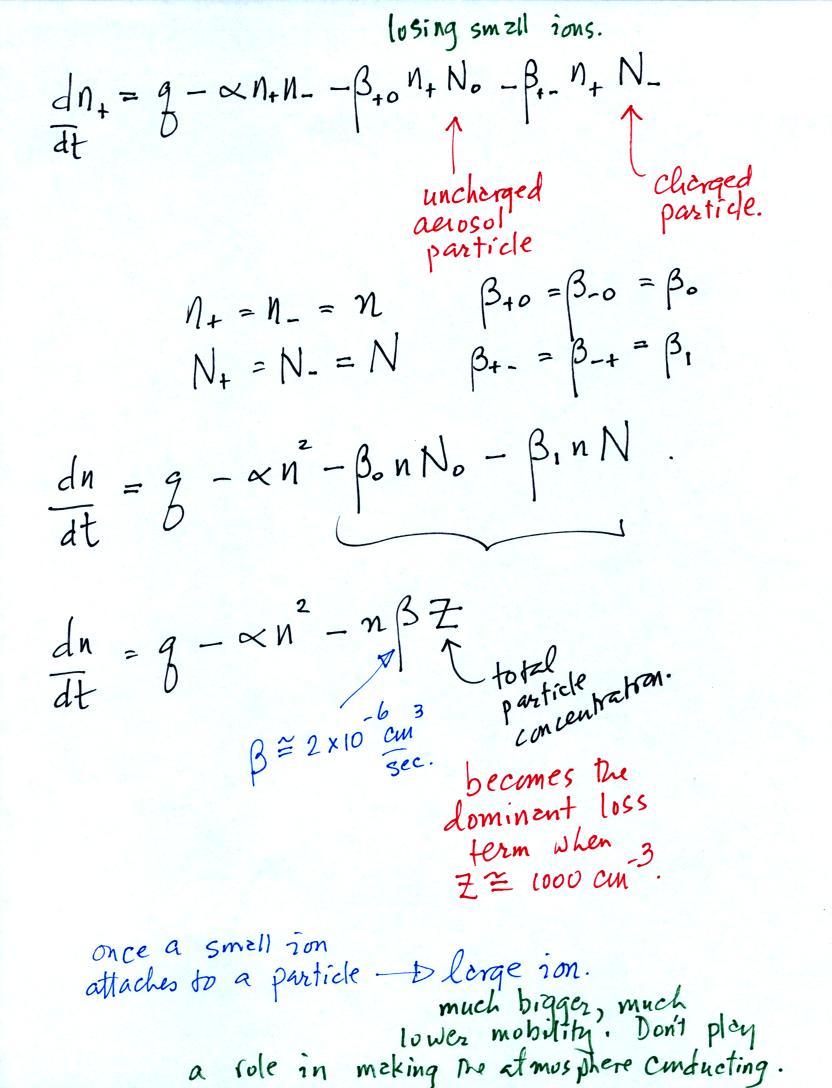
The small ion balance equation has been modified by adding two
loss
terms. The first involves small ion attachment to a neutral
aerosol particle. The second is small ion attachment to a charged
aerosol particle of the opposite polarity.
The first balance equation is often simplified somewhat by lumping
together the charged and uncharged aerosol particles. Z above is
the total aerosol concentration.
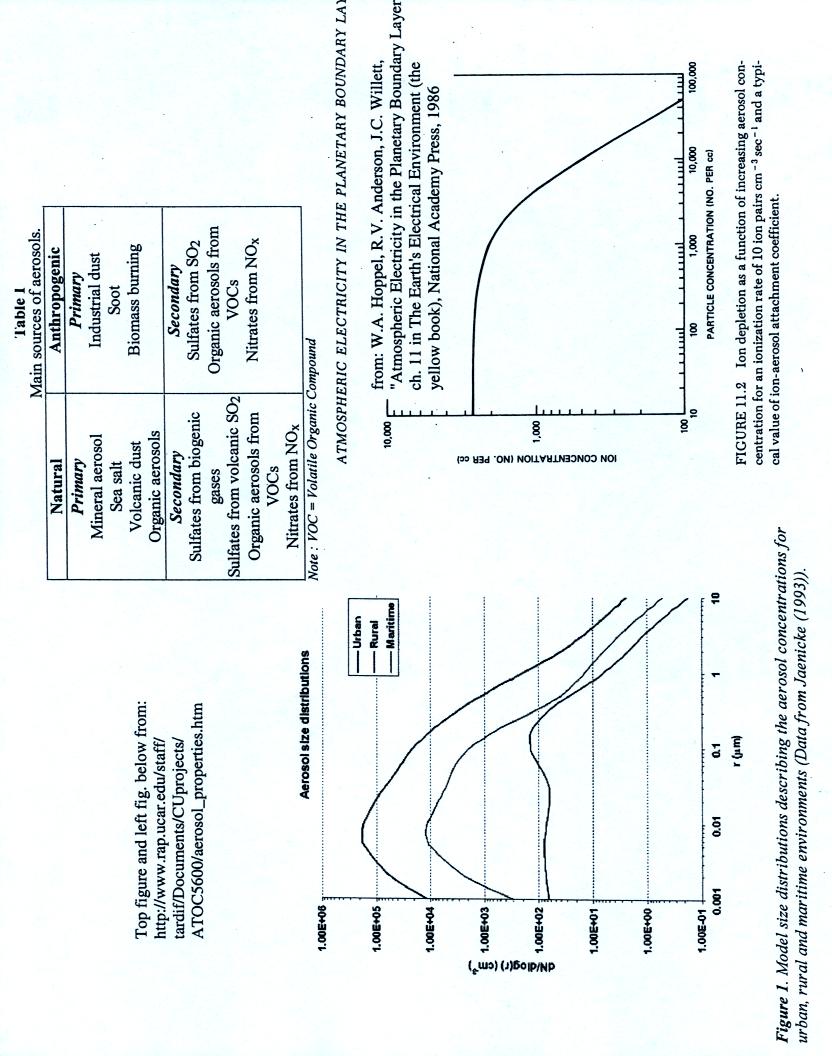
This next page is a copy of a handout with some properties of aerosols.
The
remaining notes were on a handout distributed in class. We didn't
really go through this material in detail, this is more "for your
information" kind of stuff.
On the page above and the one below, a pretty good estimate of the
attachment coefficient to neutral aerosol particles can be estimated
using molecular diffusion.

The attachment to charged aerosol
particles can also be estimated to within a factor of two using a
relatively simple approach.
Small ion
recombination is usually much smaller than loss by attachment to
aerosol particles. Here is the steady state solution when
recombination is neglected.
On this
next page we look at what fraction of the aerosol particles (total
concentration = Z) are uncharged. The calculated estimate is
compared with measurements. The agreement is not very good,
especially for smaller particles.
On the next page, the uncharged fraction is computed using
Boltzmann theory.
A couple of points to note: the uncharged fraction approaches 1 for the
smaller particles. The smaller particles that are charged only
hold one electronic charge.