Thursday Jan. 22, 2009
We'll spend at least a couple of weeks reviewing some basic laws from
electrostatics. Examples from atmospheric electricity that make
use of some of these principles will be inserted along the way.
We'll start with Coulomb's Law. Many of the figures below were
redrawn after class for improved clarity.
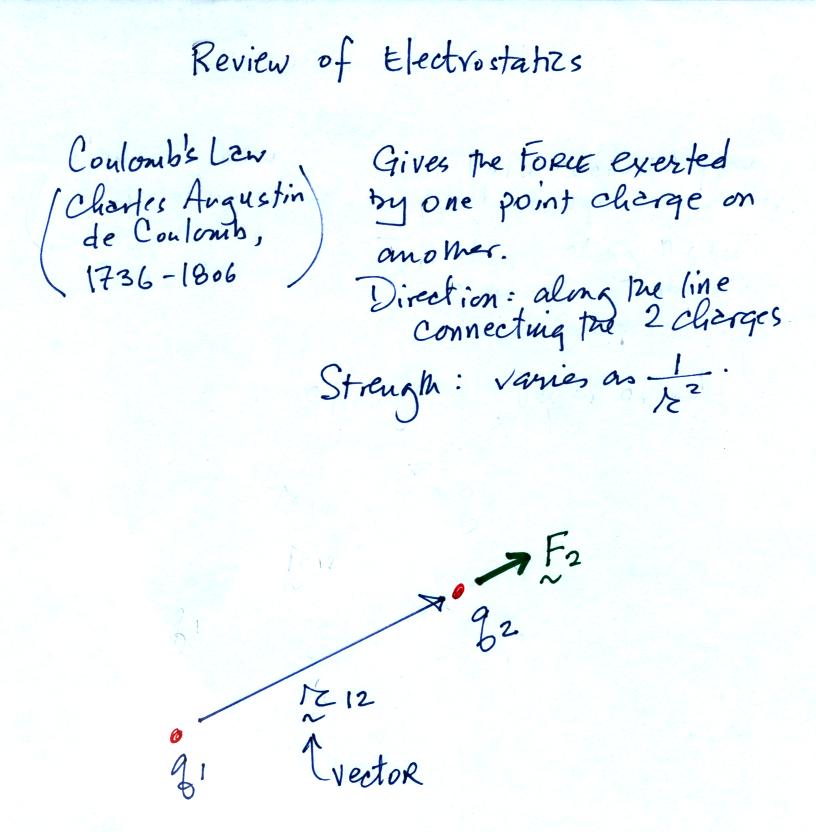
The force that q1exerts on q2 is given below and depends on the
product of q1 and q2 and varies as 1/(distance)2

The principle of superposition
applies: when multiple charges are present, the force exerted on one of
the charges is the vector sum of the forces exerted on the charge by
all the other charges. Note the vector and unit vector notation
being used above. We will mostly be using the MKS system of units
in this class.
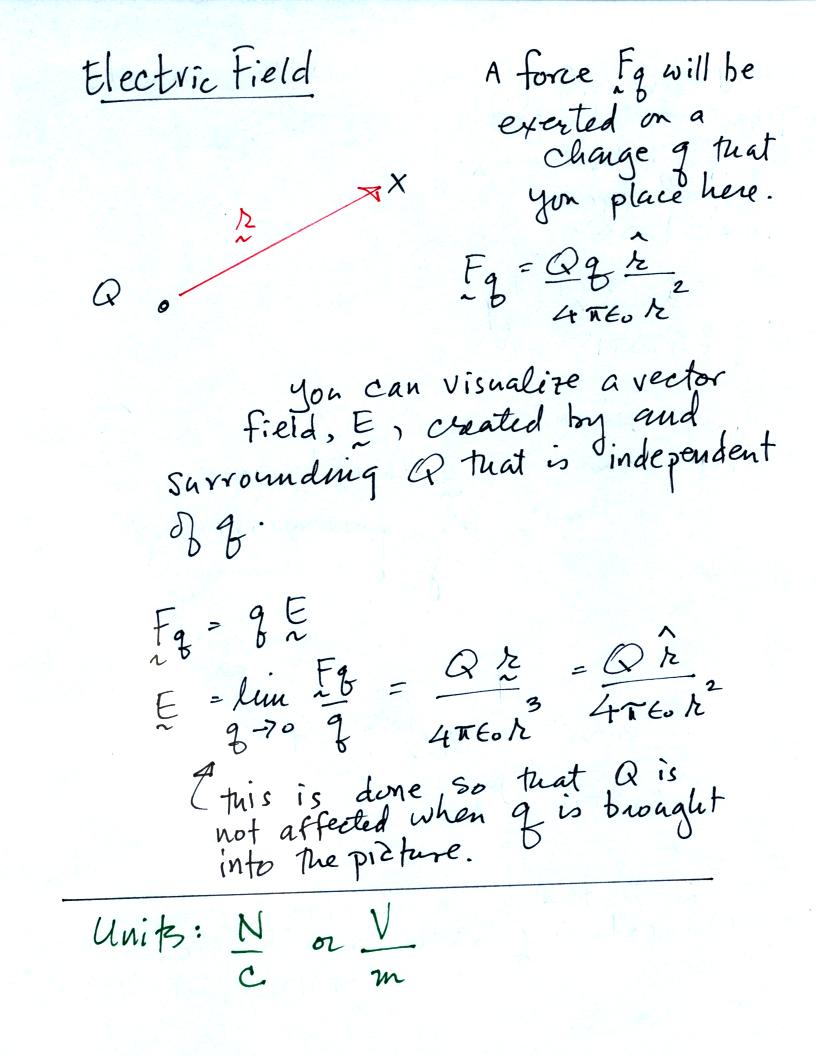
If a charge q is placed in the
vicinity of a charge Q, we could use Coulomb's law to determine the
force that Q exerts on q. We can imagine a vector field, the
electric field, existing around Q even before q is brought into the
picture. Multiplying q times E would give the force that Q exerts
on q. The expression for electric field is shown above.

Because the curl of the vector r
divided by r3 is zero, we can replace that term in the expression for
electric field with the gradient of 1/r.
This leads to a definition of the electrostatic potential.
It is often much simpler to determine the electrostatic potential
because it is a scalar quantity. The electric field can then be
determined by taking the gradient of the potential.
The expression above is valid for a point charge. More general
expressions for cases where multiple charges are present or when charge
is distributed over a volume or on a surface are shown below. This figure was not shown in class.
Essentially you would need to sum over a collection of multiple
charges, or integrate over volume and surface distributions of charge
to determine the electrostatic potential.

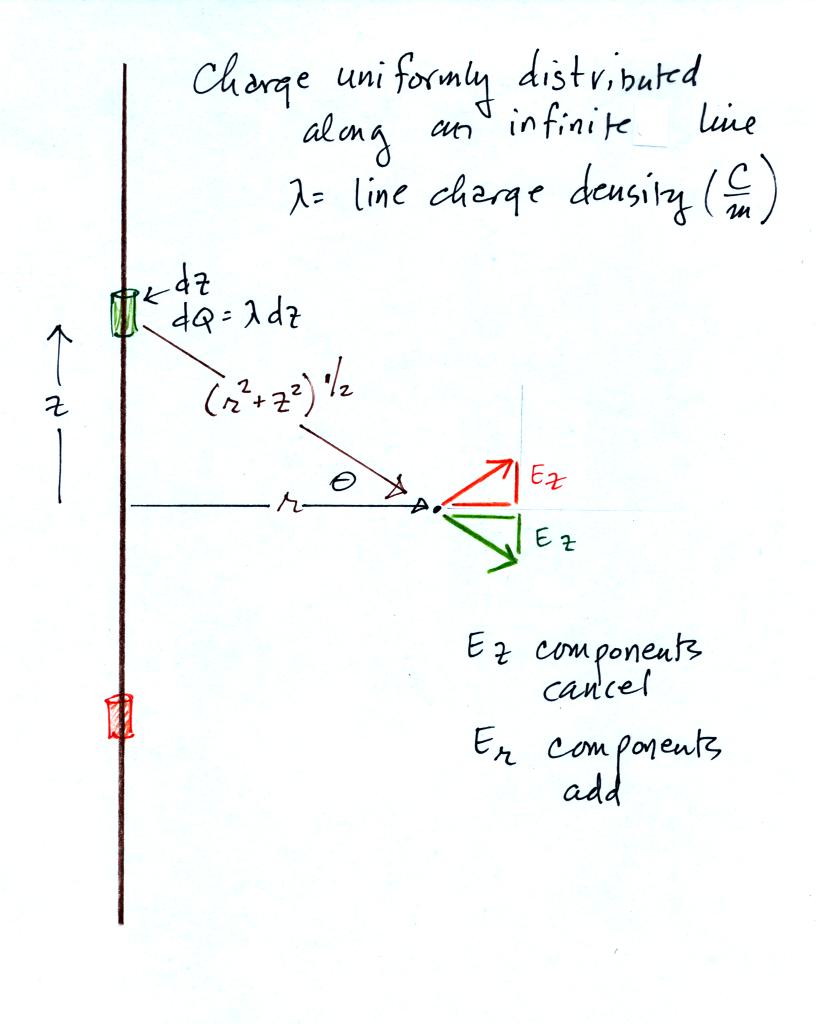
We'll try an example problem:
calculating the field a distance r away from an infinitely long line of
charge.
Short segments above and below z=0 contribute to the field.
The z components cancel, the r components add.
We'll come back to this problem and solve it in a much simpler way.
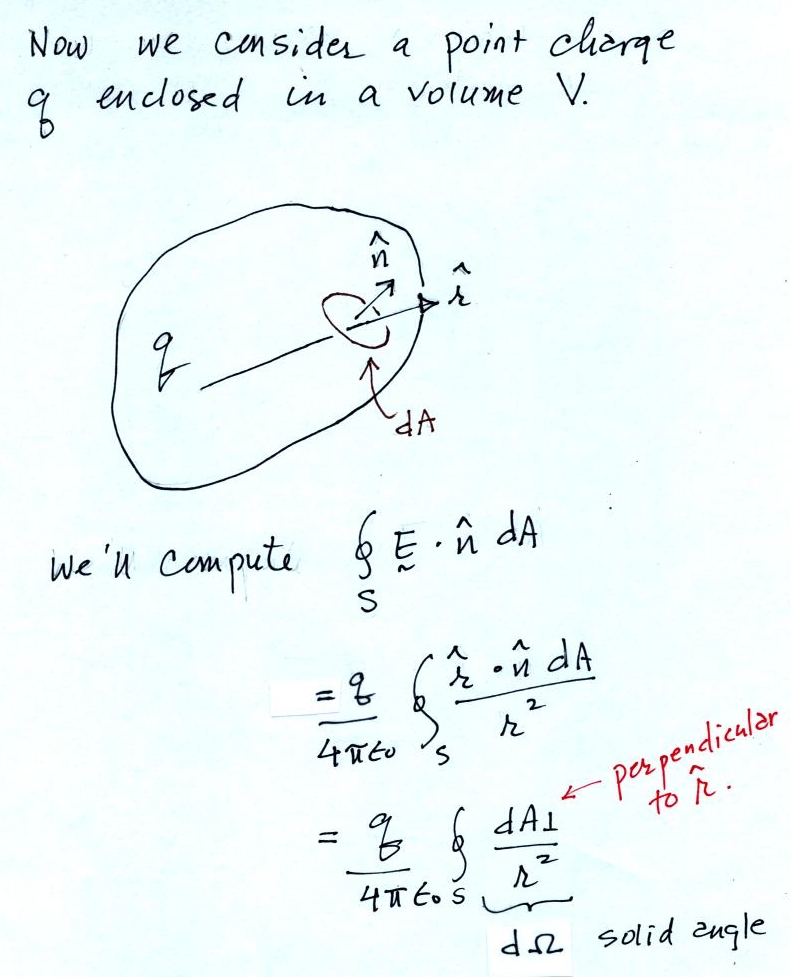
This is the integral form of Gauss' Law. We'll return to our
earlier problem and uses Gauss' Law to determine the electric
field. We'll see that it is a much easier process.
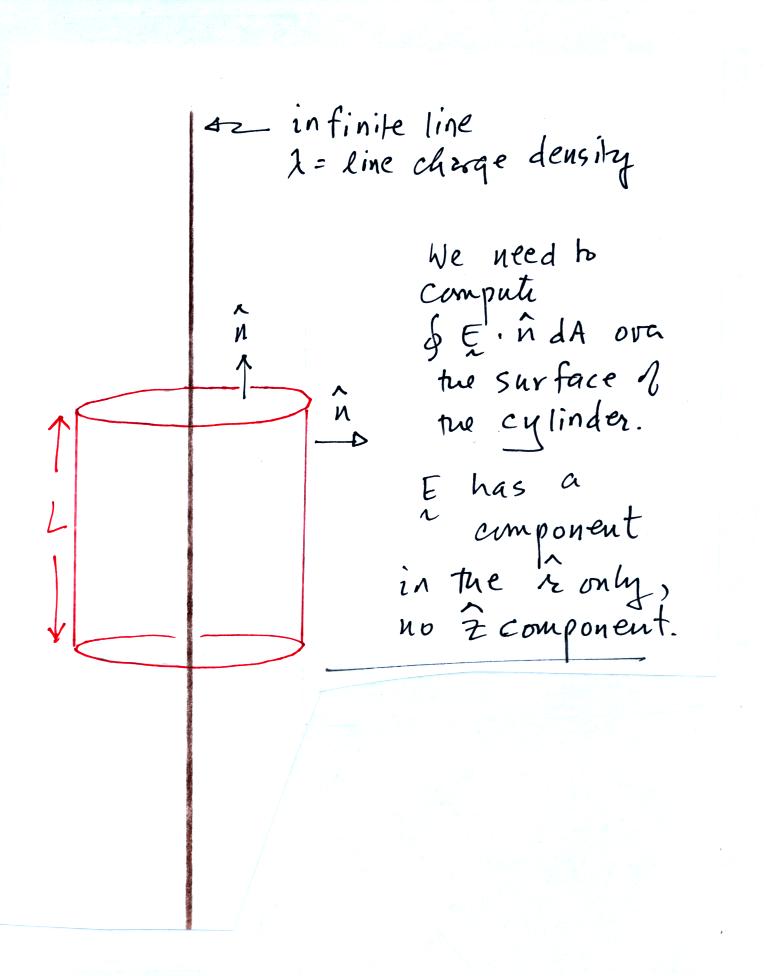
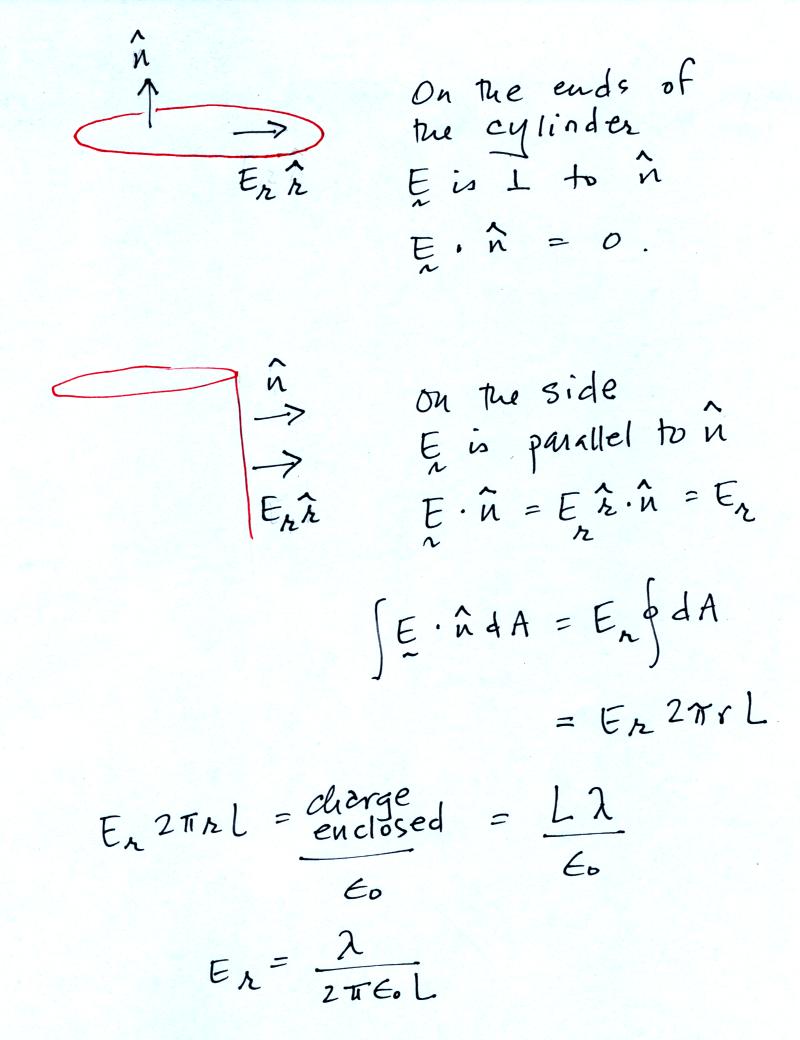
We draw a cylinder around the line of charge. This is the
area that we will integrate E over in the Gauss Law expression.
There is no contribution to the integral from the ends of the
cylinder (E is perpendicular to the normal vector, the dot product is
zero). E is parallel to the normal vector along the side of the
cylinder. E is also constant on the side of the cyliner (E is a
function of r and r stays constant as you integrate over the surface of
the cylinder side). In the end we obtain the same expression for
E as we did in the earlier example.
Here's a
little more detailed explanation of two of the demonstrations conducted
in class last Tuesday.
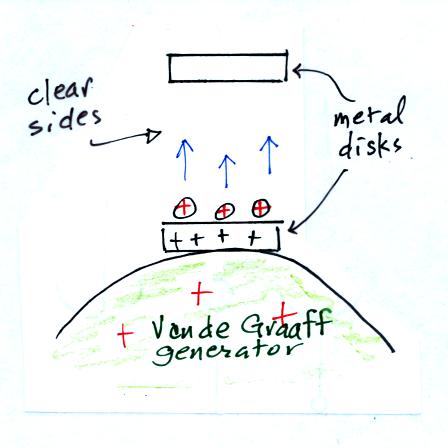
The Volta Hailstorm apparatus consisted of two metal disks mounted
above each other. They were mounted inside a clear plastic
cylinder. Small round balls made of aluminum foil
were inside. The apparatus was placed on top of a Van de Graaff
generator. The foil balls are in contact with the top
electrode and acquire some charge (assumed to be positive).
The balls are repelled by the bottom electrode and travel up to the top
metal disk. They transfer their charge to the top disk and then
fall back to the bottom disk.
The charge on the top disk bleeds off into the air through the
pieces of wire connected to the disk (the charge would eventually
travel to ground and complete the circuit). The foil balls again
acquire charge from the bottom disk and the whole process repeats
itself.
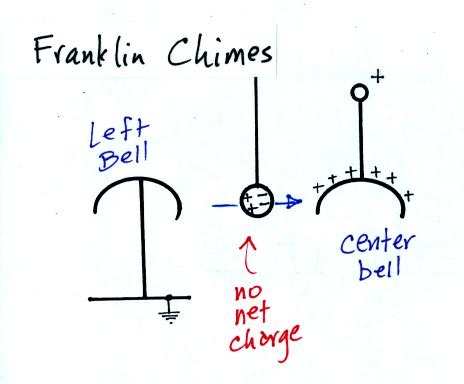
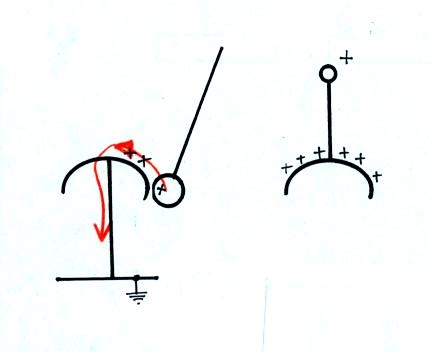
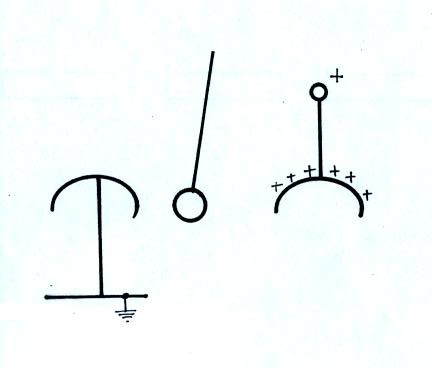
The Franklin chimes demonstration consisted of a center bell that
was connected to the Van De Graaff generator and bells to the right and
left that were grounded (only the left bell is shown in the figure
above). A small metal ball hung from an insulating thread between
the center bell and the left bell (and also between the center and
right bells). The small ball is assumed initially to be
uncharged. How ever the charged center bell will cause charges to
be induced on the surface of the ball as shown in the figure (these
charges make the electric field inside the ball zero). The ball
will be drawn toward the center bell.
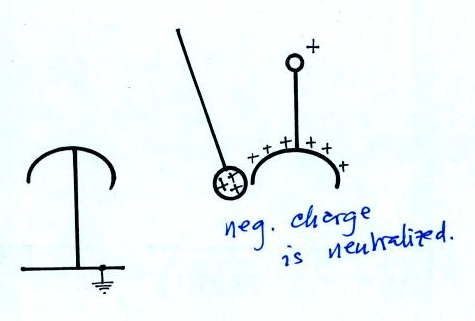
Once the ball contacts the center bell, the negative charge is
neutralized. The positively charged ball is repelled by the
center bell.
Once the ball touches the grounded bell, the positive charge flows to
ground.
The ball is again uncharged. The whole process repeats
itself. The motion of the ball is transporting charge from the
center bell (i.e. from the Van de Graaff generator ) to ground.