Tuesday Mar. 24, 2009

The midterm exams were returned in class today together with a set of solutions (the answer to Question #5 will come in a later handout).  The average score for undergraduates was 35 out of 40 (87.5%) and for graduate students was 46.5 out of 50 (93%).  Homework assignment #4 will be returned in class on Thursday together with a midterm grade summary.
Over the next couple of classes we will be learning how certain lightning return stroke current characteristics can be estimated from remote measurements of electric and magnetic fields radiated by lightning.  This will first involve learning something about the fields radiated by lightning and about return stroke currents vary with time and altitude along the lightning channel.

The expression above gives the magnetic field radiated by a short segment dz located at an altitude z above the ground. The lightning channel is assumed to straight and vertical.  The ground is assumed to be a perfect conductor.  This expression was on a class handout.  The two direction vector symbols highlighted in yellow were inadvertently left off the expression on the handout.


Here is the expression for the electric field.  The highlighted symbols were accidently left off the expressions on the class handout.  These expressions are from the following publication:
Uman, M.A., D.K. McLain, and E.P. Krider, "The Electromagnetic Radiation from a Finite Antenna," Am. J. Phys., 43, 33-38, 1975.

The equations above actually aren't quite correct.  The two figures below are from a later publication that gave the correct expressions.

A figure showing the channel geometry and defining some of the variables is shown below.


We won't be using any of these rather complex general expressions.  Rather let's just note that the electric field expression contains terms involving a time integral of current, the current itself, and a term with the time derivative of the current.
This is summarized in the figure below.

The electrostatic field component is dominant near the discharge.  The radiation field term is dominant very early in the discharge and also far from the discharge.


Representative examples of E field waveshapes at various distances from a lightning strike.


The magnetic field contains only radiation and induction field components.
We don't really know what I(z,t) is in a lightning channel.  The lightning current can be measured at the ground in triggered lightning and in strikes to instrumented towers, so we do sometimes know I(0,t).


Listed above are some of the approaches that have been taken to try to determine I(z,t).  We will mostly be concerned with the 3rd approach.

Here is one of the first experimental approaches aimed at determining the relationship between fields and channel current.   First you make simultaneous measurements of  E and B fields at two stations, one close to and the other far from a lightning strike.  You make some assumptions concerning I(z,t) (we'll look at a couple of examples) and then use the far field measurement (radiation field component only) to infer I(z,t).  Then using I(z,t) and the general expression for E fields (given earlier in class) calculate the close field and compare that with the measured field.

Bruce Golde Model

In the Bruce Golde model the return stroke current is assumed to be uniform along the length of the channel.  The lightning current changes with time but there is no variation along the length of the channel.  This is illustrated in the figure below.

The current waveform measured at the ground is shown at the bottom of the figure.  Current amplitude along the length of the channel is shown above.  As current changes at the ground, it also changes simultaneously along the entire length of the channel.  This is physically unreasonable as it would require that information propagate along the length of the channel at infinite speed.

Here is first an expression for the radiation field component of the electric field at a distance D from the lightning stroke.  This can be inverted to give the channel base current as a function of the measured field.

Transmission Line Model


In the transmission line model the current waveform measured at the ground is assumed to propagate up the channel without changing shape and at constant speed.



The first equation below shows how I varies with time and altitude.
\
The second equation gives the radiation field component of the E field.   We will see that the time derivation of current (I) can be replaced with a derivative with respect to z.


This leads to a very simple relationship between channel current and the electric radiation field.


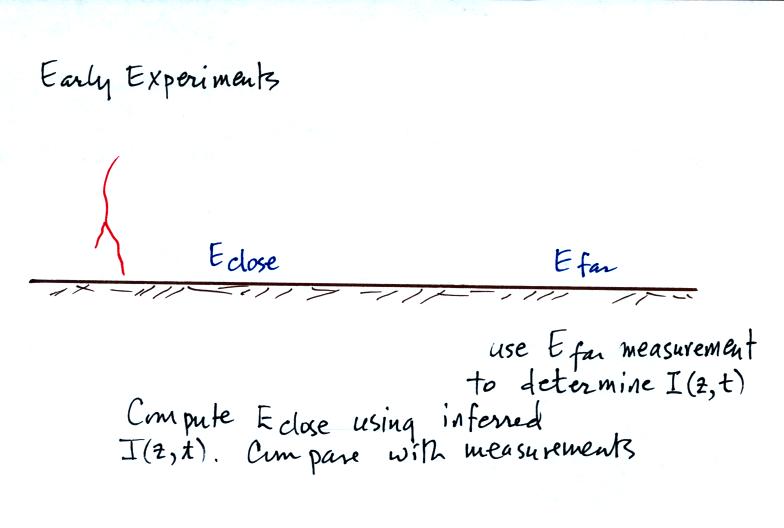
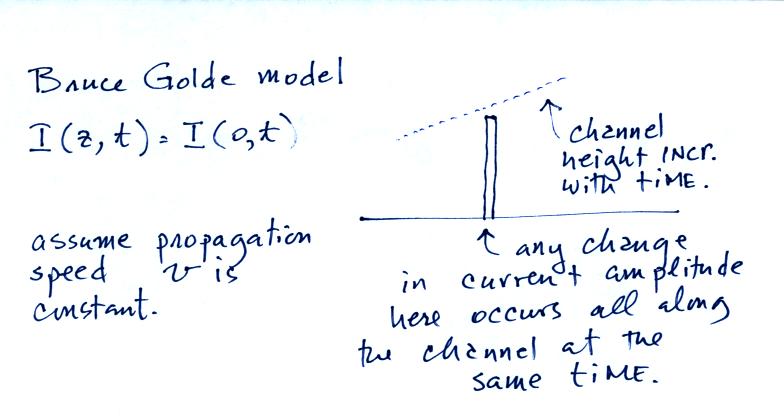
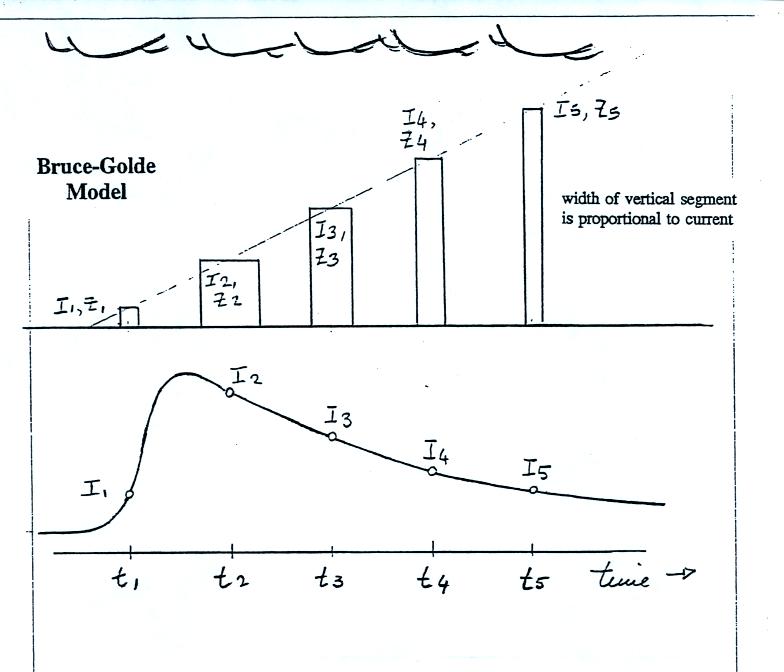
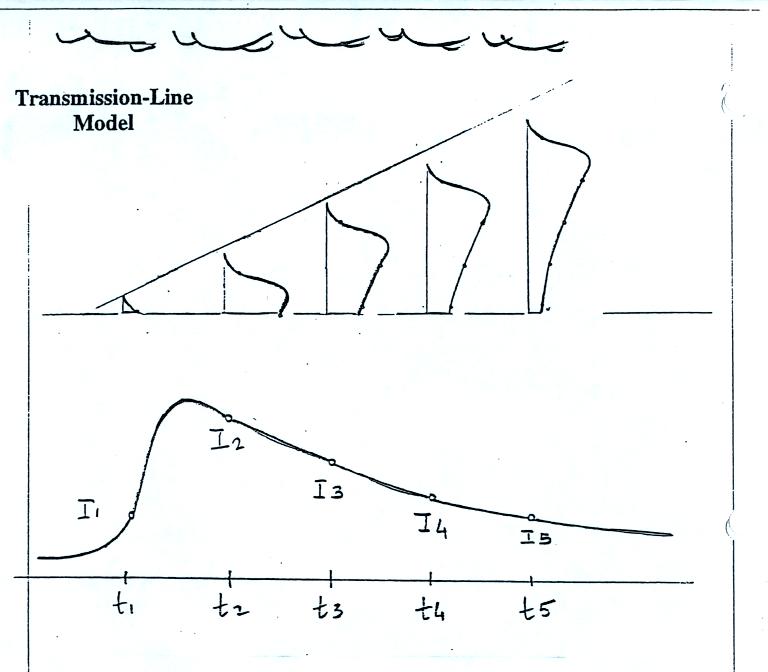
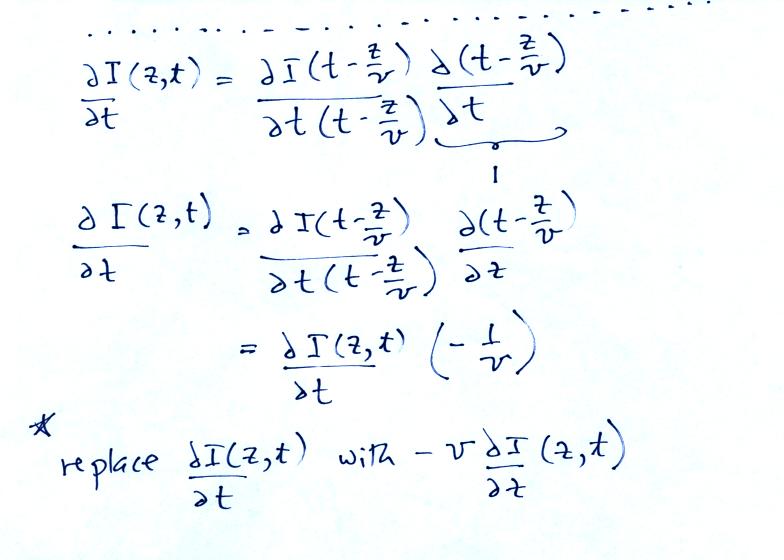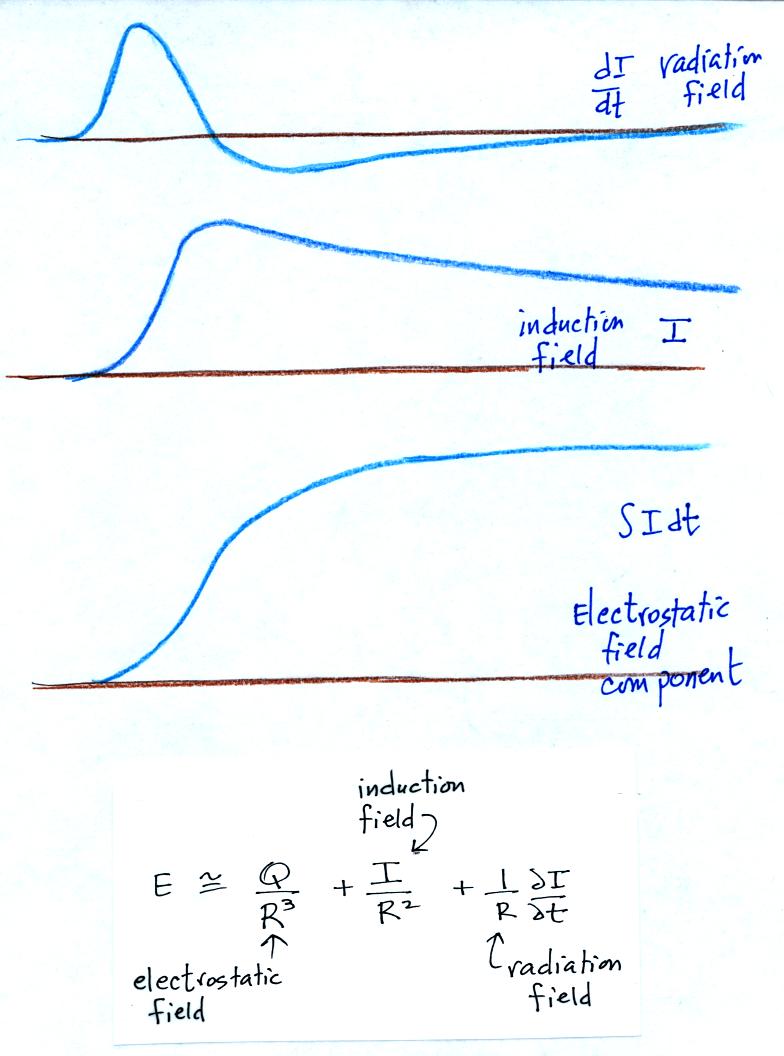
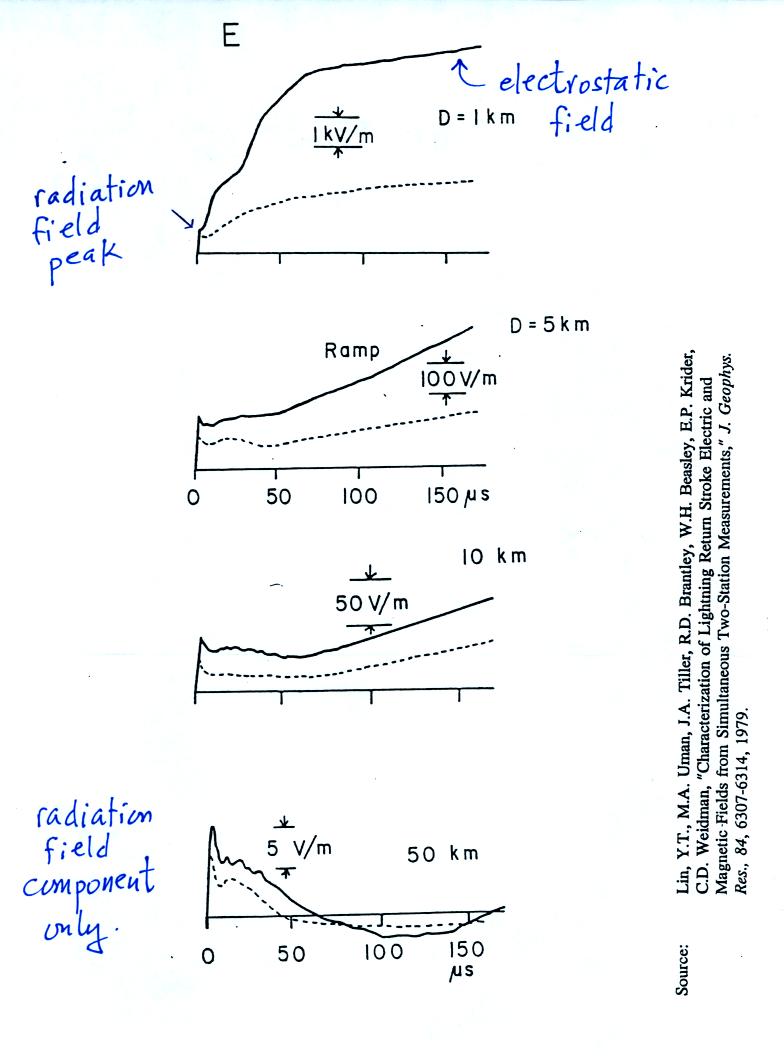
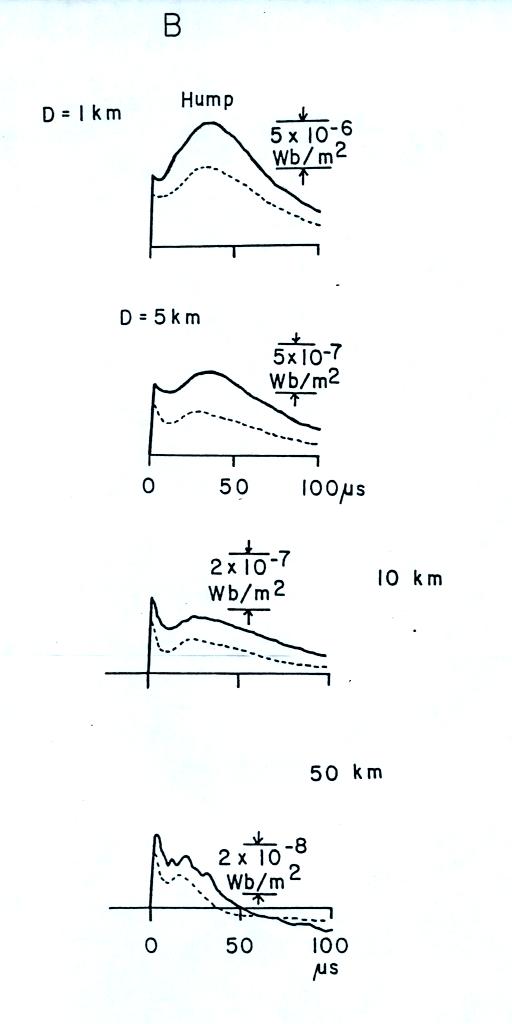
We will look at some of the results from experimental tests of the Bruce Golde and Transmission Line models in the next class.  We will also look at some estimates of peak return stroke current and current derivative that have been derived from remote measurements of E and dE/dt.
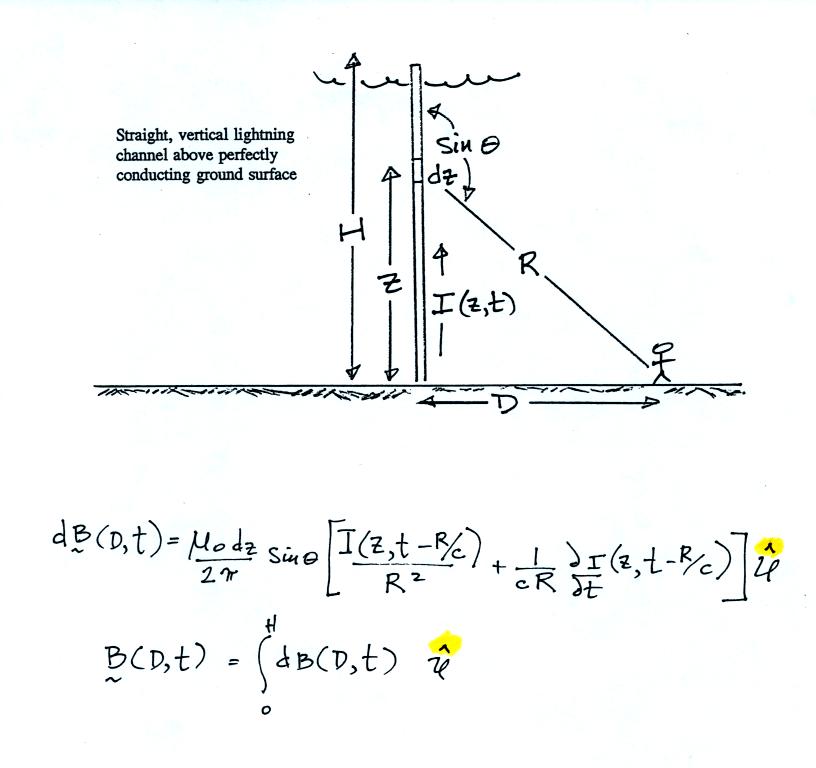
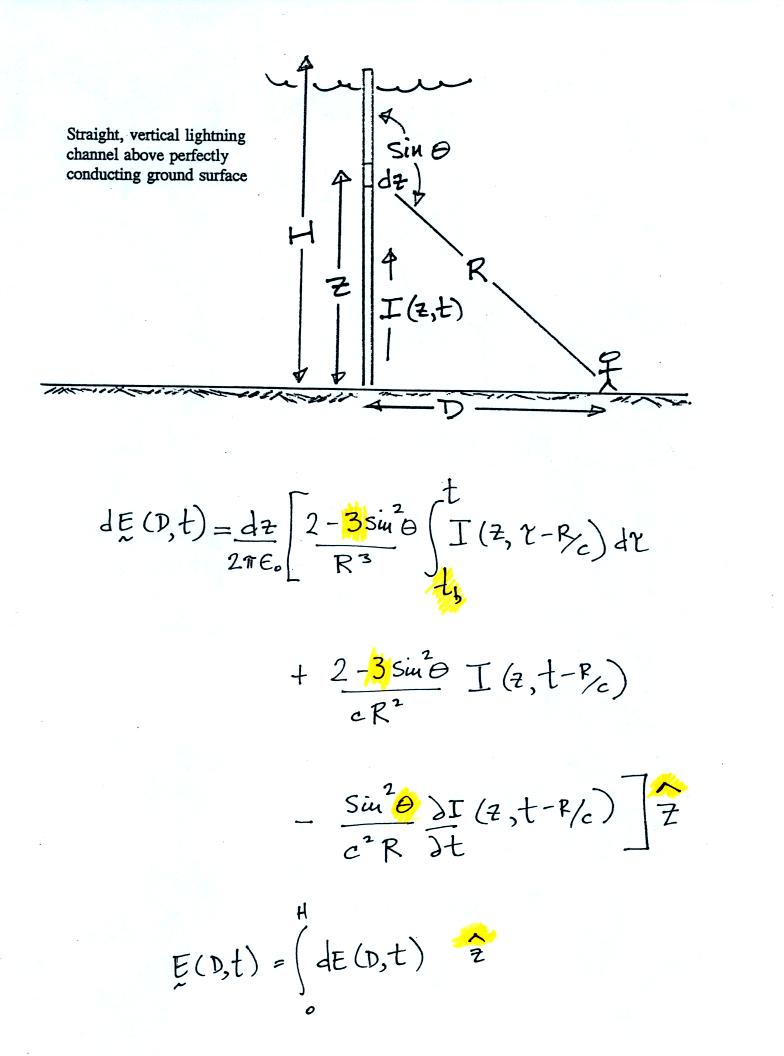
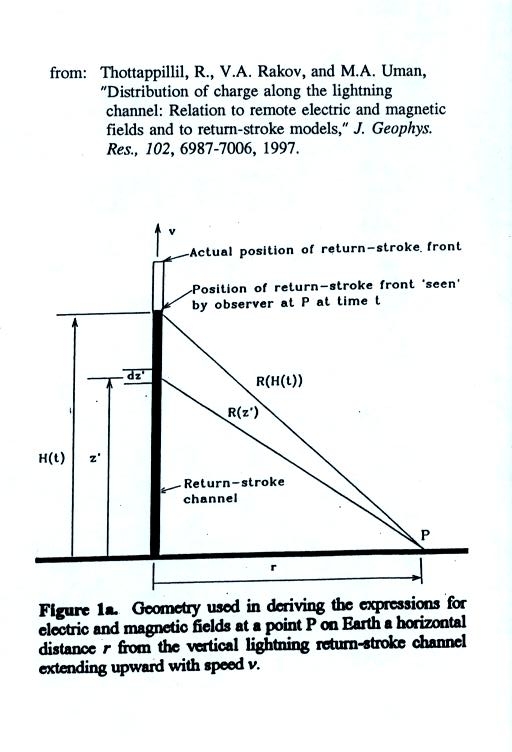
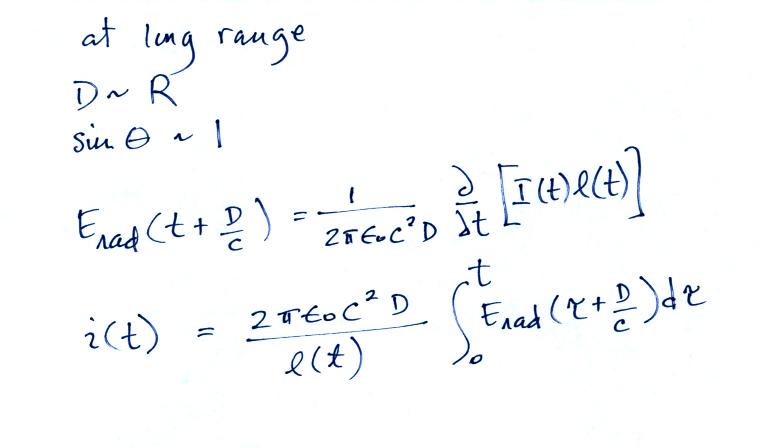
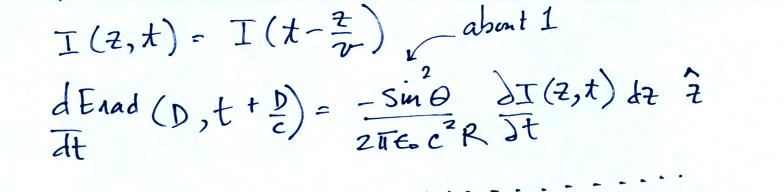