This is
Rajah, one of my two cats.

Rajah likes to help grade papers (looks like lab reports in
this case). The rain on Sunday meant he had muddy feet.

This is my other cat, Fox. She's defending a bush of
catnip that grows like a weed in my vegetable garden.
Before the quiz last week we saw how the relative strengths of the downward graviational force and the upward pressure difference force determine whether a parcel of air will rise or sink. Archimedes Law is another way of trying to understand this topic.

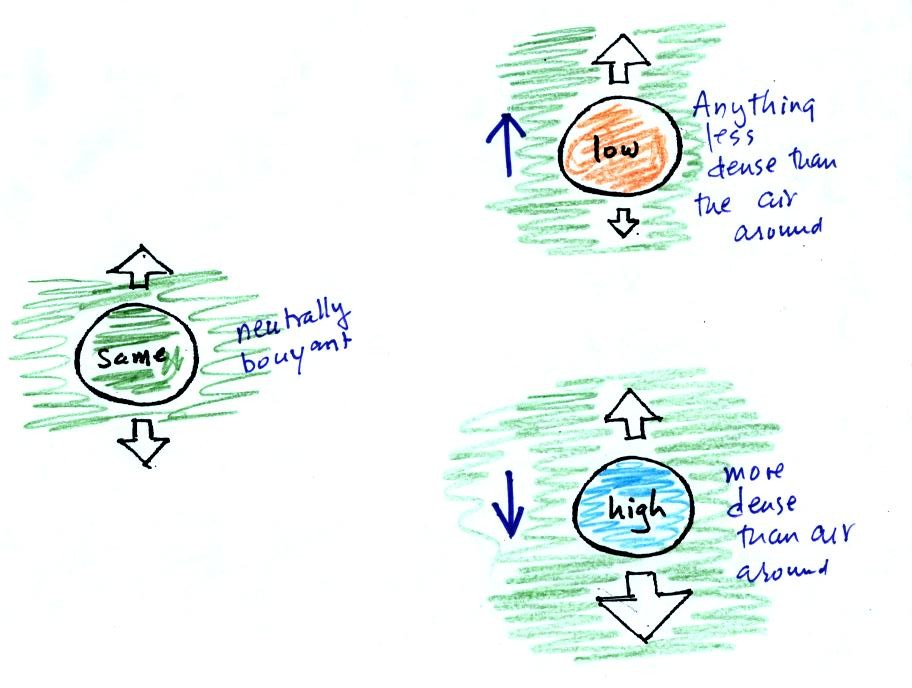

Before the quiz last week we saw how the relative strengths of the downward graviational force and the upward pressure difference force determine whether a parcel of air will rise or sink. Archimedes Law is another way of trying to understand this topic.

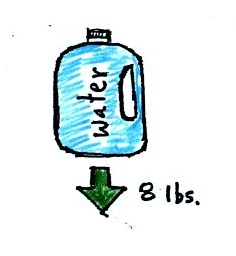
A gallon of
water weighs about 8 pounds (lbs).
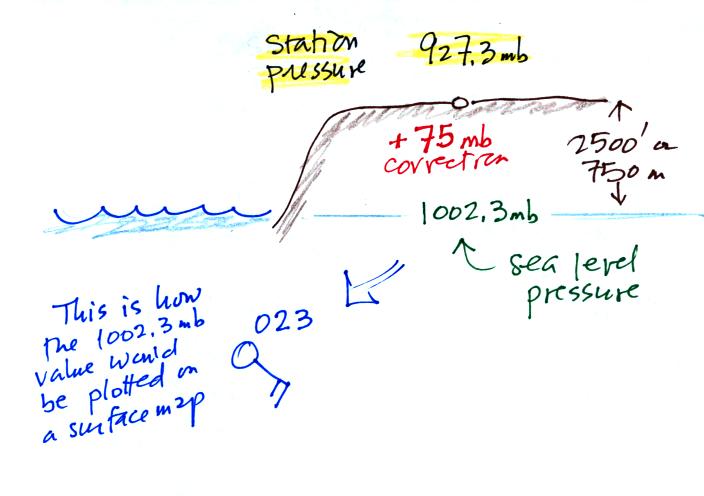
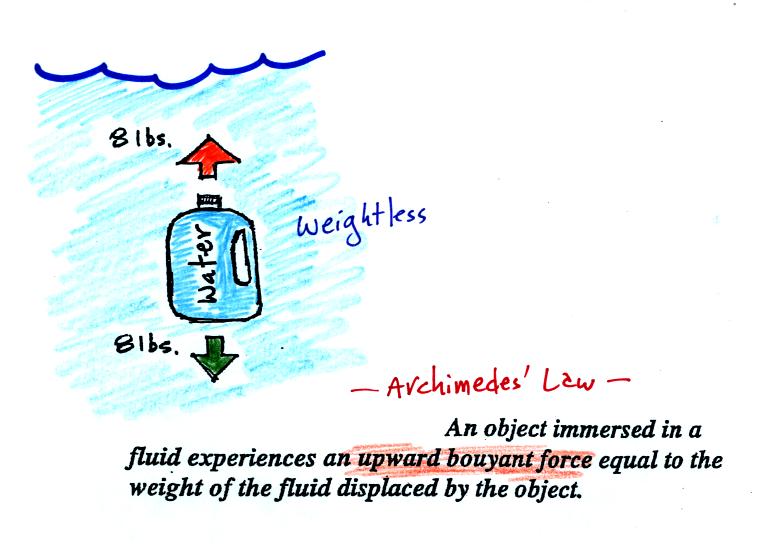
If you submerge a 1 gallon jug of water in a swimming pool, an amazing thing happens - the jug becomes, for all intents and purposes, weightless. Archimedes' Law (see figure below, from p. 53a in the photocopied ClassNotes) explains why this is true.
If you submerge a 1 gallon jug of water in a swimming pool, an amazing thing happens - the jug becomes, for all intents and purposes, weightless. Archimedes' Law (see figure below, from p. 53a in the photocopied ClassNotes) explains why this is true.

The upward bouyant
force is
really
just another name for the
pressure difference force covered earlier today (higher pressure
pushing
up on the bottle and low pressure at the top pushing down, resulting in
a net upward force). A 1 gallon bottle will displace 1 gallon of
pool water. One
gallon of pool
water weighs 8 pounds. The upward bouyant force will be 8 pounds,
the same as the downward force on the jug due to gravity. The two
forces are equal and opposite.
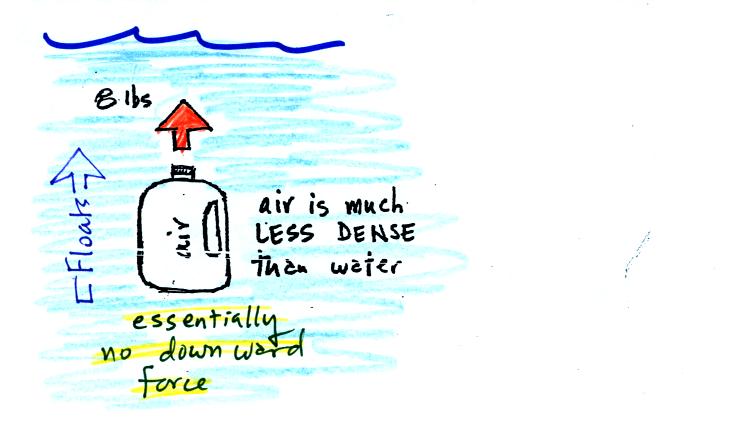
Now we imagine pouring out all the water and filling the 1 gallon jug with air. Air is about 1000 times less dense than water;compared to water, the jug will weigh practically nothing.
Now we imagine pouring out all the water and filling the 1 gallon jug with air. Air is about 1000 times less dense than water;compared to water, the jug will weigh practically nothing.

If you submerge the jug in a
pool
it will displace 1 gallon of
water
and experience an 8 pound upward bouyant force again. Since there
is no downward force the jug will float.
One gallon of sand (which is about 1.5 times denser than water) jug will weigh 12 pounds.
One gallon of sand (which is about 1.5 times denser than water) jug will weigh 12 pounds.

The jug of sand will sink
because
the downward force is greater
than
the upward force.
You can sum all of this up by saying anything that is less dense than water will float in water, anything that is more dense than water will float in water.
The same reasoning applies to air in the atmosphere.
You can sum all of this up by saying anything that is less dense than water will float in water, anything that is more dense than water will float in water.
The same reasoning applies to air in the atmosphere.

Air that is less dense
(warmer)
than the air around it will
rise.
Air that is more dense (colder) than the air around it will sink.
Here's a little more information about Archimedes.
There's a colorful demonstration how small differences in density can determine whether an object floats or sinks.

A can of regular Coca Cola (which now has the exclusive franchise
on the U. of A. campus, the figure above was drawn when Pepsi had the
franchise) was placed in a beaker of water.
The
can
sank. A can of Diet Coke on the other hand floated.
Both cans are made of aluminum which has a density almost three times higher than water. The drink itself is largely water. The regular Pepsi also has a lot of high-fructose corn syrup, the diet Pepsi doesn't. The mixture of water and corn syrup has a density greater than plain water. There is also a little air (or perhaps carbon dioxide gas) in each can.
The average density of the can of regular Pepsi (water & corn syrup + aluminum + air) ends up being slightly greater than the density of water. The average density of the can of diet Pepsi (water + aluminum + air) is slightly less than the density of water.
We repeated the demonstration with a can of Pabst Blue Ribbon beer. That also floated, the beer doesn't contain any corn syrup.
In some respects people in swimming pools are like cans of regular and diet soda. Some people float (they're a little less dense than water), other people sink (slightly more dense than water).

Many people can fill their lungs with air and make themselves
float, or
they can empty their lungs and make themselves sink.
People must have a density that is about the same as water.
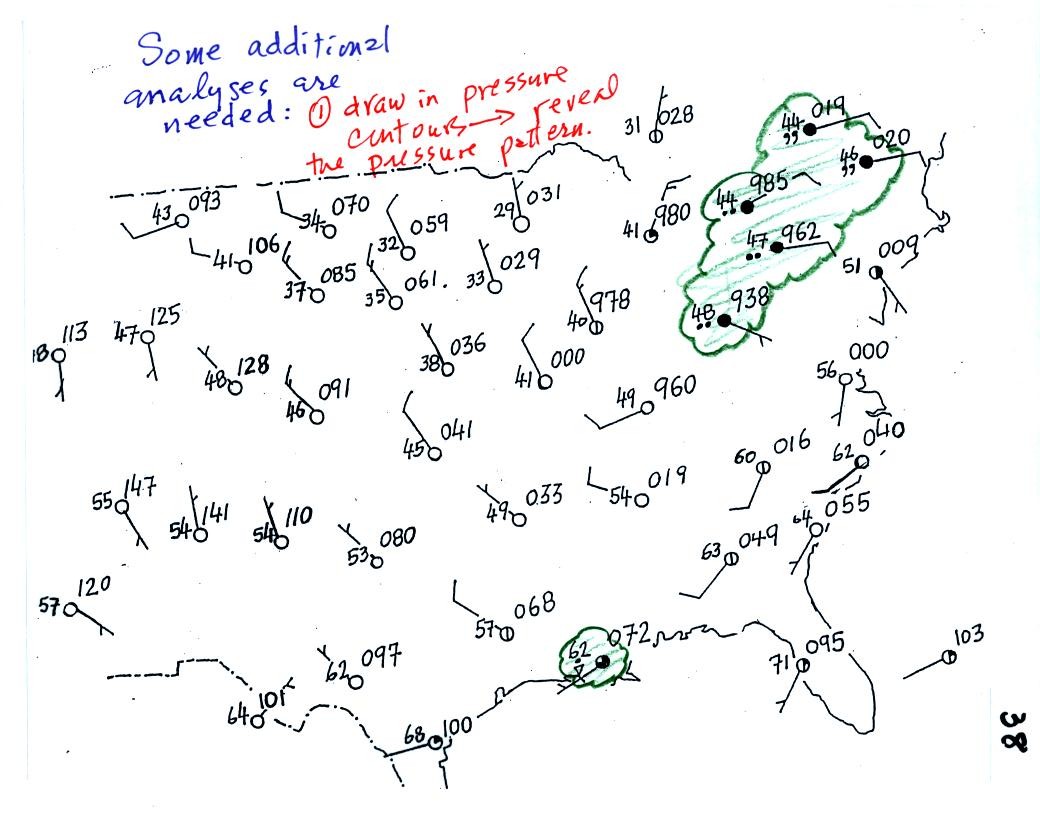
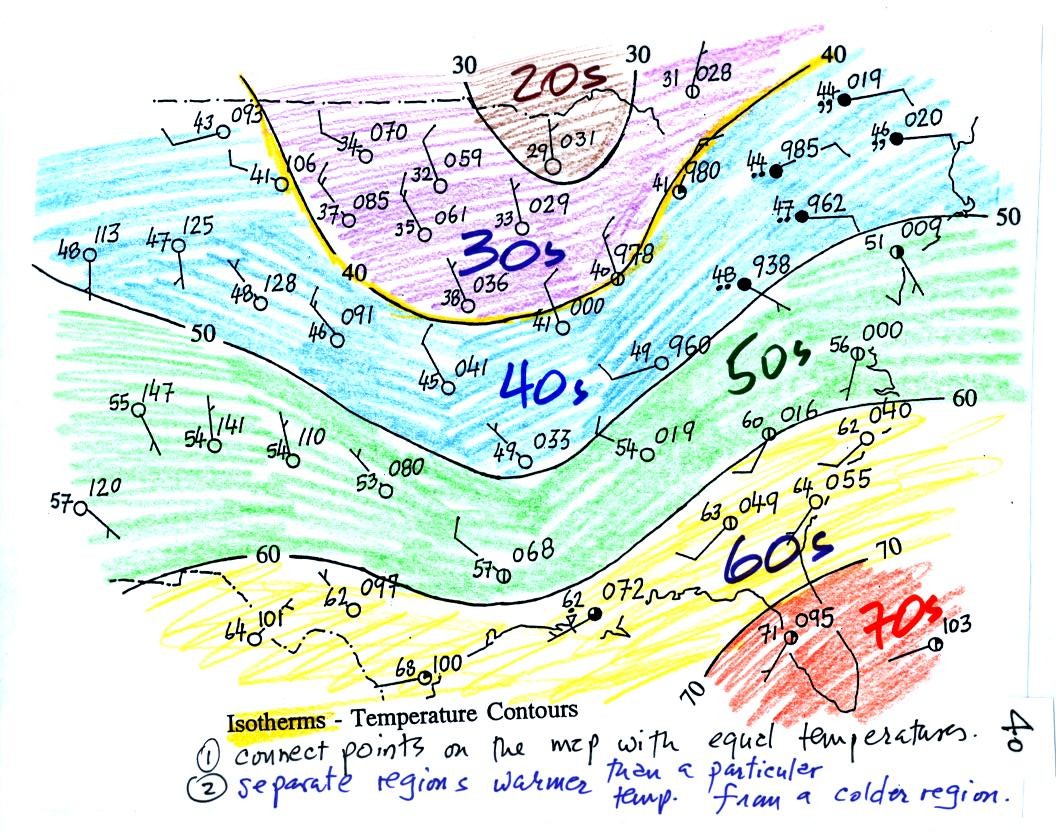
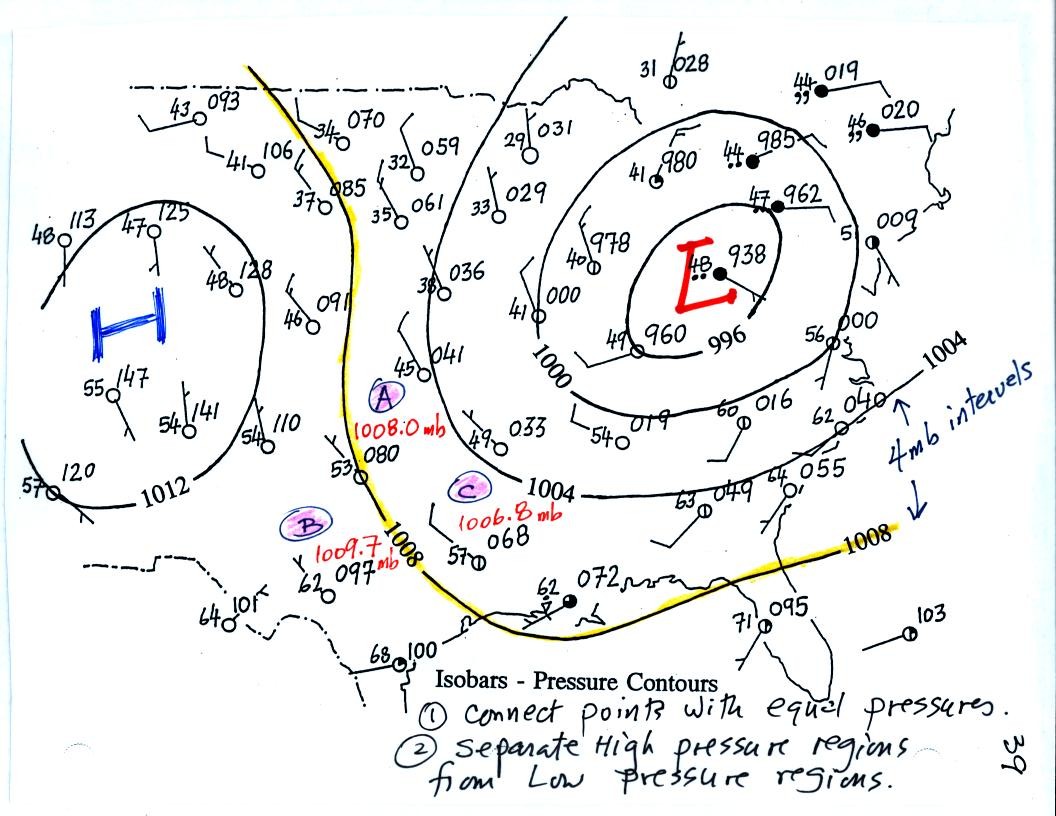
We spent the remainder of the day on a new topic - Surface Weather Maps. We began by learning how weather data are entered onto surface weather maps.
Much of our weather is produced by relatively large (synoptic scale) weather systems. To be able to identify and characterize these weather systems you must first collect weather data (temperature, pressure, wind direction and speed, dew point, cloud cover, etc) from stations across the country and plot the data on a map. The large amount of data requires that the information be plotted in a clear and compact way. The station model notation is what meterologists use.
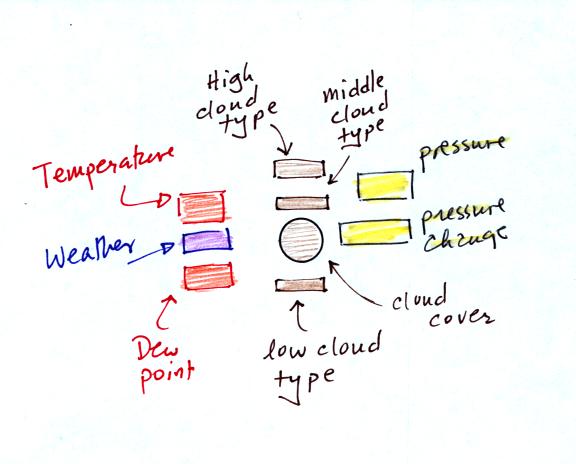
The figure
above wasn't
shown in class.
A small circle is plotted on the map at the location where the weather measurements were made. The circle can be filled in to indicate the amount of cloud cover. Positions are reserved above and below the center circle for special symbols that represent different types of high, middle, and low altitude clouds. The air temperature and dew point temperature are entered to the upper left and lower left of the circle respectively. A symbol indicating the current weather (if any) is plotted to the left of the circle in between the temperature and the dew point; you can choose from close to 100 different weather symbols (on a handout distributed in class). The pressure is plotted to the upper right of the circle and the pressure change (that has occurred in the past 3 hours) is plotted to the right of the circle.
So we'll work through this material one step at a time (refer to p. 36 in the photocopied ClassNotes). Some of the figures below were borrowed from a previous semester or were redrawn and may differ somewhat from what was drawn in class.
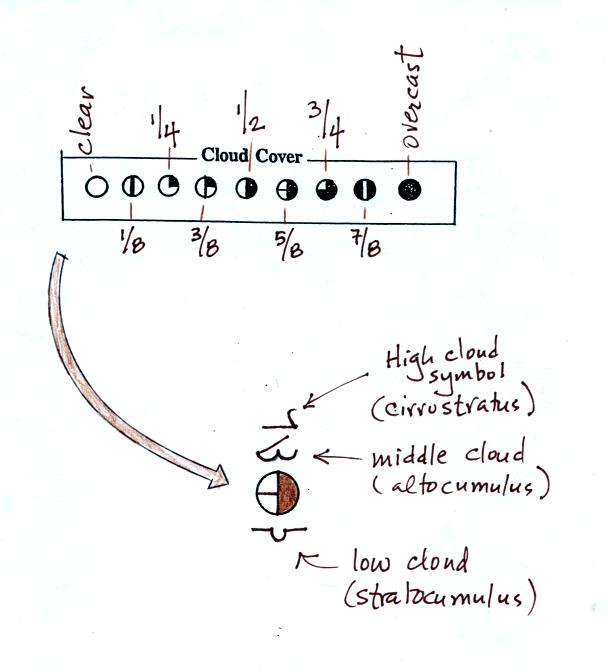
The center circle is filled in to indicate the portion
of
the sky
covered with clouds (estimated to the nearest 1/8th of the sky) using
the code at the top of the figure. 3/8ths of the sky is covered
with clouds in the example above. Then symbols (not drawn in class)
are
used
to
identify
the
actual types of high, middle, and low altitude clouds (the
symbols can be found on the handout to be distributed in class).
In (a) the winds are from the NE at 5 knots, in (b) from the SW at 15 knots, in (c) from the NW at 20 knots, and in (d) the winds are from the NE at 1 to 2 knots.
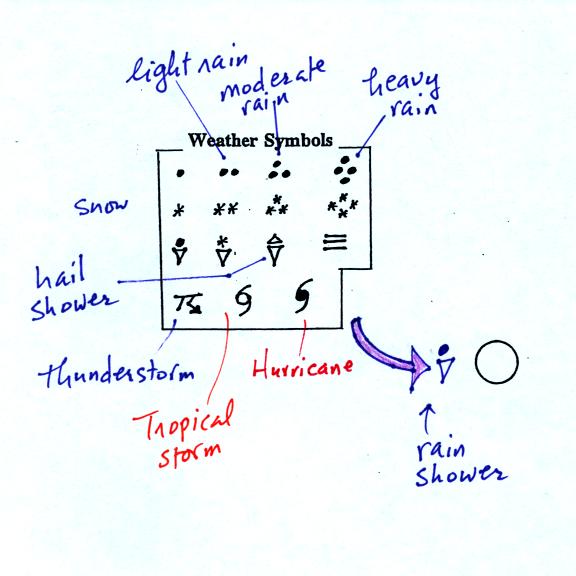
A symbol representing the weather that is currently occurring is plotted to the left of the center circle (in between the temperature and the dew point). Some of the common weather symbols are shown. There are about 100 different weather symbols that you can choose from (these weather symbols were on the handout distributed in class)
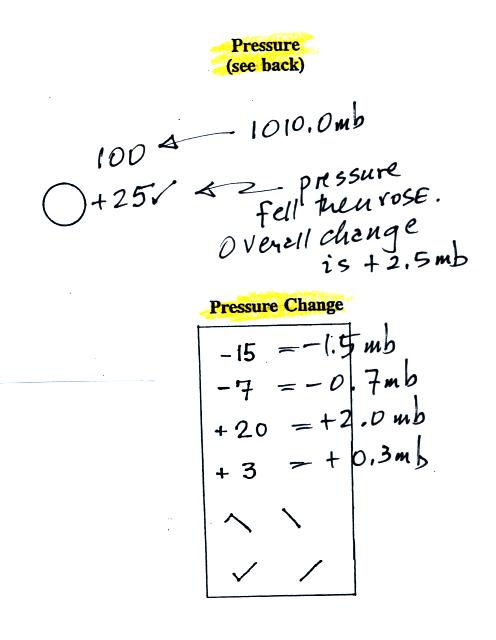
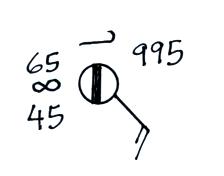
The sea level pressure is shown above and to the right of the center circle. Decoding this data is a little "trickier" because some information is missing. We'll look at this in more detail momentarily.
Pressure change data (how the pressure has changed during the preceding 3 hours and not covered in class) is shown to the right of the center circle. You must remember to add a decimal point. Pressure changes are usually pretty small.
Here are some links to surface weather maps with data plotted using the station model notation: UA Atmos. Sci. Dept. Wx page, National Weather Service Hydrometeorological Prediction Center, American Meteorological Society.
An In-class Optional Assignment was given during class and collected at the end of the period. If you are reading the online notes and weren't in class, you can answer the two questions and turn in the assignment before class on Thursday for credit. Here are the two questions.
Question #1
Air that is more dense (colder) than the air around it will sink.
Here's a little more information about Archimedes.
There's a colorful demonstration how small differences in density can determine whether an object floats or sinks.

Both cans are made of aluminum which has a density almost three times higher than water. The drink itself is largely water. The regular Pepsi also has a lot of high-fructose corn syrup, the diet Pepsi doesn't. The mixture of water and corn syrup has a density greater than plain water. There is also a little air (or perhaps carbon dioxide gas) in each can.
The average density of the can of regular Pepsi (water & corn syrup + aluminum + air) ends up being slightly greater than the density of water. The average density of the can of diet Pepsi (water + aluminum + air) is slightly less than the density of water.
We repeated the demonstration with a can of Pabst Blue Ribbon beer. That also floated, the beer doesn't contain any corn syrup.
In some respects people in swimming pools are like cans of regular and diet soda. Some people float (they're a little less dense than water), other people sink (slightly more dense than water).

People must have a density that is about the same as water.
We spent the remainder of the day on a new topic - Surface Weather Maps. We began by learning how weather data are entered onto surface weather maps.
Much of our weather is produced by relatively large (synoptic scale) weather systems. To be able to identify and characterize these weather systems you must first collect weather data (temperature, pressure, wind direction and speed, dew point, cloud cover, etc) from stations across the country and plot the data on a map. The large amount of data requires that the information be plotted in a clear and compact way. The station model notation is what meterologists use.

A small circle is plotted on the map at the location where the weather measurements were made. The circle can be filled in to indicate the amount of cloud cover. Positions are reserved above and below the center circle for special symbols that represent different types of high, middle, and low altitude clouds. The air temperature and dew point temperature are entered to the upper left and lower left of the circle respectively. A symbol indicating the current weather (if any) is plotted to the left of the circle in between the temperature and the dew point; you can choose from close to 100 different weather symbols (on a handout distributed in class). The pressure is plotted to the upper right of the circle and the pressure change (that has occurred in the past 3 hours) is plotted to the right of the circle.
So we'll work through this material one step at a time (refer to p. 36 in the photocopied ClassNotes). Some of the figures below were borrowed from a previous semester or were redrawn and may differ somewhat from what was drawn in class.


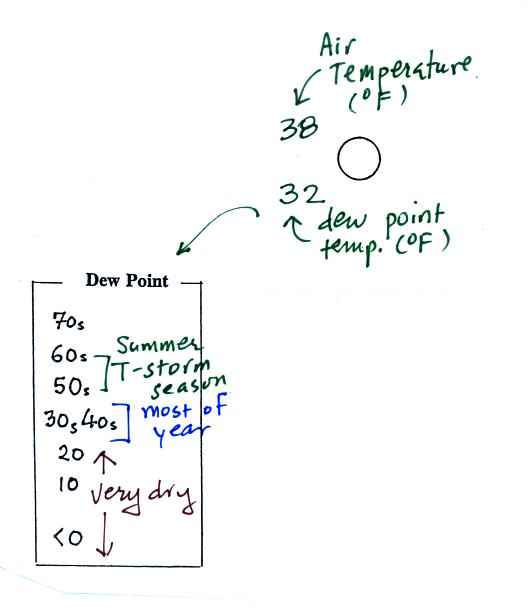
The air temperature in this example
was 38o
F
(this is
plotted above and to the left of the center circle). The dew
point
temperature was 32o F and is plotted below and to the left
of the center circle. The box at lower left reminds you that dew
points range from the mid 20s to the mid 40s during much of the year in
Tucson.
Dew
points rise into the upper 50s and 60s during the summer thunderstorm
season (dew points are in the 70s in many parts of the country in the
summer). Dew points are in the 20s, 10s, and may even drop below
0 during dry periods in Tucson.

A straight line extending out from the center circle
shows the wind direction. Meteorologists always give the
direction the wind is coming from.
In this example the winds are
blowing from the SE toward the NW at a speed of 10 knots (SE winds in
the top part of the figure, the wind examples in the bottom part are
coming from the south). A
meteorologist would call
these southeasterly winds. Small barbs at the end of the straight
line give the wind speed in knots. Each long barb is worth 10
knots, the short barb is 5 knots.
Knots are nautical miles per hour. One nautical mile per hour is
1.15 statute miles per hour. We won't worry about the distinction
in this class, you can just pretend that one knot is the same as one
mile per hour.
Here are some additional wind examples that weren't shown in class:
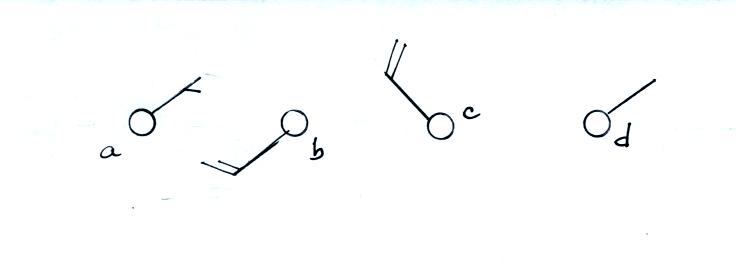

Here are some additional wind examples that weren't shown in class:

In (a) the winds are from the NE at 5 knots, in (b) from the SW at 15 knots, in (c) from the NW at 20 knots, and in (d) the winds are from the NE at 1 to 2 knots.

A symbol representing the weather that is currently occurring is plotted to the left of the center circle (in between the temperature and the dew point). Some of the common weather symbols are shown. There are about 100 different weather symbols that you can choose from (these weather symbols were on the handout distributed in class)

The sea level pressure is shown above and to the right of the center circle. Decoding this data is a little "trickier" because some information is missing. We'll look at this in more detail momentarily.
Pressure change data (how the pressure has changed during the preceding 3 hours and not covered in class) is shown to the right of the center circle. You must remember to add a decimal point. Pressure changes are usually pretty small.
Here are some links to surface weather maps with data plotted using the station model notation: UA Atmos. Sci. Dept. Wx page, National Weather Service Hydrometeorological Prediction Center, American Meteorological Society.
An In-class Optional Assignment was given during class and collected at the end of the period. If you are reading the online notes and weren't in class, you can answer the two questions and turn in the assignment before class on Thursday for credit. Here are the two questions.
Question #1