Tue., Feb. 23, 2010
click here to download today's notes in a more printer friendly format

A couple of Bob Dylan songs ("Like a Rolling Stone" and "Stuck in Mobile with the Memphis Blues Again") before class today.

Quiz #1 was returned in class today.  This quiz counts so you should carefully check to be sure the grading was done correctly and that the points were added up correctly.  If you didn't do as well as you thought you should have there is still plenty of time to turn things around before the end of the semester.  I would suggest you stop by sometime during office hours to discuss what I think are effective quiz study strategies.

The 1S1P radon reports were also returned today.

The Experiment #2 reports are due next week.  You should try to return the materials and pick up the supplementary information sheet this week.
For the next couple of weeks or so we will be learning about several different forms of energy, energy transport, and the atmospheric greenhouse effect.  It is easy to get wrapped up in all the details so class started with a little bit of  an introduction to this new topic.

When you add energy to an object, the object will usually warm up (conversely when you take energy from an object the object will cool).  It is relatively easy to come up with an equation that allows you to figure out what the temperature change will be.



The temperature change will first depend on how much energy was added.  This is a direct proportionality, so delta E is in the numerator of the equation (delta E and delta T are both positive when energy is added, negative when energy is taken from something)

When you add equal amounts of energy to large and small  pans of water, the small pan will heat up more quickly.  The temperature change, delta T, will depend on the mass.  A small mass will mean a large delta T, so mass should go in the denominator of the equation.  

Different materials react differently when energy is added to them.  A material with a large specific heat will warm more slowly than a material with a small specific heat.  Specific heat has the same kind of effect on delta T as mass.  Specific heat is sometimes called "thermal mass" or "thermal capacity."

Here's an important example that will show the effect of specific heat (middle of p. 45)



Equal amounts of energy (1000 calories, note that calories are units of energy) are added to equal masses (500 grams) of water and soil.  We use water and soil in the example because most of the earth's surface is either ocean or land. Water has a higher specific heat than soil, it only warms up 2o C.  The soil has a lower specific heat and warms up 10o C, 5 times more than the water (there is a factor of 5 difference in the specific heats of water and soil).

These different rates of warming of water and soil have important effects on regional climate.




Oceans moderate the climate.  Cities near a large body of water won't warm as much in the summer and won't cool as much during the winter compared to a city that is surrounded by land.

The yearly high and low monthly average temperatures are shown at two locations above.  The city on the coast has a 30o F annual range of temperature (range is the difference between the summer and winter temperatures).  The city further inland (assumed to be at the same latitude and altitude) has an annual range of 60o F.  Note that both cities have the same 60o F annual average temperature.

Here's another situation where you can take advantage of water's high specific heat to moderate "micro climate."




This past weekend, I planted a bunch of these tomato plants that had been growing on the window sill in my office. 




Here are a couple of last year's plants.  It can still get cold enough at night this time of year to kill tomatoes (the brocolli and lettuce in the background can handle a light frost).  So you have to protect the tomato plants.




One way of doing that is to put a "wall of water" around each plant.  They take advantage of the high specific heat of water and won't cool as much as the air or soil would during a cold night.

Adding energy to an object will usually cause it to warm.  But there is another possibility (bottom p. 45),  the object could change phase (change from solid to liquid or gas).  Adding energy to ice might cause the ice to melt.  Adding energy to water could cause it to evaporate. 


The equation at the bottom of the figure above allows you to calculate how much energy is required to melt ice or evaporate water or sublimate dry ice.  You multiply the mass by the latent heat, a variable that depends on the particular material that is changing phase. 

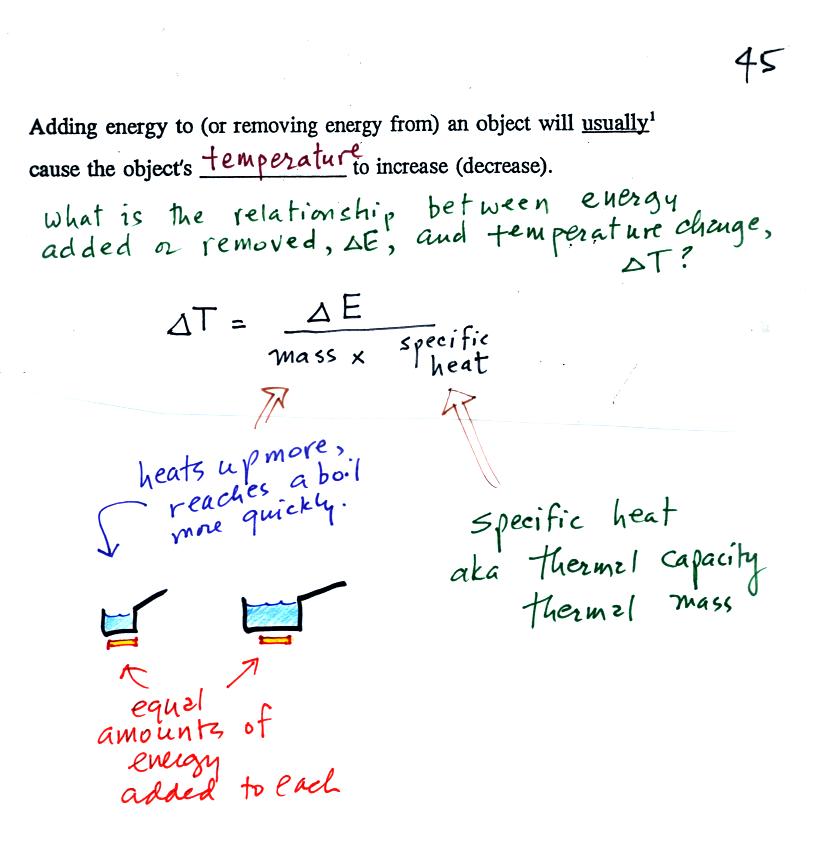
If you add energy to or remove energy from an object, the object will usually change temperature.  You can calculate the temperature change if you know the object's mass and its specific heat.  That's the equation we used in the example calculation earlier.


We will be using the equation next in a slightly different way in a class experiment/demonstration. We will measure the temperature change and use that to determine the amount of energy lost by an object.

Class was interrupted at about this point by a fire alarm.  Most of the students returned afterwards because they had been promised the opportunity to earn a green card.

A couple of students from the class was nice enough to volunteer to perform the experiment (they were both given green cards).

The object of the experiment was to measure the latent heat of vaporization of liquid nitrogen.  That just means measuring the amount of energy needed to evaporate a gram of liquid nitrogen.  The students that are doing Experiment #2 are measuring the latent heat of fusion of ice, the energy needed to melt one gram of ice.  You'll find the following figure on p. 45a in the photocopied Classnotes.



(a)
Some room temperature water poured into a styrofoam cup weighed 120.1 g.  The cup itself weighed 3.3 g, so we had 116.8 g of water.

(b)
The water's temperature was 22.0 C  (room temperature).

(c)
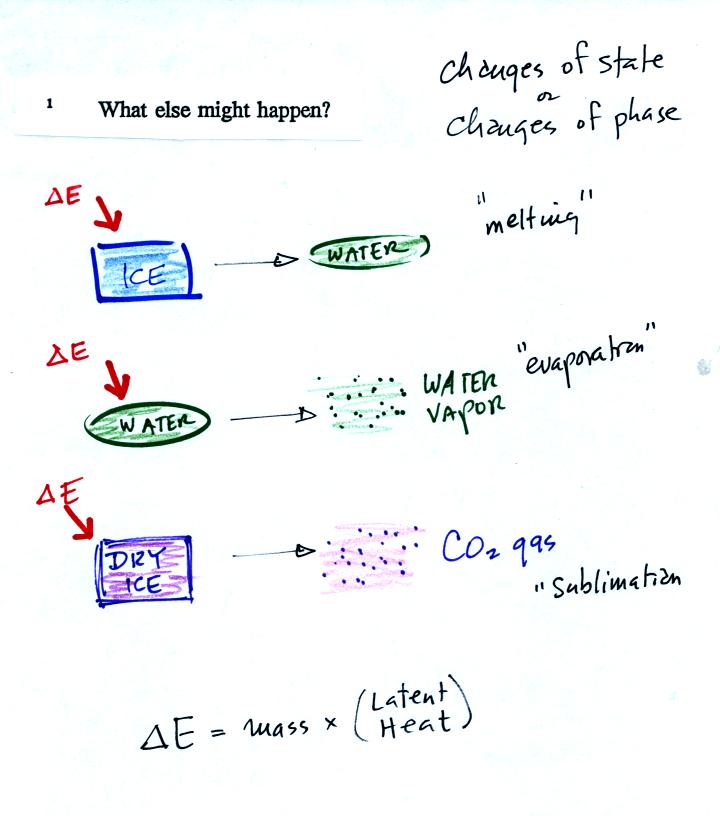
  36.0 g of liquid nitrogen was poured into the cup of water.

It takes energy to turn liquid nitrogen into nitrogen gas.  The needed energy came from the water.  This flow of energy is shown in the middle figure above.  We assumed that because the experiment is performed in a styrofoam cup that there is no energy flowing between the water in the cup and the surounding air.

(d)
After the liquid nitrogen had evaporated we remeasured the water's temperature.  It had dropped to 5.1 C.  That is a temperature drop of 22.0 C - 5.1 C = 16.9 C

Because we knew how much water we started with, its temperature drop, and water's specific heat we can calculate how much energy was taken from the water.

116.8 g. x 16.9 C x 1cal/g C = 1973.9 calories

We then divide that number by the amount of liquid nitrogen that was evaporated.

1973.9 cal / 36.0 g = 54.8 cal/g

A trustworthy student in the class informed us that the known value is 48 cal/g, so our measurement was pretty darn close.

Here's a little more information that we would have covered if it hadn't been for the fire alarm

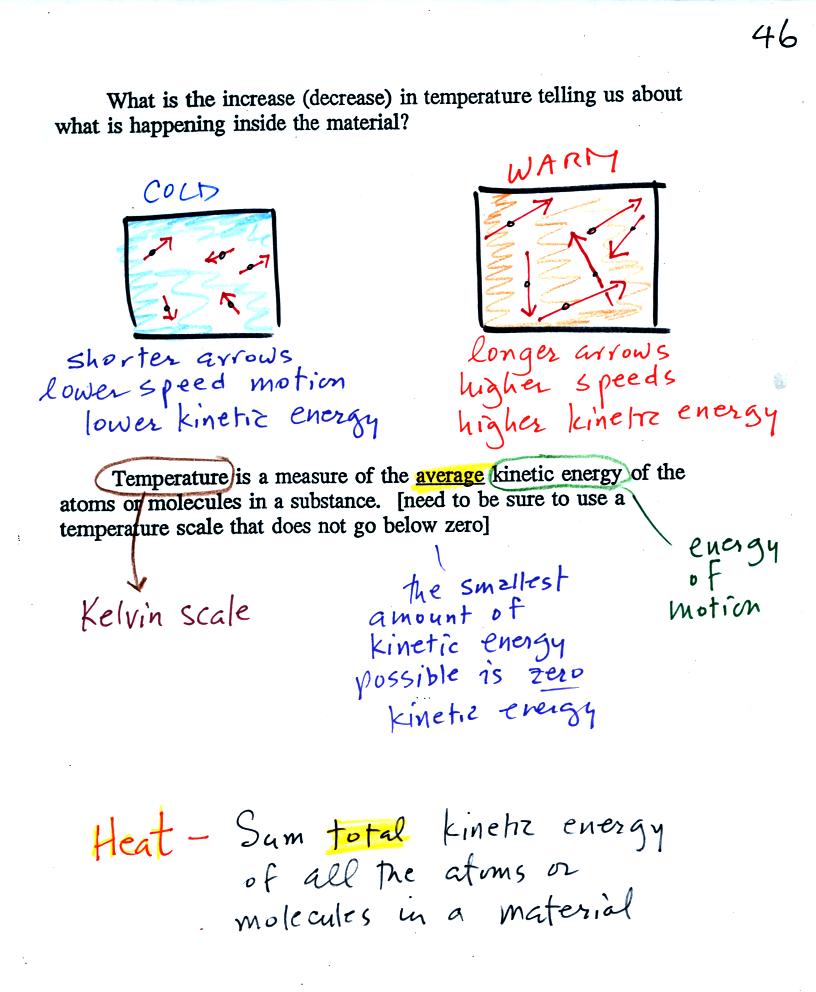
When you add energy to an object and the object warms, what exactly is happening inside the object?

The figure above is on p. 46 in the photocopied Class Notes.  Temperature provides a measure of the average kinetic of the atoms or molecules in a material.  The atoms or molecules in a cold material will be moving more slowly than the atoms or molecules in a warmer object.

You need to be careful what temperature scale you use when using temperature as a measure of average kinetic energy.  You must use the Kelvin temperature scale because it does not go below zero (0 K is known as absolute zero). The smallest kinetic energy you can have is zero kinetic energy.  There is no such thing as negative kinetic energy.

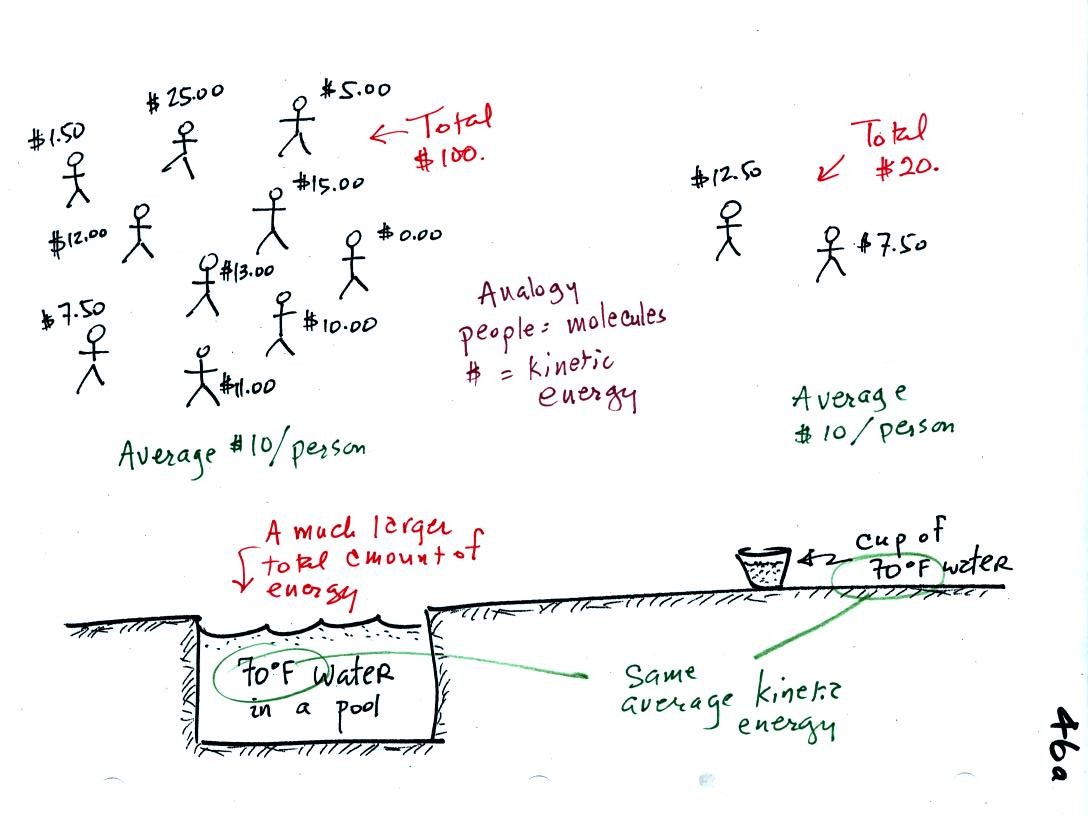
You can think of heat as being the total kinetic energy of all the molecules or atoms in a material.  The next figure might make the distinction between temperature (average kinetic energy) and heat (total kinetic energy) clearer.


A cup of water and a pool of water both have the same temperature.  The average kinetic energy of the water molecules in the pool and in the cup are the same.  There are a lot more molecules in the pool than in the cup.  So if you add together all the kinetic energies of all the molecules in the pool you are going to get a much bigger number than if you sum the kinetic energies of the molecules in the cup.  There is a lot more stored energy in the pool than in the cup.  It would be a lot harder to cool (or warm) all the water in the pool than it would be the cup.

In the same way the two groups of people shown have the same average amount of money per person (that's analogous to temperature).  The $100 held by the larger group at the left is greater than the $20 total possessed by the smaller group of people on the right (total amount of money is analogous to heat). 

Speaking of temperature scales.


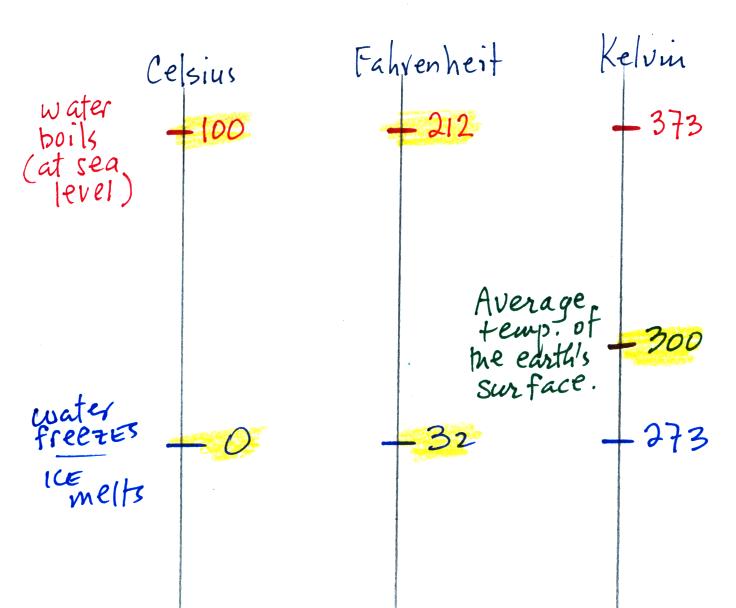
You should remember the temperatures of the boiling point and freezing point of water on the Fahrenheit, Celsius, and perhaps the Kelvin scales.  300 K is a good easy-to-remember value for the global annual average surface temperature of the earth.


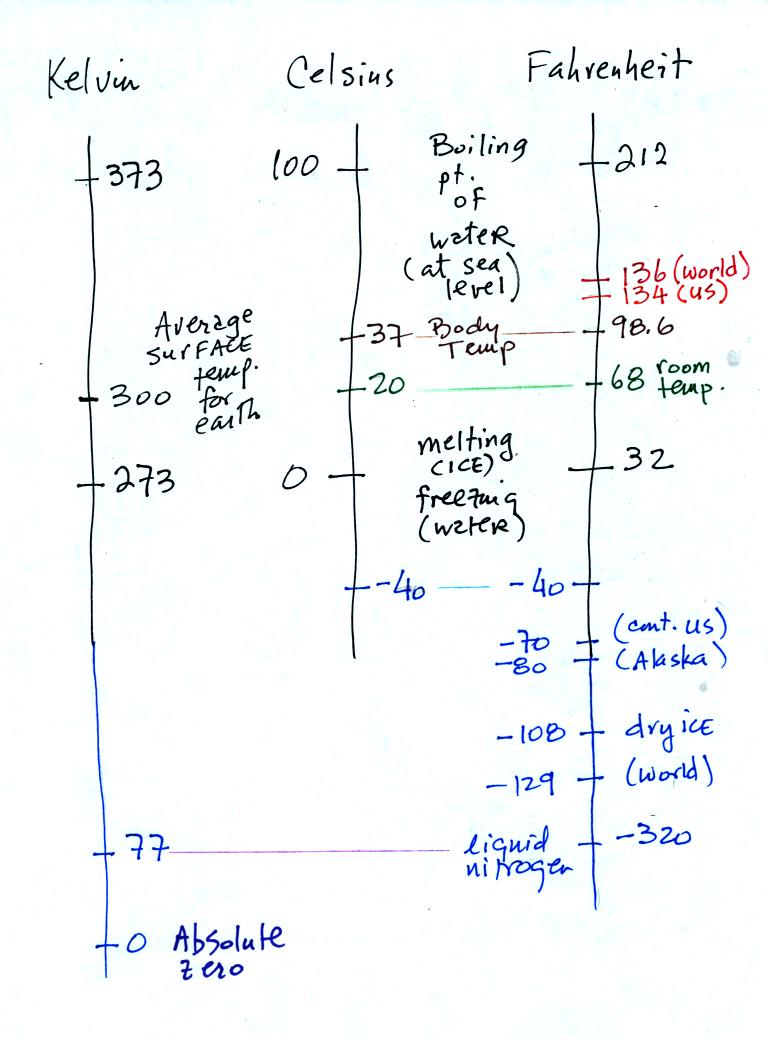
You certainly don't need to try to remember all these numbers.  The world high temperature record was set in Libya, the US record in Death Valley.  The continental US cold temperature record of -70 F was set in Montana and the -80 F value in Alaska.  The world record -129 F was measured at Vostok station in Antarctica.  This unusually cold reading was the result of three factors: high latitude, high altitude, and location in the middle of land rather than being near or surrounded by ocean.     Liquid nitrogen is cold but it is still quite a bit warmer than absolute zero.