
Here's a illustration of the
slitless spectrograph technique that can be used for lightning.
Light from the lightning passes through both a prism and a diffraction
grating and is imaged on film (or a detector of some kind). An
entrance slit is not needed because the lightning source is already a
narrow channel. The spectrum that you would obtain in this case
would be an integration of all the emissions that occurred during the
whole discharge.
To obtain a time resolved spectrum we need to add a horizontal slit to isolate just a segment of the lightning channel and then cause the film to move vertically.

To obtain a time resolved spectrum we need to add a horizontal slit to isolate just a segment of the lightning channel and then cause the film to move vertically.

The film is shown moving downward
in this picture (and sorry that the perspective isn't quite
right). Spectra from two separate return strokes, perhaps, have
been recorded on the film.
The actual arrangements used were shown on a class handout.

The actual arrangements used were shown on a class handout.

The rotating drum in the lower
figure provides the fastest time resolution. Very rapidly
rotating drums in streaking cameras are also used in photographic
measurements of return stroke velocity.
The next figure shows an actual example of a very fast time resolved spectrum from a return stroke.

Here is an example of a "digitized" spectrum. Film's response to light is nonlinear, so the film must be calibrated. Film also reacts different to short bright impulses of light than it does to longer duration low amplitude light signals. So that effect must also be considered.
Six emission lines in the NII(5) multiplet spectrum above have been identified. I am not familiar enough with spectroscopy and quantum mechanics to be able to say for sure what precise states and transitions cause these features

The intensity of the emission produced by transitions from energy level n to r is shown above.
Now we will look at the ratio of measured intensities from two different transitions: n to r and m to p

Note that many of the parameters (that might be difficult to
determine such as the geometric factor) cancel. Solving for
temperature yields

Often what is done is that several determinations of temperature
are made using different combinations of lines in the multiplet group
and an average is computed. In the case of the NII(5) multiplet 5
ratios could be computed: 4630/4601, 4630/4607, 4630/4613, 4630/4621,
and 4630/4643.
The next several figures shown some of the results of these spectroscopic measurements and analyses.

Concentrations of NIII (doubly ionized atomic nitrogen), NII
(singly ionized atomic nitrogen), and NI (neutral atomic nitrogen)
early in a return stroke discharge. NII is initially the most
abundant species and is used in spectroscopic determinations of peak
temperature in the return stroke channel.

Estimate of peak return stroke channel temperature. The
value approaches 30,000 K which is approximately 5 times hotter than
the surface of the sun (6000 K).

Here are estimates of channel pressure. This requires a
measurement of temperature and probably density (including electron
density from the ionized air molecules).
Thunder
Early in a return stroke, pressure in the channel is several times (maybe a few 10s of times) atmospheric pressure. The lightning channel expands rapidly outward initially as a shock wave. Much of the energy in a lightning stroke is dissipated during the formation and outward growth of the shock wave. The shockwave expands outward a few meters in 10s of microseconds and quickly decays into the sound wave that we eventually hear as thunder.
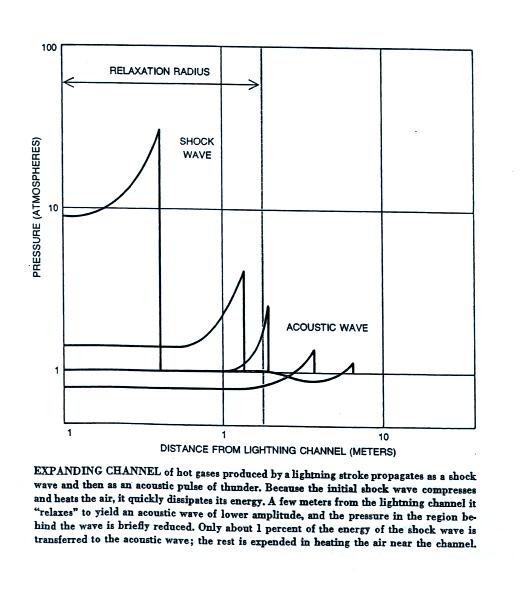
This figure (this and the next two figures are from an article on
Thunder by A.A. Few that appeared in "The Physics of Everyday
Phenomena", Readings from Scientific American, W.H. Freeman & Co,
San Francisco, 1979) shows the transition from shock wave to sound
wave. The size of the channel whens this occurs is referred to as
the relaxation radius. Small scale channel tortuosity features
are swallowed up by the shock wave and don't really affect properties
of the thunder such as frequency.

Lightning channels consist first of mesotortuous segments that are
5 to a few 10s of meters long. Several of these positioned
end-to-end and oriented in about the same direction form a
macrotortuous segment. The variation of sounds that are heard
during thunder are determined primarily by your orientation relative to
the mesotortuous elements. Sounds emitted in a direction that
perpendicular to the channel are louder than sounds emitted more nearly
parallel to the channel.
Four relatively loud sound pulses arrive in quick succession at the first microphone and form a clap of clap of thunder. Weaker impulses arrive at the second microphone over a longer period of time and produce more of a rumple.
It is generally not possible to separate the sounds of the separate return strokes in a thunder record (either by ear or on thunder recordings).
I mentioned in class a sound that resembles "tearing cloth" that precedes the loud clap of thunder from a close lightning strike. Most students seemed to agree that they had heard something like this. The cause of that sound is not known.
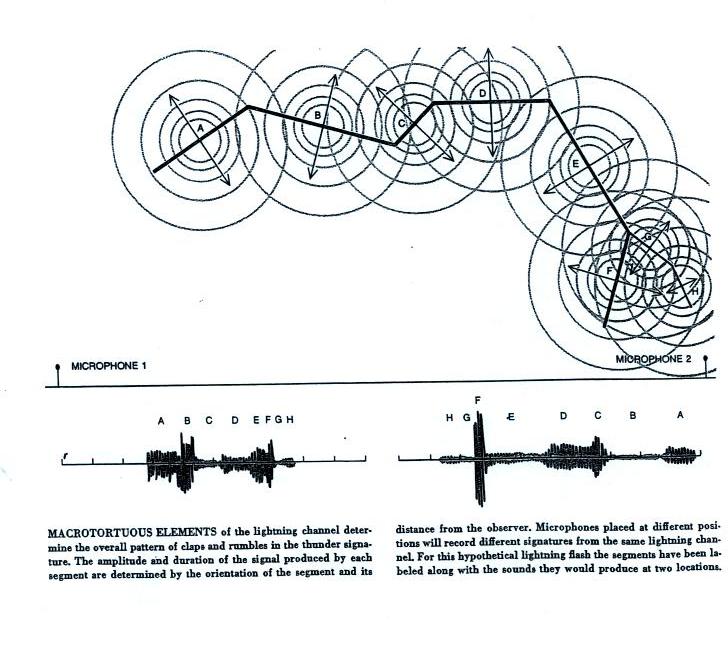
Another illustration of how the pattern of sounds in thunder and the duration of the thunder depend on your location and the structure of the lightning channel.
The duration of thunder is explored a little more in the next figure.

The next figure shows an actual example of a very fast time resolved spectrum from a return stroke.

Several emission features are
identified on this spectrum early in the return stroke discharge (NII
is a singly ionized nitrogen atom). Now what is usually done next
is to scan across the film image using a densitometer at say perhaps
the level of the green line (i.e. at a time about 10 microseconds after
the beginning of the return stroke).


Here is an example of a "digitized" spectrum. Film's response to light is nonlinear, so the film must be calibrated. Film also reacts different to short bright impulses of light than it does to longer duration low amplitude light signals. So that effect must also be considered.
Six emission lines in the NII(5) multiplet spectrum above have been identified. I am not familiar enough with spectroscopy and quantum mechanics to be able to say for sure what precise states and transitions cause these features

but I'm guessing it looks something
like shown here. Transitions from 2 slightly different energy
levels from an excited state to 1 of 3 levels at a lower energy state
could produce emissions of 6 slightly different wavelengths.
In any event it is the relative amplitudes of lines in a multiplet group that can be used to estimate lightning channel temperature. The procedure is described below. Our goal is not understand all the steps but rather to get a flavor for the procedure or method.
The first assumption made is that the number of atoms in a particular energy level can be described using a Maxwell-Boltzmann distribution

Nn is the number of atoms in energy level n, N is the total number of atoms.

In any event it is the relative amplitudes of lines in a multiplet group that can be used to estimate lightning channel temperature. The procedure is described below. Our goal is not understand all the steps but rather to get a flavor for the procedure or method.
The first assumption made is that the number of atoms in a particular energy level can be described using a Maxwell-Boltzmann distribution

Nn is the number of atoms in energy level n, N is the total number of atoms.

The intensity of the emission produced by transitions from energy level n to r is shown above.
Now we will look at the ratio of measured intensities from two different transitions: n to r and m to p


The next several figures shown some of the results of these spectroscopic measurements and analyses.



Thunder
Early in a return stroke, pressure in the channel is several times (maybe a few 10s of times) atmospheric pressure. The lightning channel expands rapidly outward initially as a shock wave. Much of the energy in a lightning stroke is dissipated during the formation and outward growth of the shock wave. The shockwave expands outward a few meters in 10s of microseconds and quickly decays into the sound wave that we eventually hear as thunder.


Four relatively loud sound pulses arrive in quick succession at the first microphone and form a clap of clap of thunder. Weaker impulses arrive at the second microphone over a longer period of time and produce more of a rumple.
It is generally not possible to separate the sounds of the separate return strokes in a thunder record (either by ear or on thunder recordings).
I mentioned in class a sound that resembles "tearing cloth" that precedes the loud clap of thunder from a close lightning strike. Most students seemed to agree that they had heard something like this. The cause of that sound is not known.

Another illustration of how the pattern of sounds in thunder and the duration of the thunder depend on your location and the structure of the lightning channel.
The duration of thunder is explored a little more in the next figure.

Measurements of thunder duration
for discharges at different distances (points). The solid line is
a calculation of thunder duration from a vertical lightning channel 7
km tall. A and B refer to the calculations below.

Person A in the figure above will hear the thunder coming from the
bottom of the channel instantaneously. Sound travels about 340
m/sec in 20 C air (1 km in 3 seconds, 1 mile in approximately 5
seconds), so the sound from the top of the channel will arrive about 21
seconds later. That's a duration of 21 seconds.
The observer at Point B will hear the thunder from the bottom of the channel 30 seconds after the lightning strike. Thunder coming from the top of the channel will arrive about 6.6 seconds later (3 seconds/km x 2.2 km). The thunder only lasts for about 6.5 seconds at Point B.
Wind can affect the sound of thunder and refraction can mean there is a distance beyond which thunder is not heard.



The observer at Point B will hear the thunder from the bottom of the channel 30 seconds after the lightning strike. Thunder coming from the top of the channel will arrive about 6.6 seconds later (3 seconds/km x 2.2 km). The thunder only lasts for about 6.5 seconds at Point B.
Wind can affect the sound of thunder and refraction can mean there is a distance beyond which thunder is not heard.

Here are a couple of plots of the
frequency spectrum of lightning

The first plot is actually a
distribution of peak values in sound spectra. Interestingly the
peak in the thunder sound spectrum is below 20 Hz and is inaudible
(this is infrasound).
I
showed
the
response
curve for a microphone that has been used to
record thunder. The response was flat from 0.5 Hz up to about 200
or 300 Hz.


An example of a sound spectrum
(lower right corner) that peaks in the infrasound. At upper right
the arrival times of the different frequencies in thunder.
Infrasound is the earliest arrival in the figure and contnues
throughout the discharge.
Ground-based Optical Measurements of Lightning
Now the last topic of the day. We'll use a paper by C. Guo and E.P. Krider ("The Optical and Radiation Field Signatures Produced by Lightning Return Strokes," J. Geophys. Res., 87, 8913-8922, 1982) as an example of what can be learned about lightning optical emissions using a fairly straightforward ground based sensor.

Ground-based Optical Measurements of Lightning
Now the last topic of the day. We'll use a paper by C. Guo and E.P. Krider ("The Optical and Radiation Field Signatures Produced by Lightning Return Strokes," J. Geophys. Res., 87, 8913-8922, 1982) as an example of what can be learned about lightning optical emissions using a fairly straightforward ground based sensor.

This first figure shows the sensor
(a photodiode) and its elevation angle response. The system would
see the entire lightning channel between the ground and cloud base
unless the lightning was close to the observing location.


Wavelength response for the
photodiodes used in the experiment.

Examples of recorded electric fields (E, shaded blue) and associated optical signals (O, highlighted in yellow). This was a four stroke cloud-to-ground discharge that occurred at 13 km range. The first return stroke is shown at the bottom of the figure. These waveforms were photographed on moving film. The dark black timing marks were from an LED that would flash on and off to code the absolute time onto the film.


Examples of recorded electric fields (E, shaded blue) and associated optical signals (O, highlighted in yellow). This was a four stroke cloud-to-ground discharge that occurred at 13 km range. The first return stroke is shown at the bottom of the figure. These waveforms were photographed on moving film. The dark black timing marks were from an LED that would flash on and off to code the absolute time onto the film.

We can use a measurement of the
peak optical signal amplitude, a measurement of peak irradiance, to
estimate the peak optical power output from a lightning return stroke.


We treat the lightning discharge as
a point source. The peak optical power output during the strike
will expand evenly outward into a sphere. We measure the peak
irradiance, Lp, a distance D from the source. So to estimate P we
simply multiply the measured values of Lp by the area of the sphere.

Here's a cumulative distribution of peak optical power
estimates. 50% of 1st return strokes have a peak optical power
output of about 2 x 109 Watts or
more. Peak power emitted by
subsequent strokes is almost a factor of 10 less.
We'll come back to this topic briefly at the start of class next Tuesday.

We'll come back to this topic briefly at the start of class next Tuesday.