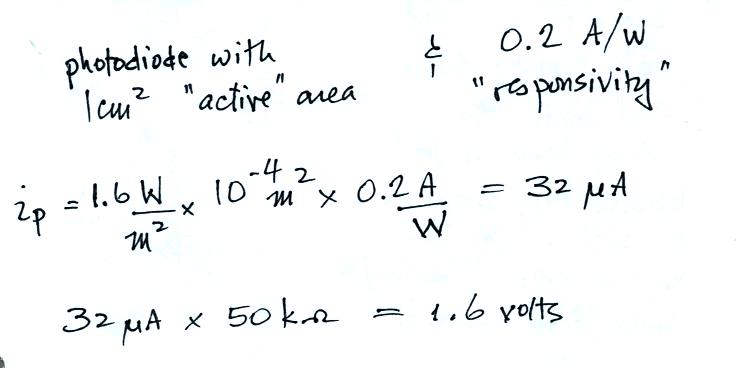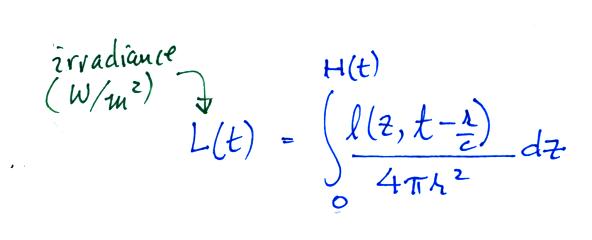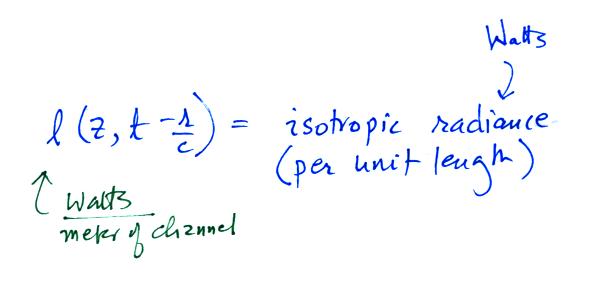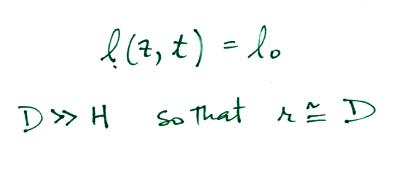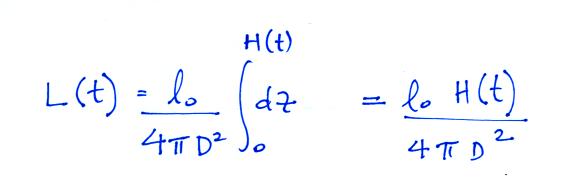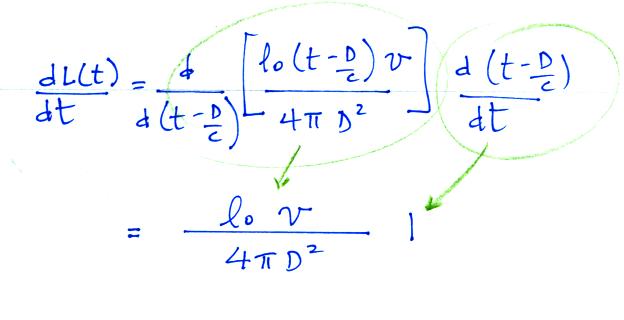Tuesday Apr. 26, 2011
click here to
download today's notes in a more printer friendly format
We began by finishing the section on ground based optical
measurements of lightning.
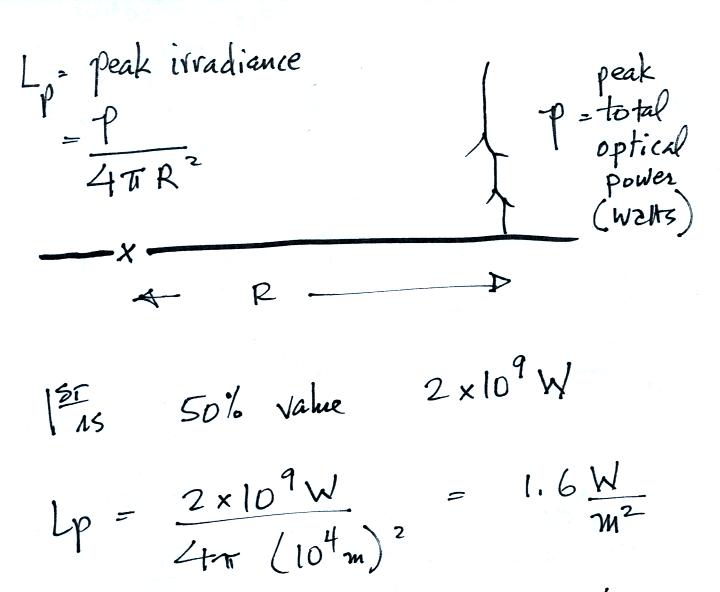
In the last class we saw how a measurement of Lp, the peak
irradiance, measured a distance R from a return stroke could be used to
determine the peak total optical power emitted by the return stroke (we
treated the return stroke as a point source and assumed that the light
signals were emitted uniformly in all directions).
Today we will look at a simple sensor system that could be used to
measure Lp. We start, above, by assuming a reasonable value for P
and calculating the Lp we would expect to see at a distance of 10 km.
The light emitted by lightning is relatively bright and a simple
photodiode can be used to detect lightning optical signals. An
example photodiode was brought to class.
The photodiode had an active (sensing) area of 1 cm2
and a
responsivity of 0.2 A/W. The diode can not produce a current
anywheres near 0.2 Amps. It is designed to detect signals of much
less than 1 Watt. In the example above, for example, it collects
1.6 x 10-4 W and is able to produce an output current of 32
microamps. A current this small is easily converted to a
measureable voltage using one of the op-amp (operational amplifier)
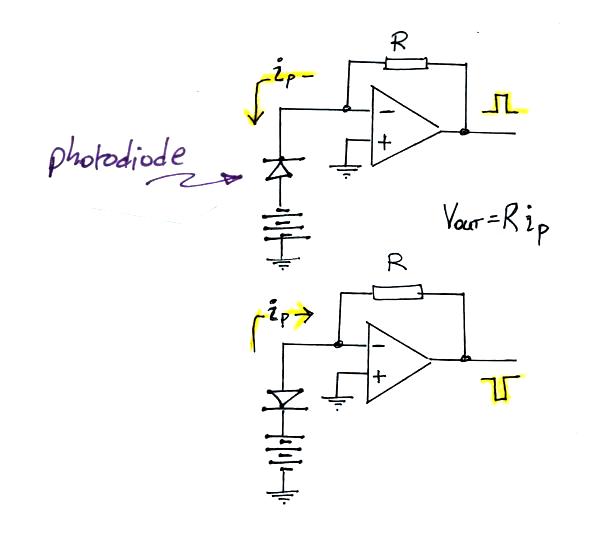
circuits below.
The two circuits are essentially identical except for the
orientation of the photodiode. The orientation in the top figure
gives a positive-going output signal. The bottom circuit produces
a negative polarity output.
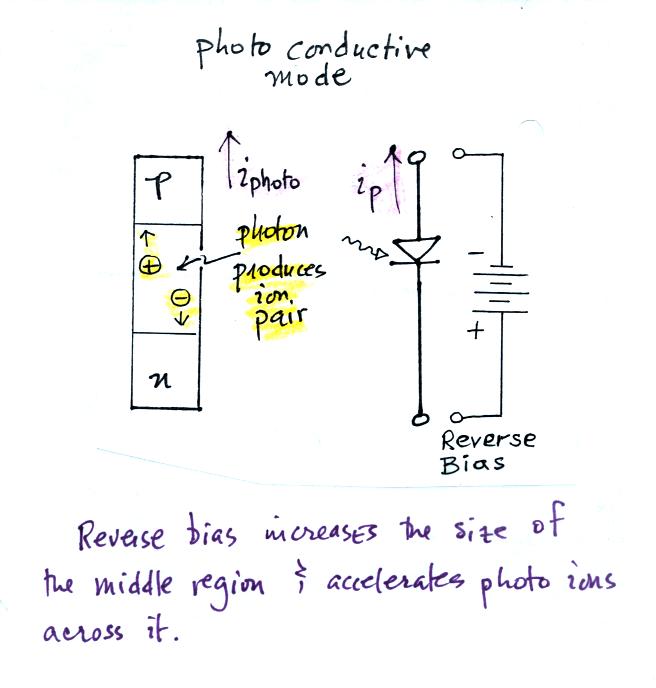
The photodiodes in the circuit above are being operated in the
photoconductive mode (diode produces a current that is proportional to
the intensity of the incident light signal) and are back biased.
This explained further in the next few figures.
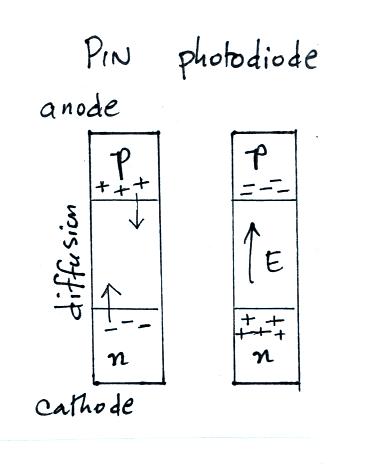
A PIN photodiode (and this is my very incomplete understanding of
them) consists of a "p-doped" region, an intrinsic (undoped) region,
and an "n-doped" region. The term "doping" means impurities have
been added to a semiconductor material such as silicon. An
n-doping material (such as phosphorus) effectively adds negative
polarity charge carriers, the p-doping material (boron or aluminum?)
positive charge carriers. Charge diffuses from the doped regions
across the intrinsic region in the middle. Movement of the charge
carriers creates an electric field which, once it grows to sufficient
strength, limits the amount of charge buildup.
Photons which strike the intrinsic region of the photodiode
produce photoions. Back biasing the photodiode increases the
response speed of the photodiode.
Back to optical measurements of lightning after that digression.
So far we have used the peak optical signal amplitude to estimate the
peak optical power emitted by return strokes. Next we will
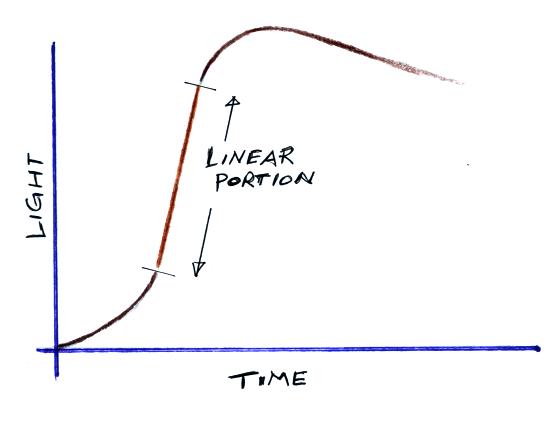
consider the linear portion of the rising front on a lightning optical
waveform.
We will assume that this is produced by the geometric growth of
the return stroke channel as it propagates from the ground up toward
the bottom of the cloud (the signal amplitude grows as the channel gets
taller). We'll also assume the channel is straight and vertical
and that the return stroke velocity is constant.
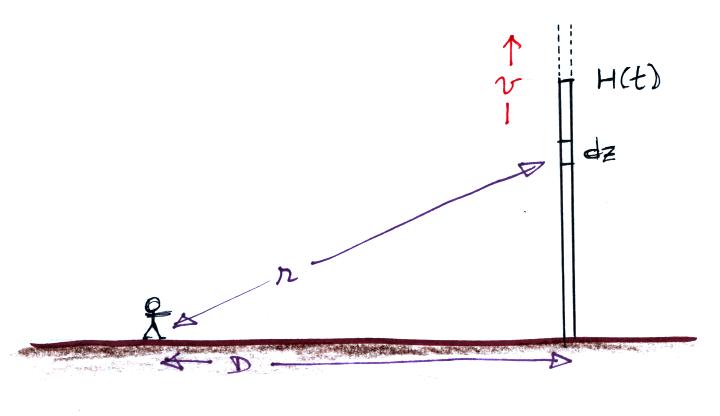
Optical emissions from the along the length of the channel between the
ground and H(t) determine the amplitude of the signal at time t.
The equation is pretty general at this point, we allow l(z,t) to
vary with z and t.
We'll make a couple of simplifying assumptions
Then the integral becomes
we'll replace H(t) with a time multiplied by velocity term
Here you can clearly see that L(t), measured at distance D would
increase linearly with time.
Next we differentiate this expression
dL(t)/dt is just the slope of the linear portion of the optical
signal waveform. We assume the distance to the discharge is known
and assume a value for the return stroke velocity. This provides
us with an estimate of the mean radiance per unit length for a return
stroke discharge.
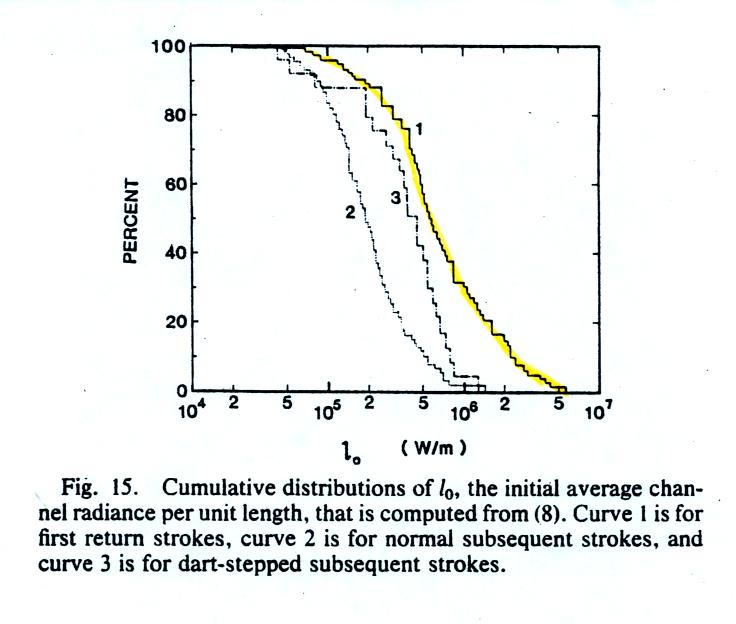
Actual measurements of mean radiance per unit length. A
return stroke velocity of 8 x 107 m/s was assumed. Discharges
were 5 to 35 km from the measuring site.
Because I
haven't managed to get the notes on sprites, elves, and blue jets
online yet, there won't be any questions about this material on the
Final Exam.
sprite
pictures (sky-fire.tv) (also blue jets and elves)
sprite movie
(Univ. AK, Geophys. Inst.)
sprite research
(NM Tech)
sprite movie
high
speed video (NM Tech)
sprite movie high
speed video (NM Tech)
blue jet movie
(Univ. AK, Geophys. Inst.)
whistlers
(audio)
whistlers
(spectogram)