
Coulomb's law tells you the force
that q1 will exert on q2. If q1 and q2 both have the same
polarity q2 will be repelled by q1. If they have opposite
charges, q2 will be attracted to q1. It is an inverse square
law. Note the vector and unit vector notations that will be used
in this class. We'll also mostly be using mks units.


The principle of superposition
applies: when multiple charges are present, the force exerted on one of
the charges is the vector sum of the forces exerted on the charge by
all the other charges.

We will mostly be using the MKS system of units
in this class. I'd encourage you to put all the constants and
units together on one page so that you can refer to for homework and
exam questions.
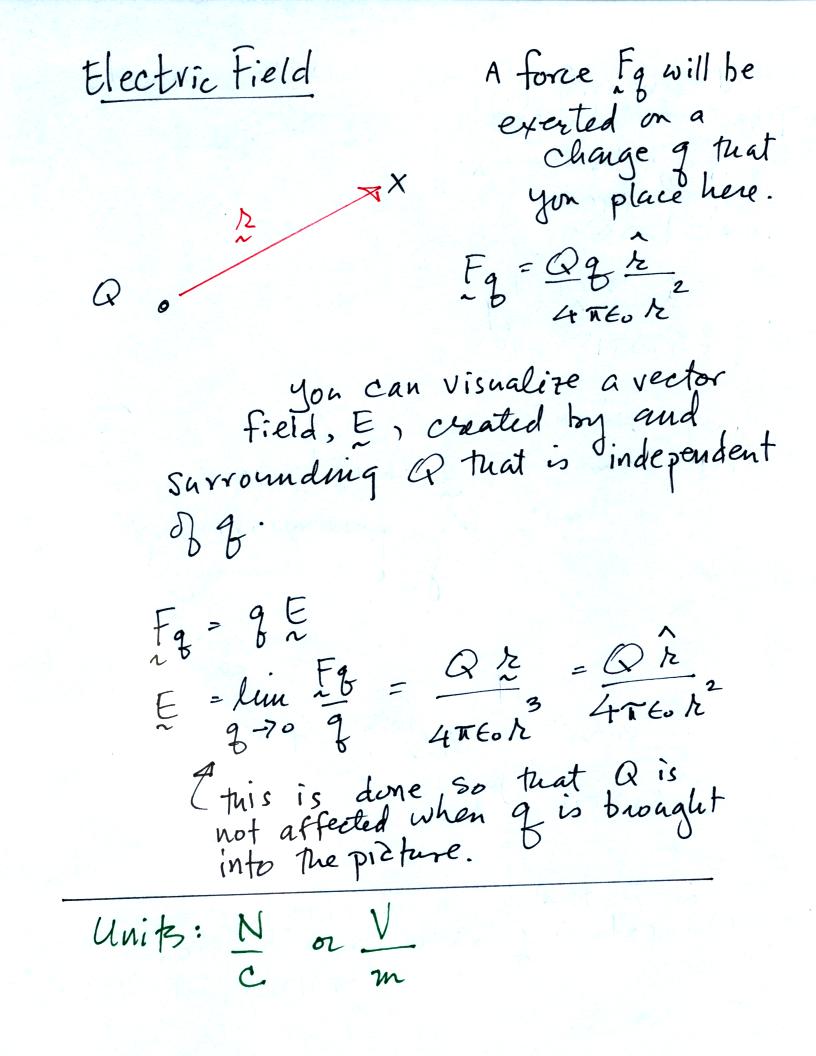
If a charge q is placed in the
vicinity of a charge Q, we could use Coulomb's law to determine the
force that Q exerts on q. We can imagine a vector field, the
electric field, existing around Q even before q is brought into the
picture. Multiplying q times E would give the force that Q exerts
on q. The expression for electric field is shown above.
We'll try an example problem: calculating the field a distance r away from an infinitely long line of charge.
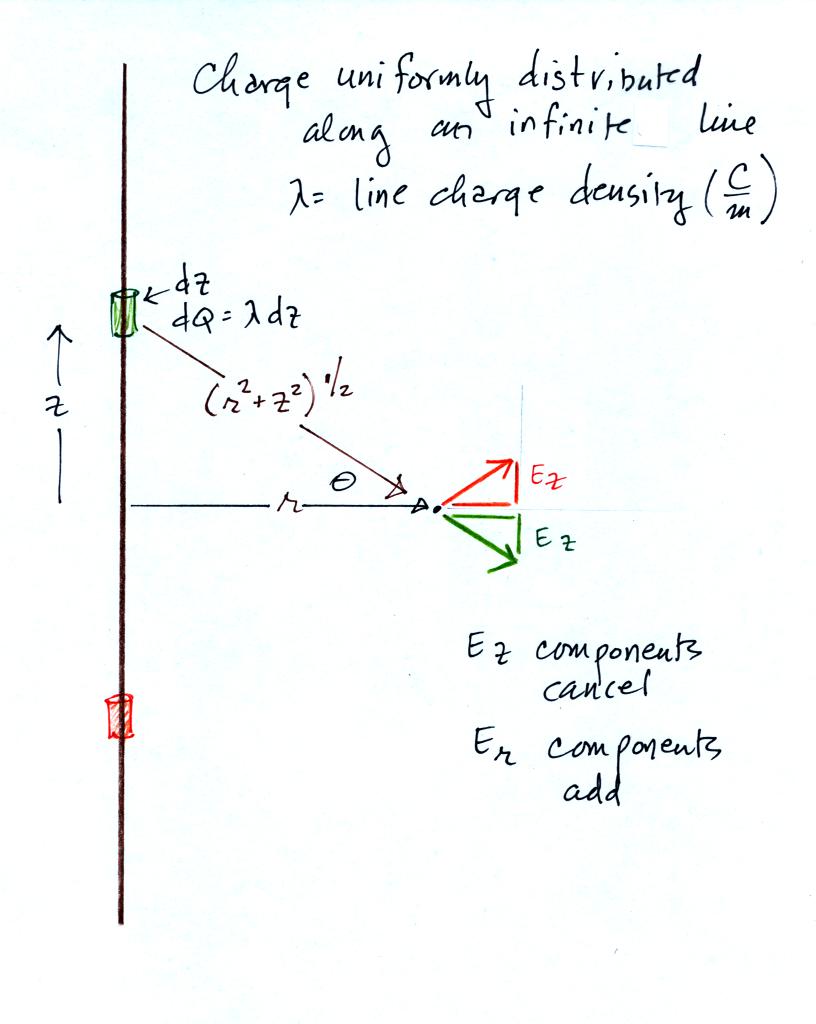
Short segments above and below z=0 contribute to the field. The z components cancel, the r components add.



We'll try an example problem: calculating the field a distance r away from an infinitely long line of charge.

Short segments above and below z=0 contribute to the field. The z components cancel, the r components add.

We'll come back to this problem and
solve it in a much simpler way.
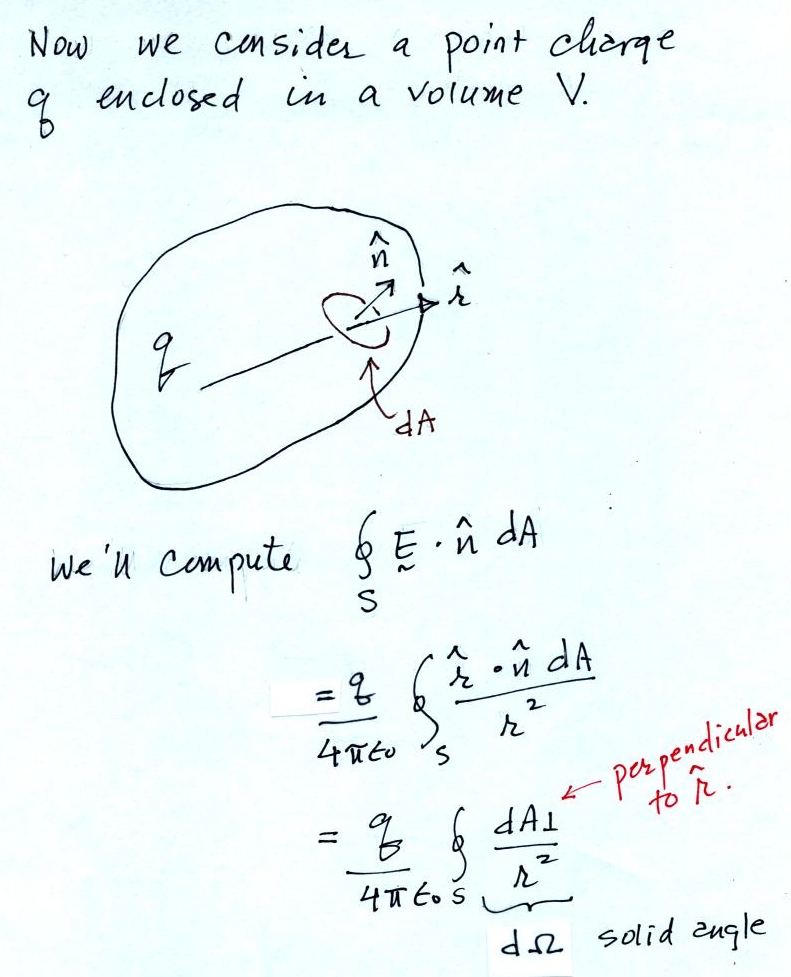

This is the integral form of Gauss' Law.
We'll return to our earlier problem and use Gauss' Law to determine the electric field. We'll see that it is a much easier process.
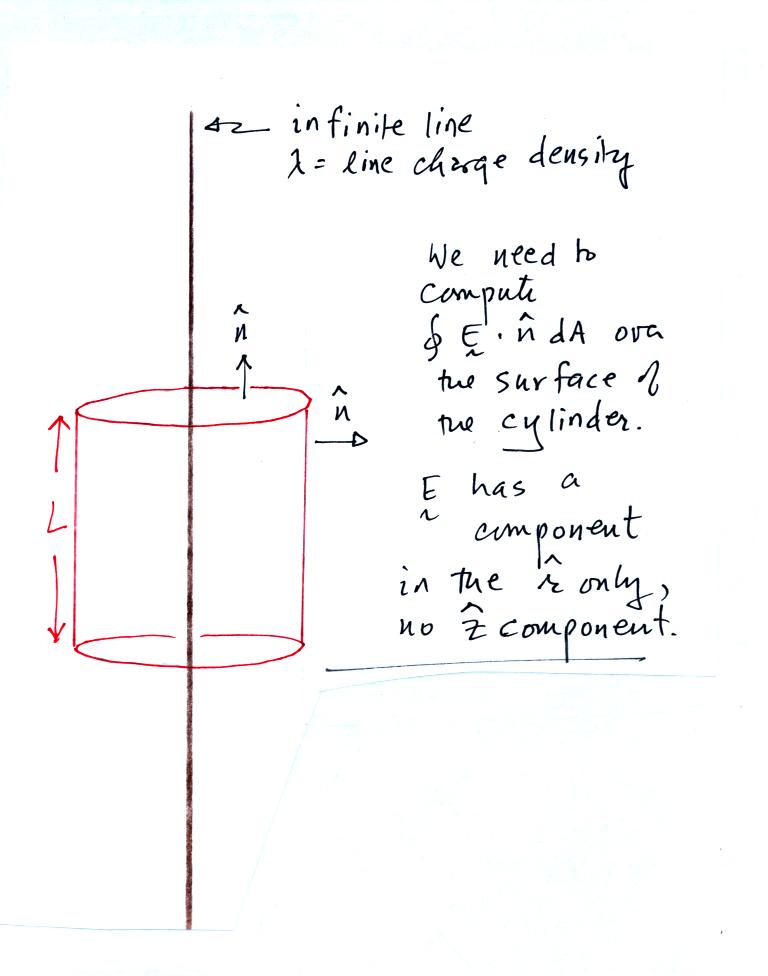
We draw a cylinder around the line of charge. This is the
area that we will integrate E over in the Gauss Law expression.
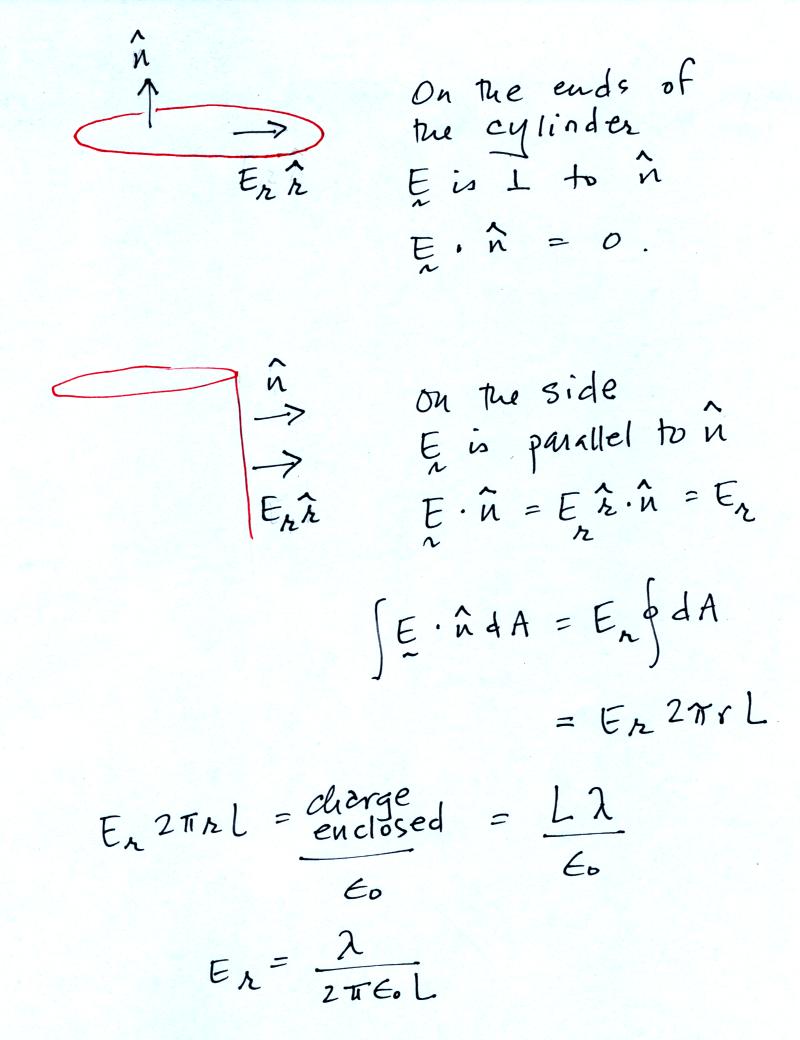
There is no contribution to the integral from the ends of the
cylinder (E is perpendicular to the normal vector, the dot product is
zero). E is parallel to the normal vector along the side of the
cylinder. E is also constant on the side of the cyliner (E is a
function of r and r stays constant as you integrate over the surface of
the cylinder side). In the end we obtain the same expression for
E as we did in the earlier example.
It's relatively easy to show that the surface integral of the E is zero when charge is located outside the volume. This wasn't done in class.

Along the front portion of the surface the r unit vector points inward, n points outward. Along the back surface r and n both point outward. The two increments of solid angle have the same value but opposite signs so they cancel.
We can use the divergence theorem to write the surface integral of E as a volume integral of the divergence of E.
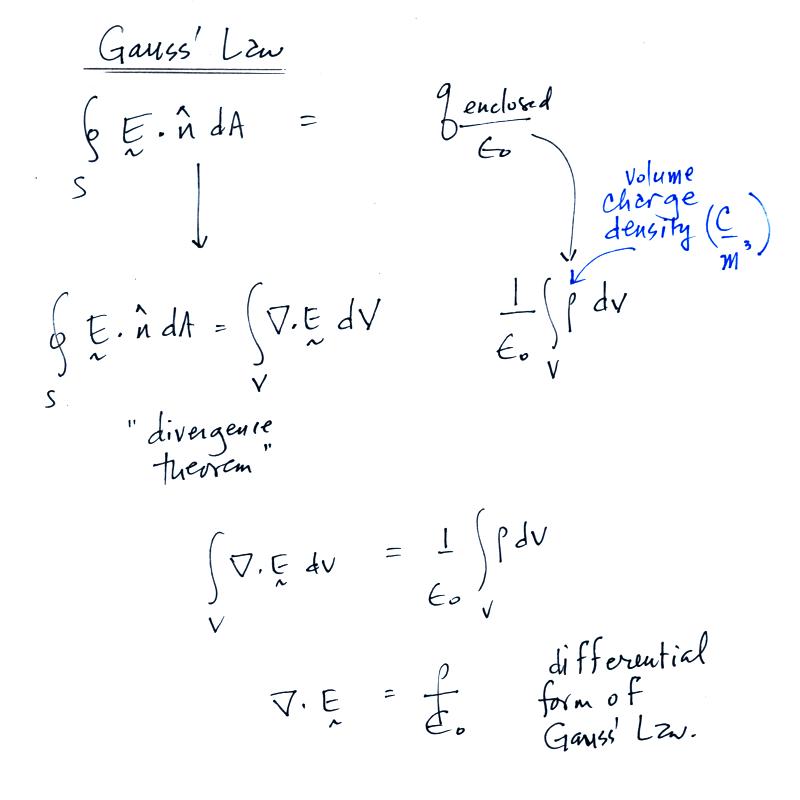
The charge enclosed by a volume of space charge is the volume integral of the space charge density rho. We can set the two volume integrals equal to each other and obtain the differential form of Gauss' law.
We're almost done for today.
Next we imagine placing a conductor in an electric field

Free electrons inside the conductor will quickly move around and redistribute themselves in such a way that they will cancel out the field in the conductor (as the electrons move they leave behind positively charged atoms). Very quickly the field inside the conductor will become zero. There is also no space charge inside the conductor, all the charge is distributed along the surface on the conductor. The electric field lines in the vicinity of the conductor will be distorted and will strike the surface of the conductor perpendicular (if there were any tangential component, charges would move and cancel it out).
Next we'll use Gauss' Law to determine a relationship between the surface charge density and the electric field strength at the surface of a conductor.
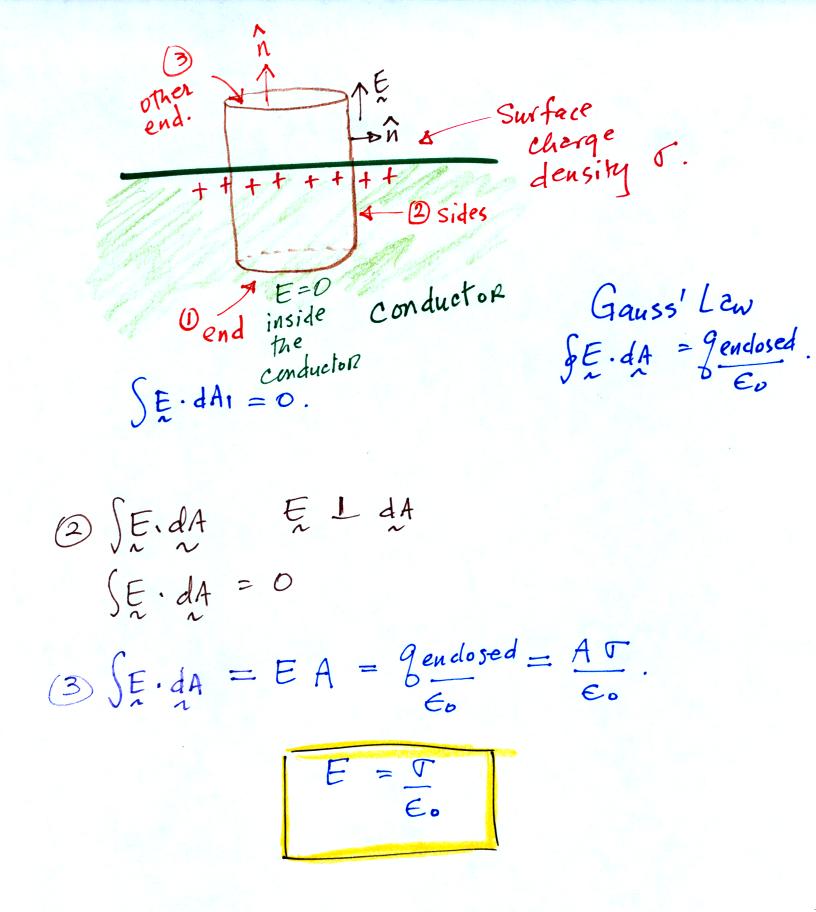
A cylindrical volume, half inside and half outside the conductor
is
used. You must integrate the electric field, E, over the surface
of the cylinder.
1. The E field is zero inside the conductor. So you get no contribution to the surface integral from the bottom end of the cylinder.
2. Along the sides of the cylinder, E is perpendicular to the vector normal to the surface. So there is no contribution to the surface integral from the sides of the cylinder.
3. The only contribution comes from the top end of the cylinder. E and the normal vector are parallel. So the contribution from the top end is just E A, where A is the area of the top end of the cylinder. The charge enclosed is just A σ, where σ is the surface charge density. The electric field at the surface of the conductor is perpendicular to the conductor and has the value highlighted in yellow.


We'll return to our earlier problem and use Gauss' Law to determine the electric field. We'll see that it is a much easier process.


It's relatively easy to show that the surface integral of the E is zero when charge is located outside the volume. This wasn't done in class.

Along the front portion of the surface the r unit vector points inward, n points outward. Along the back surface r and n both point outward. The two increments of solid angle have the same value but opposite signs so they cancel.
We can use the divergence theorem to write the surface integral of E as a volume integral of the divergence of E.

The charge enclosed by a volume of space charge is the volume integral of the space charge density rho. We can set the two volume integrals equal to each other and obtain the differential form of Gauss' law.
We're almost done for today.
Next we imagine placing a conductor in an electric field

Free electrons inside the conductor will quickly move around and redistribute themselves in such a way that they will cancel out the field in the conductor (as the electrons move they leave behind positively charged atoms). Very quickly the field inside the conductor will become zero. There is also no space charge inside the conductor, all the charge is distributed along the surface on the conductor. The electric field lines in the vicinity of the conductor will be distorted and will strike the surface of the conductor perpendicular (if there were any tangential component, charges would move and cancel it out).
Next we'll use Gauss' Law to determine a relationship between the surface charge density and the electric field strength at the surface of a conductor.

1. The E field is zero inside the conductor. So you get no contribution to the surface integral from the bottom end of the cylinder.
2. Along the sides of the cylinder, E is perpendicular to the vector normal to the surface. So there is no contribution to the surface integral from the sides of the cylinder.
3. The only contribution comes from the top end of the cylinder. E and the normal vector are parallel. So the contribution from the top end is just E A, where A is the area of the top end of the cylinder. The charge enclosed is just A σ, where σ is the surface charge density. The electric field at the surface of the conductor is perpendicular to the conductor and has the value highlighted in yellow.