Thursday Jan. 27, 2011
click here to download today's notes in a more printer friendly format.

We finished up the discussion of flat plate electric field antennas that we started on Tuesday.

Here's the passive integrator circuit that we ended up with last Tuesday.  A 10 V/m is typical of what you might expect from a natural 1st return stroke discharge in a cloud-to-ground flash at 100 km range.  A 20 pF capacitor was needed to give a 1 volt output signal.  20 pF in parallel with a 1 megohm resistor would give a decay time constant of 20 usec.  A return stroke might last 100 to 200 usec, so this is too short.

There are situations where a passive integrator circuit might be suitable.

A triggered lightning discharge at 100 meters range will produce a much larger E field change signal.  You could make the integrating capacitor larger (with a corresponding longer decay time constant).  Actually you would probably also need to reduce the area of the antenna plate so as to not have too large an output signal.  In the case of triggered lightning, signals from antennas and other sensors are generally carried into a shielded metal trailer on fiber optics cables for safety reasons.

It is more common to connect the flat plate antenna to an active integrator circuit as shown below


When the E field antenna sensor plate is connected to an active integrator circuit like shown above, the input impedance of the measuring equipment won't affect the decay time constant.  The decay time constant is determined by the R and C values in the operational amplifier feedback circuit.

Next a couple of figures to try to make clear the differences between "fast E" and "slow E" antenna systems.


A slow E field antenna is used to faithfully reproduce field changes from an entire discharge.  Not just return stroke changes but also leader processes and continuing currents that might occur between return strokes.  Since a typical discharge lasts 0.5 to 1 second, the decay time constant must be several seconds long.   The field changes superimpose on each other and the gain must be adjusted to keep the entire signal onscale.

Charged precipitation will sometimes carry enough charge to the antenna plate to drive a slow E field signal off scale.  One solution is to invert the antenna just as is sometimes done with field mills.


Fast E field antennas are used to examine portions of the discharge on a faster time scale.  You might record and display the fields produced by the return strokes on a microsecond time scale for example.

A shorter decay time constant is used so that the output signal can return to zero in between separate discharges.  The gain can be increased because you only need to keep signals from individual strokes rather than the entire discharge onscale.  A system with a fast decay time is affected less by charged rain.

Here are typical Fast E and Slow E integrator circuits.  In particular a way of getting the long decay time constants used in slow E field antenna systems.

Next a couple of comments about the homework assignment.

First rho was a bad symbol choice for line charge density in Problem #2.  Use lambda for line charge density and rho for volume charge density.


There is just one additional problem, a charge Q positioned above a flat infinite grounded conducting plane.  The best way to handle a problem like this is to use the method of images.  A charge Q and a charge -Q placed a distance 2H apart will recreate the boundary condition of zero potential on a flat infinite surface midway between the two charges. 

The best way to handle Problem #3 is to use the method of images.  A charge Q and a charge -Q placed a distance 2H apart will recreate the boundary condition of zero potential on a flat infinite surface midway between the two charges.



This is an important problem.  We'll have occasion to use the results several times later in the semester.


Once you've worked out the problem with one charge, it's easy to add a second charge (at a different altitude above the ground).


And rather than thinking about E fields produced by charges in a thunderstorm, you can think about E field changes produced when a certain amount of charge in the cloud is neutralized.

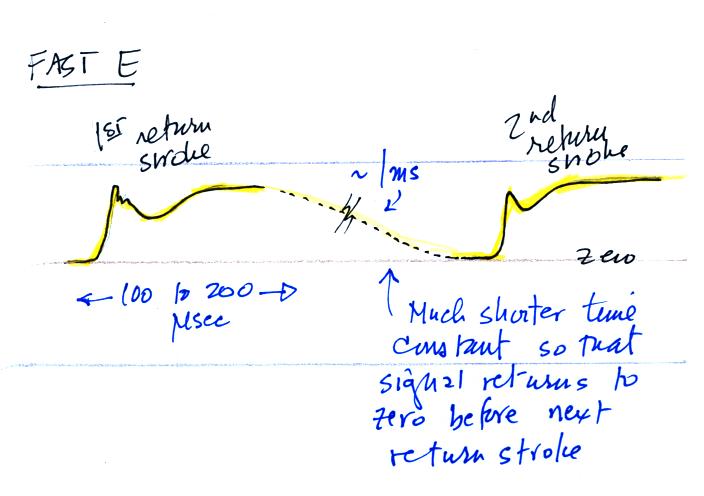
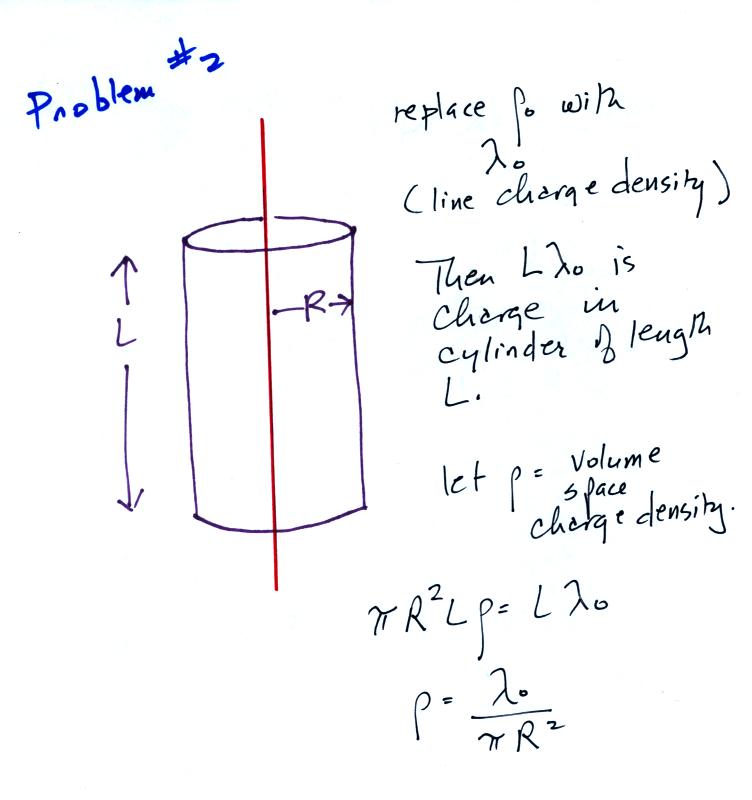
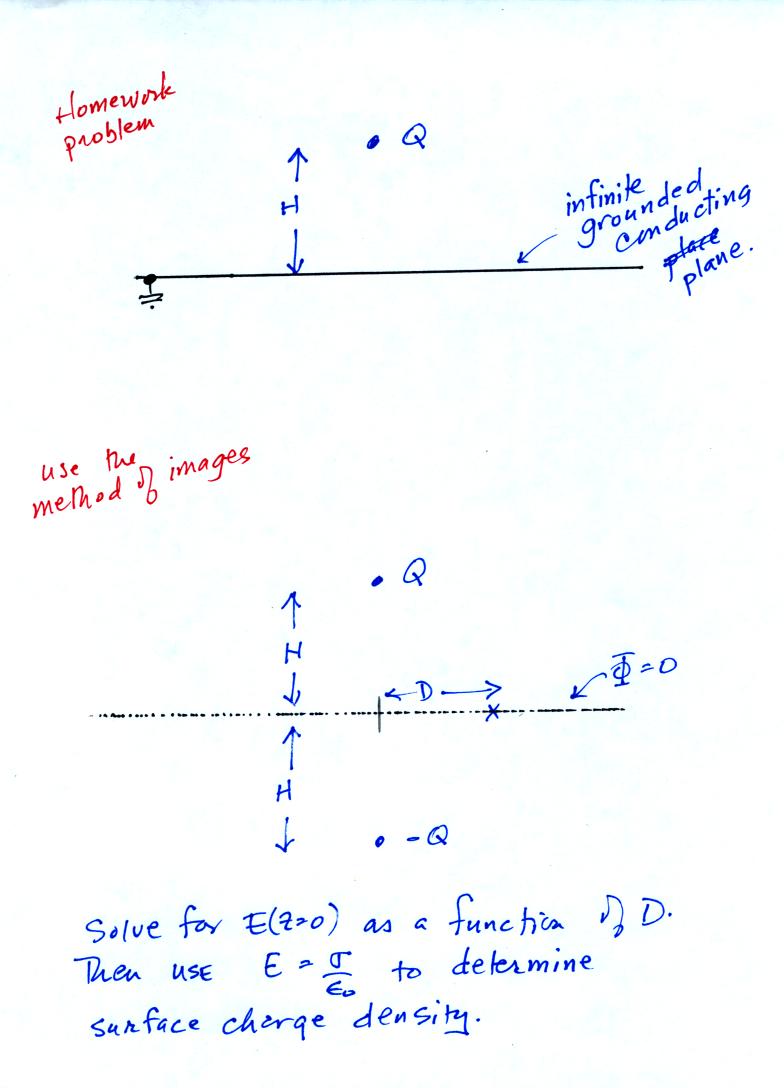
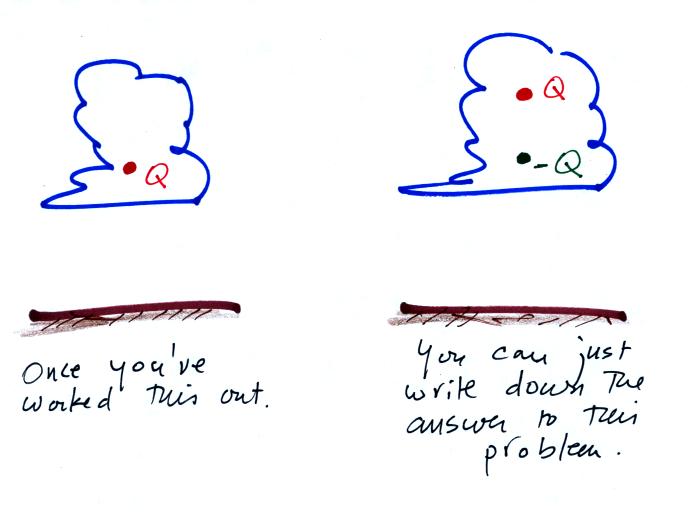
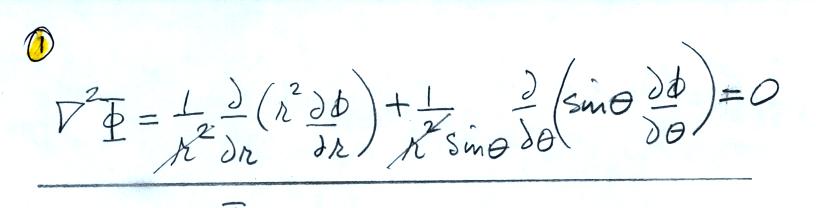A handout was distributed in class showing how the electric field in the vicinity of a conducting sphere could be determined by solving Laplace's equation.
This first page shows the geometry.  Spherical polar coordinates are used, there is azimuthal symmetry, so the potential and the electric field will depend on r and theta only.
The notes below add a few details and show how the equation at Point 1 above was obtained.
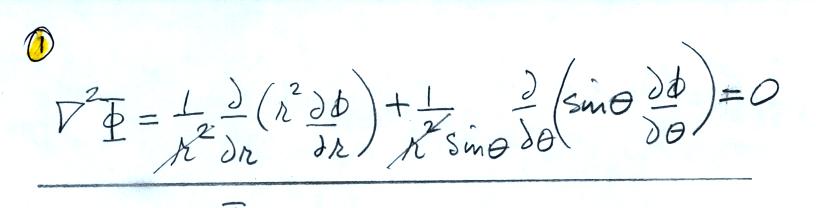
You substitute into the equation for the Laplacian in spherical polar coordinates (on a handout distributed in class last Tuesday).  The 1/r2 term cancels.
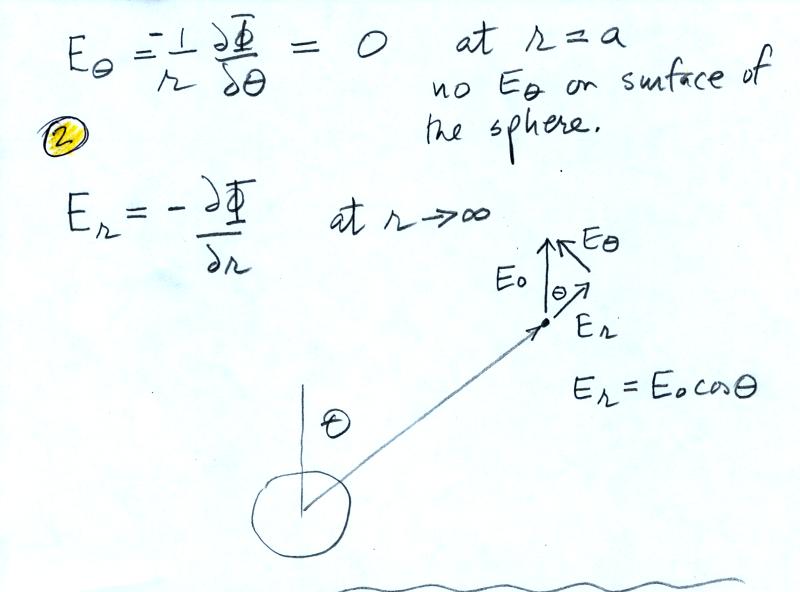
Here is some additional explanation of the two boundary conditions at Point 2 above.



The following notes fill in some of the missing details in Point 3 above.




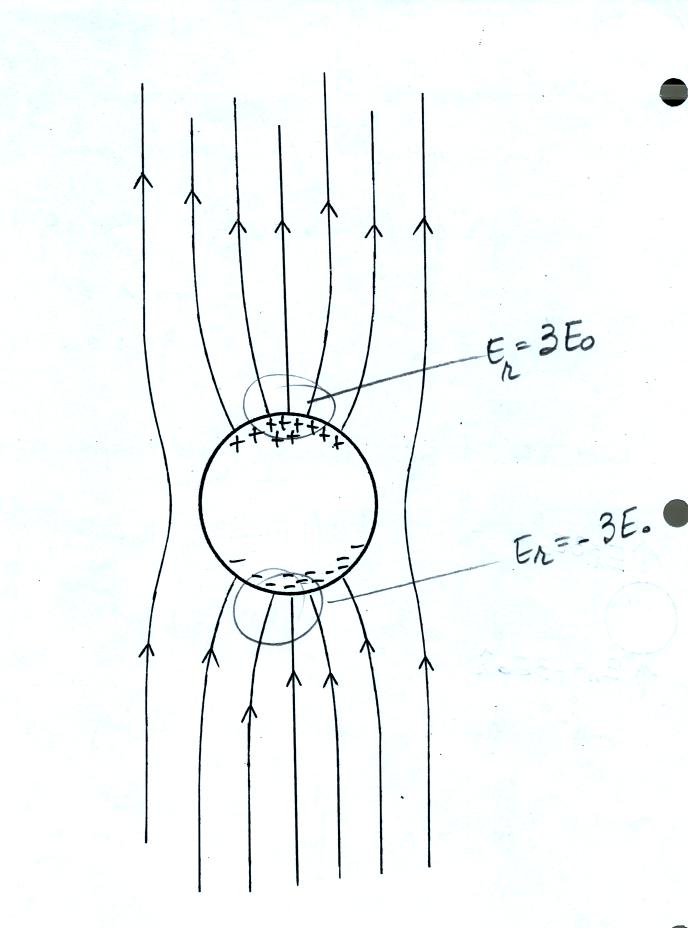
This figure gives you a rough idea of how the field is changed in the vicinity of the sphere.  E field lines must intersect the sphere perpendicularly. The field is enhanced (amplified) by a factor of three at the top and bottom of the sphere.
Enhancement of fields by conducting objects is an important concern.  In some cases (we'll look at an example or two later) the enhanced field is strong enough to initiate or trigger a lightning discharge.

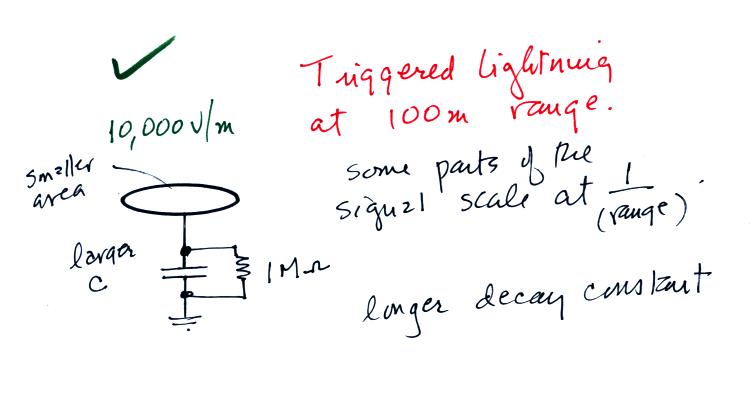
The following handout gives a rough, back-of-the-envelope kind of estimate of the factor of enhancement.
This might require a little explanation.
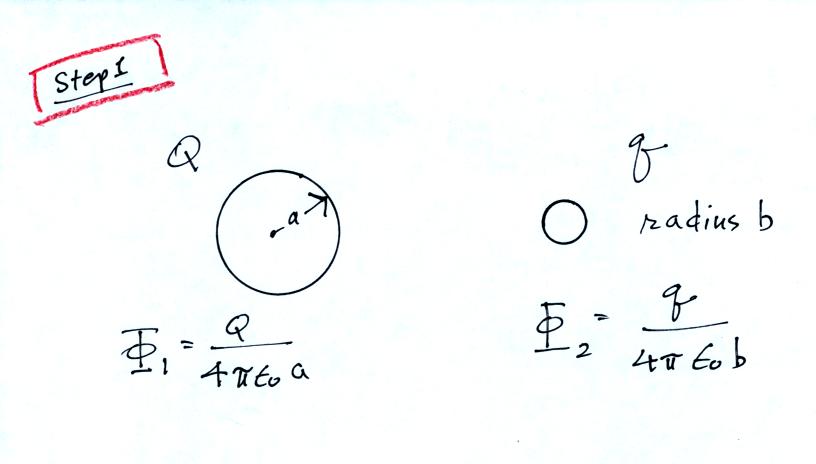
First you write down the potential at the surface of two conducting spheres of radius a and b, carrying charges Q and q.
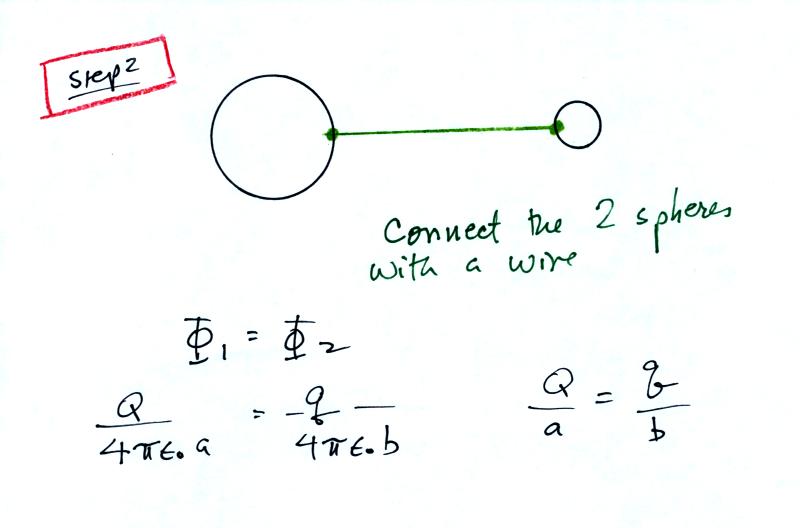
Then you connect the two spheres with a wire and force the two potentials to be equal (of course this would cause the charge to rearrange itself, but we will ignore that).
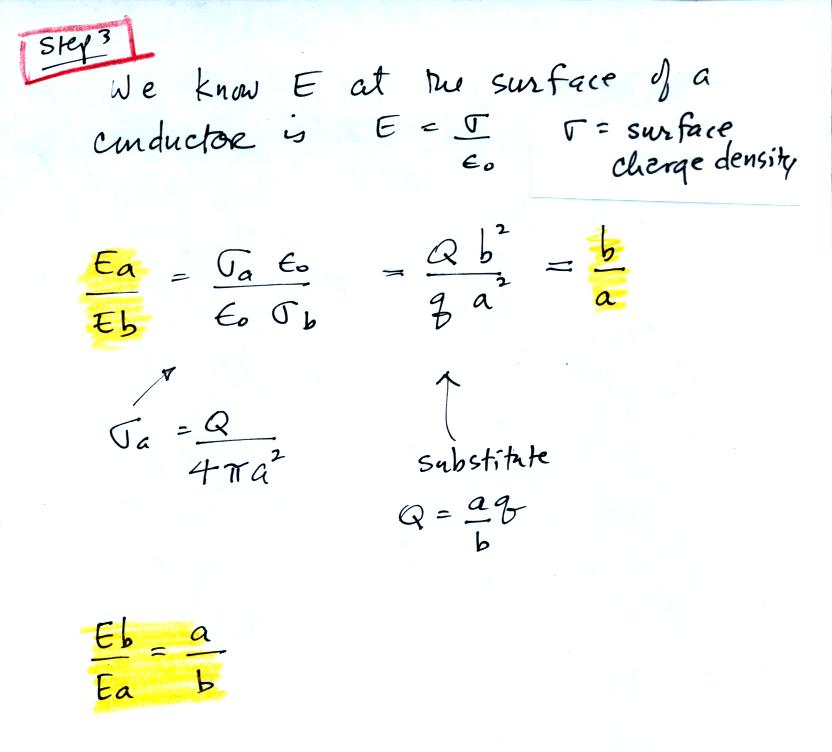
Finally we write down expressions for the relative strengths of the electric fields at the surfaces of the two spheres.  We see that the field at the surface of the smaller sphere is a/b times larger than the field at the surface of the bigger sphere.

Here is a real example of field enhancement that lead to triggering of a lightning strike and subsequent loss of a launch vehicle (you'll find the entire article here)



In this case the rocket body together with the exhaust plume created a long pointed conducting object.  Enhanced fields at the top and bottom triggered lightning.

Lighning is sometimes triggered at the tops of tall mountains

Note the direction of the branching.  This indicates that this discharge began with a leader process that traveled upward from the mountain.  Most cloud to ground lightning discharges begin with a leader that propagates from the cloud downward toward the ground.  We will of course look at the events that occur during lightning discharges in a lot more detail later in the semester.   

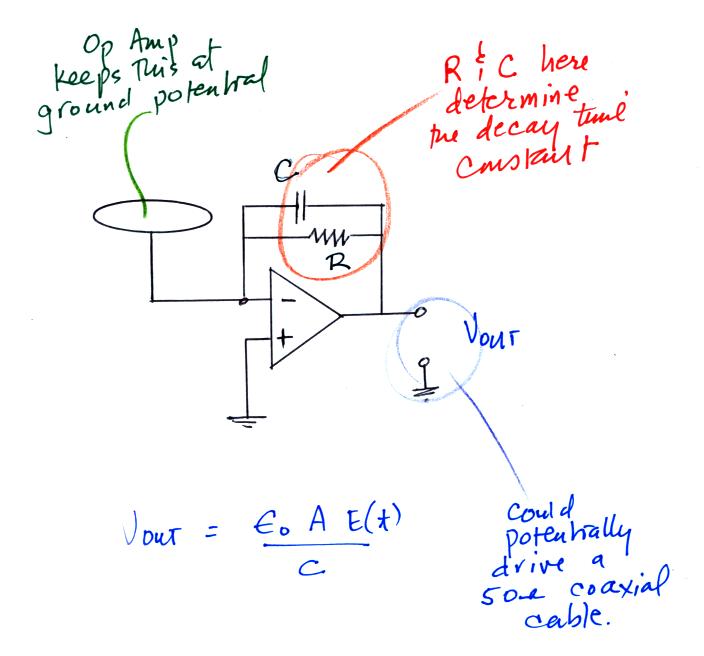
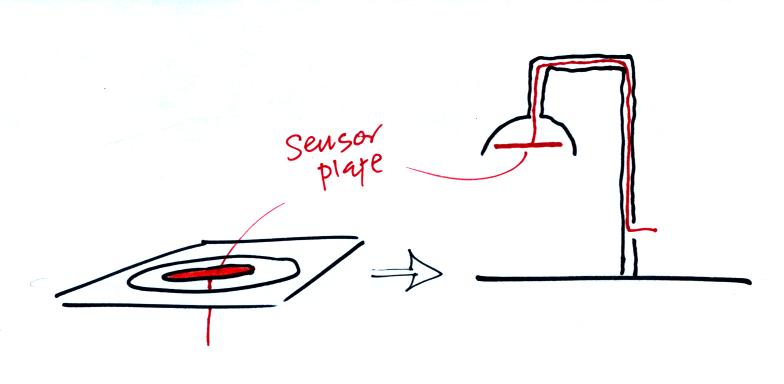
Here's an example of a very cleverly designed instrument that could be used to measure electric fields above the ground and inside thunderstorms.  Two metal spheres are attached to a horizontal insulating tube. 

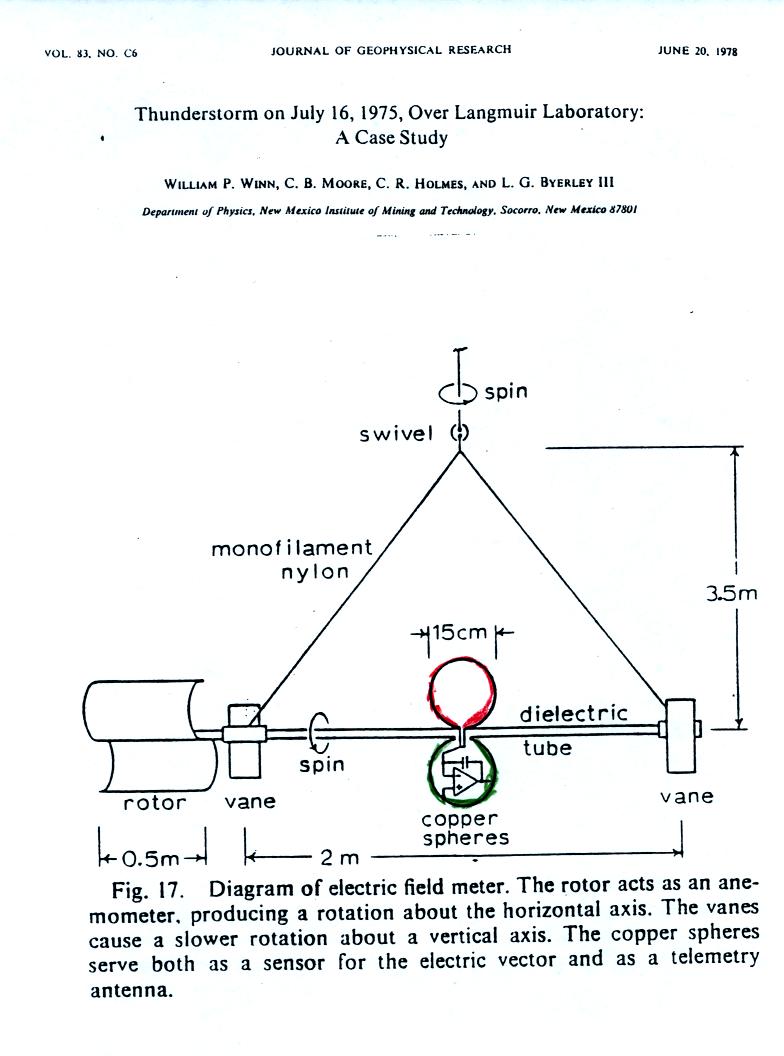
A rotor causes the two spheres (colored red and green to distinquish between them) to spin as the balloon moves upward.

As the spheres spin, a current will move back and forth between them.  The amplitude of the current will depend on the charge induced on the spheres by the electric field.

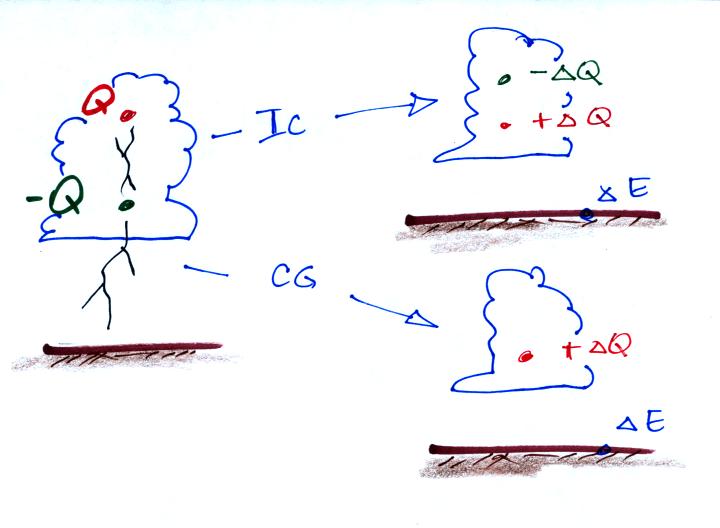
We didn't have time to carefully discuss what follows.  We'll come back to it briefly next Tuesday.  I include it here because you do an essentially identical calculation in Problem #1 on your homework assignment.

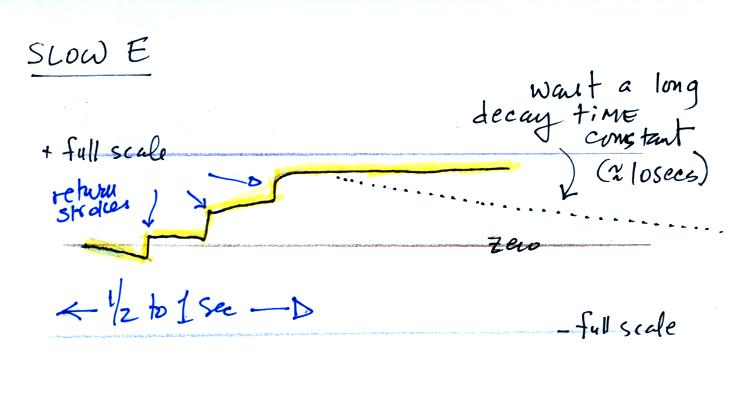
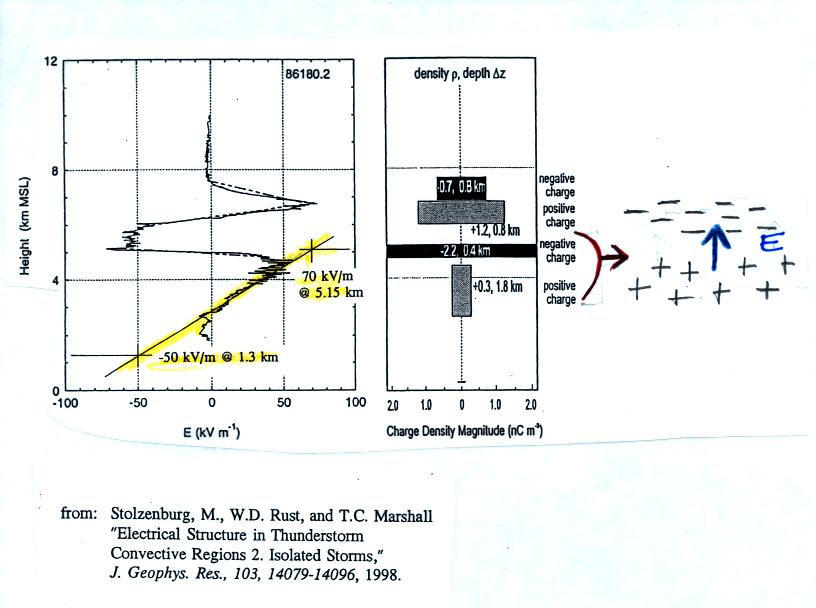
The next figure shows an example of data obtained with an instrument like this (it is from a different paper).  This was on a handout distributed in class.

The vertical field swings between large negative and positive values (tens of kilovolts/meter) as the field mill passes through layers of positive and negative charge in a thunderstorm cloud.  We use the E field data between 1.3 and 5.15 km altitude below to derive an estimate of the average volume space charge density in the bottom layer of positive charge.


The value we obtain (0.27 nC/m3) is in good agreement with the value given in the paper.