Friday Apr. 8, 2011
click here to download today's notes in a more printer friendly format

Some music from the Andrea Bocelli Live in Tuscany DVD ("Hungarian Rhapsody No. 2 in C sharp minor" performed by Lang Lang, "La Voce del Silenzio" with Andrea Bocelli and Elisa, and "Dancing" sung by Elisa)

The 1S1P Assignment #2 reports were collected today.  There is a new 1S1P Bonus Assignment due next Friday (Apr. 15).  There'll be a 1S1P Assignment #3 available soon.  That will most likely be the last 1S1P assignment of the semester.

Quiz #3 was returned in class today.  The average score was a little lower than the two previous quizzes but that seems to happen every semester.  In last Fall's 2 pm class, Quizzes 1, 2, 3, and 4 averaged 80%, 79%, 71%, and 79%, respectively.  I expect there will be a big increase in the average grade on Quiz #4 this semester also (Quiz #4 is Wed. Apr. 27). 

The is a new Optional Assignment due by 5 pm next Monday.  You'll find a link to the assignment at the end of today's notes.

We started by finishing up the last couple of steps in the "Understanding why winds blow the way they do in 10 easy steps" topic that we began last Monday.  We learned then that upper level winds blow parallel to the contour lines.  Today we tried to understand why surface winds blow across the contour lines (always toward low pressure).


The top figure shows upper level winds blowing parallel to straight contours.  The PGF and CF point in opposite directions and have the same strength.  The net force is zero.  The winds would blow in a straight line at constant speed.  Since the CF is perpendicular and to the right of the wind, this is a northern hemisphere chart.

We add friction in the second picture.  It points in a direction opposite the wind and can only slow the wind down.  The strength of the frictional force depends on wind speed (no frictional force if the wind is calm) and the type of surface the wind is blowing over (less friction when wind blows over the ocean, more frictional force when the wind is blowing over land).

Slowing the wind weakens the CF and it can no longer balance the PGF (3rd figure).  The stronger PGF causes the wind to turn and start to blow across the contours toward Low.  This is shown in the 4th figure.  Eventually the CF and Frictional force, working together, can balance out the PGF.

 What we've learned from the straight contour example, namely that the winds will blow across the contours toward low pressure can be applied to a curved contour pattern.


If you take a small little piece of a curved pattern and magnify it, it will look straight.  This is shown above.


Here is Step #10.  It is easy to figure out which of the figures are centers of low pressure.  The winds are spiralling inward in the top and bottom examples (1 and 3).  These must be surface centers of low pressure.  The winds are spiraling outward from the centers of high pressure (2 and 4).

Now you probably don't want to figure out which of these are northern and which are southern hemisphere pictures.  It is probably best to remember one of the pictures.  Remember in 1, for example, that surface winds spin counterclockwise and spiral inward around centers of low pressure in the northern hemisphere (something we learned early in the semester).  Then remember that winds spin in the other direction and blow outward around high pressure in the northern hemisphere (2).  The spinning directions of the winds reverse when you move from the northern to the southern hemisphere.  Thus you find clockwise spinning winds and inward motion around low pressure (3) and counterclockwise and outward spiraling winds around high pressure in the southern hemisphere.

Converging winds cause air to rise.  Rising air expands and cools and can cause clouds to form.  Clouds and stormy weather are associated with surface low pressure in both hemispheres.  Diverging winds created sinking wind motions and result in clear skies.
Next we had a short look at the cause of the Coriolis force.  Most of what follows can be found on p. 122c in the photocopied ClassNotes.



Imagine something flies over Tucson.  It travels straight from west to east at constant speed.  The next figure shows the path that the object followed as it passed over the city.  You would, more or less subconciously,  plot its path relative to the ground.



Here's the path the moving object would appear to follow relative to the ground.  Based on this straight line, constant speed trajectory you'd conclude there was no net force acting on the object.



In this second picture the object flies by overhead just as it did in the previous picture.  In this picture, however, the ground is moving (don't worry about what might be causing the ground to move).



Here's the path the object would appear to follow relative to the ground.  It's no longer moving from W to E but rather from the NW toward the SE.  It's still straight line motion at constant speed, though, so you conclude there was no net force acting on the object.


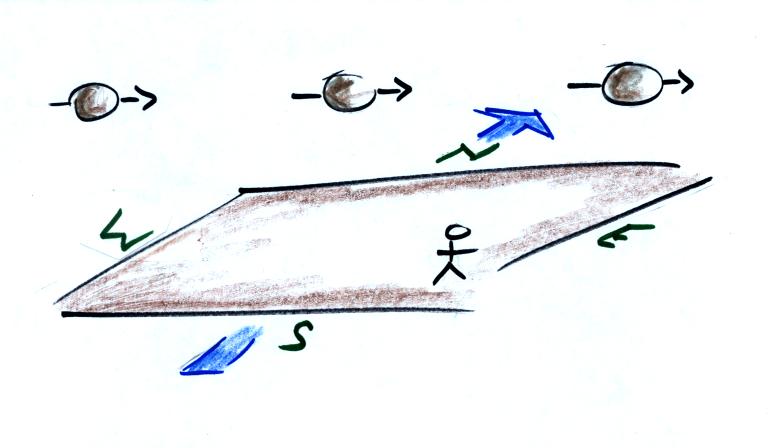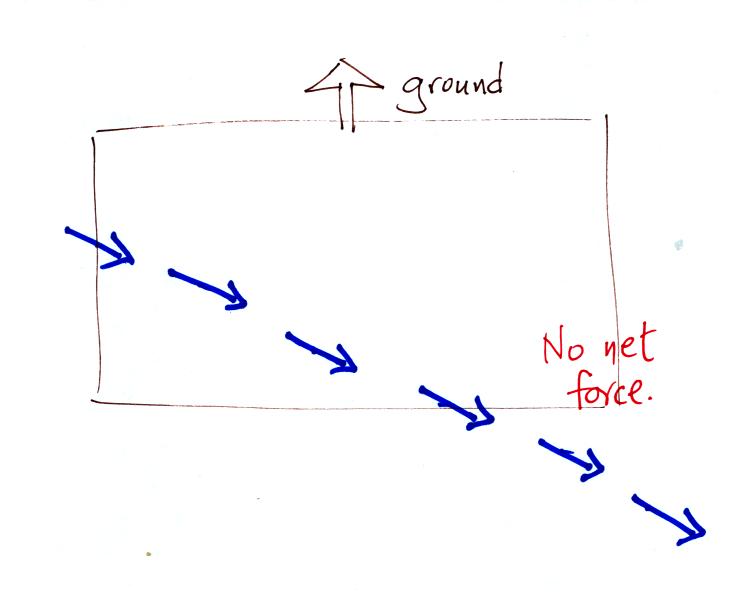
Now the ground is moving and also spinning.



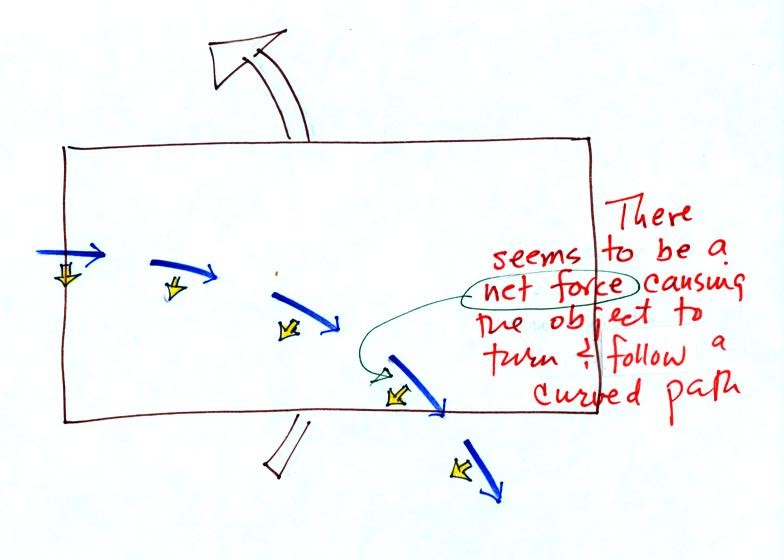
The path of the object plotted on the ground appears to be curved.  That's because the ground is spinning, but let's just ignore that for the time being.  In this case you'd conclude that there was a net force perpendicular and to the right of the moving object.  This net force would be needed to explain the curved path that the object appears to be following. 

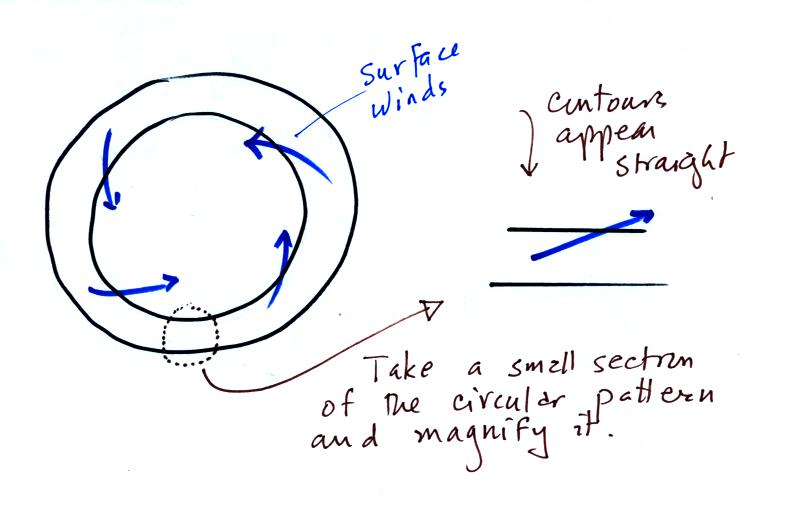
At most locations on the earth the ground IS rotating.  This is most easily seen at the poles.


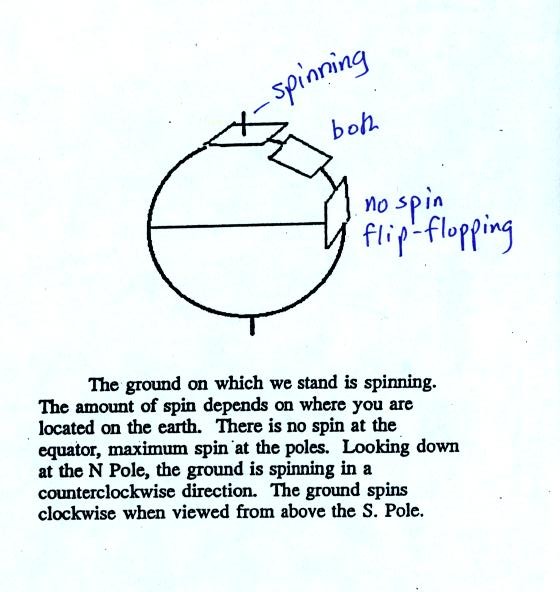
Imagine a piece of paper glued to the top of a globe.  As the globe spins the piece of paper will rotate.  A piece of paper glued to the globe at the equator won't spin, it will flip over.  At points in between the paper would spin and flip, the motion gets complicated.

The easiest thing for us to do is to ignore or forget about the fact that the ground on which we are standing is rotating.  We do still need to account for the curved paths that moving objects will take when they move relative to the earth's surface.  That is what the Coriolis force does.

And that's the reason for another 1S1P Bonus Assignment.  This was a demonstration that proved that the ground we're standing on (at most locations on earth) is spinning.  Here's a photograph of a Foucault Pendulum at the Pantheon in Paris.

It seemed appropriate at this point to look at a common misconception involving the Coriolis force.  You might already have heard that water spins in a different direction when it drains from a sink or a toilet bowl in the southern hemisphere than it does in the northern hemisphere.  You might also have heard that this is due to the Coriolis force or the Coriolis effect. 

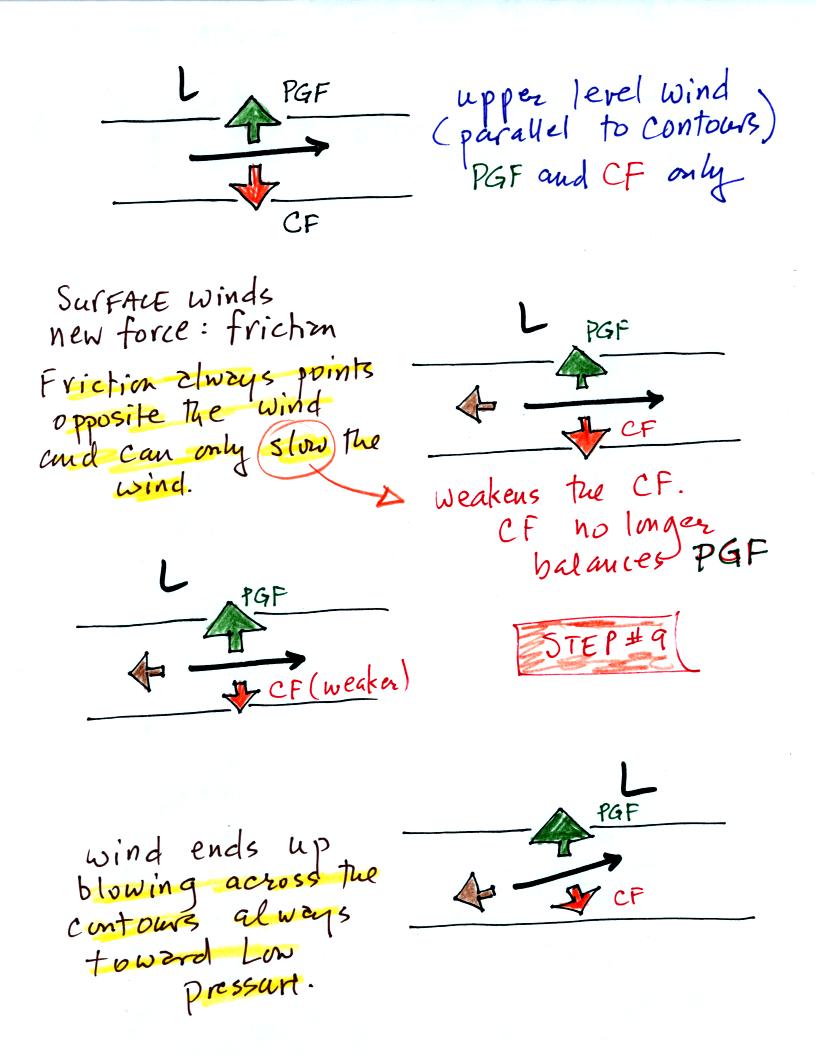
The Coriolis force does cause winds to spin in opposite directions around high and low pressure centers in the northern and southern hemisphere.  The PGF starts the air moving (in toward low, out and away from high pressure) then the Coriolis force bends the wind to the right (N. hemisphere) or to the left (S. hemisphere).

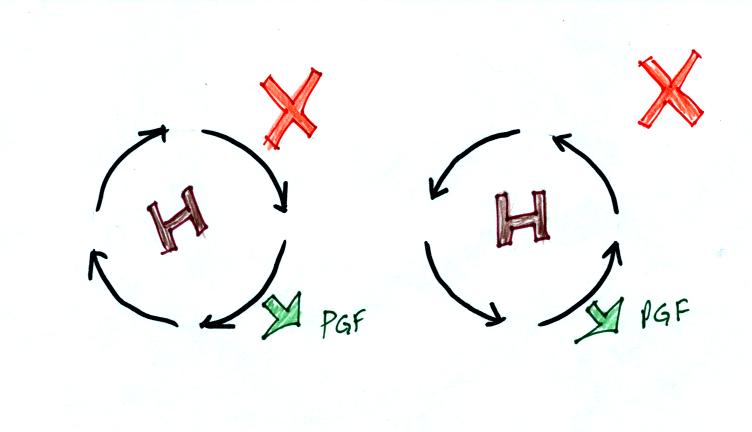
Here's what you end up with in the case of low pressure (you'll find these figures on p. 130 in the photocopied ClassNotes):


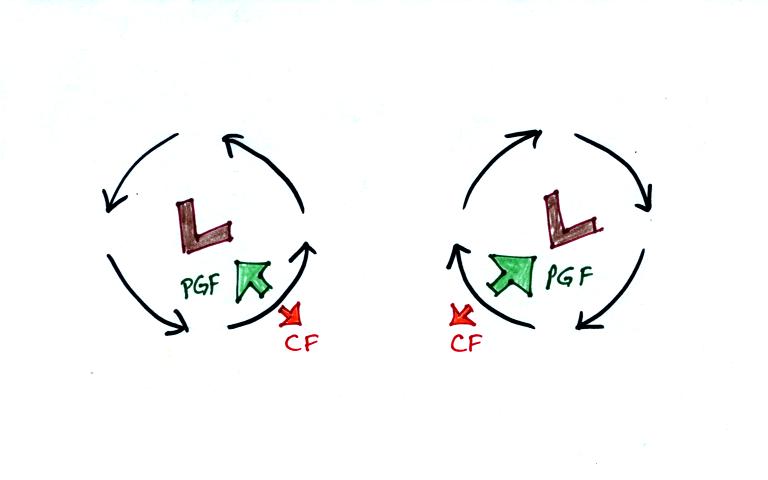
Air starts to move inward toward low pressure.  Then the Coriolis force causes it to turn to the right or left depending on which hemisphere you're in.  You should be able to say which of the pictures above is the northern hemisphere and which is the southern hemisphere picture.


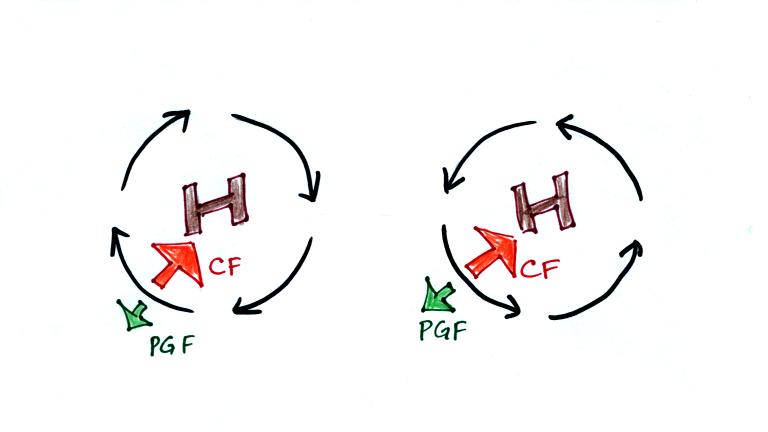
The same kind of idea applies to high pressure except that the air starts moving outward.  The Coriolis force then turns it to the right or left.

There are situations where the PGF is much stronger than the CF and the CF can be ignored.  A tornado is an example.  Winds can blow around Low pressure because the PGF points inward.


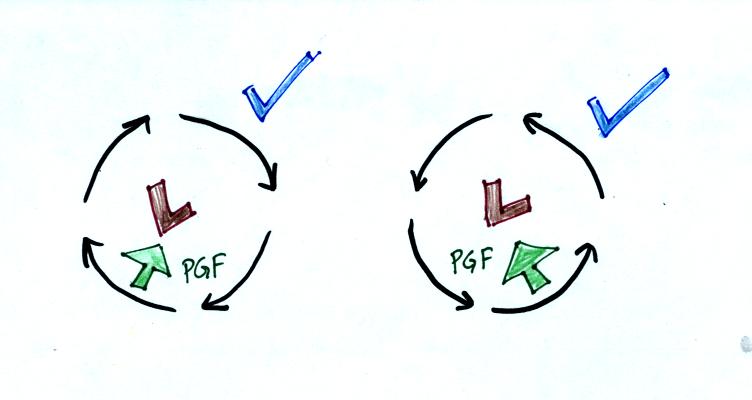
The wind can spin in either direction in either hemisphere.

Without the CF winds can't spin around High pressure because there is nothing to provide the needed inward force.


What about water draining from sinks, buckets, toilets etc.


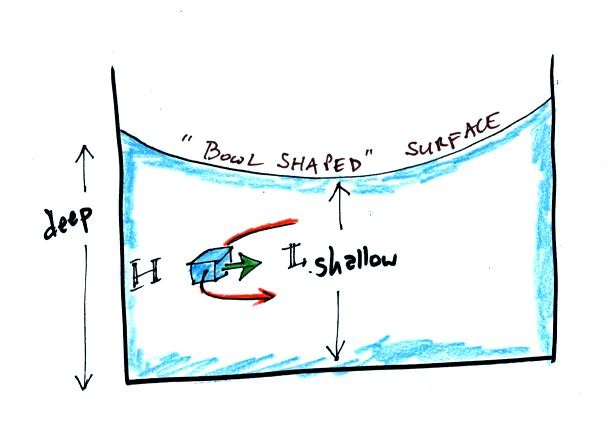
There's just an inward pointing PGF, no CF.  Water can spin in either direction in either hemisphere.  What causes the inward pointing PGF?  The water at the end of the spinning water is a little deeper than in the middle.  Since pressure depends on weight, the pressure at the outer edge of the spinning water is higher than in the center.

Water draining from a sink or toilet can spin in either direction.  It doesn't matter where you're located. 

We watched a short video segment that seemed to show otherwise.  In the video a young man living at the Equator in Kenya was demonstrating the Coriolis effect to tourists.  He showed water draining from a bucket and spinning in opposite directions depending on whether he was north or south of the equator.  The water seemed to drain without spinning at all right at the equator.

Don't believe everything you see on video.  The gentleman in the video was just very good at getting the draining water to spin one direction or another as he moved on opposite sides of the equator.  Probably the most difficult part would be to get the water draining without spinning, which is what he was able to do when standing right on the equator.

But this something we should probably checkout for ourselves, so here is one of my favorite optional assignments of the semester.