Tomato seedlings (the small guys in back are peppers) growing on the warm sunny window sill in my office.  This will come up during the course of today's class.

---

It is easy to lose sight of the main concepts because there are so many details.  The following (found on pps 43&44 in the photocopied Class Notes) is meant to introduce some of what we will be covering in class.  (some of the figures that follow are from a previous semester and may differ somewhat from what we did in class)

Types of energy
We will learn the names of several different types or forms of energy. Kinetic energy is energy of motion. Some examples (both large and microscopic scale) are mentioned and sketched above.  This is a relatively easy to visualize and understand form of energy.

Latent heat energy is perhaps the most underappreciated and most confusing type of energy. The word latent refers to energy that is hidden in water and water vapor.  The hidden energy emerges when water vapor condenses or water freezes (the energy had been added earlier when ice was melted or water was evaporated).

Radiant energy is a very important form of energy that was for some reason left off the original list.  Sunlight is an example of radiant energy that we can see and feel (you feel warm when you stand in sunlight).  There are many types of radiant energy that are invisible.  Electromagnetic radiation is another name for radiant energy.

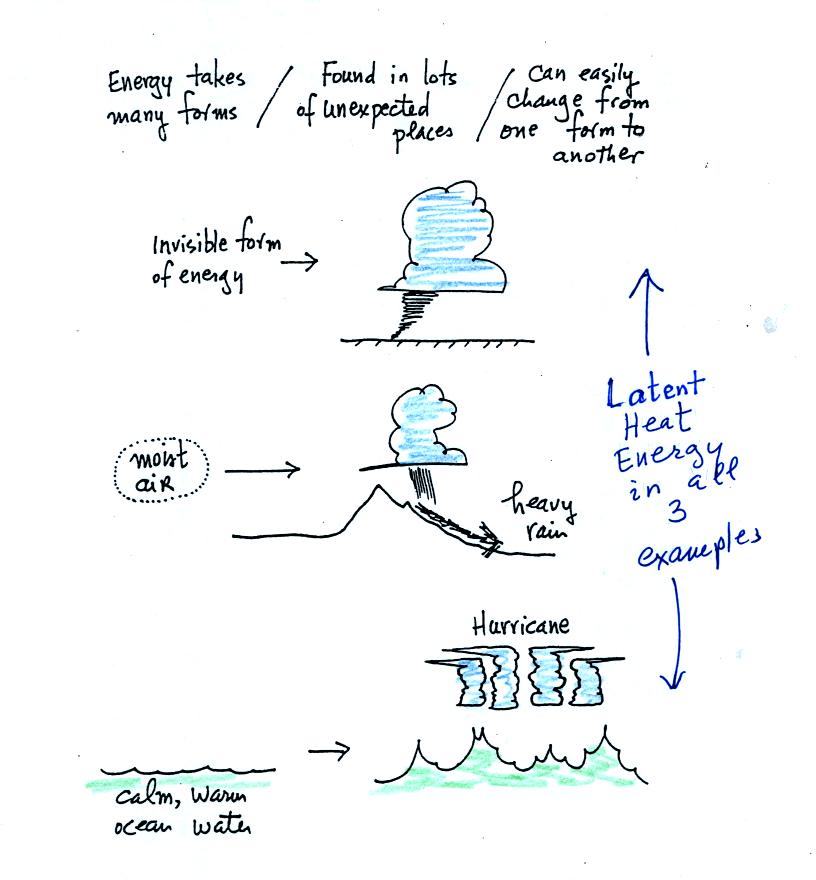
Water vapor is effectively a particularly important form of invisible energy.  When water vapor condenses to produce the water droplets (or ice crystals) in a cloud, an enormous amount of latent heat energy is released into the atmosphere. 

It is hard to visualize or appreciate the amount of energy released into the atmosphere during condensation.  You can imagine the work that you would need to do to carry a gallon of water (8 pounds) from Tucson to the top of Mt. Lemmon.  To accomplish the same thing Mother Nature must first evaporate the water and (if my calculations are correct) that requires about 100 times the energy that you would use to carry the 8 pounds of water to the summit of Mt. Lemmon.  And Mother Nature transports a lot more than just a single gallon.

Energy transport
Four energy transport processes are listed below.

 

By far the most important process is energy transport in the form of electromagnetic radiation (sunlight is a common form of electromagnetic radiation).  This is the only process that can transport energy through empty space.  Electromagnetic radiation travels both to the earth (from the sun) and away from the earth back into space.  Electromagnetic radiation is also responsible for about 80% of the energy transported between the ground and atmosphere.

You might be surprised to learn that latent heat is the second most important transport process.

Rising parcels of warm air and sinking parcels of cold air are examples of free convection.  Because of convection you feel colder or a cold windy day than on a cold calm day.  Ocean currents are also an example of convection.  Ocean currents transport energy from the warm tropics to colder polar regions.  Not all of these details were mentioned in class.

Remember that convection is one of the ways of causing rising air motions in the atmosphere (convergence into centers of low pressure, fronts, and orographic or topographic lifting were the other ways). 

Conduction is the least important energy transport at least in the atmosphere.  Air is such a poor conductor of energy that it is generally considered to be an insulator.

Energy balance and the atmospheric greenhouse effect
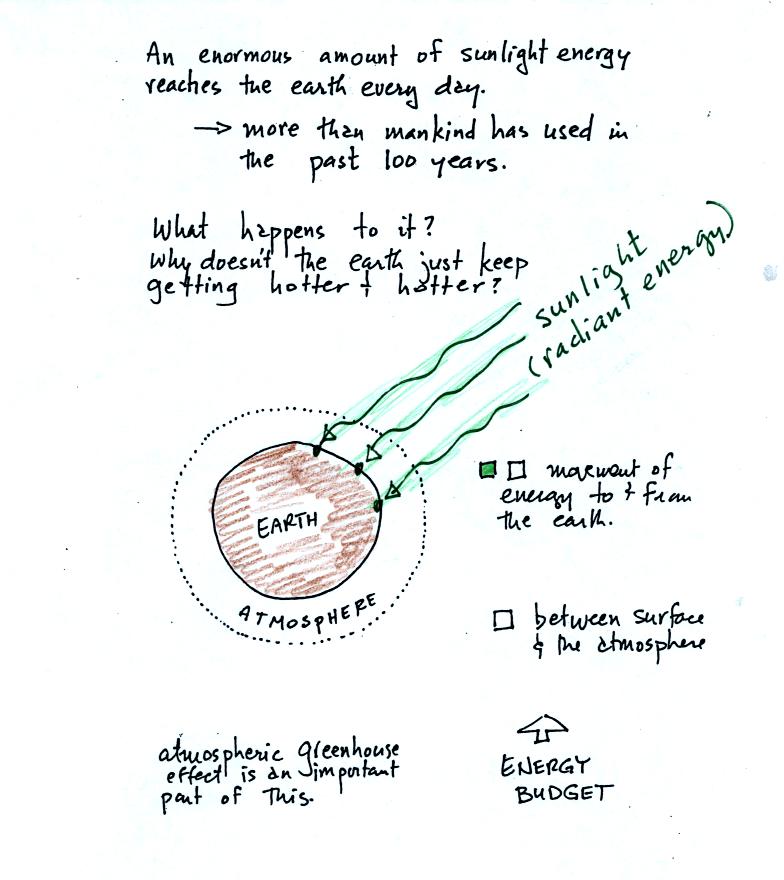
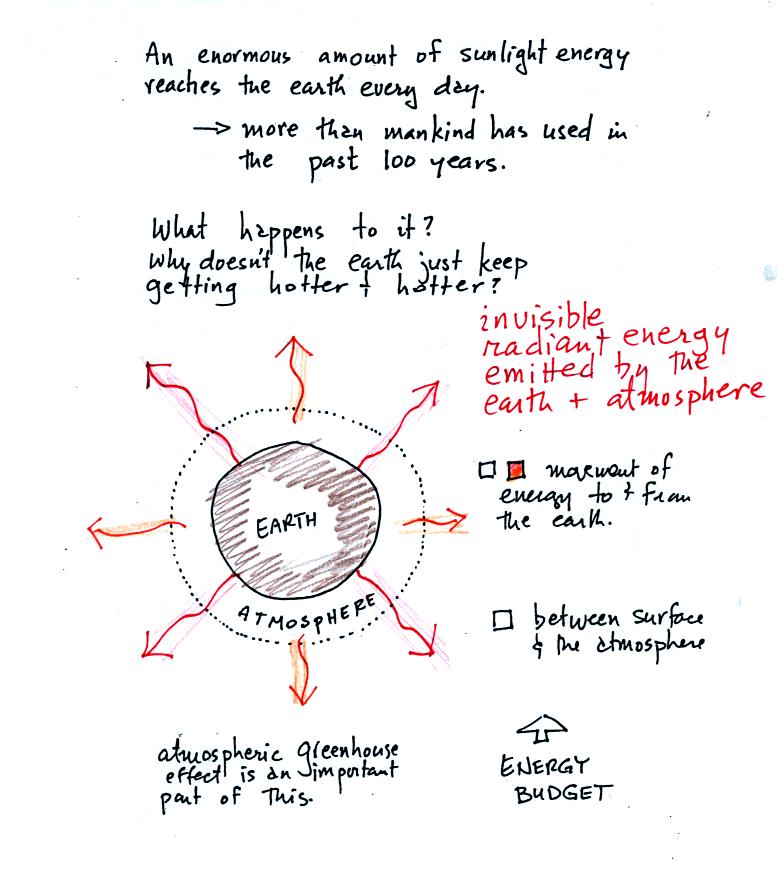
The next picture (the figure drawn in class has been split into three parts for improved clarity) shows energy being transported from the sun to the earth in the form of electromagnetic radiation.

We are aware of this energy because we can see it (sunlight also contains invisible forms of light) and feel it.  With all of this energy arriving at and being absorbed by the earth, what keeps the earth from getting hotter and hotter?  The answer is that the earth also sends energy back into space (the orange and pink arrows in the figure below)

This infrared light is an invisible form of energy (it is weak enough that we don't usually feel it either).  A balance between incoming and outgoing energy is achieved and the earth's annual average temperature remains constant.

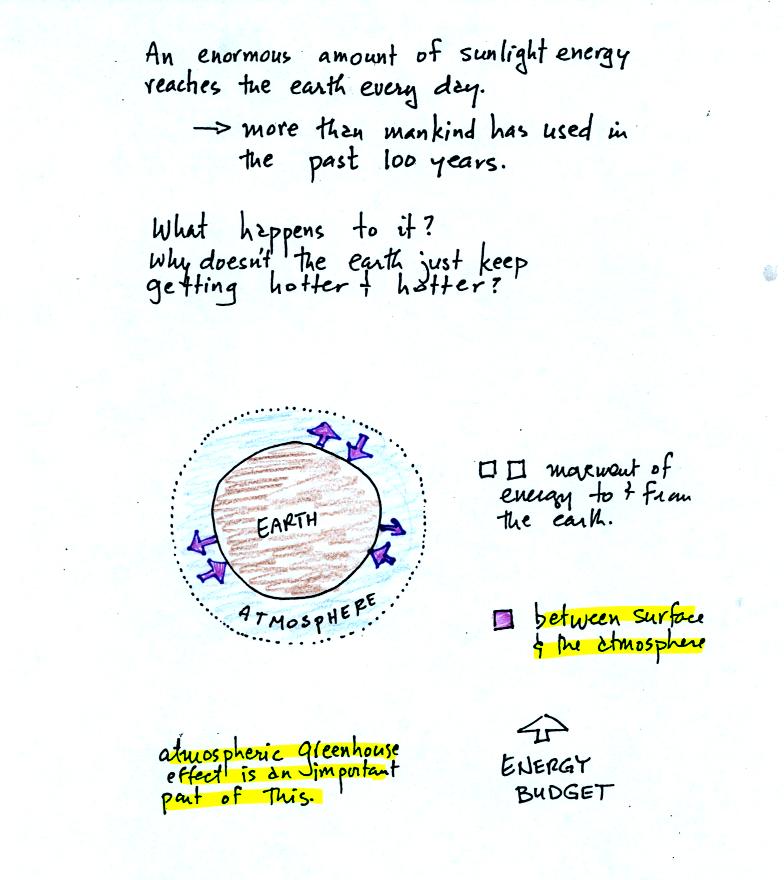
We will also look closely at energy transport between the earth's surface and the atmosphere. This is where latent heat energy transport, convection and conduction operate (they can't transport energy beyond the atmosphere and into outer space).

That is also where the atmospheric greenhouse functions.  That will be a important goal - to better understand how the atmospheric greenhouse effect works.

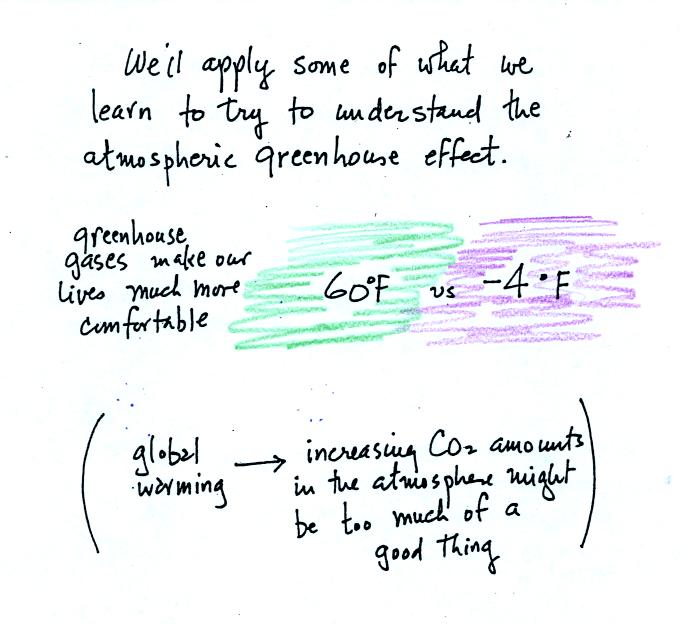
The greenhouse effect is getting a lot of "bad press".  If the earth's atmosphere didn't contain greenhouse gases and if there weren't a greenhouse effect, the global annual average surface temperature would be about 0 F (scratch out -4 F and put 0 F, it's easier to remember).  Greenhouse gases raise this average to about 60 F and make the earth a much more habitable place.  This is the beneficial aspect of the greenhouse effect.

The detrimental side is that atmospheric greenhouse gas concentrations are increasing.  This might enhance the greenhouse effect and cause the earth to warm.  While that doesn't necessarily sound bad it could have many unpleasant side effects.  That's a subject we'll explore briefly later in the semester.

---

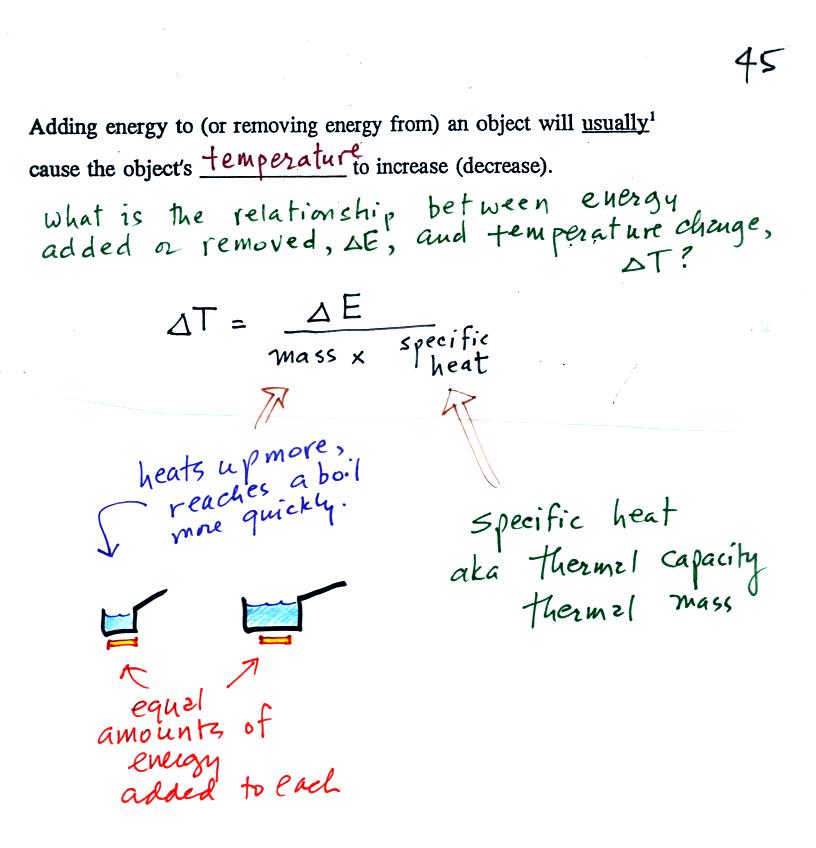
When you add energy to an object, the object will usually warm up (conversely when you take energy from an object the object will cool).  It is relatively easy to come up with an equation that allows you to figure out what the temperature change will be (one of those equations I'll probably write on the board during the next quiz - try to understand it, you don't have to memorize it).


The temperature change will first depend on how much energy was added.  This is a direct proportionality, so delta E is in the numerator of the equation (delta E and delta T are both positive when energy is added, negative when energy is taken from something)

When you add equal amounts of energy to large and small  pans of water, the small pan will heat up more quickly.  The temperature change, delta T, will depend on the amount of water, the mass.  A small mass will mean a large delta T, so mass should go in the denominator of the equation. 

Different materials react differently when energy is added to them.  A material with a large specific heat will warm more slowly than a material with a small specific heat.  Specific heat has the same kind of effect on delta T as mass.  Specific heat is sometimes called "thermal mass" or "thermal capacity."  You can think of specific heat as being thermal inertia - a substance with high specific heat, lots of thermal inertia, will be reluctant to change temperature.

Here's an important example that will show the effect of specific heat (middle of p. 45)

Equal amounts of energy (1000 calories, note that calories are units of energy) are added to equal masses (100 grams) of water and soil.  We use water and soil in the example because most of the earth's surface is either ocean or land. Water has a higher specific heat than soil, it only warms up 10^o C.  The soil has a lower specific heat and warms up 40^o C, 4 times more than the water (there is a factor of 4 difference in the specific heats of water and soil).

These different rates of warming of water and soil have important effects on regional climate.


Oceans moderate the climate.  Cities near a large body of water won't warm as much in the summer and won't cool as much during the winter compared to a city that is surrounded by land.
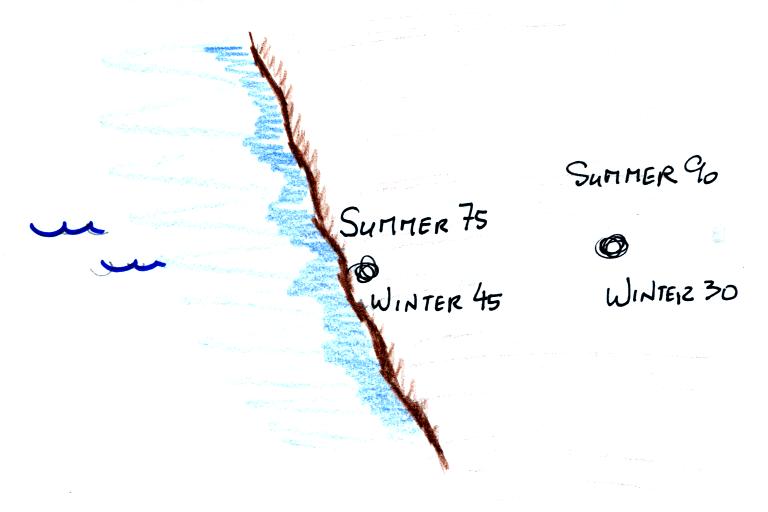
The yearly high and low monthly average temperatures are shown at two locations above.  The city on the coast has a 30^o F annual range of temperature (range is the difference between the summer and winter temperatures).  The city further inland (assumed to be at the same latitude and altitude) has an annual range of 60^o F.  Note that both cities have the same 60^o F annual average temperature.  We'll see a much more dramatic example of the moderating effect of water on climate in a couple of weeks.

Here's another situation where you can take advantage of water's high specific heat to moderate "micro climate."

Here are some tomatoes being planted in early February in my vegetable garden a winter or two ago.  It still gets plenty cold enough at night to kill tomatoes (the brocolli and lettuce in the background can handle a light frost) so you have to protect the tomatoes.

Here's one way of doing that.  You can surround each plant with a "wall of water"  -  a tent like arrangement that surrounds each plant.  The cylinders are filled with water and they take advantage of the high specific heat of water and won't cool as much as the air or soil would during a cold night.

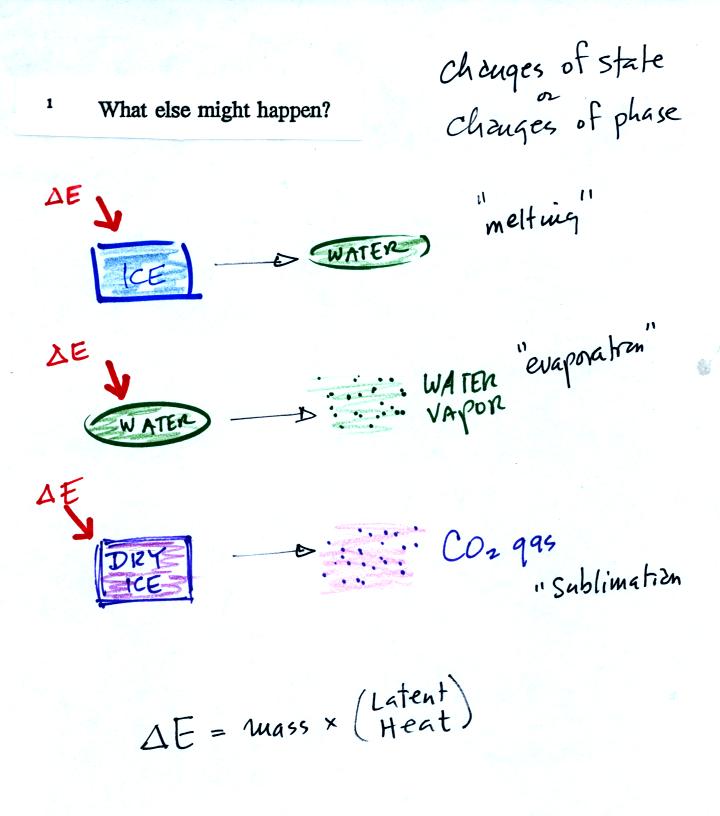
Adding energy to an object will usually cause it to warm.  But there is another possibility (bottom p. 45),  the object could change phase (change from solid to liquid or gas).  Adding energy to ice might cause the ice to melt.  Adding energy to water could cause it to evaporate.  The figure below is a little more detailed version of what was drawn in class.

The equation at the bottom of the figure above allows you to calculate how much energy is required to melt ice or evaporate water or sublimate dry ice.  You multiply the mass by the latent heat, a variable that depends on the particular material that is changing phase. 

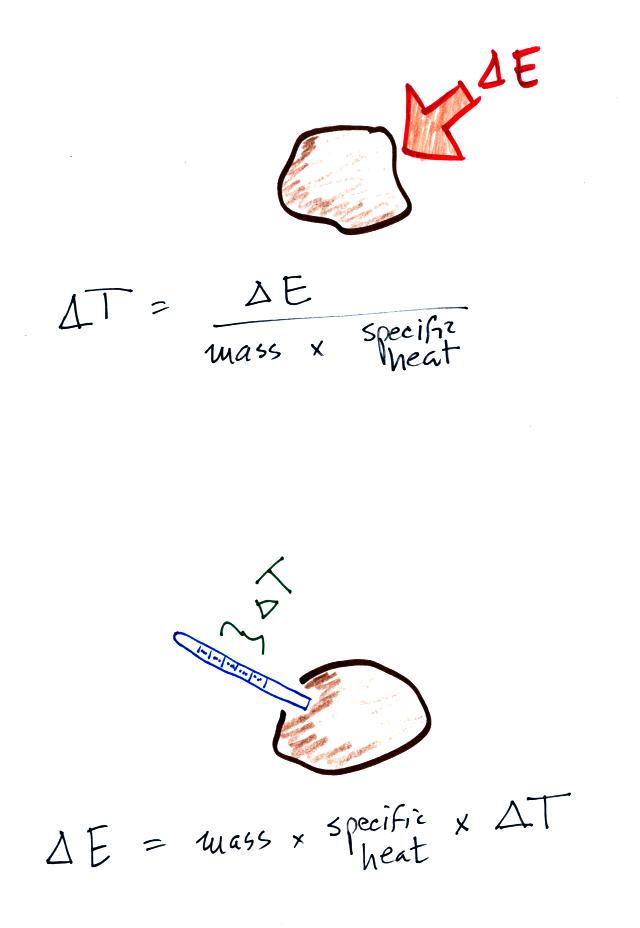
If you add energy to or remove energy from an object, the object will usually change temperature.  You can calculate the temperature change if you know the object's mass and its specific heat.  That's the equation we used in the example calculation above.

We will be using the equation next in a slightly different way in a class experiment/demonstration. We will measure the temperature change of a small cup of water and use that to determine the amount of energy lost by the water.

---

A couple of students from the class were nice enough to volunteer to perform the experiment.

The object of the experiment was to measure the latent heat of vaporization of liquid nitrogen.  That just means measuring the amount of energy needed to evaporate a gram of liquid nitrogen.  The students that are doing Experiment #2 are measuring the latent heat of fusion of ice, the energy needed to melt one gram of ice.  You'll find the following figure on p. 45a in the photocopied Classnotes.

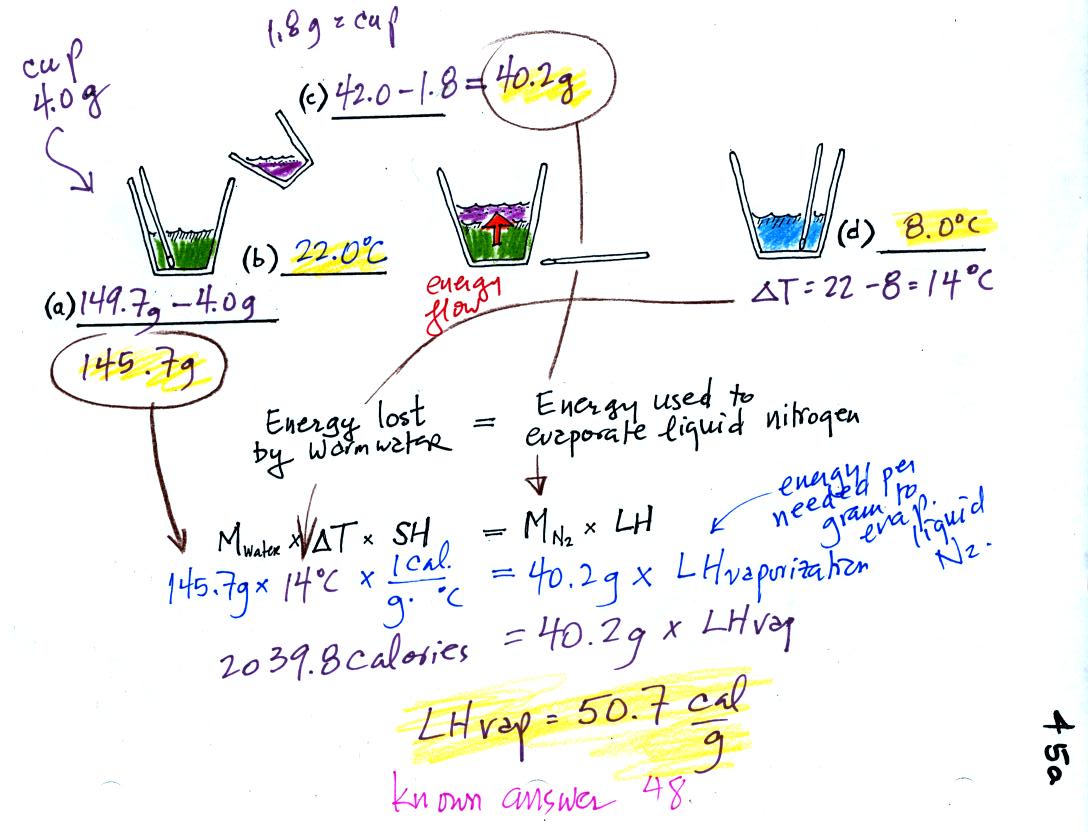
(a)
Some room temperature water poured into a styrofoam cup weighed 149.7 g.  The cup itself weighed 4.0 g, so we had 145.7 g of water.

(b)
The water's temperature was 22.0 C  (room temperature).

(c)
  40.2 g of liquid nitrogen was poured into the cup of water.

It takes energy to turn liquid nitrogen into nitrogen gas.  The needed energy came from the water.  This flow of energy is shown in the middle figure above.  Because the experiment is performed in a styrofoam cup we assume that there is no energy flowing between the water in the cup and the surounding air.  All of the energy leaving the water is being used to evaporate nitrogen

(d)
After the liquid nitrogen had evaporated the water's temperature was remeasured.  It had dropped to 8.0 C.  That is a temperature drop of 22.0 - 8.0 = 14.0 C.

Because we knew how much water we started with, its temperature drop, and water's specific heat we can calculate how much energy was taken from the water.

We then divide that number by the amount of liquid nitrogen that was evaporated.