Wednesday Mar. 23, 2011
click here to download today's notes in a more
printer friendly format
Four songs from Calexico this morning with lyrics in English,
French, and Spanish (Ballad
of
Cable Hogue, Si
Tu
Disais, Alone
Again Or, Cancion
del
Mariachi).
The In-class Assignment from Monday and the 1S1P reports on UV
Light have been graded. They were returned in class today
together with Midterm Grade
Summaries (you'll find more information about the grade summaries at
the end of today's notes).
Here's more information
about the Public Forum planned for next Tuesday (Mar. 29, 6:30 pm in
Centennial Hall) on the earthquake, tsunami, and nuclear crisis in
Japan.
A new take-home
Optional Assignment was handed out in class today. It is due
by the start of class next Monday, Mar. 28.
Here's a review of the humidity variables that were introduced on
Monday.
mixing ratio (r)
actual amount of water vapor
in the air
saturation mixing ratio (rs)
maximum amount of water vapor
that can be in the air (depends on temp.)
relative humidity (RH)
how close is the air to being
"filled" to capacity or saturated with water vapor
dew point (Td)
1. gives an idea of the
actual amount of water vapor in the air
2. cooling the air to the dew point raises the RH to 100%
Most of the period was spent working out some humidity
example problems.
This
way
you
will
learn more about the 4 humidity variables; you'll see what they do
and what can cause
their values to change.
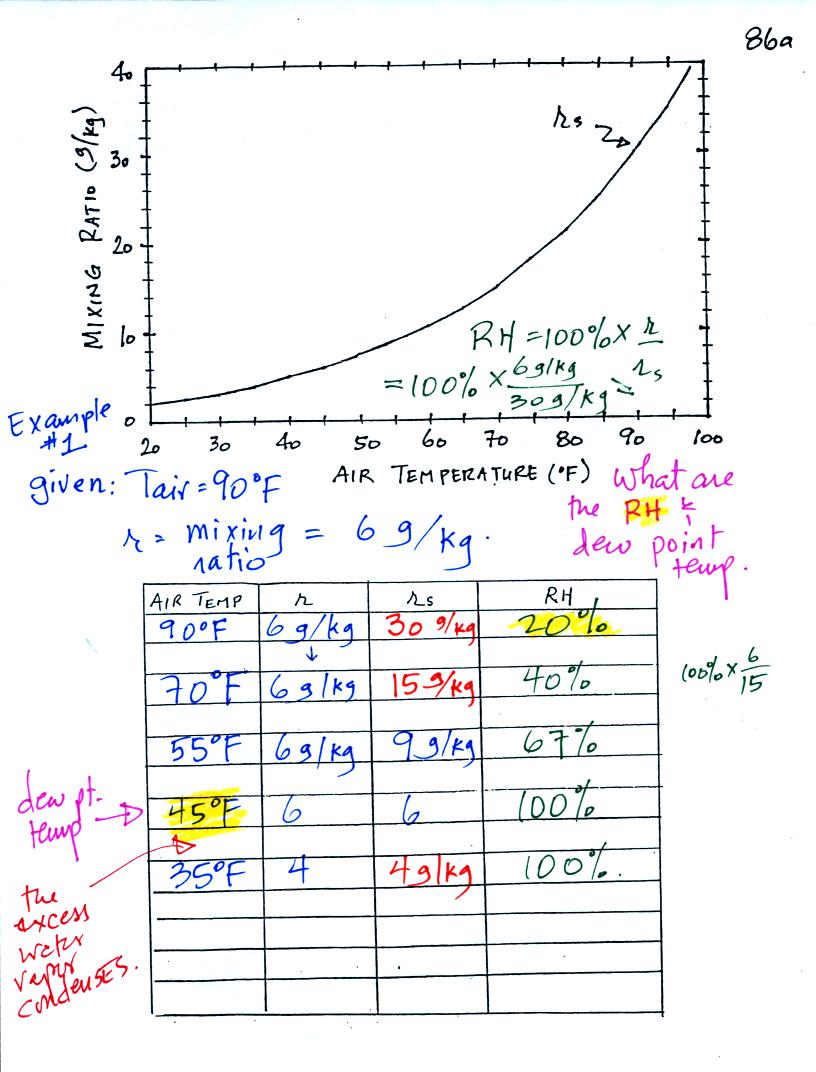
Example 1
Here is the first sample
problem that we worked in
class. You will have a hard time unscrambling this if
you're seeing it for
the first
time. The series of steps that we followed are retraced
below:
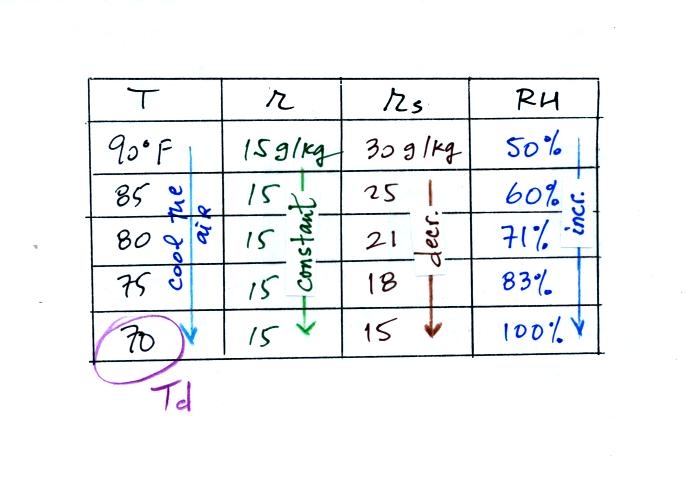
We're given an air temperature of 90 F and a mixing ratio
(r) of 6
g/kg.
We're supposed to find the relative humidity (RH) and
the dew point temperature.
We start by entering the data we were given in the
table. Once
you know the air's temperature you can look up the saturation mixing
ratio value; it is 30 g/kg for 90 F air. 90 F air could
potentially hold 30 grams of water vapor per kilogram of dry air (it
actually contains 6 grams per kilogram in this example). A table
of
saturation mixing ratio values can be found on p. 86 in the ClassNotes.
Once you know mixing ratio and saturation mixing ratio you can
calculate the relative humidity (you divide the mixing ratio by the
saturation mixing ratio, 6/30, and multiply the result by 100%).
You ought to be able to work out the ratio 6/30 in your head (6/30 =
1/5 = 0.2). The RH is 20%.
The numbers we just figured out are shown on the top line
above.
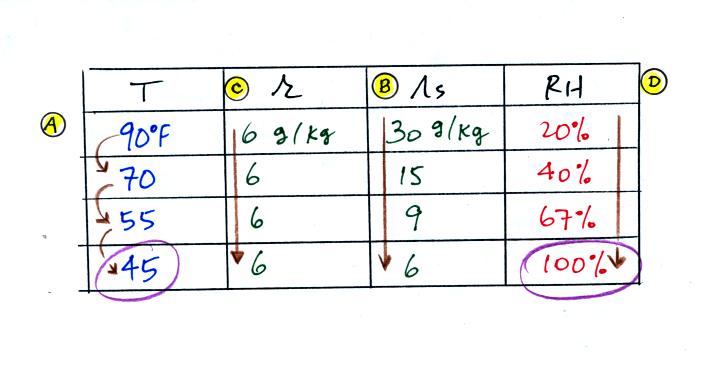
(A) We imagined cooling the air from 90F to 70F, then to 55F, and
finally to 45F.
(B) At each step we looked up the saturation mixing ratio and entered
it on the chart. Note that the saturation mixing ratio values
decrease as the air is
cooling.
(C) The mixing
ratio doesn't
change as we cool the air. The only
thing that changes r is adding or removing water vapor and we aren't
doing either.
(D) Note how the relative humidity is increasing as we cool
the
air. The air still contains the same amount of water
vapor it is
just that the air's capacity is decreasing.
Finally at 45 F the RH becomes 100%. This is kind of a special
point. You have cooled the air until it has become
saturated.
The dew point temperature in
this problem is 45 F.
What would happen if we cooled the air
further still, below the dew
point temperature?
35 F air can't hold the 6 grams of water vapor
that 45 F air can. You can only "fit" 4 grams of water vapor into
the 35 F air. The remaining 2 grams would condense. If
this happened at ground level the ground would get wet with dew.
If it happens above the ground, the water vapor condenses onto small
particles in the air and forms fog or a cloud. Now because water
vapor is being taken out of the air (and being turned into water), the
mixing
ratio will decrease from 6 to 4.
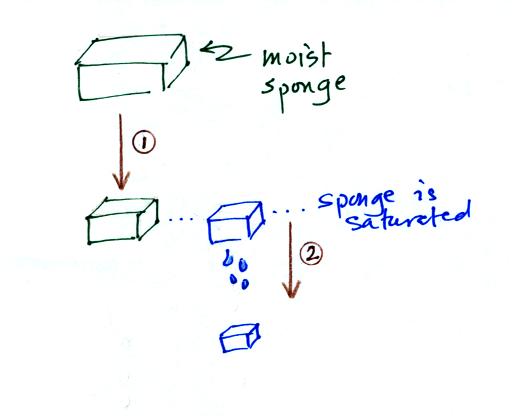
In many ways cooling moist air is liking squeezing a
moist sponge (this
figure
wasn't
shown
in
class)
Squeezing the
sponge and reducing its volume is like cooling moist air and reducing
the saturation mixing ratio. At first when you sqeeze the sponge
nothing happens, no water drips out. Eventually you get to a
point where the sponge is saturated. This is like reaching the
dew point. If you squeeze the sponge any further (or cool air
below
the dew point) water will begin to drip out of the sponge (water vapor
will condense from the air).
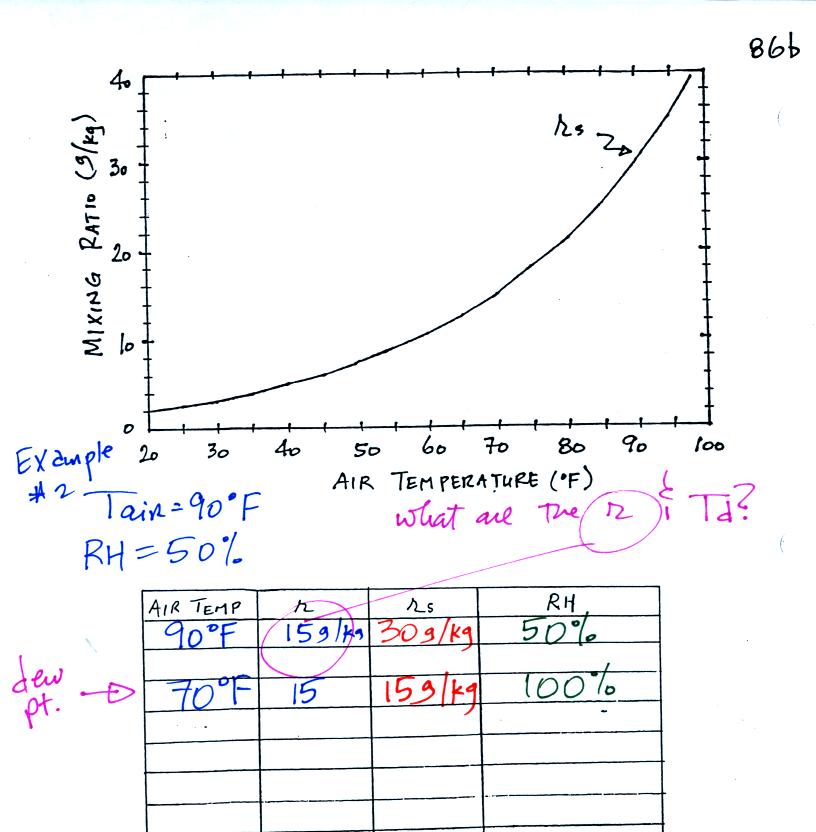
Example 2
The work that we did in class is shown above. Given an air
temperature
of 90
F and a relative humidity of 50% you are supposed to figure out the
mixing ratio (15 g/kg) and the dew point temperature (70 F). The
problem is worked out in detail below:
First you fill in the air temperature and the RH data that
you are
given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing ratio in your
head. Air that is filled to 50% of its capacity could hold up to
30 g/kg. Half of 30 is 15, that is the mixing ratio. Or you
can substitute into
the relative humidity formula and solve for the mixing ratio.
Finally you imagine cooling the air. The
saturation mixing ratio decreases, the mixing ratio stays constant,
and the relative humidity increases. In this example the RH
reached 100% when the air had cooled to 70 F. That is the dew
point temperature.
We can use
results from humidity problems #1 and #2 to
learn a useful rule.
In the first
example the difference between the air and dew point
temperatures was large (45 F) and the RH was low (20%).
In
the
2nd
problem
the
difference
between
the
air and dew point
temperatures was
smaller (20 F) and the RH was higher (50%). The easiest way to
remember
this
rule is to remember the case where there is no difference between the
air and dew
point temperatures. The RH then would be 100%.
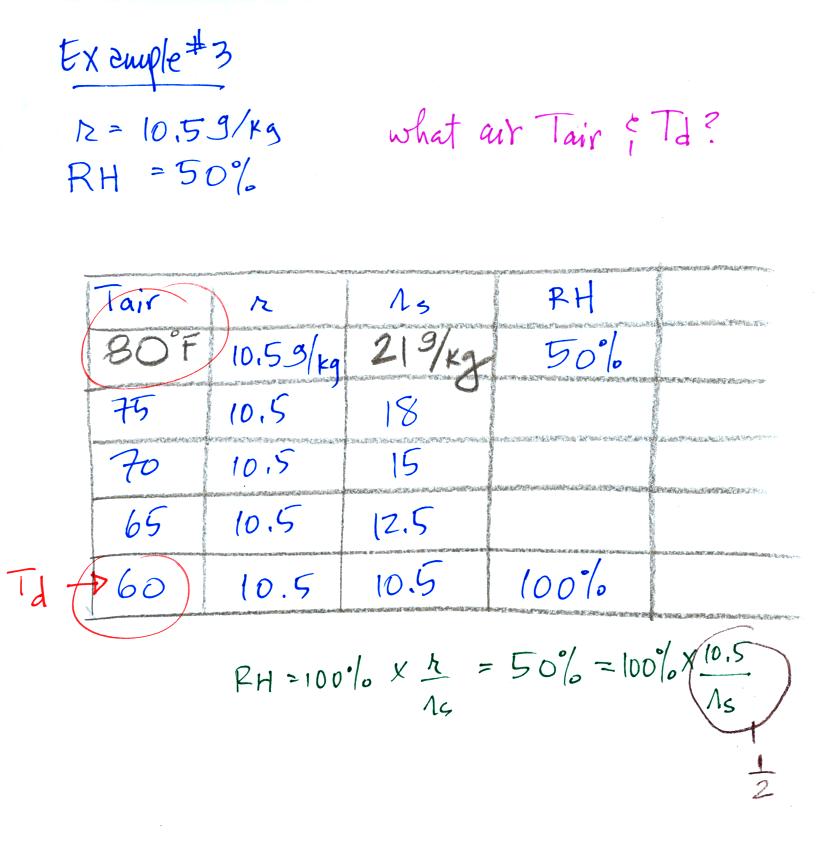
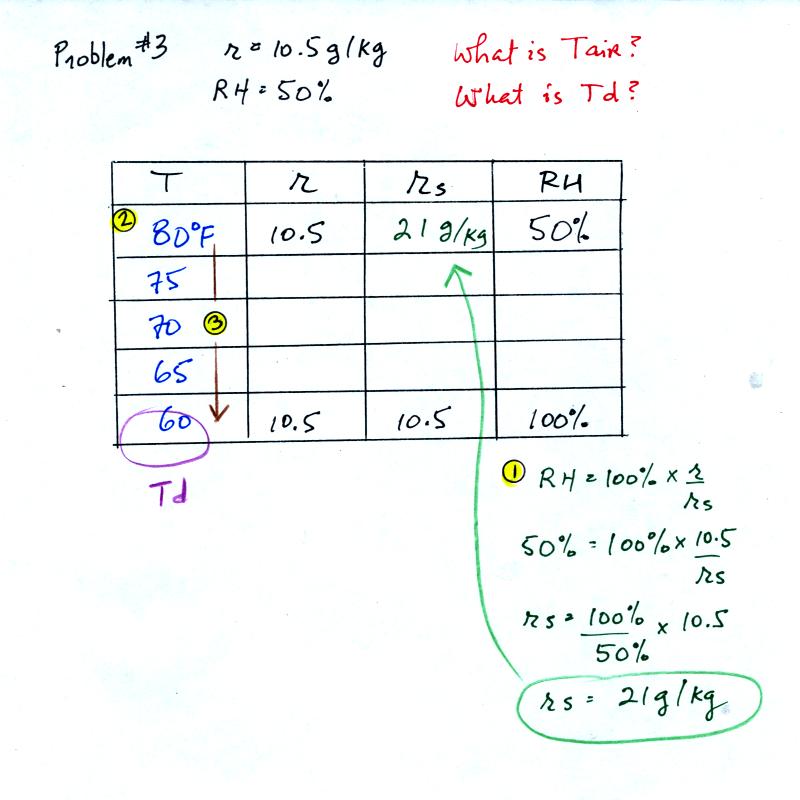
Example 3
You're given the mixing ratio (10.5) and the relative humidity
(50). What are the units (g/kg and %). Here's the play by
play solution to the question
You are given a
mixing ratio
of 10.5 g/kg and a relative humidity of 50%. You need to figure
out the air temperature and the dew point temperature.
(1) The air contains 10.5 g/kg of water vapor, this is 50%,
half, of what the air
could potentially hold. So the air's capacity, the saturation
mixing ratio must be 21 g/kg (you can either do this in your head or
use the RH equation following the steps shown).
(2) Once you know the saturation mixing
ratio you can look up the air temperature in a table (80 F air has a
saturation mixing ratio of 21)
(3) Then you
imagine cooling the air until the RH becomes 100%. This occurs at
60 F. The dew point is 60 F.
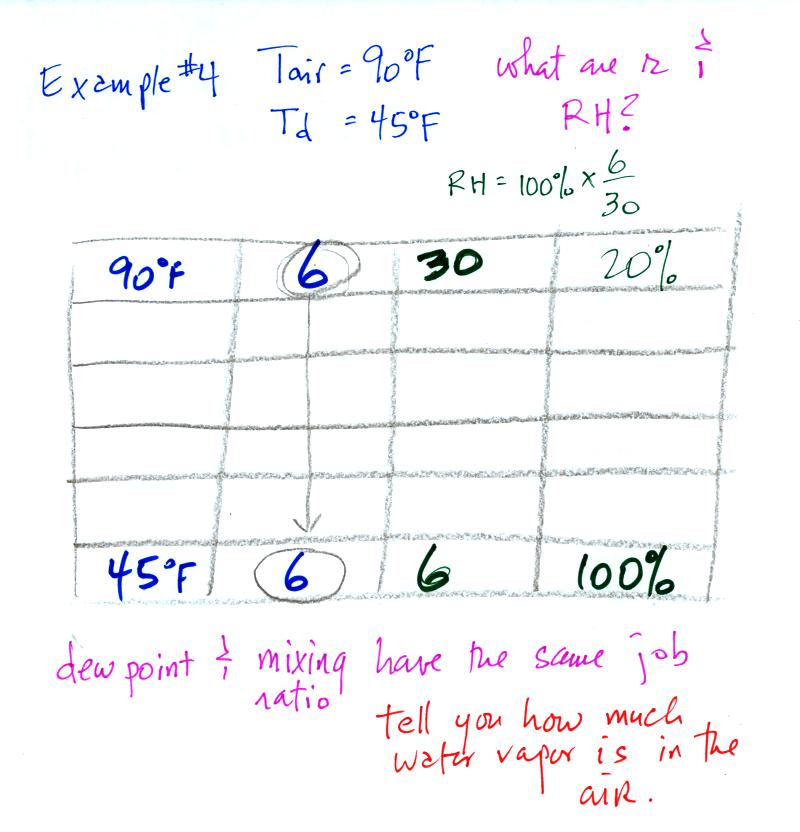
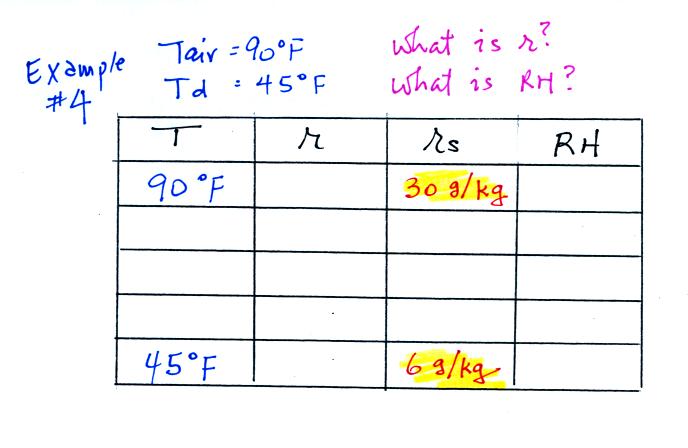
Example 4
probably the most difficult problem of the bunch.
Here's what we did in class, we
were given the air temperature and the dew point temperature. We
were supposed to figure out the mixing ratio and the relative
humidity.
We enter the two temperatures onto a chart and look up the
saturation
mixing ratio for each.
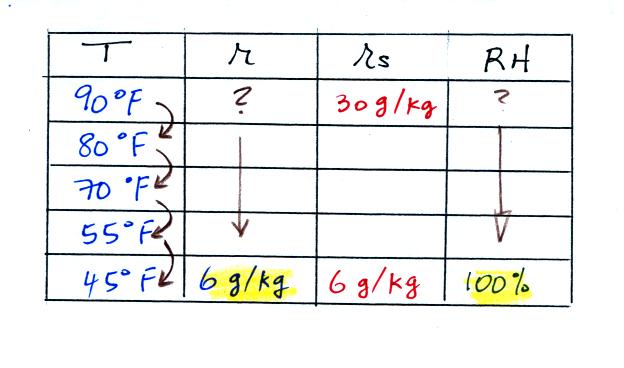
We ignore the fact that we don't know the mixing
ratio. We do know that if we cool the 90 F air to 45 F the RH
will
become
100%. We can set the mixing ratio equal to the value of the
saturation mixing ratio at 45 F, 6 g/kg.
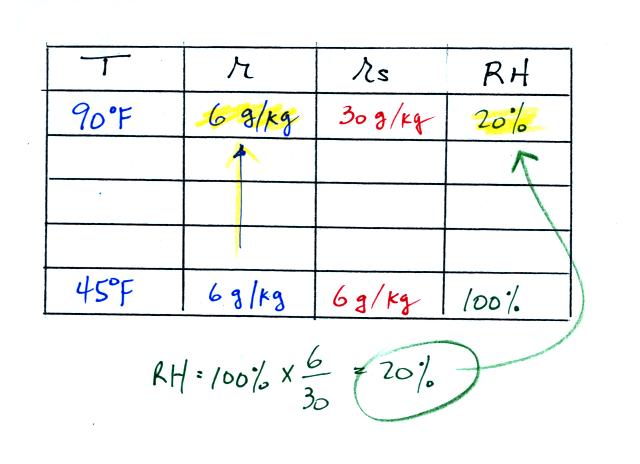
Remember back to the three earlier examples. When we
cooled air
to the the dew point, the mixing ratio didn't change. So the
mixing ratio must have been 6 all along. Once we know the
mixing ratio in the 90 F air it is a simple matter to calculate the
relative humidity, 20%.
Here's a list of some of the important facts and properties of the
4 humidity variables that we have been talking about. This list wasn't
shown in class.
We had
just enough time to start to use what we have learned about humidity
variables (what they tell you about the air and what causes them to
change value) to learn some new things. The figure below is on p.
87 in the photocopied ClassNotes.
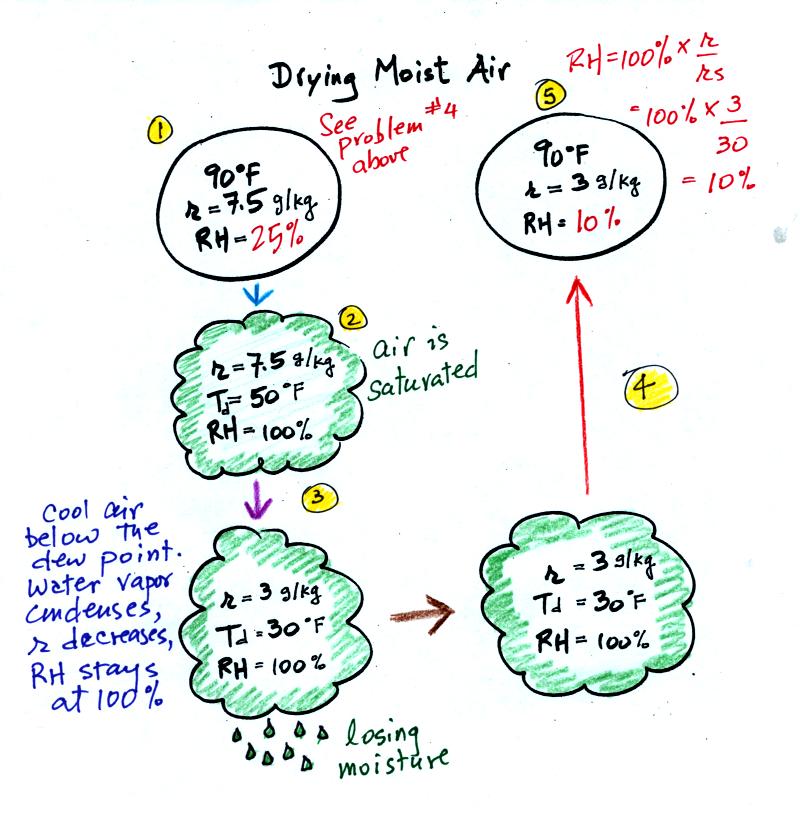
At Point 1 we start with some 90 F air with a relative
humidity of 25%, fairly dry air. Point 2 shows the air being
cooled to the dew
point, that is
where the relative humidity would reach 100% and a cloud would form.
Then the air is cooled below the dew
point, to
30 F. Air that is cooled below the dew point finds itself with
more water vapor than it can contain. The excess moisture must
condense (we will assume it falls out of the air as rain or
snow). When air reaches 30 F it contains 3 g/kg, less than half
the
moisture that it originally did (7.5 g/kg). The air is being
warmed back up to 90 F along Path 4. As it warms the mixing ratio
remains constant. At Point 5, the air
now
has a RH of only 10%.
Drying moist air is very much like wringing moisture from a wet
sponge.
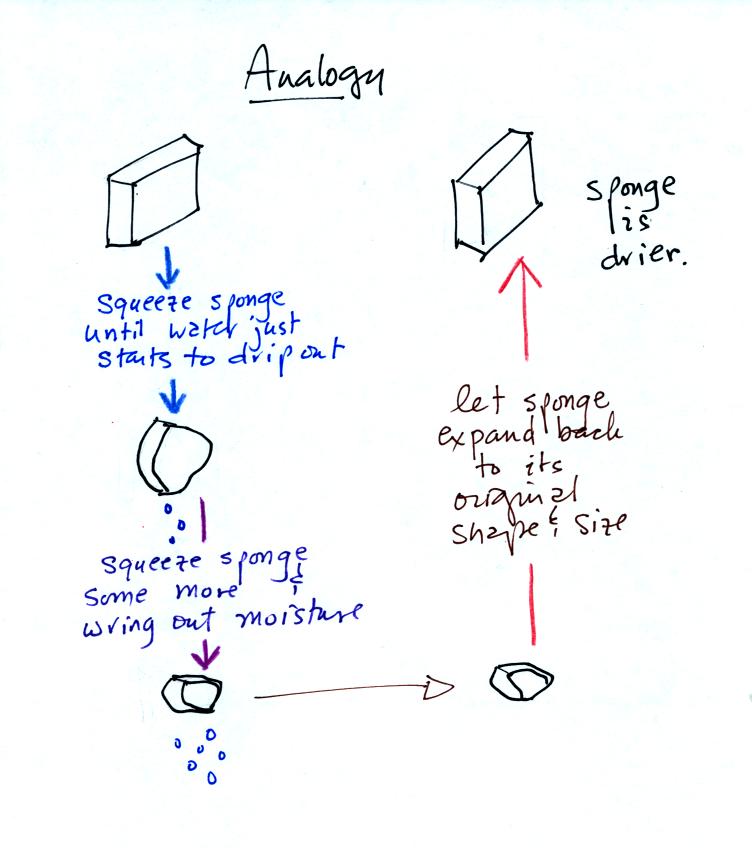
You start to
squeeze the sponge and nothing happens at first (that's like cooling
the air, the mixing ratio stays constant as long as the air doesn't
lose any water vapor). Eventually water will start to drop from
the sponge (with air this is what happens when you reach the dew point
and continue to cool the air below the dew point). Then you let
go of the sponge and let it expand back
to its orignal shape and size (the air warms back to its original
temperature). The sponge (and the air) will be drier than when
you started.
This sort of process ("squeezing" water vapor out of moist air by
cooling the air below its dew point) happens all the time. Here
are a couple of examples (p. 87 again)

The air in an
airplane comes from outside the plane. The air outside the plane
can be very cold (-60 F perhaps) and contains very little water
vapor (even if the -60 F air is saturated it would contain essentially
no water vapor). When brought inside and warmed to a
comfortable
temperature, the RH of the air in the plane will be very close
0%.
Passengers often complain of becoming dehydrated on long airplane
flights. The plane's ventilation system probably adds moisture to
the
air so that it doesn't get that dry.
Here's a midterm grade summary example (numbers in the
example are
class averages)
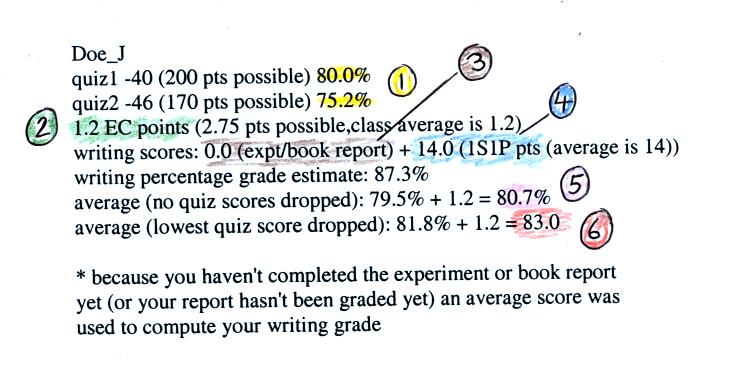
1. You should find your two quiz scores
here. The quiz percentage grades are used to compute your overall
grade; all the quizzes have the same weight.
2. This is the total number of extra credit points
you have earned on the Optional Assignments. The In-class
Optional Assignment from Monday that is being returned today is
included in the total. If you have done all the Optional
Assignments you should have close to the maximum number of points
(unless you elected to receive a
Green Card or 1S1P pts on one of the assignment instead of extra credit
points)
3. If you have turned in an experiment or book report
and it has been graded you should see the score here. If there is
a 0 here, an average grade of
34 out of 40 has been used in the computer to show the effect of the
experiment report on your overall grade.
4. This shows the total number of 1S1P pts you have
earned so far. You should try to earn 45 1S1P pts by the end of
the semester. There will be 2 more 1S1P assignments (with at
least 2 topics per assignment) and another Bonus Assignment or
two. Part of 1S1P Assignment #2 is already online. A due
date hasn't been set yet.
5. This is the average that needs to be 90.0% or
above in order for you to not have to take the final exam.
6. This is the average with the lowest quiz score
dropped. This is the grade that would be used together with your
Final Exam score to determine your overall grade.
The mid term grade estimate gives you an idea of the grade you would
receive at the end of the semester if you continue to perform as you
have so far. It is possible for you to significantly raise your
grade between now and the end of the semester. It is also
possible, of course, for your grade to drop. Please check your
grade summary carefully for errors or omissions.