Thursday Jan. 26, 2012
click here to download today's notes in a more printer friendly format

I was watching a TV show on DVD last Sunday night and heard something called Pinetop's Boogie Woogie.  I wasn't sure there was such a thing but there is.  It's named after Joseph William "Pinetop" Perkins.  Here's a nice version and a little bit longer version both featuring Pinetop Perkins himself.  I played a still longer version from the Silvan Zingg Trio (here's a video featuring Silvan Zingg alone).  There was another catchy piece on the DVD: "Honky Tonk Train Blues" by Meade Lux Lewis.

The In-class Optional Assignment from Tuesday has been graded.  I had them in class but forgot to return them.  I'll have them (together with any papers turned in today) next Tuesday.  In the meantime here are answers to the questions.

The Practice Quiz is Thursday next week (Feb. 2) and the Practice Quiz Study Guide is now available online.  Study guides will also become available about one week before each of the remaining quizzes this semester.  Reviews are scheduled for Monday, Tuesday, and Wednesday afternoon next week (reviews will also precede the remaining quizzes).  The Monday afternoon review is intended for the MWF section of the class and may cover some material you won't see until Tuesday morning but you are welcome to attend.  See the study guide for times and locations of the reviews.

Now that we've learned something about the composition of the atmosphere we will be learning about some of its other physical properties such as temperature, air density, and air pressure.  We'll also be interested in how they change with altitude.

Before we can learn about atmospheric pressure in particular, we need to review the terms mass and weight (the figure above is on p. 23 in the ClassNotes).  Mass is a way of specifying the amount of a particular material and is different than volume or number of atoms or molecules of something.  Grams and kilograms are common units for mass. 

Two bottles, one containing mercury the other an equal volume of water, were passed around class.  Even though the volumes were the same, the masses, weights, and densities were very different.

Other books will define mass as inertia or as resistance to change in motion (this comes from Newton's 2nd law of motion, we'll cover that later in the semester).  The next picture illustrates both definitions. 



A Cadillac and a volkswagen have both stalled in an intersection.  Both cars are made of steel.  The Cadillac is larger and has more steel, more stuff, more mass.  The Cadillac would be much harder to get moving than the VW, it has a larger inertia (it would also be harder to slow down and stop once it is moving).



Weight is a force and depends on both the mass of an object and the strength of gravity.  Weight is something you can feel.  That was another reason for pass around the bottle of mercury, so that you could feel how heavy it was (and it was heavy because it has a lot of mass).  We tend to use weight and mass interchangeably because we spend all our lives on earth where gravity never changes.  On the earth's surface you determine the weight of an object by multiplying the object's mass by g.  As long as you're on the surface of the earth g has a constant value; it's called the gravitational acceleration.

Here are a couple of questions that I asked in class.



We assume that all three objects are here on the earth.


To determine the weight you multiply the mass by the gravitational acceleration.  Since all three objects have the same mass and g is a constant you get the same weight for each object.  That's why we use mass and weight interchangeably on the earth.  Here was a follow up question:

A student responded that the two objects would have different weights if they were on different planets.  That's correct.

Imagine carrying a brick from the earth to the moon.  It would be the same brick in both cases and would have the same mass (note: this is a corrected version of the figure shown in class that showed 1 kg for the mass of the bricks).  The value of the gravitational acceleration on the moon is about 1/6th the value on the earth.  So a brick that weighed 5 pounds on the earth would weigh less than 1 pound on the moon.  The brick would weigh almost 12 pounds on the surface on Jupiter.

Here's a little more information (not covered in class) about what determines the value of the gravitational acceleration (Newton's Law of Universal Gravitation).

Density is the next term we need to look at.



In the first example there is more mass (more dots, which symbolize air molecules) in the right box than in the left box.  Since the two volumes are equal the box at right has higher density.  Equal masses are squeezed into different volumes in the bottom example.  The box with smaller volume has higher density.

Now we're ready to define (and hopefully understand) pressure.  It's a pretty important concept.  A lot of what happens in the atmosphere is caused by pressure differences.  Pressure differences cause wind.  Large pressure difference (such as you might find in a tornado or a hurricane) create powerful and destructive storms.



The air that surrounds the earth has mass.  Gravity pulls downward on the atmosphere giving it weight.  Galileo conducted (in the 1600s) a simple experiment to prove that air has weight.  The experiment wasn't mentioned in class.

Atmospheric pressure depends on, is determined by, the weight of the air overhead.  This is one way, a sort of large scale representation, of understanding air pressure.

Pressure is defined as force divided by area.  In the case of atmospheric pressure the weight of a column of air divided by the area at the bottom of the column (as illustrated above). 

Under normal conditions a 1 inch by 1 inch column of air stretching from sea level to the top of the atmosphere will weigh 14.7 pounds.  Normal atmospheric pressure at sea level is 14.7 pounds per square inch (psi, the units you use when you fill up your car or bike tires with air).

The iron bar sketched below was passed around class today.  You were supposed to estimate it's weight.




It also weighs 14.7 pounds.  When you stand the bar on end, the pressure at the bottom would be 14.7 psi.


So the weight of a 1" x 1" steel bar 52 inches long is the same as a 1" x 1" column of air that extends from sea level to the top of the atmosphere 100 or 200 miles (or more) high.  The pressure at the bottom of both would be 14.7 psi.

Psi are perfectly good pressure units, but they aren't the ones that most meteorologists use.


Typical sea level pressure is 14.7 psi or about 1000 millibars (the units used by meterologists and the units that we will use in this class most of the time) or about 30 inches of mercury (refers to the reading on a mercury barometer, we'll cover mercury barometers on Friday, they're used to measure pressure).  Milli means 1/1000 th.  So 1000 millibars is the same as 1 bar.  You sometimes see typical sea level pressure written as 1 atmosphere.

Mercury (13.6 grams/cm3)  is denser than steel ( about 7.9 grams/cm3 ) so it would only take about a 30 inch tall column of mercury to produce atmospheric presure.

Each of these columns would weigh 14.7 pounds.  The pressure at the base of each would be the same.

You never know whether something you learn in NATS 101 (or ATMO 170A1 as it's now called) will turn up.  I lived and worked for a short time in France (a very enjoyable and interesting period in my life).  Here's a picture of a car I owned when I was there (this one is in mint condition, mine was in far worse shape and cost less than $200)



It's a Peugeot 404.  After buying it I took it to the service station to fill it with gas and to check the air pressure in the tires.  I was a little confused by the air compressor though, the scale only ran from 0 to 3.  I'm used to putting 30 psi or so in my car tires (about 90 psi in my bike tires).  After staring at the scale for a while I finally realized the numbers were pressures in "bars" not "psi".  Since 14.7 psi is equivalent to 1 bar, 30 psi would be about 2 bars.  So I filled up all the tires and carefully drove off (one thing I learned you have to watch out for in France is the "Priority to the right" rule).

You can learn a lot about pressure from bricks. 

For example the photo below (taken in my messy office) shows two of the bricks from class.  One is sitting flat, the other is sitting on its end.  Each brick weighs about 5 pounds.  Would the pressure at the base of each brick be the same or different in this kind of situation? 



Pressure is determined by (depends on) weight so you might think the pressures would be equal.  But pressure is weight divided by area.  In this case the weights are the same but the areas are different.  In the situation at left the 5 pounds must be divided by an area of about 4 inches by 8 inches = 32 inches.  That works out to be about 0.15 psi.  In the other case the 5 pounds should be divided by a smaller area, 4 inches by 2 inches = 8 inches.  That's a pressure of 0.6 psi, 4 times higher.  Notice also these pressures are much less the 14.7 psi sea level atmospheric pressure.

The main reason I brought the bricks was so that you could understand what happens to pressure with increasing altitude.  Here's a drawing of the 5 bricks stacked on top of each other.

At the bottom of the pile you would measure a weight of 25 pounds (if you wanted to find the pressure you'd divide 25 lbs by the 32 square inch area on the bottom of the brick).  If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks that are still above.  The pressure would be less.  Weight and pressure will decrease as you move up the pile.

The atmosphere is really no different.  Pressure at any level is determined by the weight of the air still overhead.  Pressure decreases with increasing altitude because there is less and less air remaining overhead.  The figure below is a more carefully drawn version of what was done in class.



At sea level altitude, at Point 1, the pressure is normally about 1000 mb.  That is determined by the weight of all (100%) of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of central Tucson is a little lower than that around 2500 feet).  At 3000 ft. about 10% of the air is below, 90% is still overhead.  It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson.  If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb. 

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3) and 70% of the atmosphere is overhead..

Pressure decreases rapidly with increasing altitude.  We will find that pressure changes more slowly if you move horizontally.  Pressure changes about 1 mb for every 10 meters of elevation change.  Pressure changes much more slowly normally if you move horizontally: about 1 mb in 100 km.  Still the small horizontal changes are what cause the wind to blow and what cause storms to form.

Point 4 shows a submarine at a depth of about 30 ft. or so.  The pressure there is determined by the weight of the air and the weight of the water overhead.  Water is much denser and much heavier than air.  At 30 ft., the pressure is already twice what it would be at the surface of the ocean (2000 mb instead of 1000 mb).


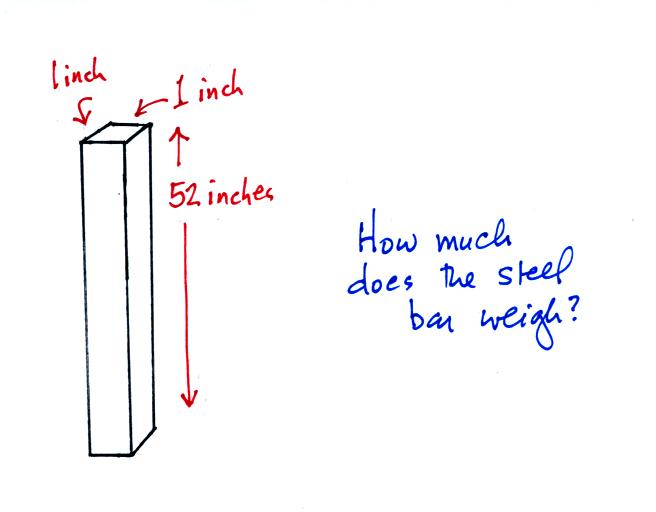
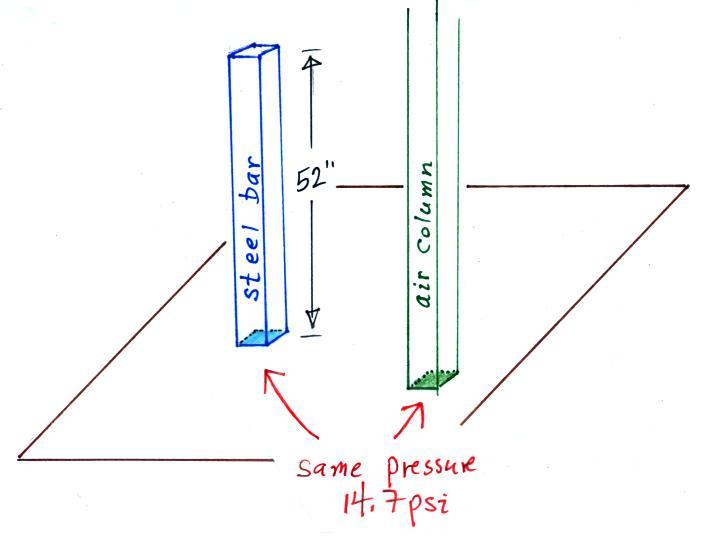
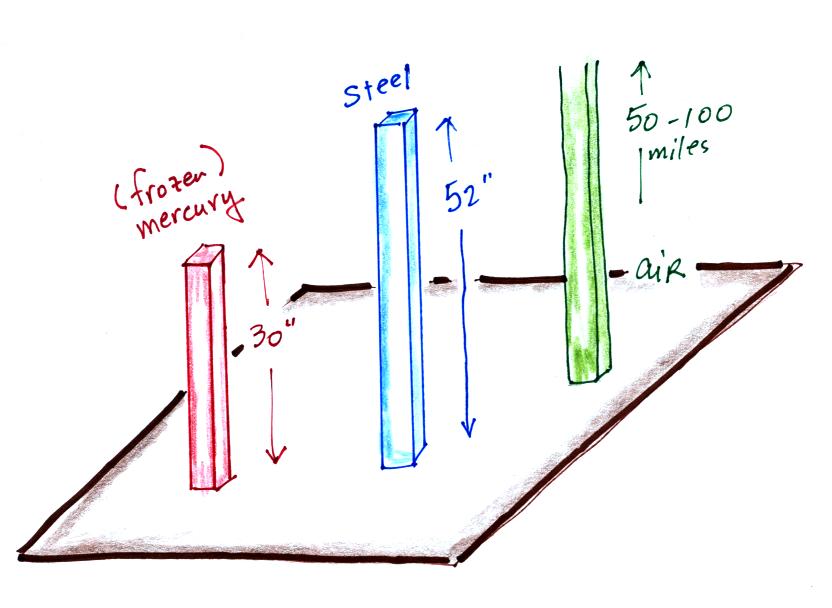
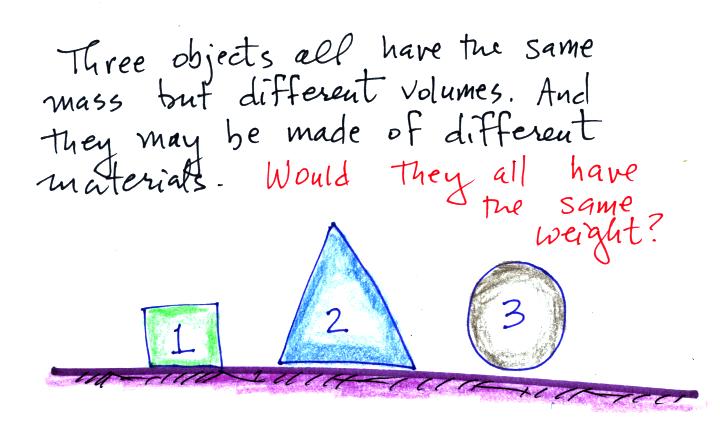The next bunch of material tries to explain how a mercury barometer works.  A mercury barometer is used to measure atmospheric pressure and is really just a balance that can be used to weigh the atmosphere.  You'll find a messier version of what follows on p. 29 in the photocopied Class Notes. 






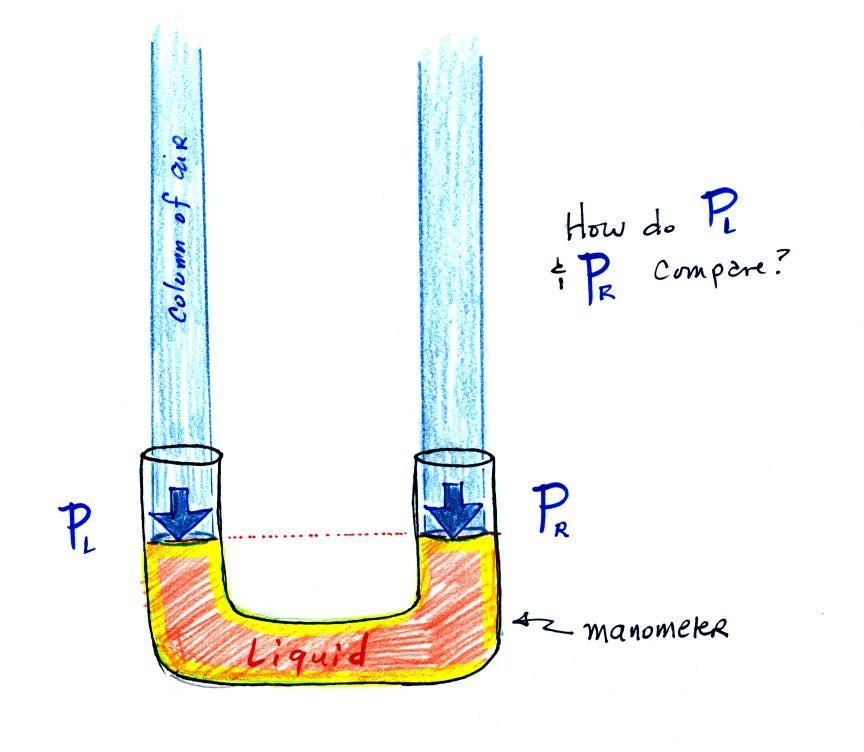
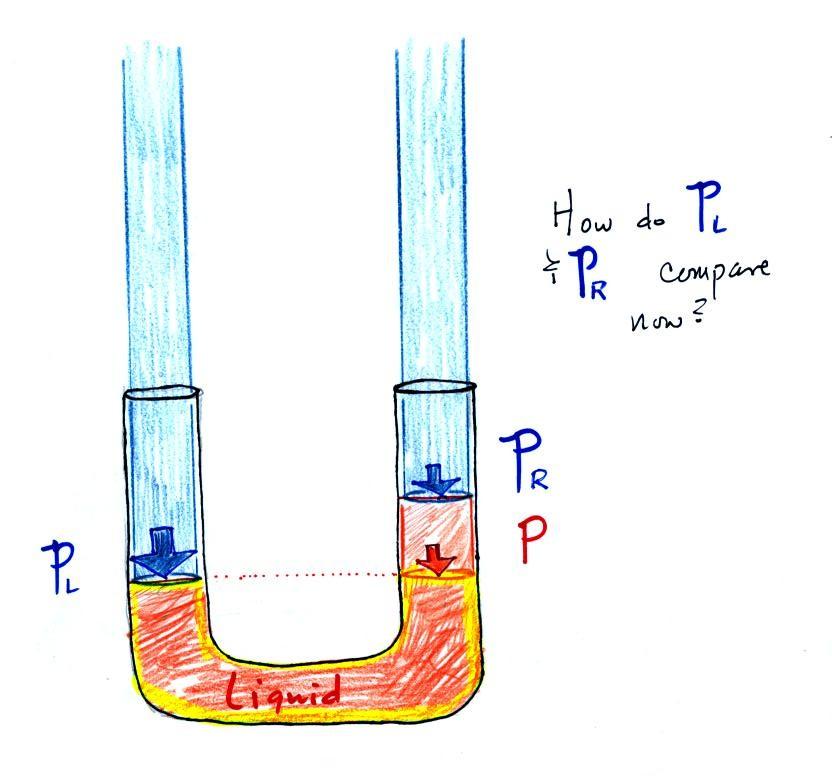
The instrument in the left figure above ( a u-shaped glass tube filled with a liquid of some kind) is actually called a manometer and can be used to measure pressure difference.  The two ends of the tube are open so that air can get inside and air pressure can press on the liquid.  Given that the liquid levels on the two sides of  the manometer are equal, what could you about PL and PR?

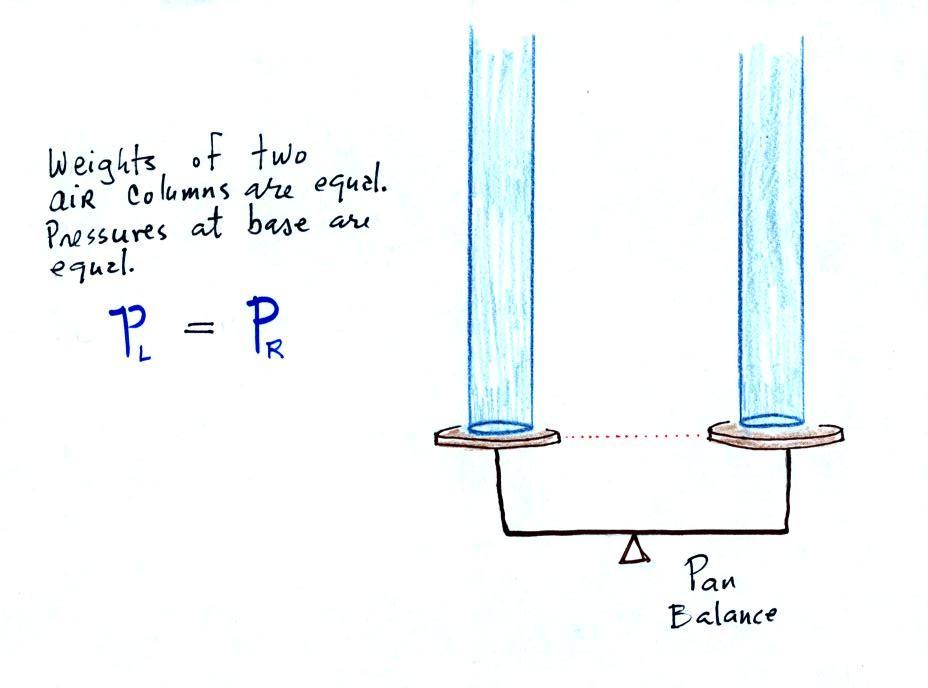
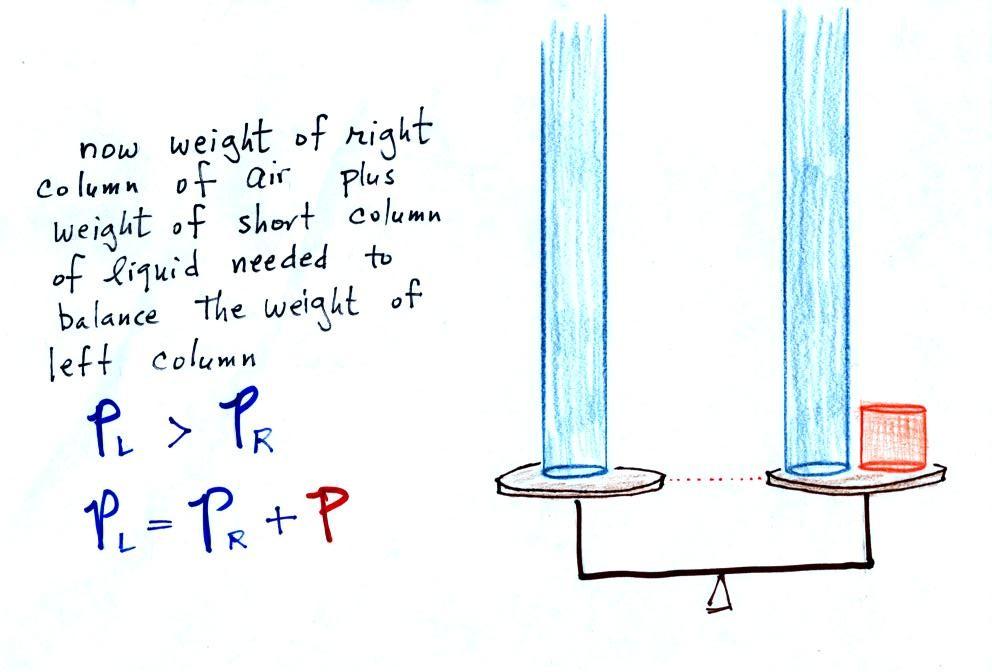
The liquid can slosh back and forth just like the pans on a balance can move up and down.  A manometer really behaves just like a pan balance (pictured at right) or a teeter totter (seesaw).  Because the two pans are in balance, the two columns of air have the same weight.   PL and PR are equal (but note that you don't really know what either pressure is, just that they are equal).


Now the situation is a little different, the liquid levels are no longer equal.  You probably realize that the air pressure on the left, PL, is a little higher than the air pressure on the right, PR.  PL is now being balanced by PR + P acting together.  P is the pressure produced by the weight of the extra fluid on the right hand side of the manometer (the fluid that lies above the dotted line).  The height of the column of extra liquid provides a measure of the difference between PL and PR.

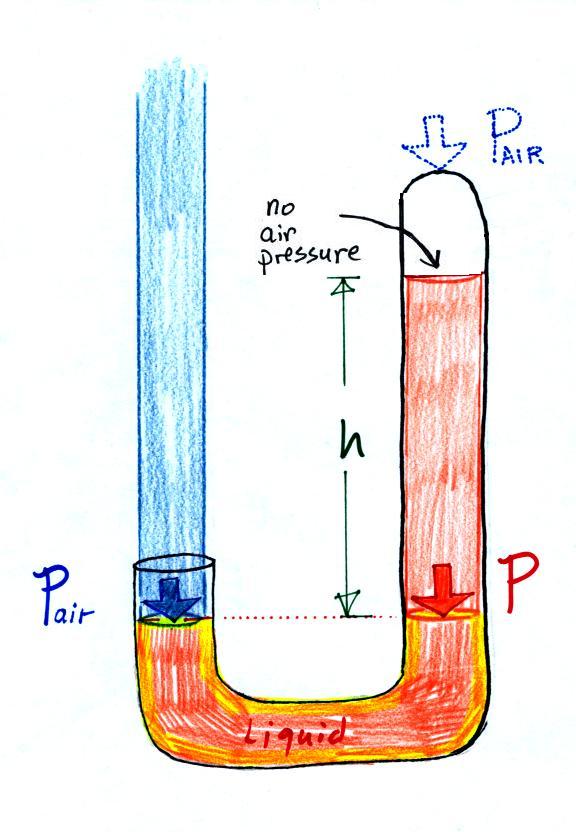
Next we will just go and close off the right hand side of the manometer.



Air pressure can't get into the right tube any more.  Now at the level of the dotted line the balance is between Pair and P (pressure by the extra liquid on the right).  If Pair changes, the height of the right column, h,  will change.  You now have a barometer, an instrument that can measure and monitor the atmospheric pressure.

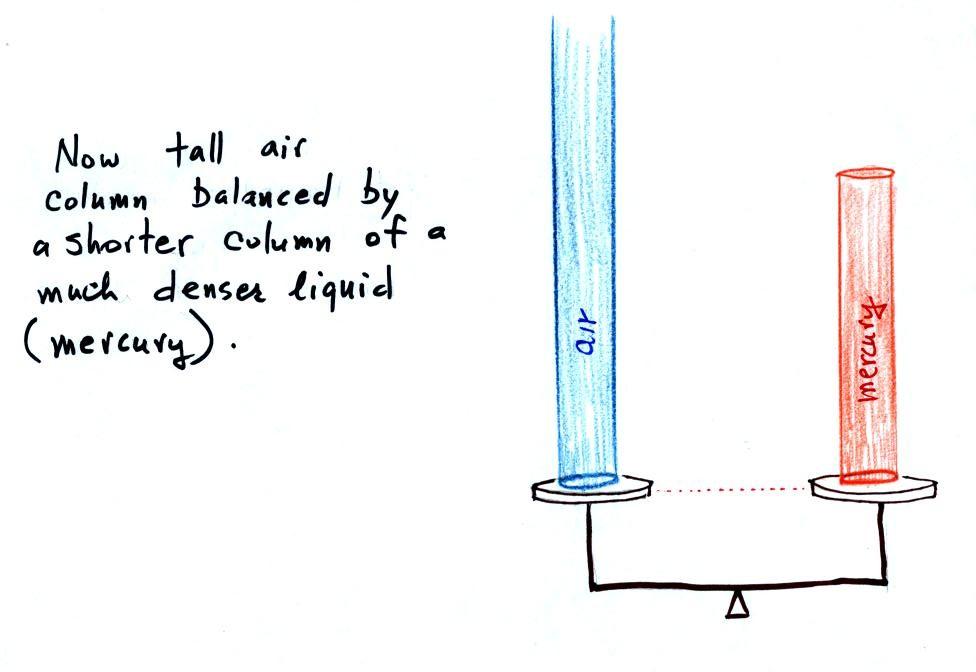
Barometers like this are usually filled with mercury.  Mercury is a liquid.  You need a liquid that can slosh back and forth in response to changes in air pressure.  Mercury is also very dense which means the barometer won't need to be as tall as if you used something like water.  A water barometer would need to be over 30 feet tall.  With mercury you will need only a 30 inch tall column to balance the weight of the atmosphere at sea level under normal conditions (remember the 30 inches of mercury pressure units mentioned earlier).  Mercury also has a low rate of evaporation so you don't have much mercury gas at the top of the right tube (there's some gas, it doesn't produce much pressure, but it would poison you if you were to start to breath it).



Here is a more conventional barometer design.  The bowl of mercury is usually covered in such a way that it can sense changes in pressure but is sealed to keep poisonous mercury vapor from filling a room.



Average sea level atmospheric pressure is about 1000 mb.  The figure above (p. 30 in the photocopied Class Notes) gives 1013.25 mb but 1000 mb is close enough in this class.  The actual pressure can be higher or lower than this average value and usually falls between 950 mb and 1050 mb. 

The figure also includes record high and low pressure values.  Record high sea level pressure values occur during cold weather.  The TV weather forecast will often associate hot weather with high pressure.  They are generally referring to upper level high pressure (high pressure at some level above the ground) rather than surface pressure.

Most of the record low pressure values have all been set by intense hurricanes (the extreme low pressure is the reason these storms are so intense).  Hurricane Wilma in 2005 set a new record low sea level pressure reading for the Atlantic, 882 mb.  Hurricane Katrina had a pressure of 902 mb.  The following table lists some of the information on hurricane strength from p. 146a in the photocopied ClassNotes.  3 of the 10 strongest N. Atlantic hurricanes occurred in 2005.


Most Intense North Atlantic Hurricanes
 Most Intense Hurricanes
to hit the US Mainland
Wilma (2005) 882 mb
Gilbert (1988) 888 mb
1935 Labor Day 892 mb
Rita (2005) 895 mb
Allen (1980) 899
Katrina (2005) 902
 1935 Labor Day 892 mb
Camille (1969) 909 mb
Katrina (2005) 920 mb
Andrew (1992) 922 mb
1886 Indianola (Tx) 925 mb

Note that a new all time record low sea level pressure was measured in 2003 inside a strong tornado in Manchester, South Dakota (F4 refers to the Fujita scale rating, F5 is the highest level on the scale).  This is very difficult (and potentially dangerous thing) to do.  Not only must the instruments be built to survive a tornado but they must also be placed on the ground ahead of an approaching tornado and the tornado must then pass over the instruments.

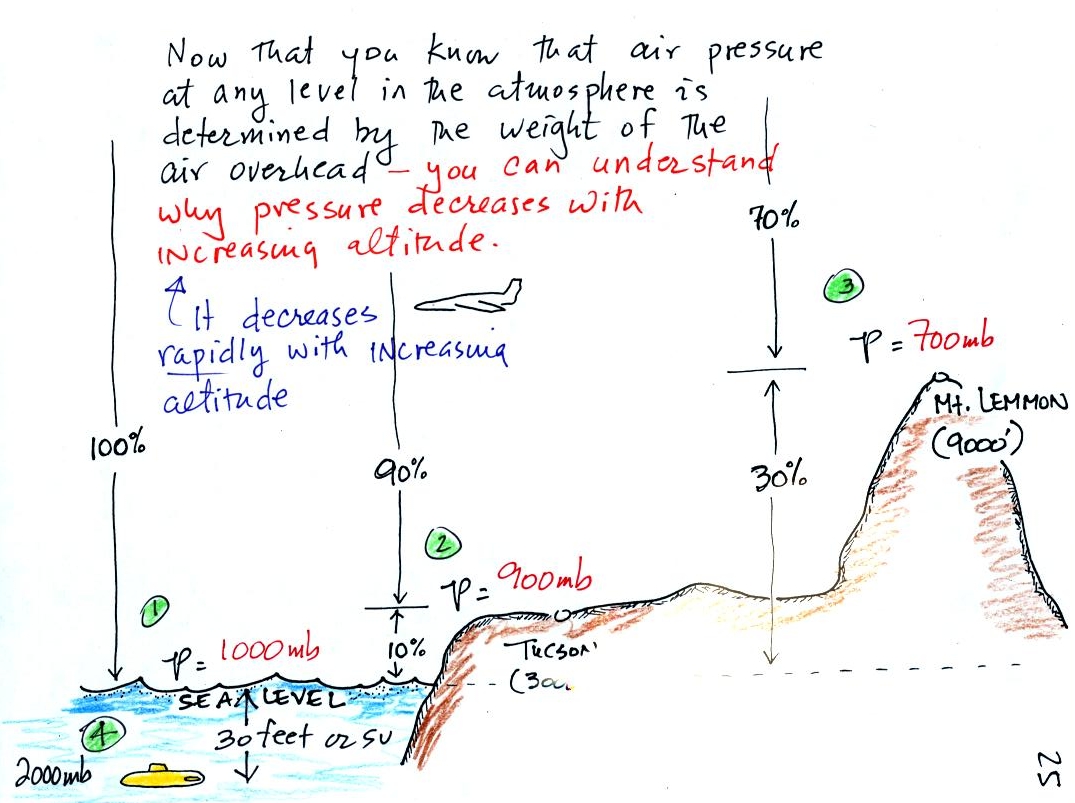
We saved a more difficult concept for last.  This next figure explains the rate of pressure change as you move or down in the atmosphere depends on air density.  In particular air pressure will decrease more quickly when you move upward through high density air than if you move upward through low density air.


1. The rate of pressure decrease with increasing altitude is greatest in Layer A.  To determine the rate of pressure decrease you divide the pressure change (100 mb for both layers) by the distance over which that change occurs.  The 100 mb change takes place in a shorter distance in Layer A than in Layer B.  Layer A has the highest rate of pressure decrease with increasing altitude.

2.  There is a 100 mb drop in pressure in both air layers.  Pressure depends on the weight of the air overhead.  As you move upward in the atmosphere you remove air that was above and put it below you.  If the pressure change is the same in both layers, you must have moved the same weight of air in both cases.  Both layers must have the same amount (the same mass) of air.

3.  Density is mass divided by volume.  The air in the Layer A is denser than the air in Layer B.  The same amount (mass) of air is squeezed into a thinner layer, a smaller volume, in the left layer.  This results in higher density air.

So both the most rapid rate of pressure decrease with altitude and the densest air are found in Layer A.

The fact that the rate of pressure decrease with increasing altitude depends on air density is a fairly subtle but important concept.  This concept will come up 2 or 3 more times later in the semester.  For example, we will need this concept to explain why hurricanes can intensify and get as strong as they do.