Monday Feb. 25, 2013
click here to download
today's notes in a more printer friendly format
You heard "Lover's
Carvings" from Bibio before class. It was something I
heard watching TV over the weekend. I was too busy playing
with my new laser pointers to spend much time thinking about music
for today.
The Experiment #2 reports were collected today. It will take
a week or so to get them all graded so you should expect to get
them back sometime next week.
The Upper Level Chart Optional Assignment has been graded.
If you missed 3 pts or less you got a Green Card. Everyone
got extra credit (0.5 pts). I hope to have the CO2
reports graded by Wednesday (Friday at the
latest). I'm also working still on the Surface Weather Map
Analysis.
I am now the owner of a red, green, and purplish blue laser
pointer. They're bright and you can see them on the screen
even when the projector is on. I projected the left figure
below onto one of the projector screens and pointed each of the
laser pointers so that its light would fill the proper circle
below (purple-blue in the 405 nm circle, green in the 532 nm
circle, and red in the 650 nm circle). Note
nanometers (nm) are billionths of a meter and is just another type
of unit that you can use for wavelength; 405 nm is the same as
0.405 µm.
The picture at right below (from Wikipedia)
gives you a pretty good idea of what the light from each laser
pointer looked like.
What I really wanted to do was to orient the laser pointers so
that the spots of light would fall on top of each other. We
should get something that looks white because mixing all the
colors of visible light together produces white light. The
resulting spot of light was pretty small but did look whitish (one
problem is that the intensities of the laser pointers are
different).
Here's another illustration of how mixing red, green, and blue
light produces white light (again from
Wikipedia)
A good question came up at the end of Friday's class. "If
white light is a mixture of all the colors, why, when you mix
together a bunch of different colors of paint, does the mixture
turn black"?
It might be easiest to explain (and demonstrate) with
filters.
A red filter will only let red light through (the other colors
are absorbed), a green filter transmits only green light.
When you put the red and green filters back to back nothing gets
through.
Paint is similar except it involves reflection instead of
transmission (absorption is involved in both cases).
The pigments in green paint absorb everything except
for green. Green is reflected.
Red paint absorbs everything except for red.
When you paint an object with both red and green (and all the
other colors just to play it safe) everything is
absorbed. No light is reflected and the object appears
black. For the bottom figure I took the 7 colored
pencils used to draw the 7 rays of colored light and colored
in the square. The result is not exactly black but it is
headed in that direction. Grab some colored pencils and
try it yourself.
We spent most of the rest of the
class learning about some rules governing the emission of
electromagnetic radiation. Here they are:
1.
Everything
warmer than 0 K will emit EM radiation. Everything in the
classroom: the people, the furniture, the walls and the floor,
even the air, are emitting EM radiation. Often this
radiation will be invisible so that we can't see it and weak
enough that we can't feel it (or perhaps because it is always
there we've grown accustomed to it and ignore it). Both
the amount and kind (wavelength) of the emitted radiation depend
on the object's temperature. In the classroom most
everything has a temperature of around 300 K and we will see
that means everything is emitting infrared (IR) radiation with a
wavelength of about 10µm.
2.
The second
rule allows you to determine the amount of EM radiation (radiant
energy) an object will emit. Don't worry about the units
(though they're given in the figure below), you can think of
this as amount, or rate, or intensity. Don't worry about σ (the Greek character rho) either, it is just a
constant. The amount depends on
temperature to the fourth power. If the temperature of an
object doubles the amount of energy emitted will increase by a
factor of 2 to the 4th power (that's 2 x 2 x 2 x 2 = 16).
A hot object just doesn't emit a little more energy than a cold
object it emits a lot more energy than a cold object. This
is illustrated in the following figure:
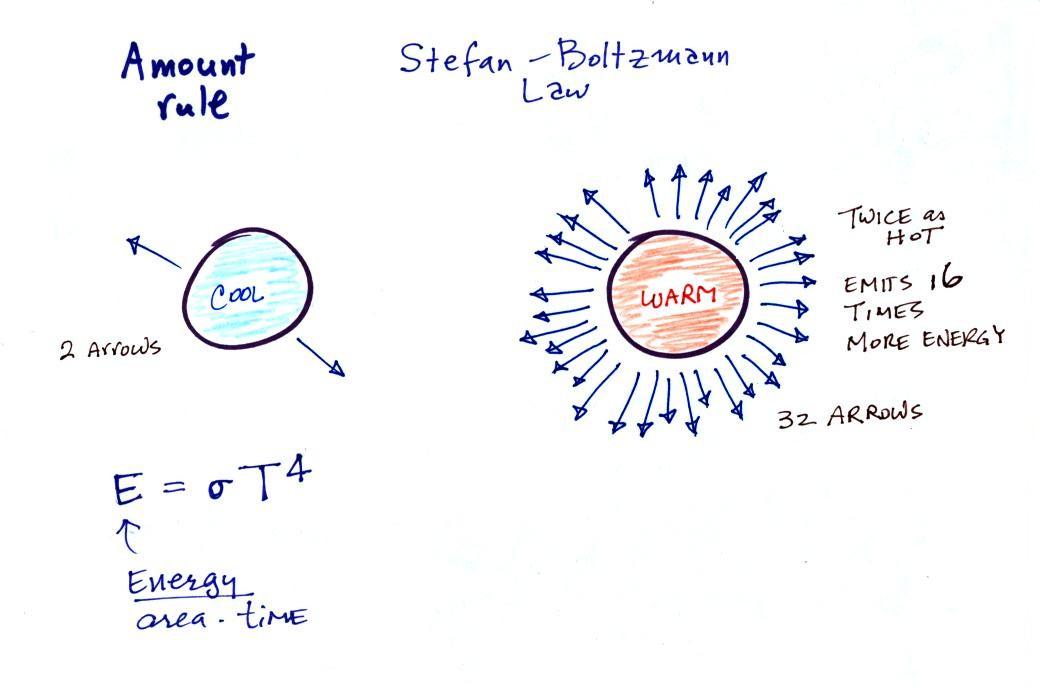
The cool object is emitting 2
arrows worth of energy. This could be the earth at 300
K. The warmer object is 2 times warmer, the earth heated
to 600 K. The earth then would emit 32 arrows (16 times
more energy).
The earth has a temperature of 300 K. The sun is 20
times hotter (6000 K). Every square foot of the sun's
surface will emit 204 (160,000)
times more energy than a square foot of the earth's surface.
3.
The third
rule tells you something about the kind of radiation emitted by
an object. We will see that objects usually emit radiation
at many different wavelengths but not in equal amounts.
But, objects emit more of one particular wavelength than any of
the others. This is called λmax
("lambda max", lambda is the greek character used to represent
wavelength) and is the wavelength of maximum emission. The
third rule allows you to calculate λmax.
The tendency for warm objects to emit radiation at shorter
wavelengths is shown below.
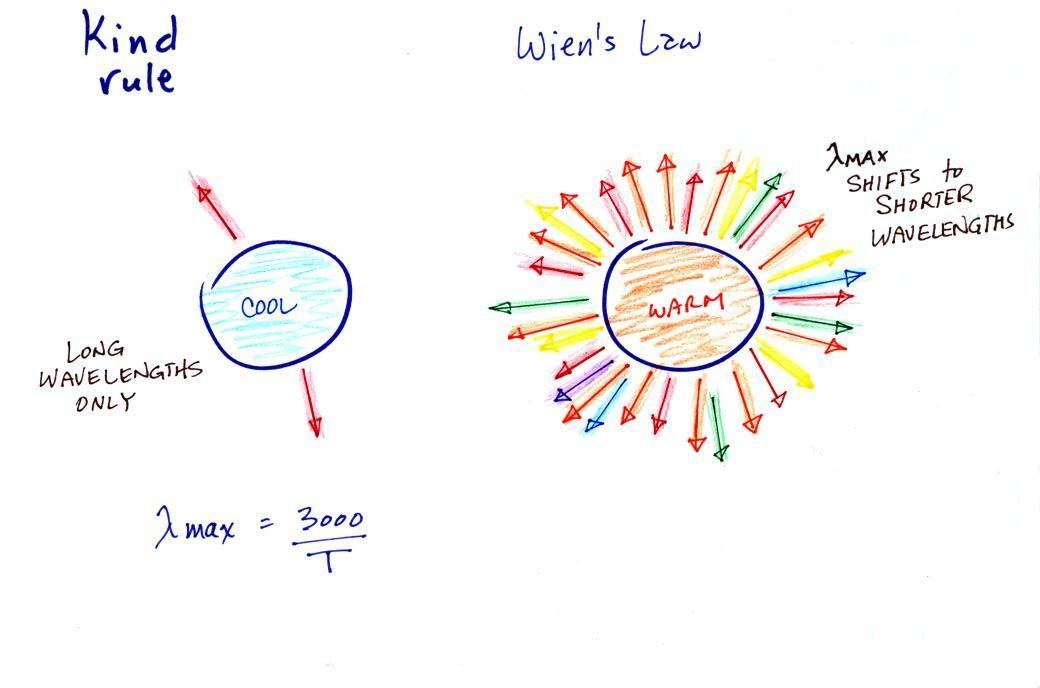
The cool object is probably
emitting infrared light (that would be the case for the earth at
300 K) so the 2 arrows of energy are colored red. The
warmer object will also emit IR light but also shorter
wavelengths such as yellow, green, blue, and violet (maybe even
some UV if it's
hot enough). Remember when
you start mixing different colors of visible light you get
something that starts to look white.
The graphs at the bottom of p. 65 in the photocopied
ClassNotes also help
to illustrate and explain the Stefan-Boltzmann law
and Wien's laws. We're really beating this topic to death
and we're not done yet.
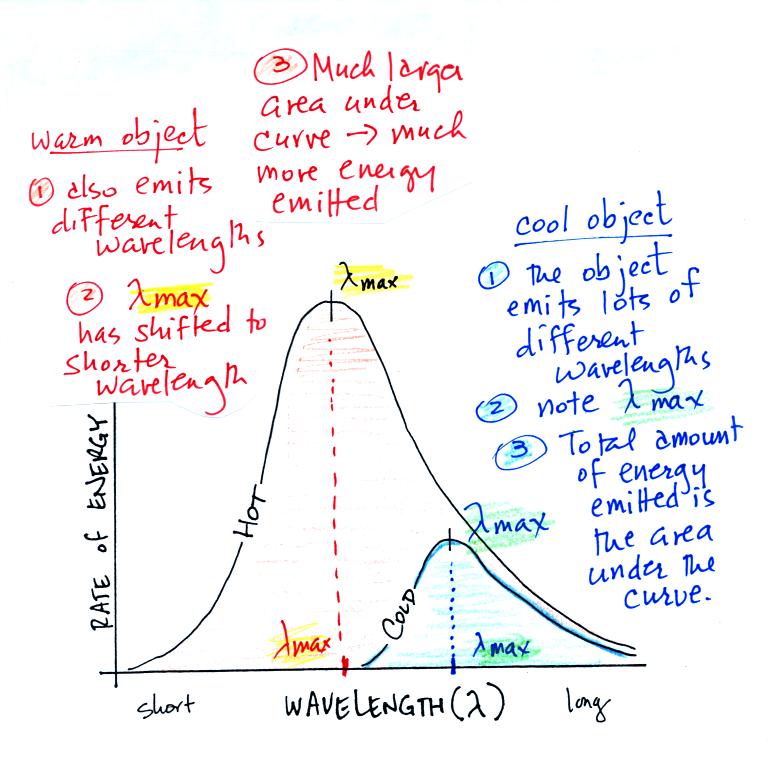
1.
Notice first
that both and warm and the cold objects emit radiation over a
range of wavelengths (the curves above are like quiz scores, not
everyone gets the same score, there is a distribution of
grades). The warm object emits all the wavelengths the
cooler object does plus lots of additional shorter wavelengths.
2.
The peak of
each curve is λmax. Note
that
λmax has shifted
toward shorter wavelengths for the warmer object. This is
Wien's law in action. The warmer object is emitting lots
of types of short wavelength radiation that the colder object
doesn't emit.
3.
The area
under the warm object curve is much bigger than the area under
the cold object curve. The area under the curve is a
measure of the total radiant energy emitted by the object.
This illustrates the fact that the warmer object emits a lot
more radiant energy than the colder object.
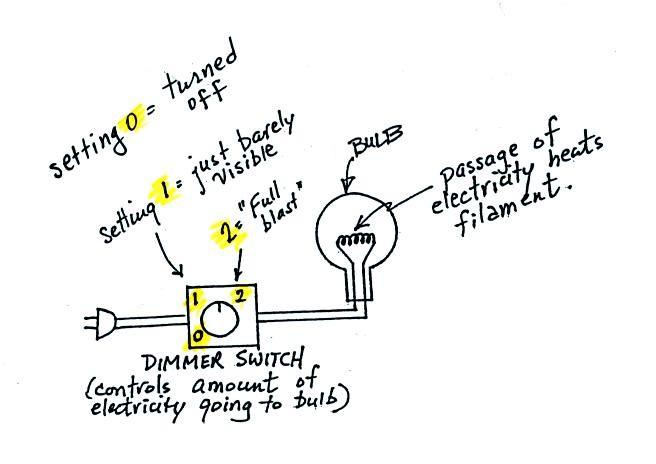
And next a demonstration of the
Stefan-Boltzmann and Wien's Laws. It consisted of an
ordinary 200 W tungsten bulb is connected to a dimmer switch
(see p. 66 in the photocopied ClassNotes). We'll be
looking at the EM radiation emitted by the bulb filament.
The graph at the bottom of p. 66 has been split up into 3
parts and redrawn for improved clarity.
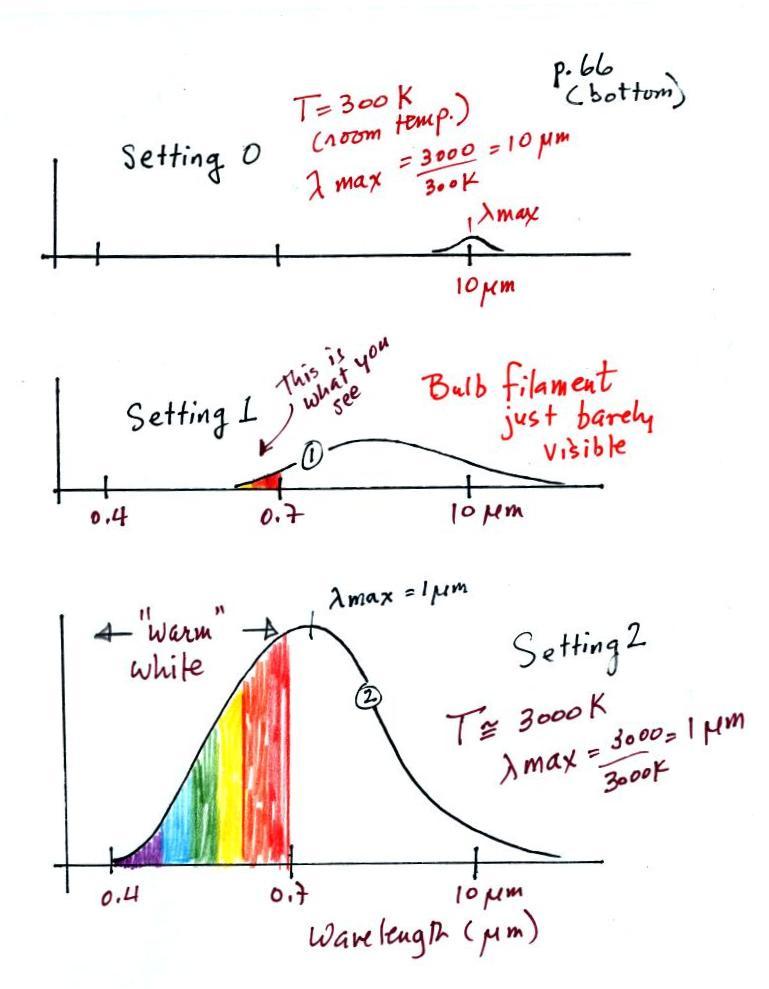
We start with the bulb turned off (Setting 0). The
filament will be at room temperature which we will assume is
around 300 K (remember that is a reasonable and easy to
remember value for the average temperature of the earth's
surface). The bulb will be emitting radiation, it's
shown on the top graph above. The radiation is very weak
so we can't feel it. The wavelength of peak
emission is 10 micrometers which is long
wavelength, far IR radiation so we can't see it.
Next we use the dimmer switch to just barely turn the bulb
on (the temperature of the filament is now about 900 K).
The bulb wasn't very bright at all and had an orange
color. This is curve 1, the middle figure. Note
the far left end of the emission curve has moved left of the
0.7 micrometer mark - into the visible portion of the
spectrum. That is what you were able to see, just the
small fraction of the radiation emitted by the bulb that is
visible light (but just long wavelength red and orange
light). Most of the radiation emitted by the bulb is to
the right of the 0.7 micrometer mark and is invisible IR
radiation (it is strong enough now that you could feel it if
you put your hand next to the bulb).
Finally we turn on the bulb completely (it was a 200 Watt
bulb so it got pretty bright). The filament temperature
is now about 3000K. The bulb is emitting a lot more
visible light, all the colors, though not all in equal
amounts. The mixture of the colors produces a "warm
white" light. It is warm because it is a mixture that
contains a lot more red, orange, and yellow than blue, green,
and violet light. It is interesting that most of the
radiation emitted by the bulb is still in the IR portion of
the spectrum (lambda max is 1 micrometer). This is
invisible light. A tungsten bulb like this is not
especially efficient, at least not as a source of visible
light.
You were able to use one of the diffraction gratings handed
out in class to separate the white light produced by the bulb
into its separate colors.
When you looked at the bright white bulb filament through
one of the diffraction gratings the colors were smeared out to
the right and left as shown at left below.
Some of the gratings handed
out in class behaved a little differently and spread out the
colors horizontally, vertically, and diagonally (right sketch
above)
Here are the rules for the amount and kind (wavelength of
peak emission) of radiation emitted by an object.
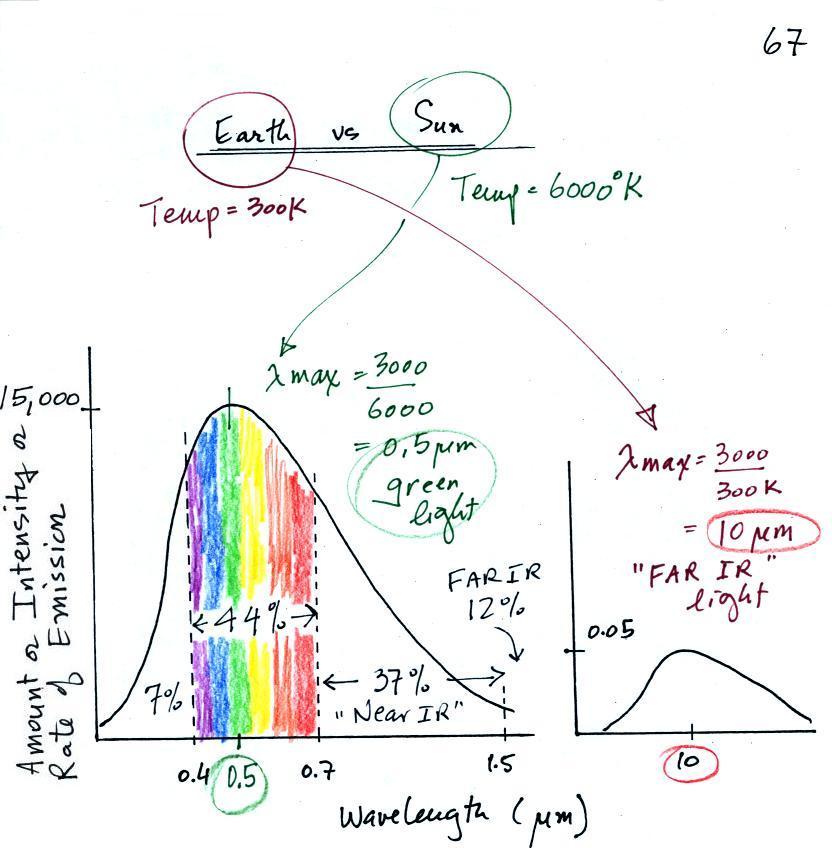
Let's look at the light emitted by the sun and the earth.
The curve on the left is for the sun. We have used
Wien's law and a temperature of 6000 K to calculate λmax
and got 0.5 micrometers. This is green light; the sun
emits more green light than any other kind of light. The
sun doesn't appear green because it is also emitting lesser
amounts of violet, blue, yellow, orange, and red - together
this mix of colors appears white. 44% of the radiation
emitted by the sun is visible light, Very nearly half of
sunlight (49%) is IR light (37% near IR + 12% far IR).
7% of sunlight is ultraviolet light. More than half of
the light emitted by the sun (the IR and UV light) is
invisible.
100% of the light emitted by the earth (temperature = 300 K)
is invisible IR light. The wavelength of peak emission
for the earth is 10 micrometers.
Because the sun (surface of the sun) is 20 times
hotter than the earth the sun's surface emits energy at a much
higher rate than the earth. Note the
vertical scale on the earth curve is different than on the sun
graph. If both the earth and sun were plotted with the
same vertical scale, the earth curve would be too small to be
seen.
In the demonstration in class last Friday we also learned
that ordinary tungsten bulbs (incandescent bulbs) produce a
lot of wasted energy. This is because they emit a lot of
invisible infrared light that doesn't light up a room (it will
warm up a room but there are better ways of doing that).
The light that they do produce is a warm white color (tungsten
bulbs emit lots of orange, red, and yellow light and not much
blue, green or violet).
Energy efficient compact fluorescent lamps (CFLs) are being
touted as an ecological alternative to tungsten bulbs because
they use substantially less electricity, don't emit a
lot of wasted infrared light, and also last longer. CFLs
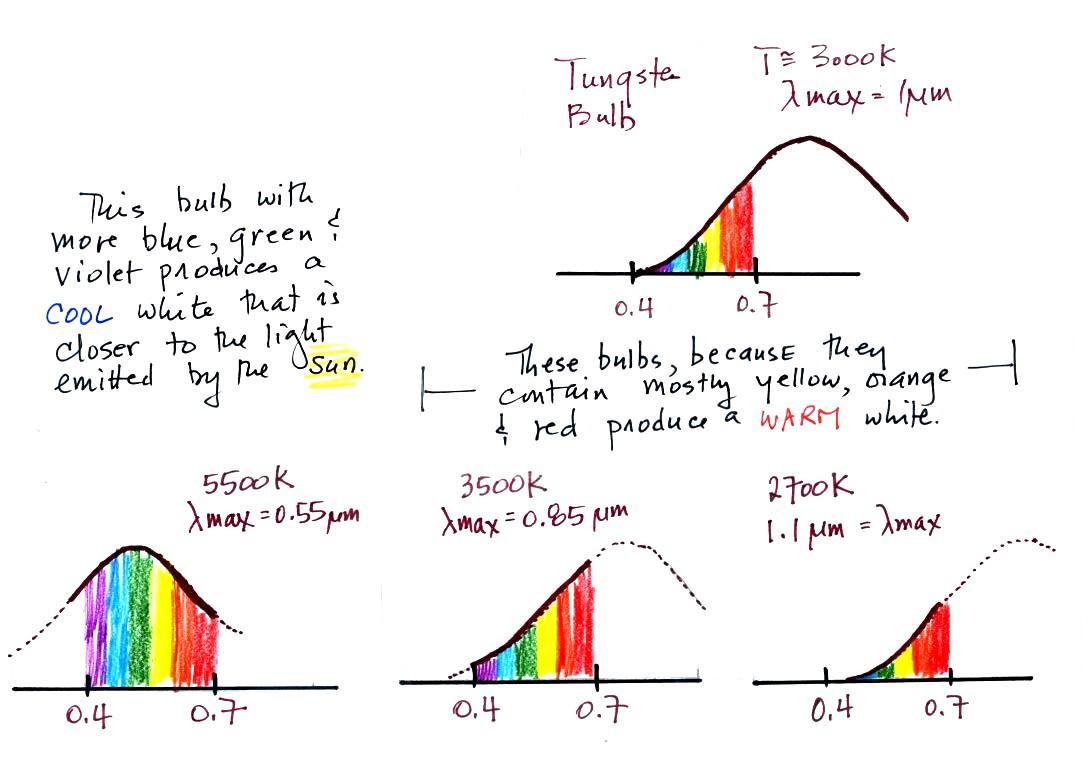
come with different color temperature ratings.
The bulb with the hottest temperature rating (5500 K ) in the
figure above is meant to mimic or simulate sunlight
(daylight). The temperature of the sun is 6000 K and
lambda max is 0.5 micrometers. The spectrum of the 5500
K bulb is similar.
The tungsten bulb (3000 K) and the CFLs with temperature
ratings of 3500 K and 2700 K produce a warmer white.
Three CFLs with the temperature ratings above were set up
in class so that you could see the difference between warm and
cool white light. Personally I find the 2700 K bulb "too
warm," it makes a room seem gloomy and depressing (a student
in class once said the light resembles Tucson at night).
The 5500 K bulb is "too cool" and creates a stark
sterile atmosphere like you might see in a hospital
corridor. I prefer the 3500 K bulb in the middle.
The figure below is from an
article on compact fluorescent lamps in Wikipedia for
those of you that weren't in class and didn't see the bulb
display. You can see a clear difference
between the cool white bulb on the left in the figure below
and the warm white light produced by a tungsten bulb (2nd from
the left) and 2 CFCs with low temperature ratings (the 2 bulbs
at right).
There is one downside to these energy efficient CFLs.
The bulbs shouldn't just be discarded in your ordinary
household trash because they contain mercury. They
should be disposed of properly (at a hazardous materials
collection site or perhaps at the store where they were
purchased).
It probably won't be long before LED bulbs
begin to replace tungsten and CFL bulbs. The price has
dropped significantly in just the last 6 months or so.