Monday Mar. 18, 2013
Joe Bonamassa "Driving
Towards the Daylight"
1st part of the next bunch of material:
This is on p. 83 in the ClassNotes.

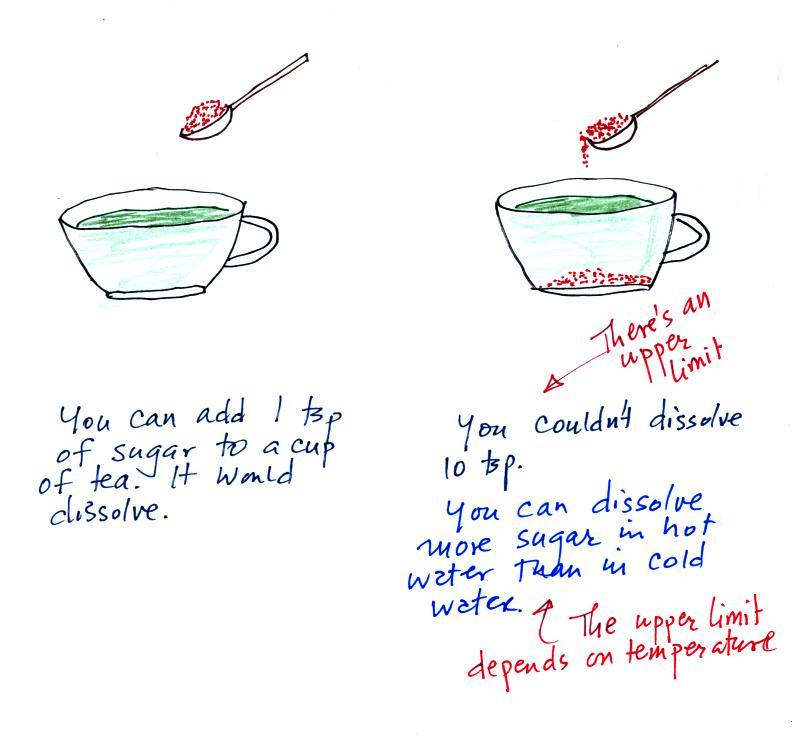
Basically the same idea
as teaspoons of sugar mixed into a cup of tea.
The sugar dissolved in
tea analogy is still helpful.
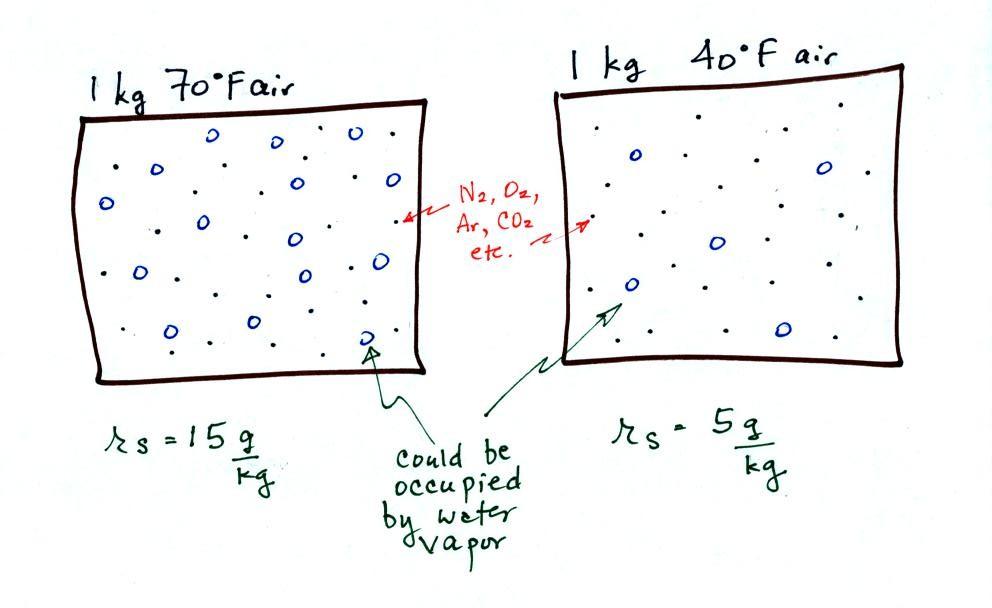
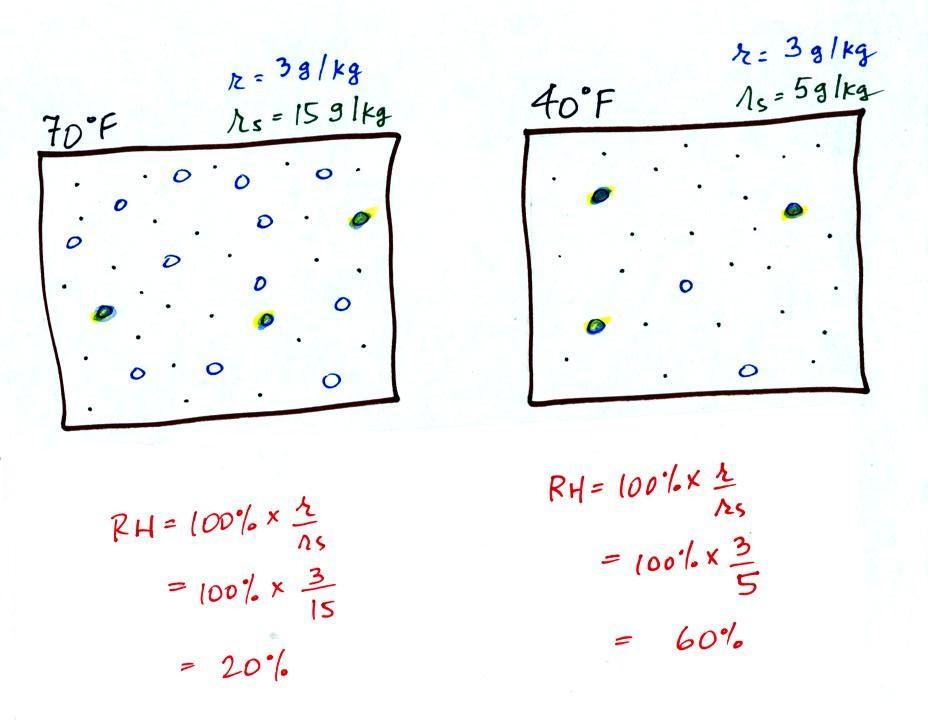
Each of the open circles
represents 1 gram of water vapor that the air
could potentially hold.
We haven't said anything about how much water vapor is
actually in the air.
The numbers 15 and 5 came from the table on p. 86.
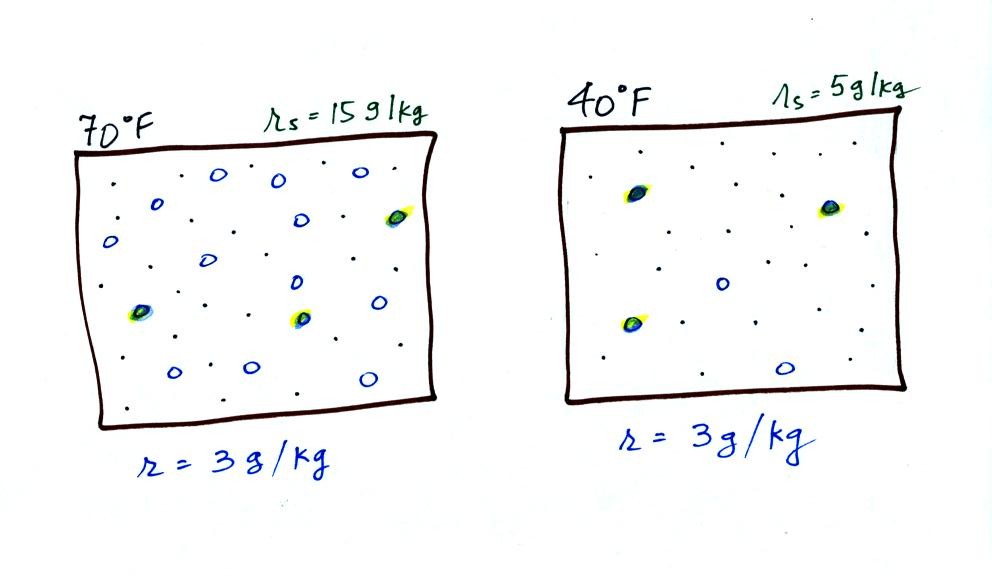
Now we have gone and added some water vapor, the same amount
of water vapor,
to both parcels of air.
Maybe you can begin to figure out what
relative humidity might mean.
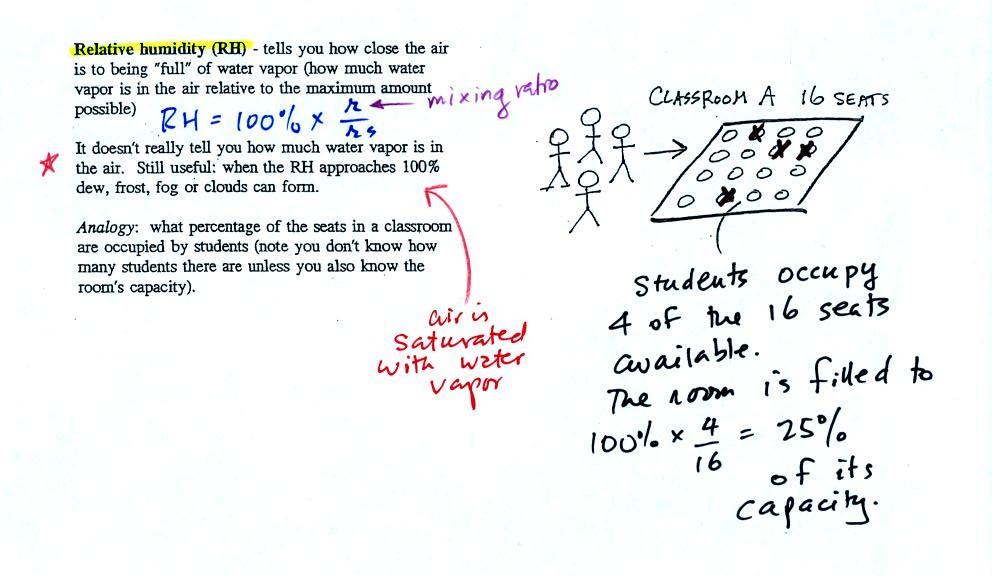
Note: RH doesn't really tell you how much water
vapor is actually in the air.
We'll be making use of job #2 a lot in the next class or
two.
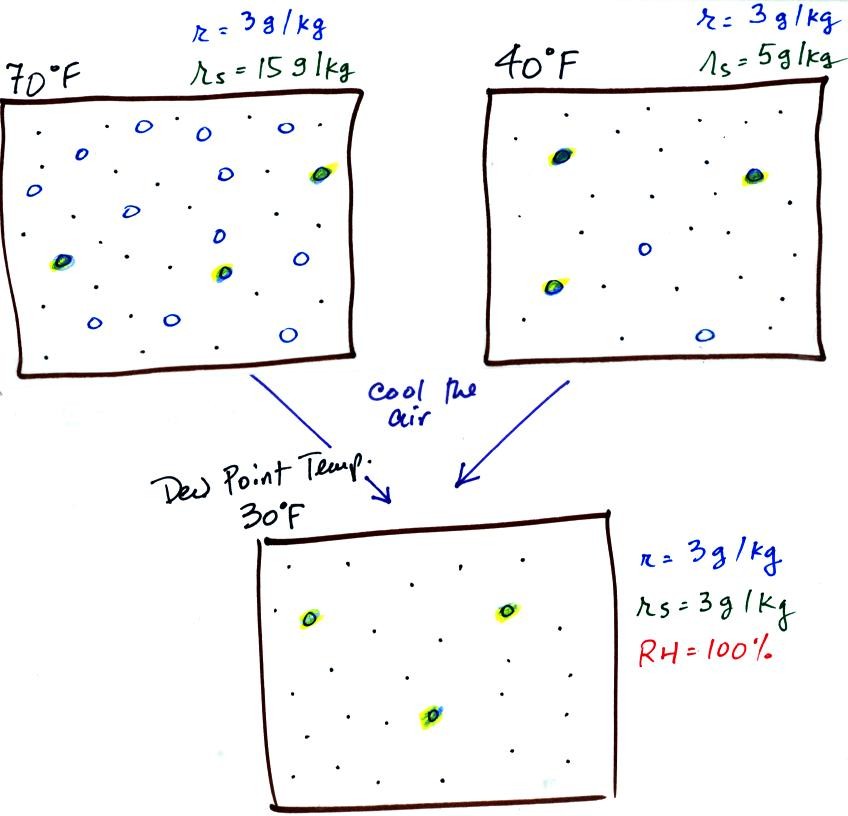
Both parcels contains the same actual amount of water
vapor (they have the same mixing ratio)
They both have the same dew point temperature.
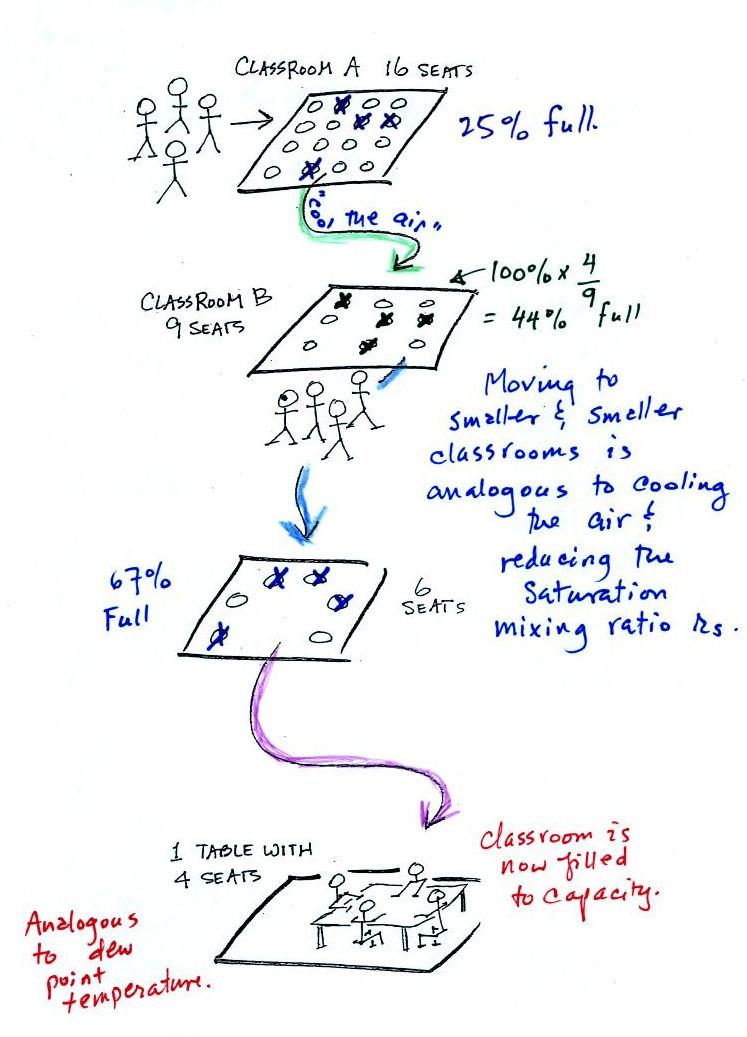
Now back to
the student/classroom analogy.
Doe_J
quiz1 -55 (195
pts possible) 71.8%
quiz2 -52 (170
pts possible) 71.5%
1.0 EC points
(2.1 pts possible,class average is 0.95)
writing scores:
34.0 (expt/book report) + 15.5 (1S1P pts (average is
15.5))
writing
percentage grade estimate: 89.2%
average (no quiz
scores dropped): 75.2% + 1.0 = 76.1%
average (lowest quiz score dropped): 76.1% + 1.0 =
77.1%
We need to try to learn a little bit more about saturation of
air.
In particular why is there an upper limit to the amount of water
vapor that can be found in air?
Why does the upper limit depend on temperature?
Could you tell the difference between cups of hot and
iced tea, even if you couldn't see the ice cubes in the iced
tea?
Hot water evaporates
more rapidly than cold water.
We'll cover both cups
so that water vapor can begin to buildup in the air above
the water in both cups.
Arrows represent the different rates of
evaporation. I just made up the numbers 10 and
30. The important thing is that the warm water is
evaporating more quickly than the cold water.
Water vapor will start to buildup in the air above each
cup. And, even though it has just evaporated, some of
the water vapor will condense and rejoin the water at the
bottom of each cup. Let's just assume that 1% of the
water vapor molecules will condense (again just a made up
number).
The amount of water vapor in each glass will increase
until it reaches a point where
water evaporation
rate = water vapor condensation rate
for the cup of cold
water
10 = 0.01 x water
vapor concentration
The 0.01 is 1% expressed in decimal form. Solving
this
equation
gives
you a water vapor concentration of 1000. The air is
saturated when you reach this point and the RH = 100%.
The saturation water vapor concentration in the air in
the warm cup would be 3000.
same in both glasses
|
different
|
saturated air
RH = 100%
rate of evaporation = rate of condensation
|
actual amount of water vapor in the
air
|
The fact that the rates of evaporation and condensation
are equal when air is saturated (RH = 100%) is something
we'll be using later when we study the formation of
precipitation. Here's a picture of how that would look
inside a cloud.
The air inside the cloud is saturated. The rate
of evaporation from the cloud droplet (2 green arrows) is
balanced by an equal rate of condensation (2 orange
arrows). The RH = 100%. The cloud droplet won't
grow any bigger or get any smaller.
Here's something to test your understanding of this
material.
What information can you add to this picture? Is the
water in Glass A WARMER or COLDER
than in Glass B? Is there MORE or
LESS water vapor in the air in Glass A than in Glass
B? Is the relative humidity in each glass MORE than
100%, LESS than 100% or is it EQUAL to 100%. The rates
of evaporation and condensation aren't equal in either
glass, so the pictures will change with time. What
will the glasses look once they have reached
equilibrium? Click here when
you think you know the answers.