Wednesday Mar. 20, 2013
click here to download today's notes
in a more printer friendly format
Some music, "Like
I Do", from Rupa and the April Fishes to get my newly
acquired jumping beans dancing before class today.
Ultimately a grand total of 3 students found the short Optional Assignment
that was hidden in Monday's online notes. Don't
worry if you didn't do the assignment, it was only worth 0.15
extra credit points. A somewhat longer Optional Assignment,
worth 0.5 points, was handed out in class today. This latest
assignment is due Mon., Mar. 25.
Roughly the first half of class today involved working through
a couple of humidity problems. As you work through the
problems you will, hopefully, begin to better understand roles of
the various humidity variables and when and why their values
change.
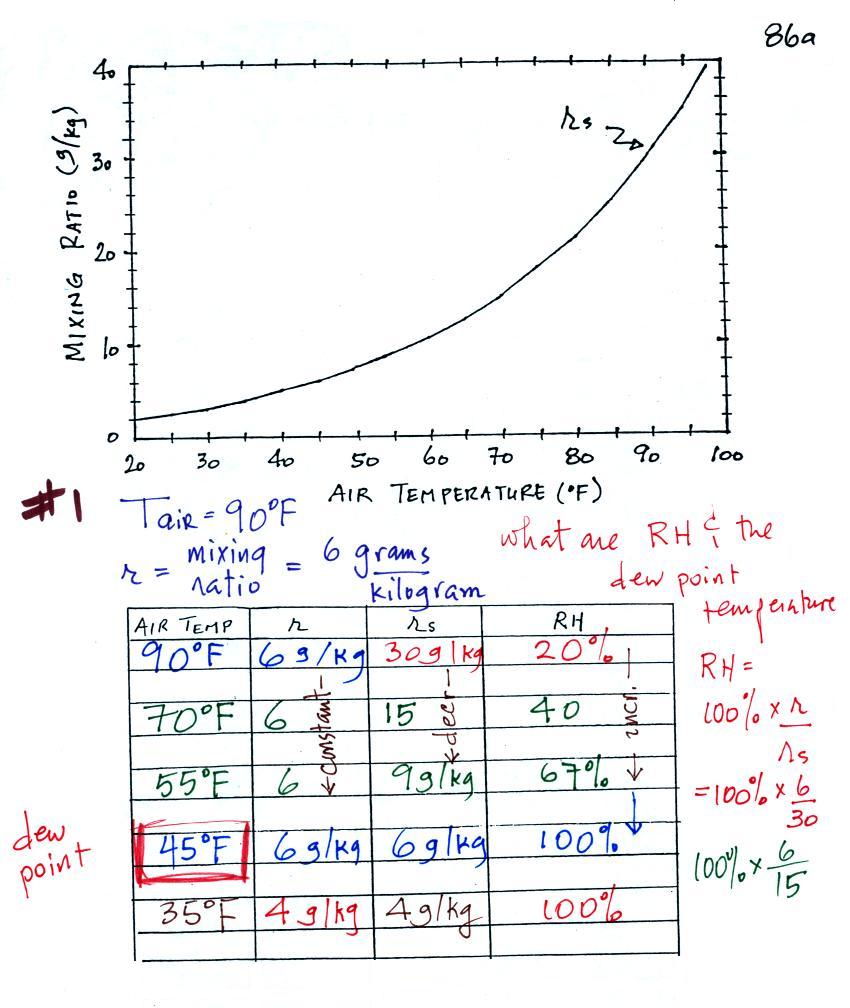
Example #1
I gave my notes from class to a student so I'm
using notes from a previous class.
In this example you are given an air temperature of 90 F and a
mixing ratio value of 6 g/kg. You are supposed to determine
the mixing ratio and the dew point temperature.
These notes from class would be hard enough to sort out even if
you were in class. So we'll work through this problem in a
more detailed, step-by-step manner.
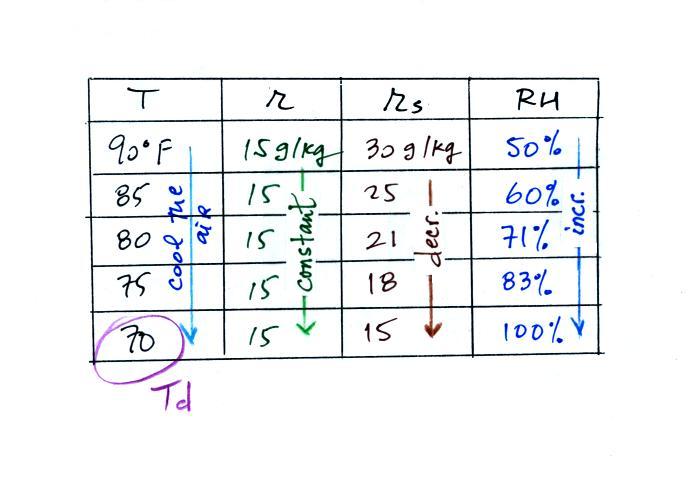
We're given an air temperature of 90 F and a mixing ratio (r) of 6
g/kg. We're supposed to find the relative humidity
(RH) and the dew point temperature. We start by
entering this data in the table.
Anytime you know the air's temperature you can look up
the saturation mixing ratio value on a chart (such as the one on
p. 86 in the ClassNotes); the saturation mixing ratio is 30 g/kg
for 90 F air. 90 F air could potentially hold 30 grams of
water vapor per kilogram of dry air (it actually contains 6 grams
per kilogram in this example).
Once you know mixing ratio and saturation mixing ratio you can
calculate the relative humidity (you divide the mixing ratio by
the saturation mixing ratio, 6/30, and multiply the result by
100%). You ought to be able to work out the ratio 6/30 in
your head (6/30 = 1/5 = 0.2). The RH is 20%.
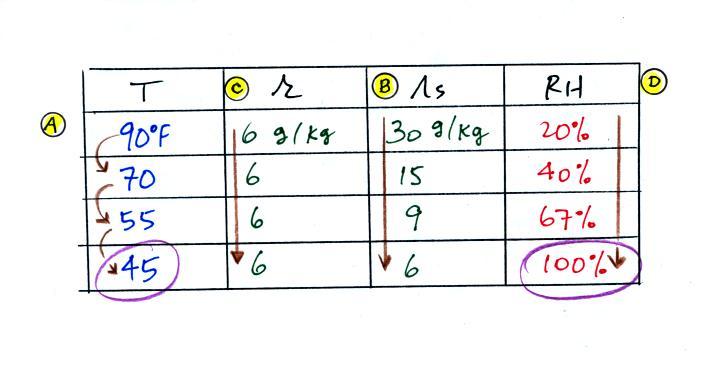
The numbers we just figured out are shown on the top line above.
(A) We imagined cooling the air from 90F to 70F, then to 55F, and
finally to 45F.
(B) At each step we looked up the saturation mixing ratio and
entered it on the chart. Note that the saturation mixing
ratio values decrease
as the air is cooling.
(C) The mixing ratio
(r) doesn't change as we cool the air. The only
thing that changes r is adding or removing water vapor and we
aren't doing either. This is probably the most difficult
concept to grasp.
(D) Note how the relative humidity is increasing as we cool the
air. The air still contains the same amount of water vapor
it is just that the air's capacity is decreasing.
Finally at 45 F the RH becomes 100%. This is kind of a
special point. You have cooled the air until it has become
saturated. The dew point temperature in this
problem is 45 F.
What would happen if we cooled the air further still,
below the dew point temperature?
35 F air can't hold the 6 grams of water vapor that 45 F air
can. You can only "fit" 4 grams of water vapor into the 35 F
air. The remaining 2 grams would condense. If this
happened at ground level the ground would get wet with dew.
If it happens above the ground, the water vapor condenses onto
small particles in the air and forms fog or a cloud. Because
water vapor is being taken out of the air (the water vapor is
turning into water), the mixing ratio will decrease from 6 g/kg to
4 g/kg. As you cool air below the dew point, the RH stays
constant at 100% and the mixing ratio decreases.
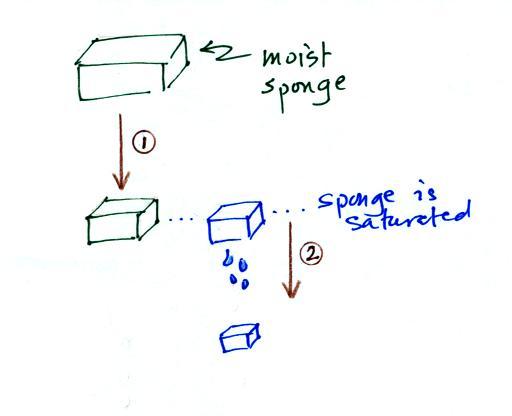
In many ways cooling moist air is liking squeezing a
moist sponge (this figure wasn't shown in class)
Squeezing the sponge and reducing its volume is like cooling moist
air and reducing the saturation mixing ratio. At first (Path
1 in the figure) when you squeeze the sponge nothing happens, no
water drips out. Eventually you get to a point where the
sponge is saturated. This is like reaching the dew
point. If you squeeze the sponge any further (Path 2) water
will begin to drip out of the sponge (water vapor will condense
from the air).
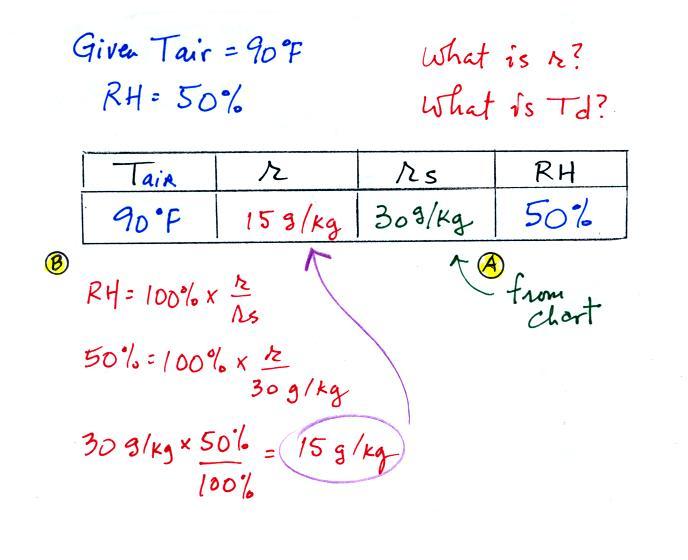
Example 2
We're given an air temperature of 90 F and a
relative humidity of 50%; we'll try to figure out the mixing ratio
and the dew point temperature. Here's something like what we
ended up with in class.
The problem is worked out in detail below:
First you fill in the air temperature and the RH data
that you are given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing ratio in
your head. Air that is filled to 50% of its capacity could
hold up to 30 g/kg. Half of 30 is 15, that is the mixing
ratio. Or you can substitute into the relative humidity
formula and solve for the mixing ratio. The details of that
calculation are shown above at B.
Finally you imagine cooling the air. The saturation mixing
ratio decreases, the mixing ratio stays constant, and the relative
humidity increases. In this example the RH reached
100% when the air had cooled to 70 F. That is the dew point
temperature.
We can use results from humidity problems #1 and #2 to learn and
understand a useful rule.
In the first example the difference between the air and
dew point temperatures was large (45 F) and the RH was
low (20%).
In the 2nd problem the difference between the air and dew point
temperatures was smaller (20 F) and the RH was higher (50%).
The easiest way to remember this rule is to remember the case
where there is no difference between the air and dew point
temperatures. The RH then would be 100%.
That was about all the time we had for relative humidity in
class today. We'll do a couple more example problems on
Friday.
Today is the Spring Equinox (it was actually at
4:02 am MST).
We can't let a big event like that go
unnoticed. The Fall Equinox will be
on Sept. 22 this year.

The figure above shows the
earth orbiting the sun.
On or around Dec. 21st, the winter solstice, the north
pole is tilted away from the sun. Note that a small
portion of the earth near the N. Pole (north of the Arctic
Circle) spends 24 hours in darkness. Days are less
than 12 hours long in the northern hemisphere and the sun
is low in the sky. Both factors reduce the amount of
sunlight energy reaching the ground. That's why it's
cold and wintry.
On June 21st, the summer solstice, the north pole is
tilted toward the sun. Now there are 24 hours of
sunlight north of the Arctic Circle. Days are more
than 12 hours long in the northern hemisphere and the sun
is high in the sky at noon. A lot more sunlight
energy reaches the ground; that's why it is summer.
The equinoxes are a time of transition. On the
equinoxes, the N. Pole still tilted just not toward or
away from the sun. The line separating day and night
passes through the pole and the days and nights are each
about 12 hours long everywhere on earth (except perhaps at
the poles).
The drawing below shows you what you would see at sunrise
(about 6:30 am) on the Spring Equinox here in Tucson (the same
would happen on the Fall Equinox).
The sun
rises exactly in the east on the equinoxes. The rest of
the year it is a little to the north or south of east.

At noon you would need to look
due south to see the sun.
The sun reaches its
highest point in the sky at noon. On the equinoxes in
Tucson that's almost 60 degrees. The sun is lower in
the sky (34.5 degrees above the horizon) on the winter
solstice. That together with the fact that the days
are shorter means much less sunlight energy reaches the
ground. In the summer the days are longer and the sun
gets much higher in the sky at noon (81.5
degrees above the horizon, nearly overhead). Much more
sunlight energy reaches the ground and it is much warmer.
The sun passes directly overhead at the equator at noon on
the equinoxes.

The sun sets
exactly in the west on the equinoxes at about 6:30 pm in
Tucson.
This is the 2 pm class.
Most of you are more likely (perhaps) to see the sun set than
see the sun rise. The figure below shows you about what
you would see if you looked west on Speedway (from Treat Ave.)
at sunset. In the winter the sun will set south of west,
in the summer north of west (probably further south and north
than shown here). On the equinoxes the sun sets exactly
in the west. This is something you should check out for
yourself this week before the sun moves noticeably to the
north of due west.
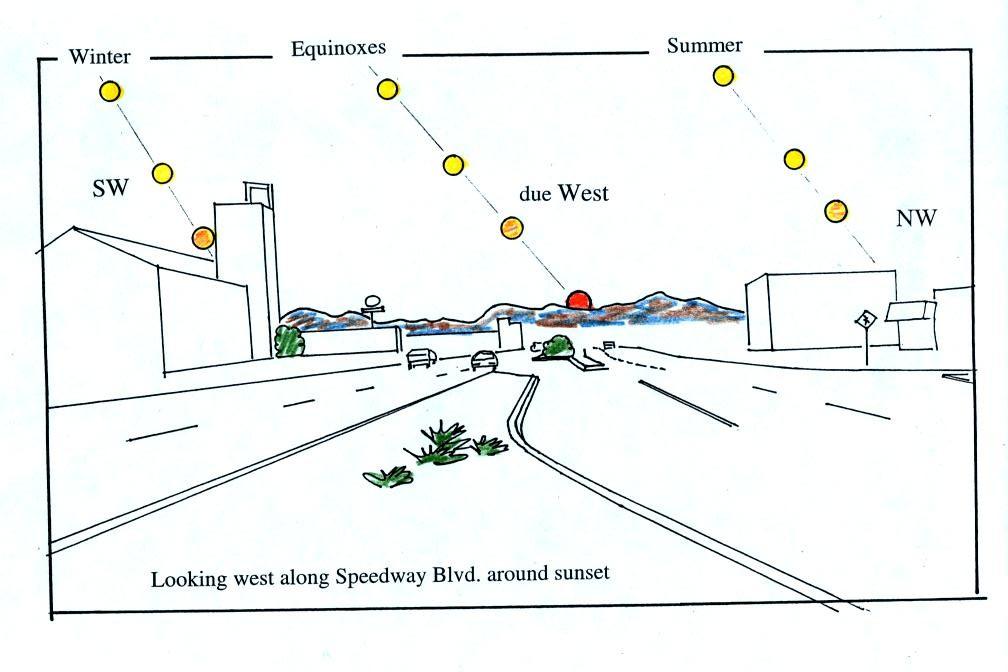
Something else to note in this figure.
Note how the sun is changing color. It changes
from a bright yellow white to almost red by the time it
sets.. This is due to scattering of sunlight by
air. The shorter wavelengths (violet, blue, green) are
scattered more readily than the longer wavelengths. At
sunset the rays of sunlight take a much longer slanted path
through the atmosphere and most of the shorter wavelengths are
scattered and removed from the beam of sunlight. All
that's left in the beam of light that reaches your eyes are
the longer wavelengths: yellow, orange, and red.
You
might have noticed that the sketch seems to be
pretty carefully drawn. That's because
several years ago I positioned myself in the
median near the intersection of Treat and Speedway
and pointed my camera west. I took a
multiple exposure photograph of the sun over a 2
or 3 hour period that ended at sunset.
Here's the photo I ended up with (it's a copy of a
copy so that picture quality isn't all that
great):
If you
aren't careful, you can get yourself seriously injured,
even killed, on or around the equinoxes. Here's
an article that appeared in the Arizona Daily Star at
the time of the 2011 Fall equinox.
December 21, the
summer solstice, is the shortest day of the year (about 10
hours of daylight in Tucson). The days have slowly
been getting longer since then. The rate of change is
greatest at the time of the equinox.
This will continue up until June 21, the summer solstice,
when there will be about 14 hours of daylight. After
that the days will start to shorten again as we make our way
back to the winter solstice.
There
was a very interesting coincidence a few semester's ago.
We were covering some of this same material in class on
Friday Sep. 23. There were a few parents in class because it
was Parent's Weekend. I showed these same pictures on that
afternoon. One of the parents came up to the front after
class and mentioned having seeing the sun right at the end of 77th
St. in New York City around this time of year. That got me
thinking that a picture of sunset at the end of one of the long
streets with all the tall buildings might be spectacular.
When I started looking however I found that the major streets in
Manhattan aren't oriented EW and NS. You can see this on a Google
map of Manhattan. 77th St. is oriented in more of a
NW-SE direction. So the sun doesn't shine straight
down 77th St. at sunrise and sunset on the equinoxes. I was
pretty disappointed but then I stumbled on the this Manhattanhenge
map which shows the direction
of sunset (the left, west, side of the map) and sunrise (the
right, east, side of the map) at various times of the year.
If you remember that as you move past the Spring Equinox
toward summer sunrise move north of east and sunset is north of
west. On May 31 the sun has moved far enough north that it
does set right at the west end of 77th St. Sunset continues
to move north up until the summer solstice on June 21. Then
the sunset starts to move back south. You can again see the
sunset at the west end of 77th St. on July 12 and 13. Here's
a gallery
of Manhattanhenge images. That
would certainly make a worthwhile field trip in Atmo 170A1 if the
semester went that long. The "henge" part of the name comes
from Stonehenge
where the rising and setting sun aligns with stones on the
solstices.
Manhattanhenge is a little confusing and hard to figure
out. But do look at the photographs with the idea that you
can see something similar here in Tucson on the equinoxes (minus
all the tall buildings).
You can also see the sunrise at the east end of 77th St.
But sunrise has to be in the southeast. This takes place on
Dec. 5 and Jan. 8, just before and just after the winter solstice.