Newton's Law of Universal
Gravitation
Isaac Newton is one of the greatest scientists that ever
lived. Among other things, he formulated a Law of Universal
Gravitation that allows you to
calculate the gravitational attraction between two objects. With
a little thought you can understand why certain variables appear in
Newton's Law and why they
appear in either the numerator (direct proportionality) or in the
denominator (inverse proportionality).

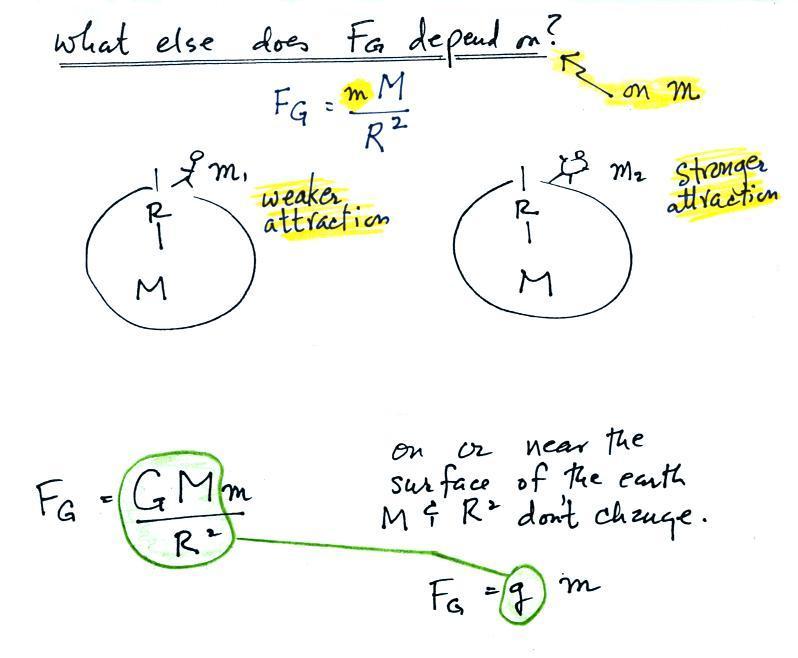
You probably intuitively understand that the gravitational
attraction
between two
objects (M and m in
the figures) depends
on the distance between the objects. The gravitational
force becomes weaker the further away the two objects are from each
other. The law of universal gravitation is actually an inverse
square law, the gravitational attraction between two objects is
inversely proportional to the square of the distance between the two
objects.
In the bottom part of the picture above and in the upper part of the
figure below we see that the attractive force
also depends on the masses of the two objects.
The complete formula is shown at the bottom of the page
above. G
is a constant. On the surface of the earth G, M, and don't
change. The gravitational acceleration, Rg, is just the
quantity [G
times Mearth
divided by ( Rearth )2
]. To
determine the
weight (on the earth's surface) of an object
with mass m you simply multiply m x g.
The figure below gives the Metric and English units of
mass
and weight. You have probably heard of pounds, grams, and
kilograms. You might not have heard of dynes and Newtons.
Unless you've taken a physics course, you've probably never heard of
slugs.