The data and results that we will be discussing come largely from experiments conducted at the Kennedy Space Center (KSC). A large (15 km x 25 km) network of electric field mills is operating at KSC to identify and warn of thunderstorm and lightning hazards. The pre-1995 configuration of the field mill network is shown in the figure below (source of this and the following three figures: J.M. Livingston and E.P. Krider, "Electric Fields Produced by Florida Thunderstorms," J. Geophys. Res., 83, 385-401, 1978). The network was upgraded in 1995.

The network that was operating up to 1995 had 0.1 second time resolution. That is fast enough to resolve a lightning flash, but not the individual return strokes that make up cloud to ground flashes. The dynamic range was -15 kV/m to +15 kV/m and E field signals were digitized with 30 V/m accuracy. The overall accuracy of an individual field mill was about 10%.
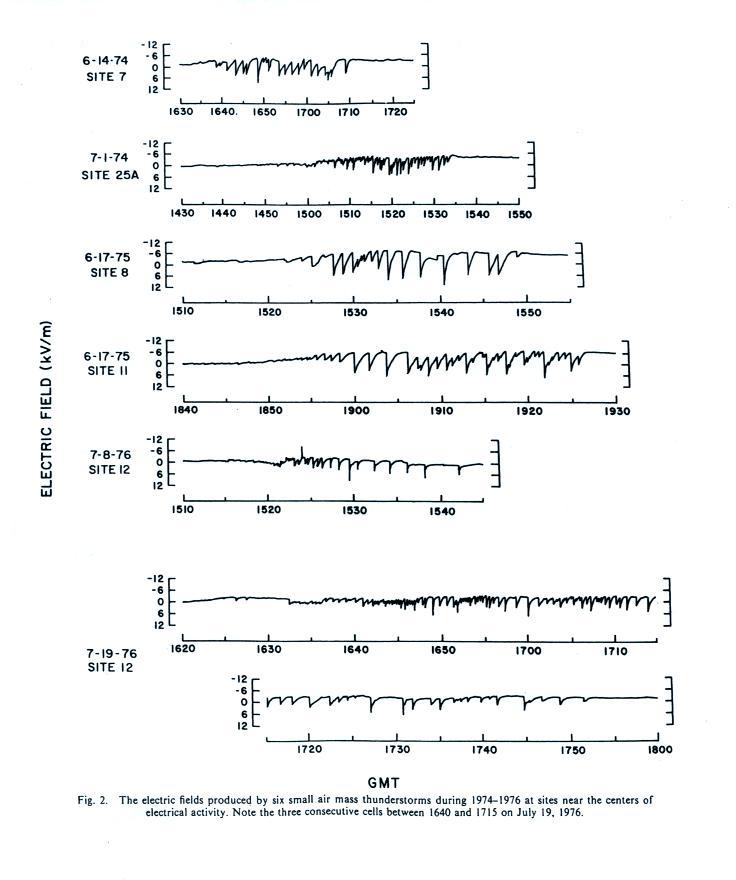
Examples of fields recorded during 6 small storms. Storms in this category lasted from 35 up to 85 minutes. Individual storms produced 16 to 82 discharges. The maximum flashing rate during a small storm is 1 flash/minute.
A single example of a large storm E field record is shown below

Storms like this are often broken into initial, very active, and end-of-storm-oscillation portions. Note the very slow but large amplitude oscillations in the final EOSO portion.
Large storms in the Livingston and Krider study had durations ranging from 75 to 265 minutes, produced 515 to 1212 discharges, and maintained flashing rates of 5 to 10 flashes per minute for 50 to 90 minutes. Number of flashes per 5 minute interval in a reprsentative large storm are shown in the histogram below.

It turns out we really won't be analyzing electric fields measured at the ground, rather the field changes, ΔE. The figure below explains why this is the case.

Fields measured at the ground
usually have lower amplitudes than fields measured just a
100 or 200 meters above the ground. Fields at the ground probably
wouldn't exceed 10
kV/m; fields just a few hundred meters above the ground could be
several times larger.
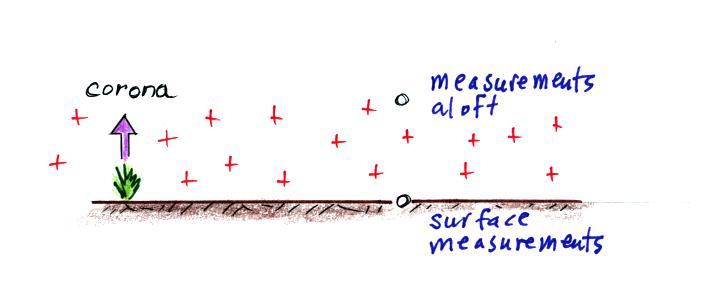
As the field at the ground begins to build after a lightning discharge, corona discharge from pointed objects and vegetation sprays space charge into the air above the ground. This limits the amplitudes of fields seen at the ground and affects the shape of the field recovery between flashes. We can't really get an accurate measurement of the thunderstorm field at the ground. You can, however, get an accurate measurement of the field change at the ground (it occurs so quickly that space charge can't be created or move quickly enough to affect the field change value).


As the field at the ground begins to build after a lightning discharge, corona discharge from pointed objects and vegetation sprays space charge into the air above the ground. This limits the amplitudes of fields seen at the ground and affects the shape of the field recovery between flashes. We can't really get an accurate measurement of the thunderstorm field at the ground. You can, however, get an accurate measurement of the field change at the ground (it occurs so quickly that space charge can't be created or move quickly enough to affect the field change value).

Measured field change values as a
function of distance (source: E.A.
Jacobson
and
E.P.
Krider,
"Electrostatic
Field
Changes
Produced
by
Florida Lightning," J. Atmos. Sci., 33, 103-117, 1976). Note
that small field change values are
sometimes observed very close to a discharge. We'll come back to
this observation later in today's notes.
Now lets start to look at what can be done when field change measurements are made at multiple locations on the ground.
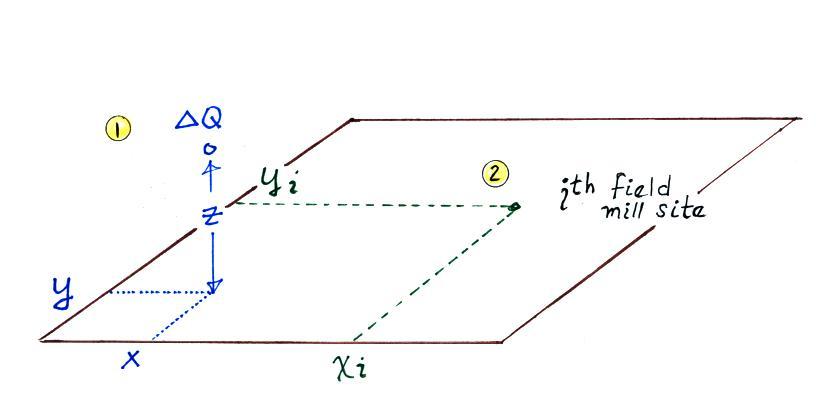
We'll consider the simplest model of a cloud-to-ground discharge
and
assume that the charge neutralized by the flash comes from a uniform
sphere of charge in the cloud. You can treat this as a single
point charge (Point 1). Our objective will be to use the delta E
measurements to determine the location (x, y, and z coordinates) and
magntitude of the neutralized charge (ΔQ).
We show the location of one of the field mill sites in the figure. At that location we will have a measurement of the field change, ΔEmi. We can also calculate the field change that the charge neutralized at Point 1 would produce at Point 2, the location of the ith field mill site. The expression for this calculated field change is shown below.
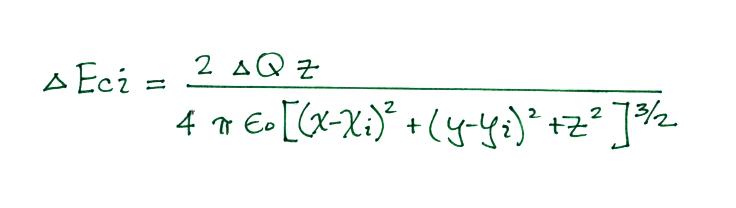
We're trying to determine ΔQ, x, y, and z. How can we calculate ΔEci if we don't know what they are? We make an initial guess about the location and the amount of charge neutralized during the lightning discharge. And we have field change measurements and can calculate field changes at the other field mill sites. We can adjust the values of x, y, z, and ΔQ until the chi-squared function below is minimized. That will give us our best estimate of ΔQ and its location.
Next we'll look at some results (source: the Jacobson and Krider, 1976 paper cited earlier)
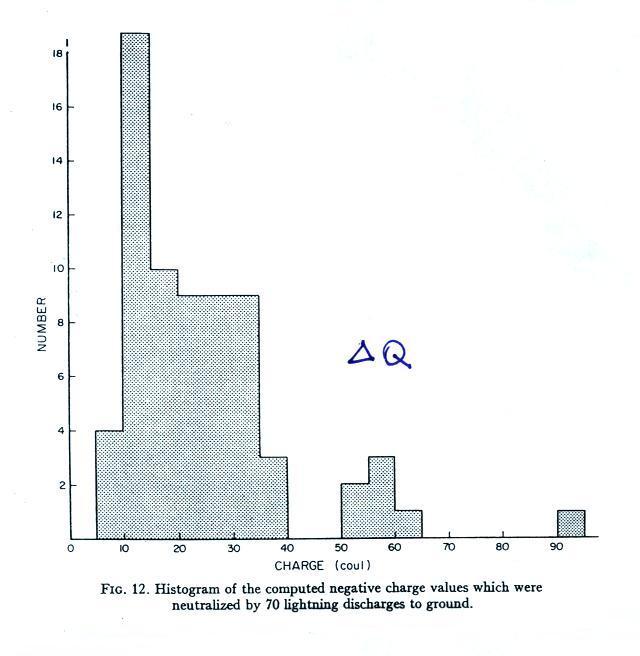
This first histogram gives solutions for ΔQ, the (negative) charge carried to ground in 70 cloud to ground discharges.
The next histogram shows that this charge was largely found between 6 and 9 or 10 km altitude.

Note that this corresponds to a -10o to -30o or -35o C temperature range (the -10o to -30o C range is highlighted above).
Finally the figure below shows that 75% of cloud-to-ground discharges strike the ground at a distance, D, of 5 km (3 miles) or less from the center of the charge neutralized by the flash. 95% of the discharges strike the ground within 8 km (5 miles) of the charge center. The distance D is defined in the figure below at right.
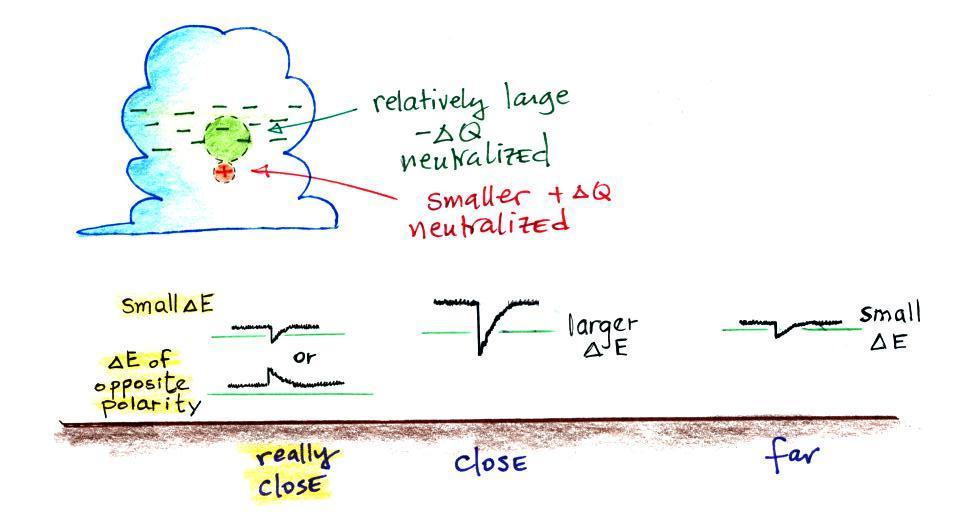
You would generally expect the field change amplitude to get larger as you get closer to a storm. We pointed out earlier however that the field amplitude is sometimes surprisingly small when you are very close to a storm. The field change may also switch polarity.
Now lets start to look at what can be done when field change measurements are made at multiple locations on the ground.

We show the location of one of the field mill sites in the figure. At that location we will have a measurement of the field change, ΔEmi. We can also calculate the field change that the charge neutralized at Point 1 would produce at Point 2, the location of the ith field mill site. The expression for this calculated field change is shown below.
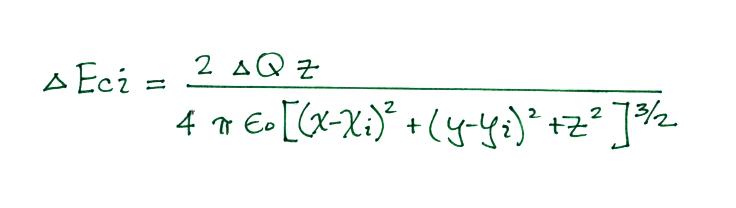
We're trying to determine ΔQ, x, y, and z. How can we calculate ΔEci if we don't know what they are? We make an initial guess about the location and the amount of charge neutralized during the lightning discharge. And we have field change measurements and can calculate field changes at the other field mill sites. We can adjust the values of x, y, z, and ΔQ until the chi-squared function below is minimized. That will give us our best estimate of ΔQ and its location.

Next we'll look at some results (source: the Jacobson and Krider, 1976 paper cited earlier)

This first histogram gives solutions for ΔQ, the (negative) charge carried to ground in 70 cloud to ground discharges.
The next histogram shows that this charge was largely found between 6 and 9 or 10 km altitude.

Note that this corresponds to a -10o to -30o or -35o C temperature range (the -10o to -30o C range is highlighted above).
Finally the figure below shows that 75% of cloud-to-ground discharges strike the ground at a distance, D, of 5 km (3 miles) or less from the center of the charge neutralized by the flash. 95% of the discharges strike the ground within 8 km (5 miles) of the charge center. The distance D is defined in the figure below at right.
 |
 |
You would generally expect the field change amplitude to get larger as you get closer to a storm. We pointed out earlier however that the field amplitude is sometimes surprisingly small when you are very close to a storm. The field change may also switch polarity.

These observations suggest that a
lower volume of positive charge
might be involved in cloud-to-ground discharges. This led to the
development of a 2 charge model, illustrated below.


This is the most general form of
the two charge model - the two charges can have different
magnitudes and can have completely different locations in space.
A variation on this is the point dipole model where the two charges are
of equal amplitude but
opposite polarity. Another model assumes the two charges are
aligned
vertically. The calculated field change expression now contains 8
unknowns (ΔQ1,
x1, y1, z1,
ΔQ2,
x2, y2, and z2).

Again you use pairs of measured and calculated fields and minimize
a chi-squared function to determine the optimal solution for these
charge and location variables.
The next two figures shows some of the results obtained with this arbitrary 2 charge model (source: M.J. Murphy, The Electrification of Florida Thunderstorms, PhD Dissertation, Univ. of Az., 1996)


The next two figures shows some of the results obtained with this arbitrary 2 charge model (source: M.J. Murphy, The Electrification of Florida Thunderstorms, PhD Dissertation, Univ. of Az., 1996)

The circles indicate charge
neutralized during lightning discharges, time and altitude are plotted
along the horizontal and vertical axes, respectively. Cross
hatched circles
are positive charge, open circles are negative charge. The radius
of the
circle is proportional to the amount of charge neutralized.
Both intracloud and cloud to ground discharges were occurring during this storm. An example of each is shown. Intracloud discharges involve positive charge in the main positive charge center located in the upper portion of the thundercloud and negative charge in the main negative charge center in the middle of the cloud. Cloud-to-ground discharges neutralize negative charge in the middle of the cloud and almost always involve some positive charge in one of the lower positive charge centers. The vertical dotted lines at the bottom edge of the figure indicate cloud-to-ground discharges detected and located by the National Lightning Detection Network.
The next figure is from a little more active thunderstorm cell.
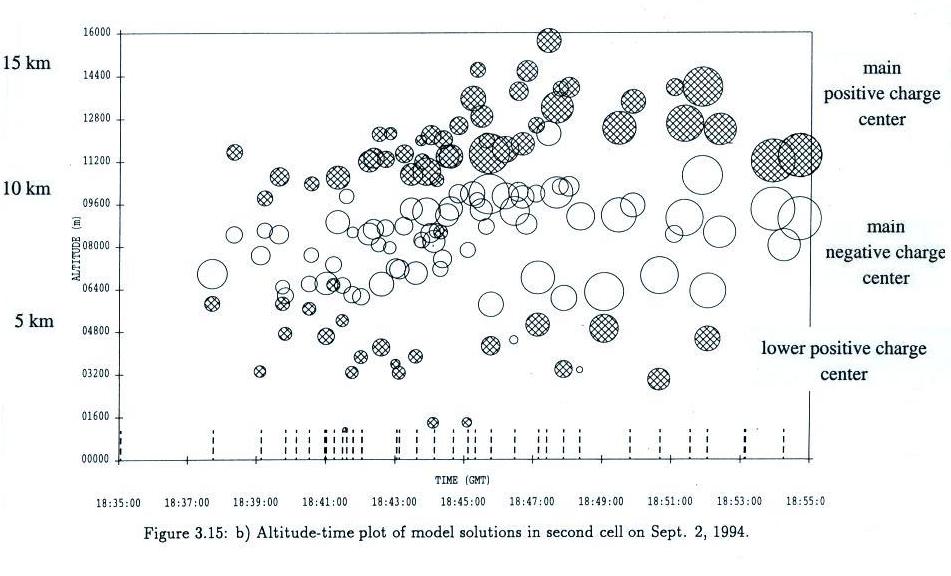
There seems to be a tendency for the amounts of charge neutralized in discharges to increase with time (larger diameter circles toward the end of the storm). The altitudes of the positive charges neutralized in intracloud discharges seem to move to higher altitudes in the middle and later portions of the storms.
The chi-squared procedure for determining charge center locations and charge magnitudes using multi-station field change measurements has also be used with slow E field antenna systems. Slow E records have faster time resolution and can accurately record the field changes produced by the separate return strokes in a cloud to ground flash. The results we looked at above were derived from field mill records and were an integration of all the processes that occur during a flash.
A photograph of one of the slow E field antennas is shown below at left. A schematic diagram of the antenna electronics is shown at right. The slow E network that we will be discussing was built and operated by researchers from the New Mexico Institute of Mining and Technology (P.R. Krehbiel, M. Brook, and R.A. McCrory, "An Analysis of the Charge Structure of Lightning Discharges to Ground," J. Geophys. Res., 84, 2432-2456, 1979).
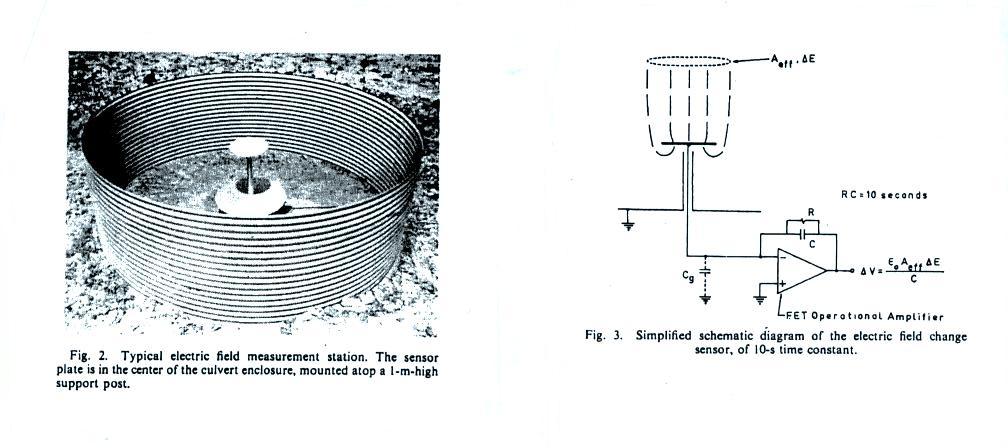
The antenna sensor plate is mounted about 1 m above the ground and
is surrounded by a culvert (probably to keep cattle and wildlife away
from the antenna. The decay time constant of the integrating
electronics was 10 seconds. It is worth pointing out that,
because the antenna plate is not mounted flush with the ground, its
effective area will be greater than its geometric area.
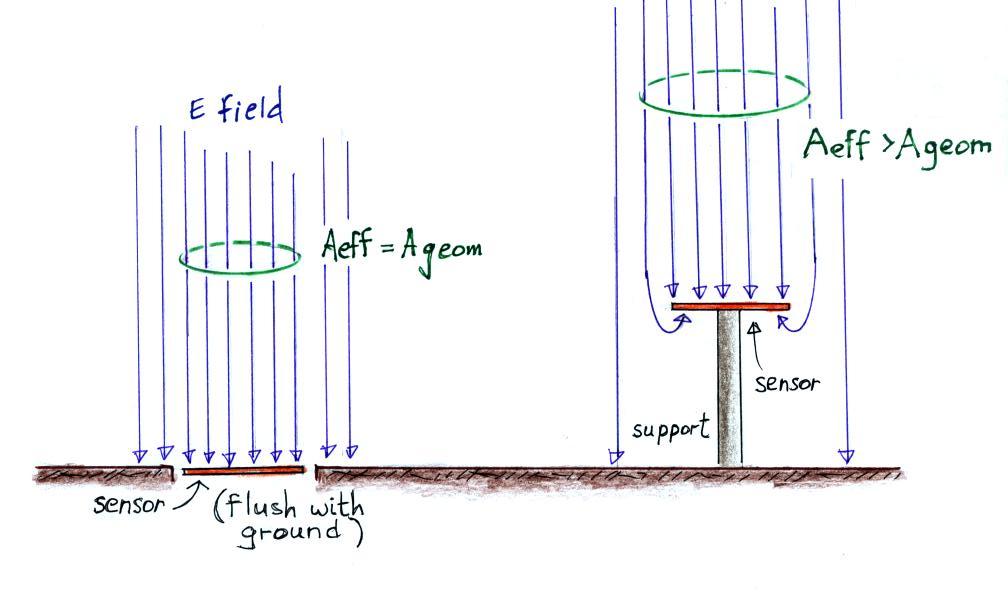
The effective crossectional area of a sensor plate positioned
above the ground is greater than its geometrical crossection.
Some of the E field lines that wouldn't strike a plate mounted flush
with the ground curl around and strike the sides or bottom of a plate
positioned above the ground. The effective area would need to be
determined by calibration.
The antenna network was installed near Socorro, New Mexico.
An example of a
CG flash slow E field record is shown in the figure below.
Six return strokes have been identified.
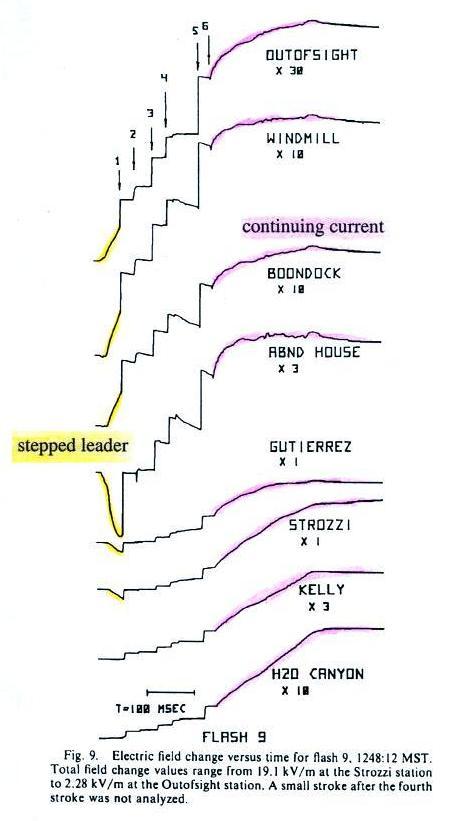
A stepped leader field change can be clearly see on several of the records and has been highlighted in yellow. The slow field change that follows the last return stroke is caused by a continuing current and has been highlighted in pink.
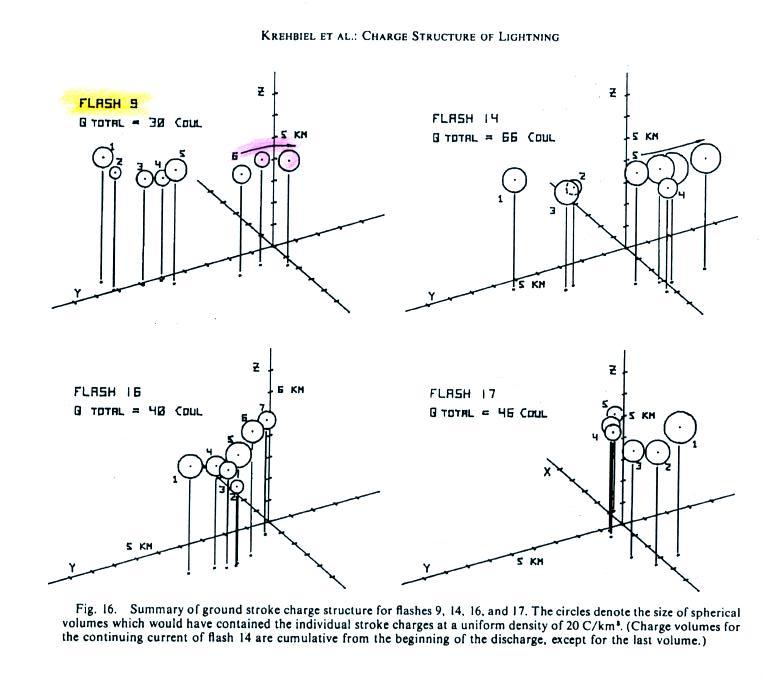
The figure below shows locations of the charges neutralized by the separate return stroke in 4 cloud-to-ground flashes. Flash 9 has been highlighted because those are the charge locations determined using the slow E field data shown above. Charge tapped by the continuing current that followed the 6th return stroke in Flash 9 has been highlighted in pink.
Both intracloud and cloud to ground discharges were occurring during this storm. An example of each is shown. Intracloud discharges involve positive charge in the main positive charge center located in the upper portion of the thundercloud and negative charge in the main negative charge center in the middle of the cloud. Cloud-to-ground discharges neutralize negative charge in the middle of the cloud and almost always involve some positive charge in one of the lower positive charge centers. The vertical dotted lines at the bottom edge of the figure indicate cloud-to-ground discharges detected and located by the National Lightning Detection Network.
The next figure is from a little more active thunderstorm cell.

There seems to be a tendency for the amounts of charge neutralized in discharges to increase with time (larger diameter circles toward the end of the storm). The altitudes of the positive charges neutralized in intracloud discharges seem to move to higher altitudes in the middle and later portions of the storms.
The chi-squared procedure for determining charge center locations and charge magnitudes using multi-station field change measurements has also be used with slow E field antenna systems. Slow E records have faster time resolution and can accurately record the field changes produced by the separate return strokes in a cloud to ground flash. The results we looked at above were derived from field mill records and were an integration of all the processes that occur during a flash.
A photograph of one of the slow E field antennas is shown below at left. A schematic diagram of the antenna electronics is shown at right. The slow E network that we will be discussing was built and operated by researchers from the New Mexico Institute of Mining and Technology (P.R. Krehbiel, M. Brook, and R.A. McCrory, "An Analysis of the Charge Structure of Lightning Discharges to Ground," J. Geophys. Res., 84, 2432-2456, 1979).


The antenna network was installed near Socorro, New Mexico.


A stepped leader field change can be clearly see on several of the records and has been highlighted in yellow. The slow field change that follows the last return stroke is caused by a continuing current and has been highlighted in pink.
The figure below shows locations of the charges neutralized by the separate return stroke in 4 cloud-to-ground flashes. Flash 9 has been highlighted because those are the charge locations determined using the slow E field data shown above. Charge tapped by the continuing current that followed the 6th return stroke in Flash 9 has been highlighted in pink.

In each case successive return
strokes tap separate volumes of charge that are further and further
away from the staring location.