
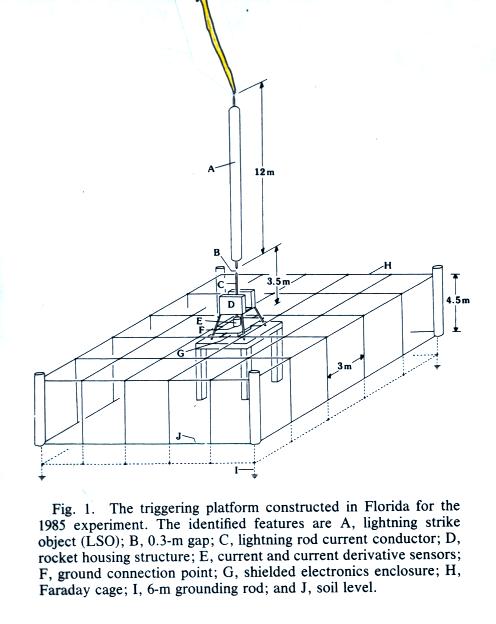
Point 1 is the location of the
triggering site. A rather complicated launch platform was in
place during
the 1985 experiments which may have affected the measurements and
interpretation of the results (Point 1a in the figure above and the
left
figure below which is from "Current
and
Electric
Field
Derivatives
in
Triggered
Lightning
Return
Strokes,"
C.
Leteinturier,
C.
Weidman,
and
J.
Hamelin,
J.
Geophys.
Res.,
95,
811-828,
1990.). A "cleaner" launch platform was
used
in 1987 (Point 1b in the figure above and the right photograph below
from "Submicrosecond
Intercomparison
of
Radiation
Fields
and
Currents
in
Triggered
Lightning
Return
Strokes
Based
on
the
Transmission-Line
Model,"
J.C.
Willett,
J.C.
Bailey,
V.P.
Idone,
A.
Eybert-Berard,
and
L.
Barret,
J.
Geophys.
Res.,
94, 13275-13286, 1989.).
E and dE/dt fields were recorded at Point 2, 5 km from the triggering site. At this range and at the time of peak E and peak dE/dt it is safe to assume the measured E fields were purely radiation fields. The water in the Mosquite Lagoon is brackish, a mixture of fresh water and salty ocean water. So propagation between the triggering site and the E field antennas was over a relatively high conductivity surface and high frequency signal content was preserved.
E field derivative signals were also recorded at Point 4, 50 meters from the trigger point. At this close range the dE/dt signals probably did contain induction and electrostatic field components.
Finally return stroke velocity were measured using high-speed streaking cameras at Point 5, located 2 km from the triggering point.

 |
 |
E and dE/dt fields were recorded at Point 2, 5 km from the triggering site. At this range and at the time of peak E and peak dE/dt it is safe to assume the measured E fields were purely radiation fields. The water in the Mosquite Lagoon is brackish, a mixture of fresh water and salty ocean water. So propagation between the triggering site and the E field antennas was over a relatively high conductivity surface and high frequency signal content was preserved.
E field derivative signals were also recorded at Point 4, 50 meters from the trigger point. At this close range the dE/dt signals probably did contain induction and electrostatic field components.
Finally return stroke velocity were measured using high-speed streaking cameras at Point 5, located 2 km from the triggering point.
Here's the basic idea behind the
experiment. The transmission line model predicts that the current
waveform (I) and the electric radiation field waveform (E) (also dI/dt
and dE/dt) will have
identical shapes similar to what is drawn below.
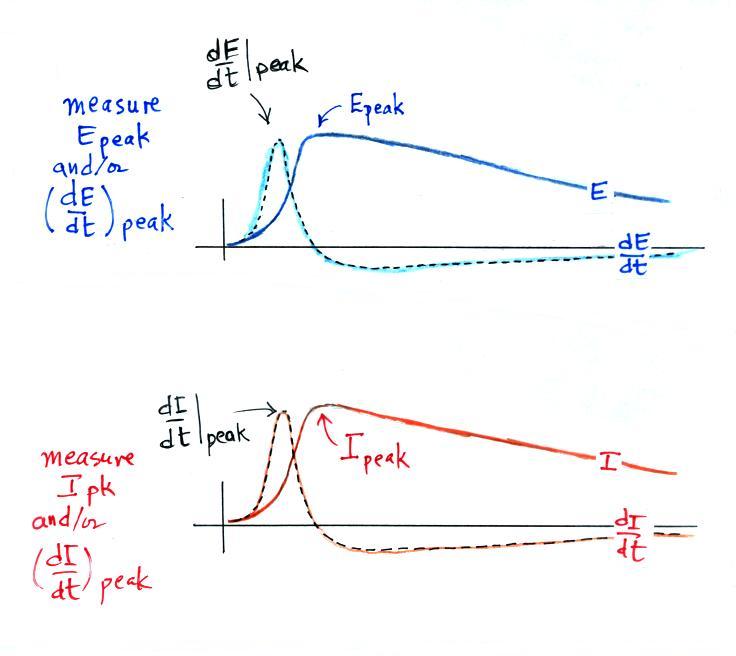
We measure Epeak and Ipeak and also (dE/dt)peak and (dI/dt)peak. We then insert these measurements into the transmission line model equations. D, the distance at which the field measurements were made, is known. We solve for the return stroke velocity, vTLM.
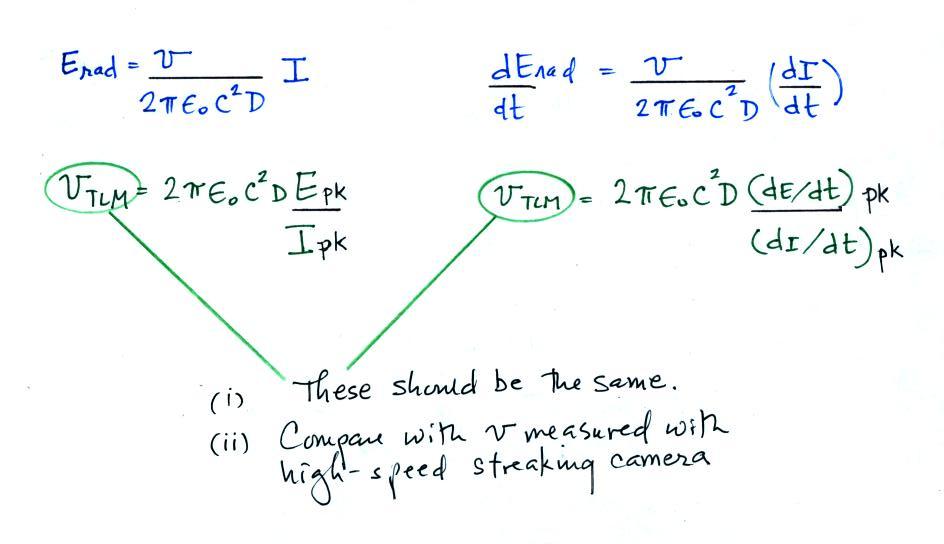
It shouldn't matter whether you use E and I data or dE/dt and
dI/dt measurements, the value of vTLM should be
the same.
Then you compare vTLM
with
the
velocity
measured
with
the
high-speed
streaking
camera.
The
next
figure
shows
how
things
turned
out.
(the
velocity
values
in
the
table
should all be multiplied by 108
m/s)
We measure Epeak and Ipeak and also (dE/dt)peak and (dI/dt)peak. We then insert these measurements into the transmission line model equations. D, the distance at which the field measurements were made, is known. We solve for the return stroke velocity, vTLM.


Let's first look at Points 1a and
1b. Point 1a shows vTLM
determined using the E and I measurements and the transmission line
model expression. Point 1b shows the measurements of return
stroke velocity. The value of vTLM obtained
for
the
1985
experiment
2.07
does
not agree very well with the measured value 1.26.
This may be due to the complicated launch platform. Agreement was
a
little better for the 1987 experiment.
At Point 2 we can see that vTLM using dE/dt and dI/dt is higher than the vTLM determined using E and I. This discrepancy has not been explained. The velocity values at Point 3 are appreciably higher than any of the other values. This estimate of vTLM was determined using dE/dt measured at 50 m distance from the triggering point. As we mentioned earlier, these fields probably contain induction and electrostatic field contributions and the transmission line model expression should probably not be used with them.
We haven't explained the Eshoulder column in the figure yet. A careful comparison of I and Erad signals (which the transmission line model predicts should be identical) shows some subtle differences between the two waveform shapes. Rather than just a single peak, the Erad signal often has a second somewhat smaller peak or shoulder as sketched below.
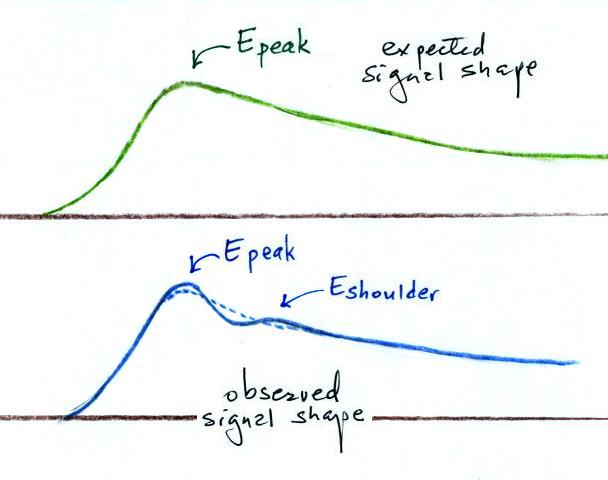
Much better agreement between vTLM and measured velocities was obtained when the Eshoulder amplitude was used with Ipeak in the transmission line expression when computing vTLM.
Now we'll look at one possible explanation of the Eshoulder feature (we mainly follow the discussion in the Leteinturier (1990) paper mentioned earlier)
We ordinarily think of the return stroke as being a single upward propagating current that begins at the ground. This view is shown in the figure above. Let's say a peak current of Io at the ground produces a field with a peak value Eo at some distance from the strike point.

It may be that the return stroke doesn't begin at the ground but a few 10s of meters above the ground at the junction point between the upward connecting discharge and the stepped leader. In this case there might not be just a single upward propagating current, rather currents might travel up and down from the junction point. The downward wave reaches the ground and is partially reflected. This kind of a situation, together with a few assumptions, can produce an E field signal that resembles the peak and shoulder features seen in the triggered lightning data.
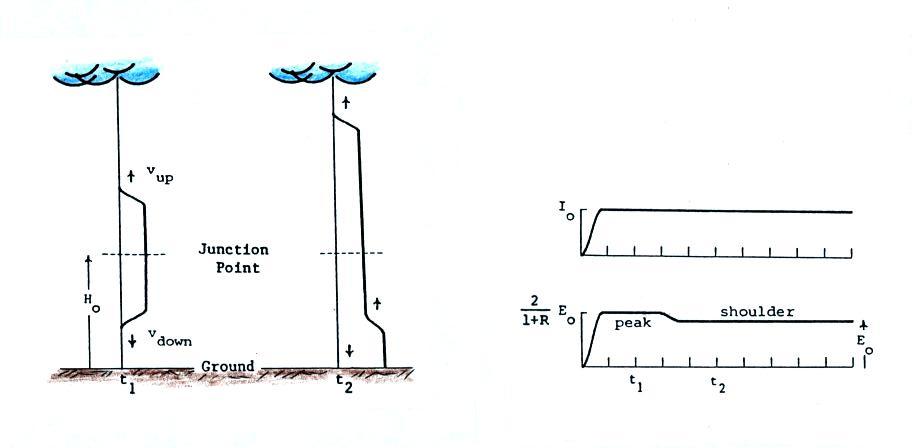
The figure below provides some justification for starting the return stroke above the ground, i.e. at the junction point between the upward connecting discharge and the bottom of the stepped leader channel. Positive charge would tend to travel upward, negative charge downward. This would result effectively in two upward pointing current waves.

Let's follow this a little further. We'll assume that the current rises to peak value before the downward wave reaches the ground.

A single upward propagating current with amplitude Io
will
produce a radiation field with amplitude Eo. What field will two
current waves each with amplitude Id produce? We need to find
some relation between Id and Io. To do that we need to look at
what happens when the downward traveling wave reaches the ground.
This is sketched in the figure below.
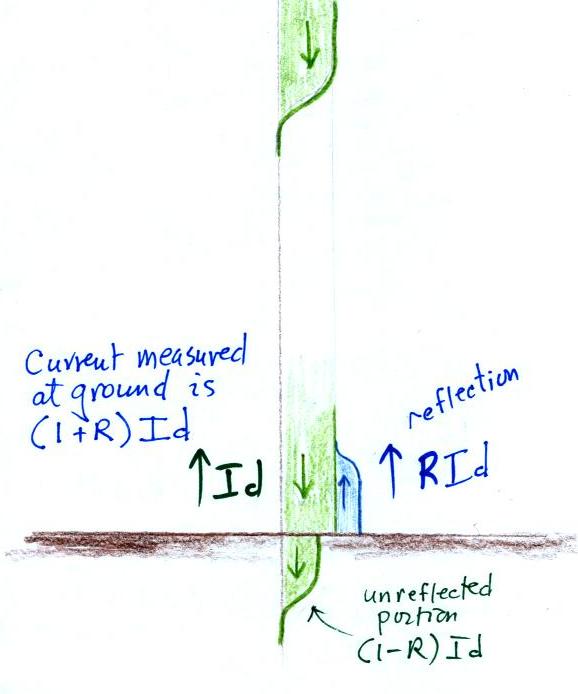
The top part of the figure shows the downward current
wave moving toward the ground. At the bottom of the figure we
show what happens when the wave reaches the ground. A portion of
the downward wave is reflected (shown in blue). We will assume
that the reflected current wave, which has amplitude R Id, and the
original wave, with amplitude Id,
add. So the total current
measured at the ground would be
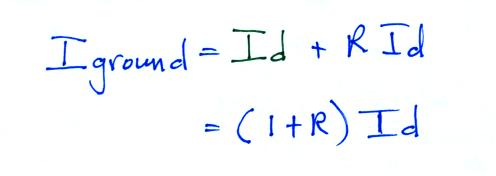
and we are going to force Iground to be equal to Io
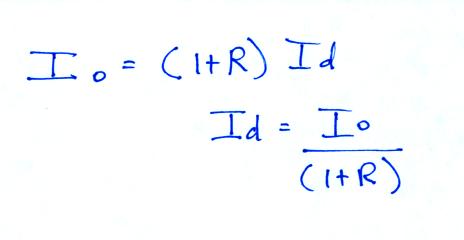
At Point 2 we can see that vTLM using dE/dt and dI/dt is higher than the vTLM determined using E and I. This discrepancy has not been explained. The velocity values at Point 3 are appreciably higher than any of the other values. This estimate of vTLM was determined using dE/dt measured at 50 m distance from the triggering point. As we mentioned earlier, these fields probably contain induction and electrostatic field contributions and the transmission line model expression should probably not be used with them.
We haven't explained the Eshoulder column in the figure yet. A careful comparison of I and Erad signals (which the transmission line model predicts should be identical) shows some subtle differences between the two waveform shapes. Rather than just a single peak, the Erad signal often has a second somewhat smaller peak or shoulder as sketched below.

Much better agreement between vTLM and measured velocities was obtained when the Eshoulder amplitude was used with Ipeak in the transmission line expression when computing vTLM.
Now we'll look at one possible explanation of the Eshoulder feature (we mainly follow the discussion in the Leteinturier (1990) paper mentioned earlier)
We ordinarily think of the return stroke as being a single upward propagating current that begins at the ground. This view is shown in the figure above. Let's say a peak current of Io at the ground produces a field with a peak value Eo at some distance from the strike point.

It may be that the return stroke doesn't begin at the ground but a few 10s of meters above the ground at the junction point between the upward connecting discharge and the stepped leader. In this case there might not be just a single upward propagating current, rather currents might travel up and down from the junction point. The downward wave reaches the ground and is partially reflected. This kind of a situation, together with a few assumptions, can produce an E field signal that resembles the peak and shoulder features seen in the triggered lightning data.

The figure below provides some justification for starting the return stroke above the ground, i.e. at the junction point between the upward connecting discharge and the bottom of the stepped leader channel. Positive charge would tend to travel upward, negative charge downward. This would result effectively in two upward pointing current waves.

Let's follow this a little further. We'll assume that the current rises to peak value before the downward wave reaches the ground.
The waves
might travel at 1/3 the speed of light, 1 x 108 m/s.
If the
current peaks in 0.1 microseconds, the junction point would need to be
at least 10 m above the ground. If it takes 1 microsecond for the
current to reach peak the junction point would need to be 100 m high
(that seems a bit much).


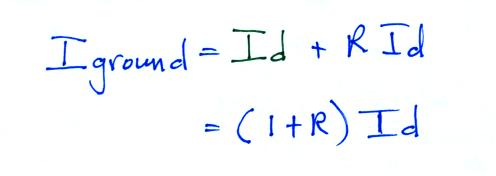
and we are going to force Iground to be equal to Io
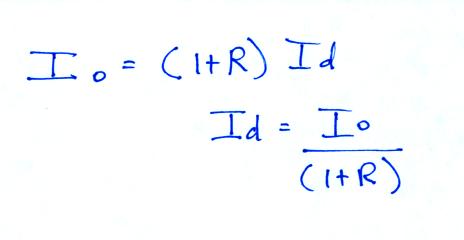
so that from the point of
view of the
current
measured at the ground, the two versions of return stroke initiation (a
single upward propagating current wave that starts at the ground versus
upward and downward pointing current waves that start at a junction
point above the ground) are indistinquishable. The same current
waveform
would be measured at the ground in both cases.
Now that we can relate Id and Io we can go back to our earlier figure
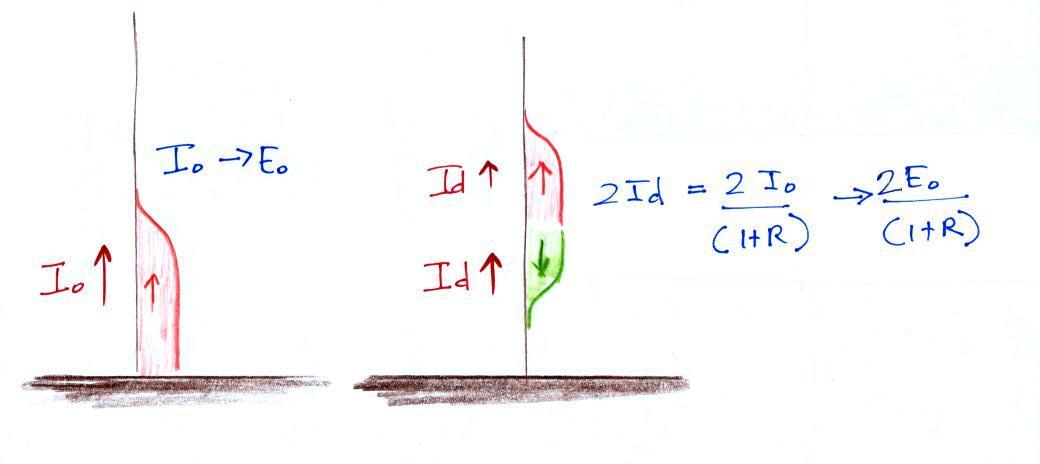
One current wave with amplitude Io produces a field Eo. Two current waves, each with amplitutde Id, produce a field with a peak value of n why the E field from the 2 current waves peaks at 2Eo/(1+R). So we've explained part of the figure below (the amplitude of the E field peak highlighted in yellow).
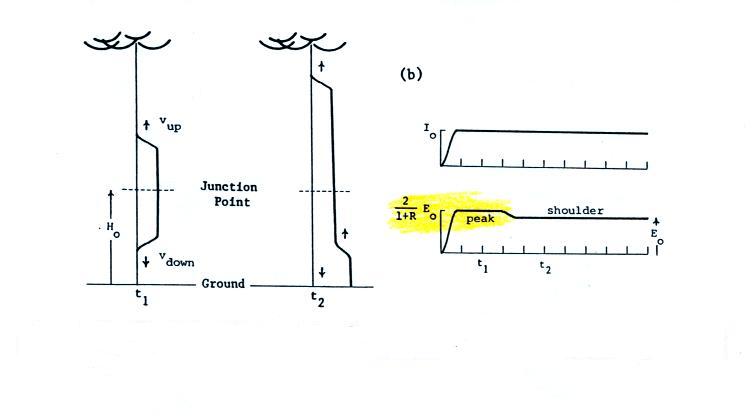
Now that we can relate Id and Io we can go back to our earlier figure

One current wave with amplitude Io produces a field Eo. Two current waves, each with amplitutde Id, produce a field with a peak value of n why the E field from the 2 current waves peaks at 2Eo/(1+R). So we've explained part of the figure below (the amplitude of the E field peak highlighted in yellow).

Now we need to explain
why the
field decreases and forms a shoulder and why the shoulder amplitude is
Eo. To do that we need to consider the unreflected portion of the
current wave.
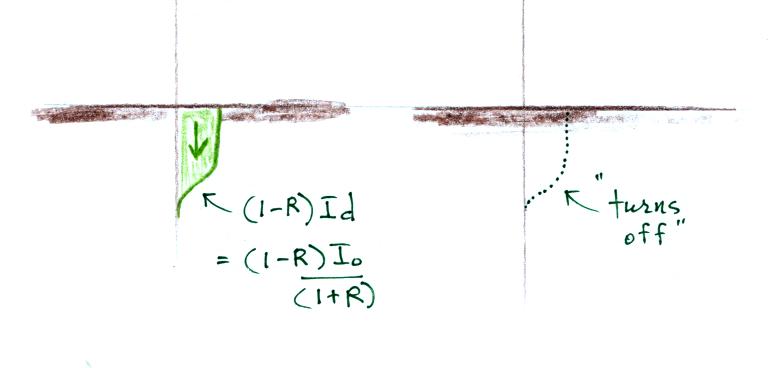

The unreflected current
doesn't
just travel down into the ground as shown in the earlier figure.
It probably spreads out horizontally. In any event, as a field
emitter, it "turns off" and stops radiating (it is
traveling into a conductor). So we need to subtract its
contribution to the total E field.

So the descent from peak field to a shoulder field
occurs when the
downward current wave reaches the ground. A portion of the
downward current stops radiating field.
Let's go back to our summary of the results of the experimental test of the transmission line model.

Much better agreement between transmission line model derived velocities and measured velocities was obtained when the Eshoulder amplitude was used instead of Epeak in the transmission line model equation together with Ipeak. This is particularly true for the 1987 experiment with its simpler launch platform. Keep the 1.51 x 108 m/s velocity value in mind, we'll being referring to it again shortly in the final section in today's notes.
We should note that we still haven't explained why a different vTLM was obtained when using dE/dt and dI/dt data.
We'll end this lecture with a look at some experimental measurements of distant electric radiation fields and estimates of peak I and peak dI/dt values that were derived from them. The measurements are described in the publication cited below.
"Submicrosecond fields radiated during the onset of first return strokes in cloud-to-ground lightning," E.P. Krider, C. Leteinturier, and J.C. Willett, J. Geophys. Res., 101, 1589-1597, 1996.
Here are some important points regarding this experiment.
1. Electric fields from lightning first return strokes 25 to 45 km away were measured. Only the radiation field component is present at these ranges. Propagation between the strike point and the recording station was entirely over salt water so that high frequency signal content was largely preserved. The recording station was actually one of the stations used in the triggered lightning experiment described above (Point 2 on the map at the start of today's lecture)
2. The recording instumentation was triggered on an RF signal rather than on E or dE/dt to prevent trigger bias.
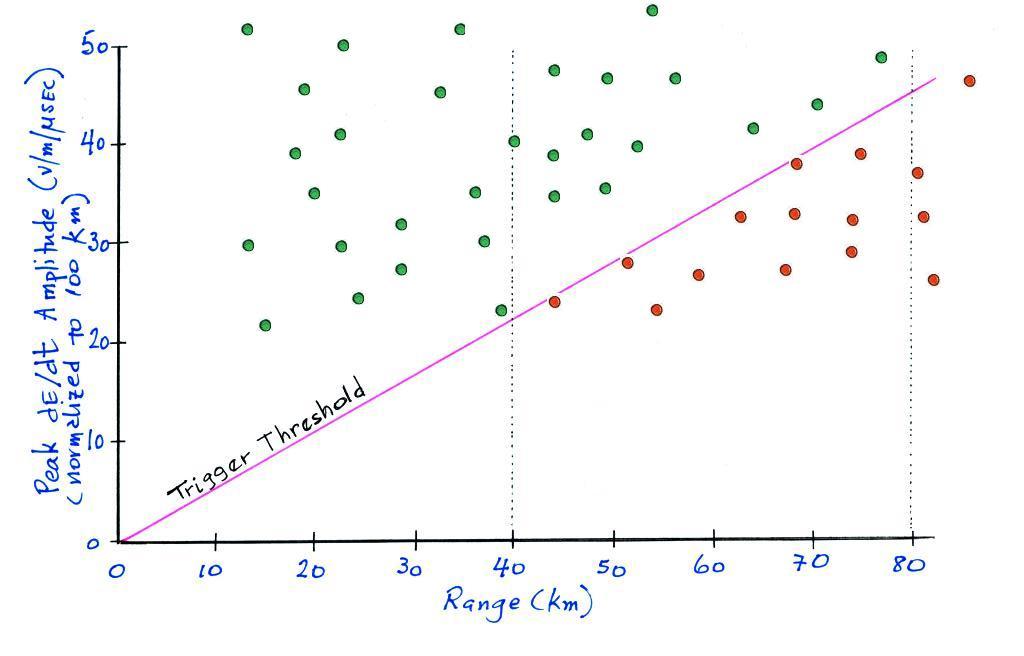
The plot above shows range normalized dE/dt data versus range. A set trigger threshold on an oscilloscope or waveform recorder of some kind, a fixed voltage, will correspond to larger and larger dE/dt values with increasing range. Between about 40 and 80 km the distribution of measured dE/dt signals will be biased toward larger signal amplitudes. Only the green points on the plot above which are above the trigger threshold would be recorded, beyond about 80 km very few of the dE/dt signals wwould be large enough to trigger the recording instrumentation. (This is a realistic but fictitious data set being used for illustration).
The histograms below show the effect of trigger level bias on the distribution of range normalized dE/dt measurements. The first histogram plots the range normalized dE/dt measurements between 40 and 80 km which triggered the recording system. The mean value was 44 V/(m μsec).
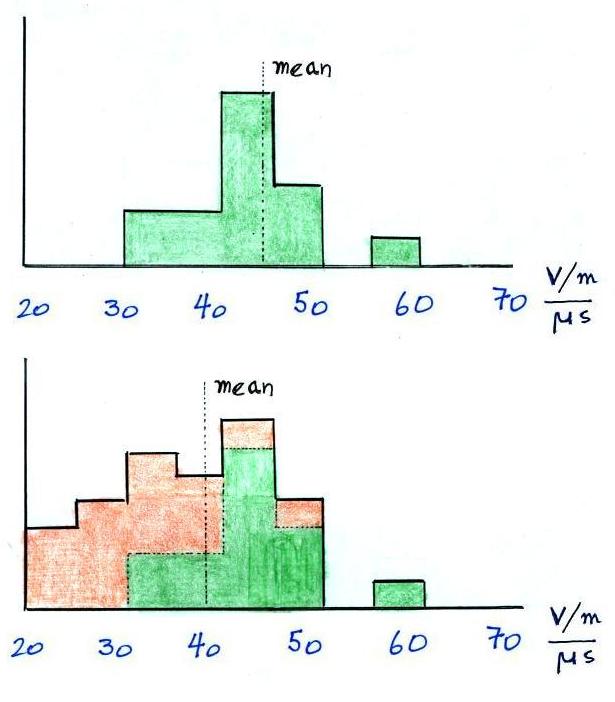
The bottom histogram is the true distribution. I.e. it includes the data that triggered the recording system and those that did not. Including the latter group of data lowers the mean to 38 V/(m μsec).
The table below illustrates how measured dE/dt values can be range normalized.

Three typical peak dE/dt values from return strokes at
ranges of
25, 35, and 65 km are shown in the left most column. We assume
the signals vary as 1/range. Data range normalized to 100 km are
shown in the right column.
3. Even though E field propagation was over salt water some high frequency attentuation was still present. An atttempt was made to correct for this.
The figure below shows the effects of propagation. The dI/dt waveform used in the calculations is shown at the top of the figure.
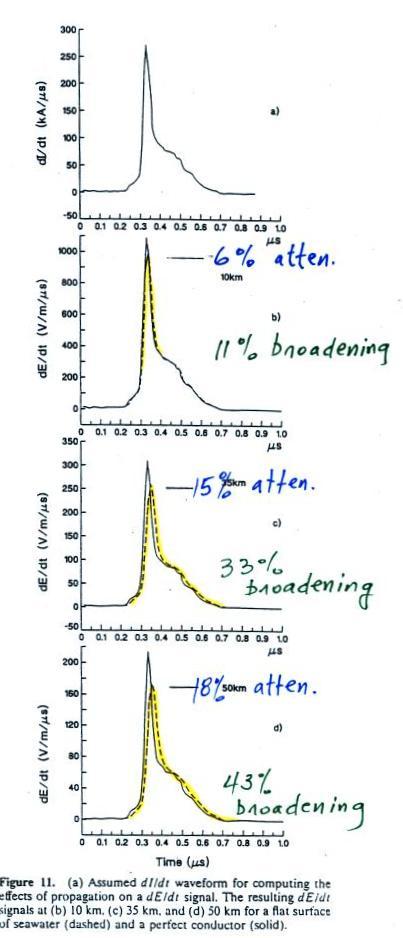
The three lower plots show the dE/dt signal at 10, 35, and 50 km range. The signals are both attentuated and broadened (the percentage refer to the pulse width at half maximum). The solid line shows propagation over a perfectly conducting surface for comparison.
And here are the main results from the experiment. First the estimate of peak I derived from measured E amplitudes using the transmission line model expression.

Note the value of the velocity used in the calculation is the best fit between measured I and E values in the experimental test of the transmission line discussed earlier in today's class.
Next the estimate of peak dI/dt

Again the velocity from the experimental test of the
transmission
line model was used. Note the value used for dI/dt is different
from the value used to estimate peak I.
The estimate of average peak current compares well with values from measurements made during strikes to instrumented towers that were summarized in an earlier lecture. Those tower measurements probably did not have sufficient time resolution to accurately record peak dI/dt values. So the measurement above is one of the best estimates of peak dI/dt in first return strokes available in the literature.

Let's go back to our summary of the results of the experimental test of the transmission line model.

Much better agreement between transmission line model derived velocities and measured velocities was obtained when the Eshoulder amplitude was used instead of Epeak in the transmission line model equation together with Ipeak. This is particularly true for the 1987 experiment with its simpler launch platform. Keep the 1.51 x 108 m/s velocity value in mind, we'll being referring to it again shortly in the final section in today's notes.
We should note that we still haven't explained why a different vTLM was obtained when using dE/dt and dI/dt data.
We'll end this lecture with a look at some experimental measurements of distant electric radiation fields and estimates of peak I and peak dI/dt values that were derived from them. The measurements are described in the publication cited below.
"Submicrosecond fields radiated during the onset of first return strokes in cloud-to-ground lightning," E.P. Krider, C. Leteinturier, and J.C. Willett, J. Geophys. Res., 101, 1589-1597, 1996.
Here are some important points regarding this experiment.
1. Electric fields from lightning first return strokes 25 to 45 km away were measured. Only the radiation field component is present at these ranges. Propagation between the strike point and the recording station was entirely over salt water so that high frequency signal content was largely preserved. The recording station was actually one of the stations used in the triggered lightning experiment described above (Point 2 on the map at the start of today's lecture)
2. The recording instumentation was triggered on an RF signal rather than on E or dE/dt to prevent trigger bias.

The plot above shows range normalized dE/dt data versus range. A set trigger threshold on an oscilloscope or waveform recorder of some kind, a fixed voltage, will correspond to larger and larger dE/dt values with increasing range. Between about 40 and 80 km the distribution of measured dE/dt signals will be biased toward larger signal amplitudes. Only the green points on the plot above which are above the trigger threshold would be recorded, beyond about 80 km very few of the dE/dt signals wwould be large enough to trigger the recording instrumentation. (This is a realistic but fictitious data set being used for illustration).
The histograms below show the effect of trigger level bias on the distribution of range normalized dE/dt measurements. The first histogram plots the range normalized dE/dt measurements between 40 and 80 km which triggered the recording system. The mean value was 44 V/(m μsec).

The bottom histogram is the true distribution. I.e. it includes the data that triggered the recording system and those that did not. Including the latter group of data lowers the mean to 38 V/(m μsec).
The table below illustrates how measured dE/dt values can be range normalized.

3. Even though E field propagation was over salt water some high frequency attentuation was still present. An atttempt was made to correct for this.
The figure below shows the effects of propagation. The dI/dt waveform used in the calculations is shown at the top of the figure.

The three lower plots show the dE/dt signal at 10, 35, and 50 km range. The signals are both attentuated and broadened (the percentage refer to the pulse width at half maximum). The solid line shows propagation over a perfectly conducting surface for comparison.
And here are the main results from the experiment. First the estimate of peak I derived from measured E amplitudes using the transmission line model expression.

Note the value of the velocity used in the calculation is the best fit between measured I and E values in the experimental test of the transmission line discussed earlier in today's class.
Next the estimate of peak dI/dt

The estimate of average peak current compares well with values from measurements made during strikes to instrumented towers that were summarized in an earlier lecture. Those tower measurements probably did not have sufficient time resolution to accurately record peak dI/dt values. So the measurement above is one of the best estimates of peak dI/dt in first return strokes available in the literature.