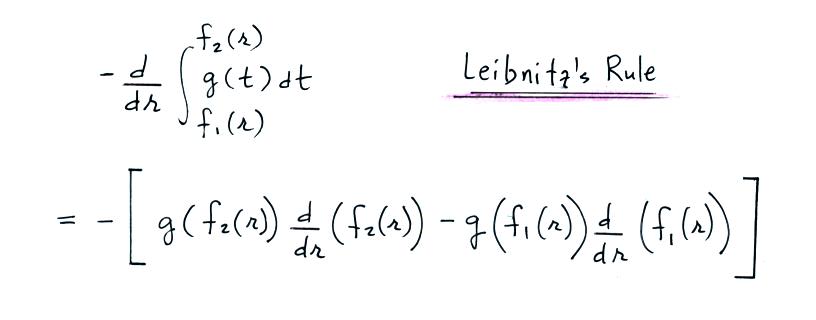We'll soon be discussing lightning protection in this class.  We'll look at how structures can be protected from lightning strikes and how you can prevent transients on power lines and signal cables from damaging sensitive electronics.  Before doing that we might ask how likely is it for a building or anobject to struck by lightning.  Today we are going to derive the "nearest neighbor" probability distribution function.  If lightning strikes are randomly distributed over a particular region we'll be able to use the nearest neighbor function to answer questions such as:

What is the most probable distance to the closest strike (the nearest neighbor)?

What is the average distance to the closest strike?

What are the chances that the closest strike is inside a distance R of a randomly chosen point on a map?

Before getting into the details of the nearest neighbor derivation it might be a good idea to review some basic concepts.

A probability distribution is defined above.  The function must be normalized so that integrating the function over all possible values of x (all possible outcomes) is 1.


The mean value of x is determined by multiplying x by its probability distribution function and integrating over all values of x.


The cumulative probability distribution function above gives you the chance that x is less than or equal to some value xo.  You could also compute the probability that x is equal to or greater than xo.

Here's an example.  We'll figure out the probability distribution function for points on a line segment of length L. 


Multiplying f(x) times dx will tell you what the chances are of falling between x and x+dx.  Note the odds of falling at a point x are zero because a single point has zero width.  We need to normalize the function f(x).

Now we can calculate the average value of x.


Here's a second example, sort of a 2-dimensional version of what we looked at earlier.  We'll make use of this when we derive the nearest neighbor function.


What is the probability that a randomly chosen point will fall between r and r + dr on a circle of radius R.  We assume the all points on the circle are equally likely (that's why f(r) is set equal to a constant k).  This is sort of like throwing darts at a dart board (with the requirement that the dart must hit the dart board). 

We need to normalize the distribution function.

So the probability that a dart thrown at a dartboard will land between r and r + dr is

what if we were to throw N darts?  As long as the throws are independent of each other, the chances of having a dart land between r and r + dr would be N times the result above

We can also compute the average r just like we did in the earlier problem


Now we're ready to derive the nearest neighbor probability distribution function.  The situation is illustrated in the figure below.

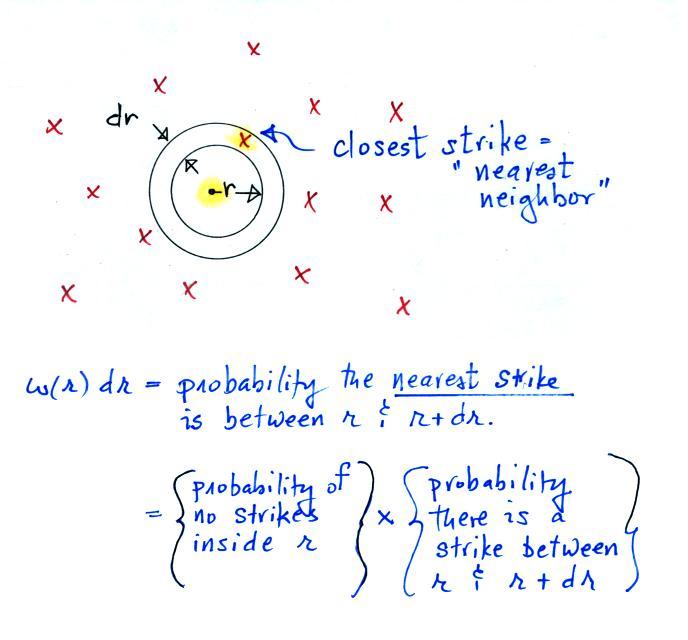
We're asking - what is the probability that the nearest strike is between r and r+dr from a randomly chosen point (in the figure above the randomly choisen point is the highlighted point in the center of the circle)?  This is not quite the same as asking what the chances are of falling between r and r + dr because now we want a strike between r and r + dr but nothing inside of r.  We'll use w(r) to denote this "nearest neighbor" probability distribution function.

We'll assume a lightning strike density of Ng strikes per square kilometer per year and we assume that the strikes are randomly distributed.  So we can write w(r) as follows.

At (1) we are integrating w(r) from 0 to r to find out the probability that the nearest neighbor is inside r.  To find the probability that the nearest neighbor isn't inside r we subtract the integral from 1.  That's expression (2) in the equation above.  (3) is the probability that a strike falls between r and r + dr.  It's really just the dart board question again.  We're multiplying by Ng because there are, on average, Ng strikes per km2 per year.

The area term in the denominator of the dart board expression is really just built in to Ng.  Ng is a density: strikes per square kilometer.

How do you solve the equation above for w(r) when w(r) appears in an integral?  The first step is to differentiate the equation with respect to r.

At this point, we'll need to take a short detour.  We need to differentiate the integral term with respect to r, but r appears in one of the integral's limits. 

Leibnitz's rule shows you how to handle the circled term.

The equation above is one version of Leibnitz's rule.  In the equation below, we apply it to our particular problem.
 



Now we'll go back and substitute this into Eqn. 1 above. 



Do you see what was done with the last term in the first equation above?


We go back to an earlier expressure and divide w(r) dr by term (3) above and use that to replace term (2). 
Now back to where we left off.


This is now in a form that we can solve


We have an expression for w(r) but it contains an unknown constant k.  But once we normalize this equation we'll be able to determine a value for k.


The last equation (highlighted in yellow) is the nearest neighbor distribution function.




The data above (from the National Lightning Detection Network) shows 24,790 cloud to ground strikes in a 51 km by 51 km area centered on the Main Gate at the U of A.  These strikes occurred between Jan. 1, 2000 and Sept. 23, 2002, a nearly 3 year period.  One thing to notice is that the points appear to be pretty uniformly distributed.  We can use this data to estimate the CG flash area strike density.


This figure shows how that is done.  We multiply 24790 by 1/0.7 to correct for the 70% detection efficiency of the lightning locating network.  We then multiply by 1.45, the average number of strike points per flash (see the figure below).  We divide by the 51 km x 51 km area and divide by 3 years (there is very little lightning between Sept. 23 and Dec. 31).  On average there are 6.6 strikes per square kilometer per year in the Tucson area.


This is a portion of a figure that appeared in Lecture 15.  The left most figure is where the average 1.45 strike points per flash value came from.