Much of this lecture and the next are adapted from material in Uman's The Art and Science of Lightning Protection (Cambridge Univ. Press, 2008; paperback version 2010).  An interesting survey of the costs of various types of lightning damage can be found on the first 3 or 4 pages in Chapter 2.  Here are are few examples of the interesting facts and statistics found there:

The 1977 lightning-caused power blackout in New York City cost about $350 million.  30% of all power failures are due to lightning with an annual cost close to $1 billion.

Estimates of the costs of lightning damage to insurance companies range from 1/3 to $1 billion.  In total about 5% of insurance claims involve lightning (50% in Florida in the summer)

30,000 house fires are caused every year by lightning.  About half of the 20,000 wildfires every year are caused by lightning.  The cost of fighting wildfires was about $1.5 billion in 2006 (a record year).

Lightning damage to commercial airlines costs ~$2 billion per year.  Damage to military aircraft is comparable.

Lightning causes damage to perhaps 100,000 computers/year.

The dimension of the house are roughly: 20 m long (l) by 12 meters wide (w).  The top of the pitched roof (h) is about 5 m high.  To determine the effective area we must extend the actual horizontal dimensions of the house by 2 times the height (2 x h) on all four sides of the house.

Then we multiply this area by the strike density from the last lecture.

You would need to question whether it is worth the expense of installing lightning protection (especially since I don't actually own the house).

You can do the same kind of calculation for a normal power distribution line.  We'll assume the arms on the power pole that hold the power lines are 5 m wide and are about 10 meters above the ground.  The effective area of 100 km of line then would be

 

In this case some lightning protection is probably advisable.  Often a ground wire will be run above the current carrying wires.  Lightning then will hopefully strike the ground wire (and be safely carried to ground) instead of the current carrying wires.

Protection system components
Lightning protection for a house or building usually consists of 3 components: an air terminal (lightning rod or Franklin rod), a down conductor, and grounding.

Dimension A in both figures is 20 or 25 feet and is the maximum spacing recommended by the NFPA between lightning rods.  Dimension B in the lower figure is 20 feet and is the maximum spacing between rods located along the edge of the roof.  Two down conductors at opposite corners of the roof are shown in the top figure.  The bottom figure has a down conductor at each of the buildings corners.

For structures less than 50 feet tall

Aa lightning rod provides a 45^o or 60^o cone of protection.  The 45^o cone from a single lightning rod is shown at top in the figure below.

A larger structure can be protected with multiple rods with overlapping zones of protection.

A different approach is used for larger structures.  We need to recall that the striking distance, d,  is the distance between the leader tip and the ground at the moment upper connecting discharges are initiated. The leader can potentially strike anything withing a distance d of the leader tip.

           
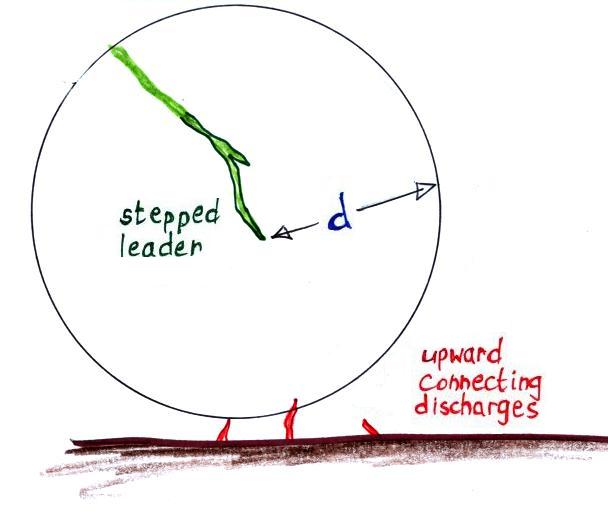
In the rolling sphere method, you imagine rolling a sphere of radius d (d is the striking distance) over the structure being evaluated for lightning vulnerability.  Parts of the building touched by the sphere are at risk; those parts of the building could be struck.  Portions that aren't touched are safe.

The height of the building at left is less than or equal to d.  The sides of the building aren't touched by the sphere, they've been shaded blue and are safe.  The sphere does touch the top of the building, it is vulnerable.  Lightning protection would need to be installed on the roof.  The building at right is quite a bit higher than d.  Much of the sides as well as the roof can be struck by lightning.  Protection would need to be installed on the top sides of the building and the roof.  Fragments of building materials knocked off the sides of buildings by lightning are apparently a serious hazard to people on the street below.

Air terminals could be mounted on the top of a tall buildings.  Additionally, the building designers could make metal window shades and window frames part of the lightning protection system by connecting them to the down conductor.

Note the spacing of the air terminals must be such that the rolling sphere doesn't touch the roof in between adjacent lightning rods.

What value of d should be used?  Researchers have tried to relate the striking distance to the amplitude of the peak return stroke that follows.  Generally an expression of the form

is used.  An example curve is shown below

Protection of a roof

A roof can be protected by multiple lightning rods.  An old question is whether pointed rods or blunt rods work best.  Some recent research (a couple of recent studies:  "Measurements of Lightning Rod Responses to Nearby Strikes," C.B. Moore, G.D. Aulich, and W. Rison, Geophys. Res. Lett., 27, 1487-1490, 2000 and "Lightning Rod Improvement Studies," C.B. Moore, W. Rison, J. Mathis, G. Aulich, J. Appl. Meteorol., 39, 593-609, 2000  ) suggest that the blunt rods might be more effective.  The NFPA allows either type to be used.  Rods should be at least 10 inches tall.

So called "unconventional" rods that use radioactivity or high voltage to try to initiate an "earlier" upward connecting discharge are generally not thought to be any more effective than conventional "Franklin" rods.

A wire mesh covering the roof of a building or vulnerable installation on the ground can be used instead of lightning rods.  A wire mesh covered the administration trailer at the rocket triggered lightning site in Florida for example.

The following table gives recommendations for the spacing of the wires in a wire mesh (based on Table 4.2 in Uman's "The Art and Science of Lightning Protection")

Air terminals should be connected to as many down conductors as possible.  Lightning rods on a house should be connected to at least two down conductors (at opposite corners of the house for example).

 
There are several reasons for this:

(i)  The down conductor will have some resistance and impedance.  Connecting inductors or resistors in parallel reduces the combined impedance.

(ii) The B fields from two down conductors positioned on opposite sides of a building will point in opposite directions in the interior of the building.  This will reduce the strength of the B fields inside the structure and reduce the intensity of voltages and currents induced in electronic circuits inside the building.

The recommended minimum crossectional area for down conductors is about 50 mm² for copper  (that correcponds to a radius of 4 mm, a diameter of 8 mm or roughly 1/3 inch)

Almost closed loops on the down conductor should be avoided.  This adds impedance and sparks are likely to jump across adjacent points on the down conductor.

Rather than going around a protrusion on a building wall, it would be better to go through the protrusion and keep the down conductor as straight as possible.

If a lightning protection system is struck it can easily rise to a potential of a few megavolts (see the discussion at the beginning of Lecture 16).  The down conductor should be "bonded" to (electrically connected to) metallic objects within about 5 m to prevent sparking from the down conductor to nearby metallic objects.  In the figure below (my rental house again) the down conductor has been connected to a water faucet at (1), to a vent pipe at (2), and to an evaporative cooler at (3).  A second down conductor extends from the roof to ground at Point 4.

3 x 10⁶ V/m is need to breakdown air at sea level
500 kV/m is the average field needed for propagation of negative polarity leaders
300 kV/m is the average field needed for positive leader propagation.

Grounding
Grounding rods are generally copper clad steel and should be at least 8 feet long.  The bottom end should be at least 10 feet deep.

Grounding can be improved by connecting grounding rods to a counterpoise, a loop of grounding wire that encircles the structure.  This reduces potential differences inside the loop.

The grounding can be also be connected to a buried mesh under the structure or to interconnected rebar in the concrete base of the structure.  This is well illustrated in an article by V.A. Rakov "Lightning Protection of Structures and Personal Safety."

Here is a table of resistivities of various materials (Table 5.1 in Uman's "The Art and Science of Lightning Protection").

Material	Resistiviy in ohm-meters
ocean water	0.1 - 0.5
ground, well & spring water	10 - 150
lake & river water	100 - 400
rain water	800 - 1300
commercial distilled water	1000 - 4000
chemically clean water	250000
clay	25 - 70
sandy clay	40 - 300
peat, marsh & cultivated soil	50 - 250
sand	1000 -3000
moraine	1000 - 10000
ose (calcereous remains)	3000 - 30000