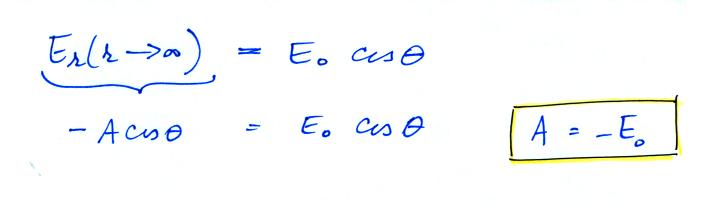In our last lecture we looked at a 20 minute long electric field recorded at the ground.  It showed a change from fair weather conditions with fields of about 200 V/m to stormy weather where fields were at least 10 times more intense and of the opposite polarity.  Superimposed on the field record were abrupt field changes produced by lightning discharges. 

A lightning discharge usually takes place in less than a second and there are some lightning processes that occur on microsecond and submicrosecond time scales.  The figure below illustrates this.  An electric field mill can't resolve all the field changes and variations that occur on this time scale.  Don't worry about the details on this figure at this point; we'll have a detailed look at the processes that occur during a cloud-to-ground discharge later in the semester.



One way of measuring these faster time varying electric fields is to use a flat plate antenna (aka flush plate dipole antenna).  It basically consists of a large flat grounded plate that would be positioned on the ground (preferably flush with the surrounding ground).  A smaller circular sensor plate is found inside a center hole as shown in the photograph below (the antenna is on the classroom floor in this photograph).




We look under the top plate of the antenna in the next picture.



The center sensor plate is supported by insulating nylon or teflon spacers.  The top end of the supports are covered with "rain hats" to try to keep the insulators dry during rainy weather.  A wire connection to the center plate connects to a BNC cable to carry the signal to processing and recording equipment.

In some ways the operation of this antenna is similar to the field mill.  In this case a time varying E field causes current to flow to and from the center sensor plate (you don't need to repeatedly cover and uncover the sensor plate).

This current is proportional to the time derivative of the electric field (σ in the equation below is the surface charge density on the sensor plate). 

Integrating the current gives an output signal that is proportional to E.


In the circuit above the antenna is connected to a capacitor, this is a passive integrator.  Some kind of measuring device would then be connected across the capacitor.



In some cases the input impedance of the measuring device together with a small capacitance in the passive integrator (a small capacitance would provide higher gain) gives a time decay constant that is too short (the time constant should be several times larger than the field variations that you are measuring).  It should be remembered also that there will be some capacitance between the center antenna plate and the surrounding, grounded plate (usually a few pF).

There are situations, though, where a passive integrator circuit might be suitable.


A triggered lightning discharge at 100 meters range will produce a much larger E field change signal.  You could make the integrating capacitor larger (with a correspondingly longer decay time constant) because you wouldn't need as much gain.   Actually you would probably also need to reduce the area of the antenna plate so as to not have too large an output signal.  In the case of triggered lightning, signals from antennas and other sensors are generally carried into a shielded metal trailer on fiber optics cables for safety reasons and to avoid noise pickup on the signal cables.

While a passive integrator is sometimes appropriate, it is more common to connect the flat plate antenna to an active integrator circuit like shown below.



When the E field antenna sensor plate is connected to an active integrator circuit like shown above, the input impedance of the measuring equipment won't affect the decay time constant.  The decay time constant is determined by the R and C values in the operational amplifier feedback circuit.

We can now make clear the differences between "fast E" and "slow E" antenna systems.


A slow E field antenna is used to faithfully reproduce field changes from an entire lightning discharge.  Not just return stroke changes but also leader processes and continuing currents that might occur between return strokes.  Since a typical discharge lasts 0.5 to 1 second, the decay time constant must be several seconds long.   The field changes superimpose on each other and the gain must be adjusted to keep the entire signal onscale.

Charged precipitation will sometimes carry enough charge to the antenna plate to drive a slow E field signal off scale.  One solution is to invert the antenna as sketched below.  This is sometimes done with field mills also.


Fast E field antennas are used to examine portions of the discharge on a faster time scale.  You might record and display the fields produced by the return strokes on a microsecond time scale for example.

A shorter decay time constant is used so that the output signal can return to zero in between separate discharges.  The gain can be increased because you only need to keep signals from individual strokes rather than the entire discharge onscale.  A system with a fast decay time is affected less by charged rain.

Here are typical Fast E and Slow E integrator circuits.  The second circut, in particular, shows a technique used to get the long decay time constants used in slow E field antenna systems.

An electric field antenna that is not flush with the ground surface will distort the surrounding electric field.  This is an appropriate point to review a problem worked in most undergraduate electricity and magnetism courses (the notes that follow are based on a class handout prepared by Dr. E. Philip Krider).

Conducting Sphere in a Uniform Electric Field
   Notes on the distortion of an initially uniform electric field Eo by the presence of an uncharged conducting sphere.  The sphere distorts the field such that the field lines are everywhere normal to the surface of the conductor.  Choosing the origin of our coordinate system at the center of the sphere,
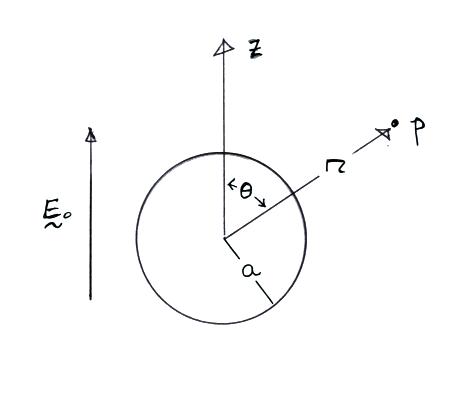
Spherical polar coordinates are used, there is azimuthal symmetry, so the potential and the electric field depend on r and θ  only.  We can proceed to solve Laplace's equation for the potential, Φ, subject to the boundary conditions that
 
In the spherical coordinate system


Assuming the variables are separable, we try a general solution of the form:

Just looking at the boundary condition (Eqn. (ii)), we simply try a T(θ) function of the form


Now, inserting this into our original differential equation, we find

click here to see some of the missing details.
Now, let's try a solution to the R equation of the form

When we substitute this into the differential equation above we get

Now a general R solution will be of the form


and

Where A and B must be determined from the boundary conditions.
Now,
applying boundary condition (ii) as r goes to infinity
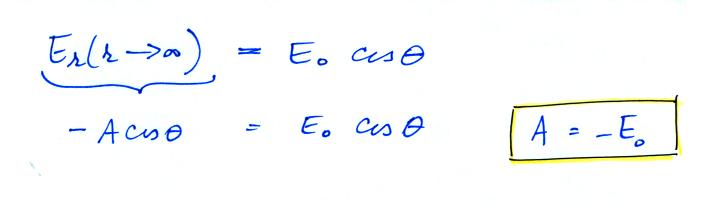
since



and our potential function is now



with this Φ our electric field components are:


and the surface charge density is


Note: The presence of the sphere increases the value of the ambient field at the top and bottom surface of the sphere by a factor of 3.
This figure gives you a rough idea of how the field is changed in the vicinity of the sphere.  E field lines must intersect the sphere perpendicularly. The field is enhanced (amplified) by a factor of three at the top and bottom of the sphere.
Enhancement of fields by conducting objects is an important concern.  In some cases (we'll look at an example or two later) the enhanced field is strong enough to initiate or trigger a lightning discharge.

The following handout gives a rough, back-of-the-envelope kind of estimate of the factor of enhancement.
This might require a little explanation.
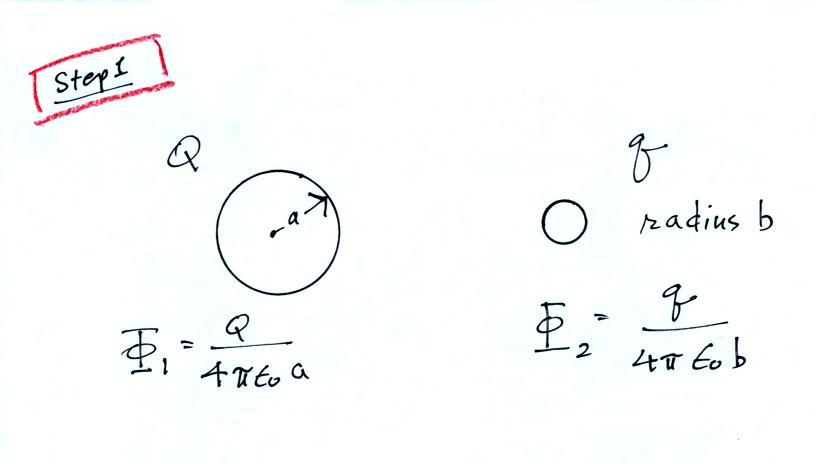
First you write down the potential at the surface of two conducting spheres of radius a and b, carrying charges Q and q (really just the potential a distance a or b from a point charge Q or q)
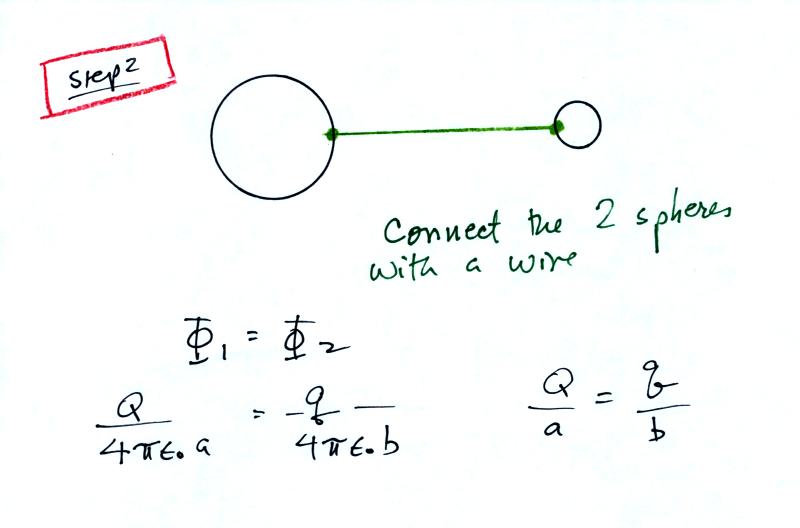
Then you connect the two spheres with a wire which forces the two potentials to be equal (this would of course cause the charge to rearrange themselves and turn this into a much more complex problem, but we will ignore that).
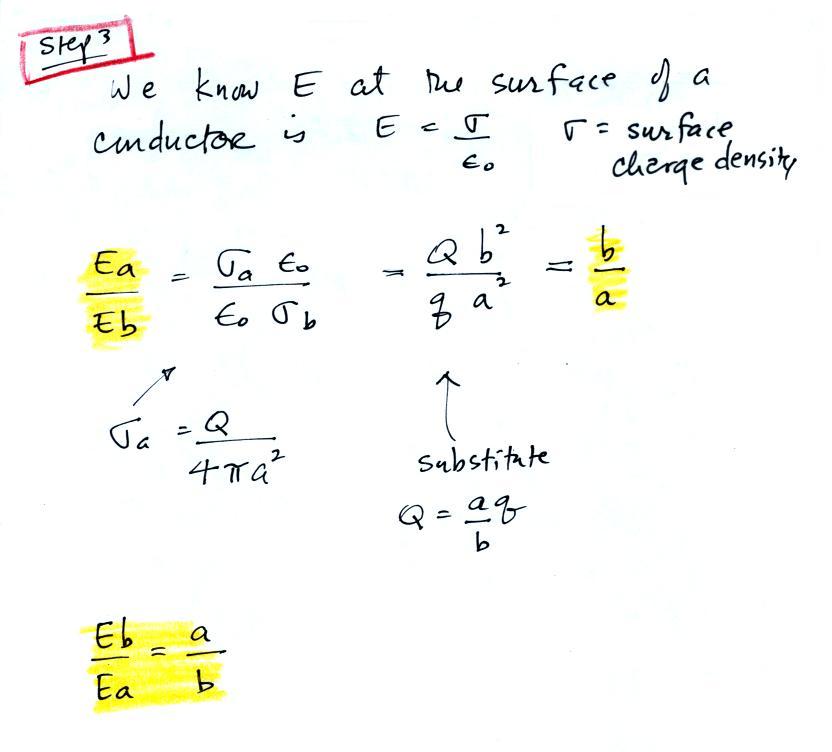
Finally we write down expressions for the relative strengths of the electric fields at the surfaces of the two spheres.  We see that the field at the surface of the smaller sphere is a/b times larger than the field at the surface of the bigger sphere.

Here is a real example of field enhancement that lead to triggering of a lightning strike and subsequent loss of a launch vehicle (you'll find the entire article here)


In this case the rocket body together with the exhaust plume created a long pointed conducting object.  Enhanced fields at the top and bottom triggered lightning.

Lighning is sometimes triggered at the tops of tall mountains

Note the direction of the branching.  This indicates that this discharge began with a leader process that traveled upward from the mountain.  Most cloud to ground lightning discharges begin with a leader that propagates from the cloud downward toward the ground.  We will of course look at the events that occur during lightning discharges in a lot more detail later in the semester.