Thursday, Feb. 7, 2013

click here to download today's notes in a more printer friendly format


We first need to finish up an example that we didn't have time for in our last class.  It deals with what happens along an air-cloud boundary where there is an abrupt change in conductivity.  

 

 


Conductivity inside a cloud is lower than in the air outside a cloud.  This is because the small ions attach to much larger and much less mobile cloud particles (water droplets or ice crystals).  The E field must become stronger inside the cloud so that the current density (the produce of conductivity and electric field) stays the same inside and outside the cloud.  We'll see that layers of charge build up on the top and bottom surfaces of the cloud. 

We'll try to estimate how much charge is necessary along the upper surface of the cloud layer.

We don't really know Ez.  The current density, Jz, on the other hand is constant with altitude and we assume we know how conductivity changes as you move across the cloud-air boundary.

We can integrate this equation

 

So we conclude a layer of positive charge builds up on the top edge of the cloud.  In a similar kind of way you could show that a layer of negative charge would build up on the bottom edge of the cloud.


The effect of these two layers of cloud is to intensify the field inside the cloud.  The product of higher field times lower conductivity inside the cloud is able to keep the current density equal to the current density outside the cloud.

Screening layers that form along the edges of a thunderstorm effectively mask the main charge centers inside the cloud.


One of the consequences of this is that it makes it difficult to use measurements of E field at the ground to estimate how much charge builds up in the main charge centers inside the cloud.  We will find that if you use sudden abrupt changes in electric field,  ΔE measurements,  you can determine the amount and location of charge neutralized during lightning discharges.  The abrupt field change occurs quickly enough that there isn't sufficient time for the charge screening layers to rearrange themselves and mask the field change.


The next several figures show measurements of fair weather conductivity, electric field, and current density made during a field experiment in 1978 in Wyoming.  Simultaneous measurements were made with a variety of different instruments from different research groups.  Instruments were carried up to about 30 km altitude by balloon and measurements were made on the ascent and often during the descent.  Here's a link to the full article (pdf file).

The list below gives you an idea of the electrical parameters that were measured and the various types of sensors that were used.

 

Measurements of conductivity versus altitude made on two different days are shown in two graphs below.

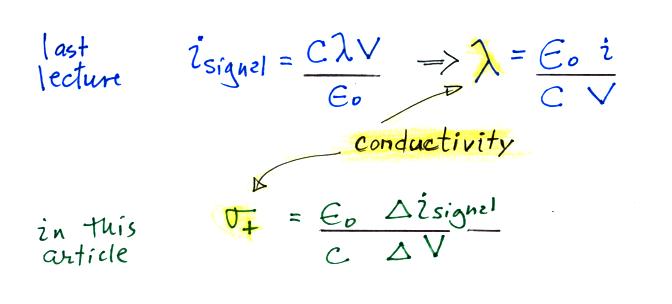
Conductivity values range from about 5 x 10-14 mhos/m at 2 km or so above the ground to about 1000 times higher near 30 km.  The conductivity values are from just the positively charged small ions.  The notation "GC" in the figure refers to "Gerdien Condenser."  The cylindrical capacitor discussed in the last lecture would be an example of a Gerdien condenser type instrument.  Conductivity was estimated using the Isignal/V slope method described in our last lecture (σ is used in the article instead of λ).


All of the measurements are in good agreement with the exccption of the relaxation time method.  This is just the decay time constant we derived in a previous lecture.

 

A second set of conductivity measurements.  These include both positive and negative small ions.

 

The next two plots show measurements of electric field versus altitude.



E field values decrease from a few 10s of volts/meter 2 or 3 km above the ground to less than 1 V/m near 30 km (note: the x-axis values are, from left to right, 0.1, 1.0, 10 and 100 V/m).

 

The next plot shows the vertical profile of current density, Jz.  Measurements from two different days are plotted together.


Note first of all that current density does stays fairly constant with altitude something we expect under steady state conditions (the x-axis labels, from left to right, are 0.1, 1.0 and 10 pA/m2).  The yellow curve is the product of electric field and positive small ion conductivity, not a measurement of Jz.  You would expect the measured Jz (which includes both positive and negative charge carriers) to to be roughly twice the positive conductivity times electric field, but it isn't.  The apparent explanation for this descrepancy is shown below (though this seems like too simple a mistake for the researchers to have made):


One of the Jz sensors consisted of two conducting hemispheres insulated from each other.  Charge is induced on the two hemispheres by the ambient electric field.  The figure above shows that the sensor is only capturing half of the charge carries in the atmosphere and therefore only measuring half of the current density, Jz.  There might also be some uncertainty about the effective crossectional area (collection area) of the current sensor.

The problem appears to have been corrected in the plot below which is a reanalysis of the Wyoming data.  The plotted points are conductivity (positive and negative polarity) times measured electric field.  The plotted values cluster around a value of about 2.5 pA/m2 (note again how uniform Jz is with altitude).  Measured Jz was about twice this, about 5.1 pA/m2.


The next graph summarizes measurements from a different field experiment conducted in the North Atlantic ocean.

The plot shows vertical profiles of E field (highlighted in blue), measured positive and negative conductivities (green), and the calculated current density (in yellow, the product of positive and negative conductivity and measured electric field).  The calculated current density values are clustered around 1.25 pA/m2, the measured total current density was about twice that, 2.35 pA/m2.


Both figures are from W. Gringel, J.M. Rosen, ande D.J. Hofmann, "Electrical Structure from 0 to 30 km Kilometers," Ch. 12 in The Earth's Electrical Environment, National Academy Press, 1986. (available online at www.nap.edu/books/0309036801/html/)


Now the main part of today's class, we'll start to look at how small ions are created.  Small ions are the mobile charge carriers that give the atmosphere it's conductivity.  First something must ionize air molecules

 


Then water vapor molecules cluster around the ions to create "small ions."  Water molecules have a dipole structure as shown below. 


The oxygen atom carries excess negative charge and the hydrogen atoms positive charge.  Because of this the water vapor molecules orient themselves differently around the oxygen and nitrogen ions.  Conceptually this would look like

More water vapor molecules are able to surround the positive ions so they are bigger and have slightly lower electrical mobility than the negative small ions.


The next figure summarizes the processes that ionize air.

Radioactive materials in the ground emit alpha and beta particles, and gamma rays.  Alpha particles (i.e. a helium nucleus consisting two protons and two neutrons) are a strong source of ionization but only in the first few cm above the ground.  Beta particles (electrons) ionize air in a layer a few meters thick.  The effects of gamma radiation extend of 100s of meters.  Cosmic rays are the dominant source of ionization everywhere over the ocean and above 1 km over land.

The table below, not shown in class, gives an idea of how far these different types of radiation can travel above the ground and also typical ionization rates (ip stands for "ion pairs"). (from Chapter 11 in "The Earth's Electrical Environment," National Academy of Sciences, 1986  )

emission type

range of travel

ionization rate [ ip/(cm3 sec) ]

alpha particles

only a few cm above the ground

not well known

beta particles

a few meters above the ground

0.1 to 10

gamma rays

100s of meters above the ground

1 to 6

radon

depends on atmospheric conditions

1 to 20 at 1-2 m above ground

cosmic rays

1 to 2 ip/(cm3 sec) near the ground

 


In addition to being a source of atmospheric ionization, radon is a signficant health hazard and is the 2nd leading cause of lung cancer after cigarettes.  Here are links to articles concerning radon from the World Health Organization, Wikipedia, and the Environmental Protection Agency.

The following table shows a portion of the decay series that ultimately yield isotopes of radon.

                 



all of the Neptunium in the soil has decayed away..


Rn-222, Rn-219,
and & Rn-220
are sometimes
referred to as
"radon", "actinon",
and "thoron" respectively.
All three are also
known as
"emanatium."

 

 

Because of its relatively short half life compared to the age of the earth, all the Neptunium in the ground has decayed away.  Two isotopes of radon (Rn-222 and Rn-220) have half lives long enough to be able to diffuse out of the soil and into the air.

The article from the World Health Organization gives a typical outdoor radon concentration of 5 to 15 Becquerels/m3 (Bq/m3  -  1 Becquerel is one disintegration per second ).  We can do a calculation to see what this implies in terms of radon concentration and ion pair production rate.

The rate at which a radioactive material decays is described by the following equation

(so far in this course we have used λ to represent linear charge density, atmospheric conductivity, and now decay constant). 

We can solve the equation above to give

It is easy to relate the half life, t1/2, and the decay constant λ

The Rn-222 isotope has a half-life of 3.8 days.


Now that we know the decay constant we'll substitute back into the decay rate equation to determine the radon concentration needed to produce an average outdoors decay rate of 10 Bq/m3.


(the number density for air, 2.67 x 1019 air molecules/cm3 is sometimes known as Loschmidt's number). 

This is as far as we got in class but I'll finish the section so that it will all be in one place. 

We know the decay constant and now have a typical Rn concentration.  Next we can estimate the ionization rate caused by radon.  We need to know how much energy is contained by the α-particles emitted by radon and the energy needed to ionize air.


We can divide these two numbers to determine the number of ion pairs produced by each distintegration.  Then we multiply by the Rn concentration and the decay constant (which give the decay rate) to determine the ionization rate.


Radon gas decays into solid particles of polonium, lead, and bismuth.  The decay series is shown below (source):

These decay products can attach to dust particles which are then inhaled and trapped in the lungs.  Since the decay products are themselves radioactive, long term exposure can ultimately lead to lung cancer.  Radon is apparently the 2nd leading cause of lung cancer in the US after cigarette smoking and kills about 20,000 people per year.

Radon concentration indoors can build to levels that are much higher than normally found outdoors.  An extreme case is mentioned below.