
Today we will add two
additional small ion loss terms. A small ion can attach
to an uncharged particle, creating a charged particle or a
so-called "large ion".

Or a small ion of one polarity can attach to a charged particle of the opposite polarity creating an uncharged particle (provided the small ion and the particle have equal quantities of charge). These two new terms are included in the small ion balance equation below. The β+o and β+- terms are referred to as "attachment coefficients."
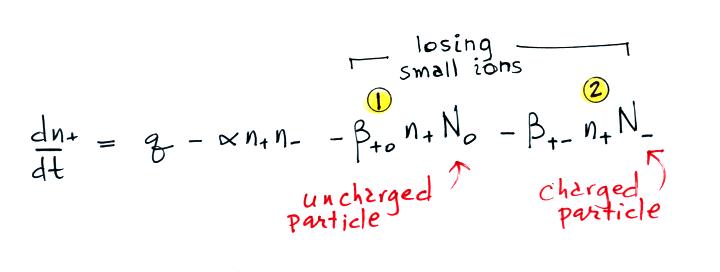

Or a small ion of one polarity can attach to a charged particle of the opposite polarity creating an uncharged particle (provided the small ion and the particle have equal quantities of charge). These two new terms are included in the small ion balance equation below. The β+o and β+- terms are referred to as "attachment coefficients."

We often assume that the
concentrations of positive and negative small ions and the
concentrations of positively and negatively charged
particles are equal. Let's also make the following
assumptions concerning the attachment coefficients.
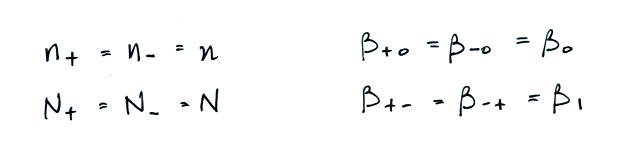
The balance equation then becomes
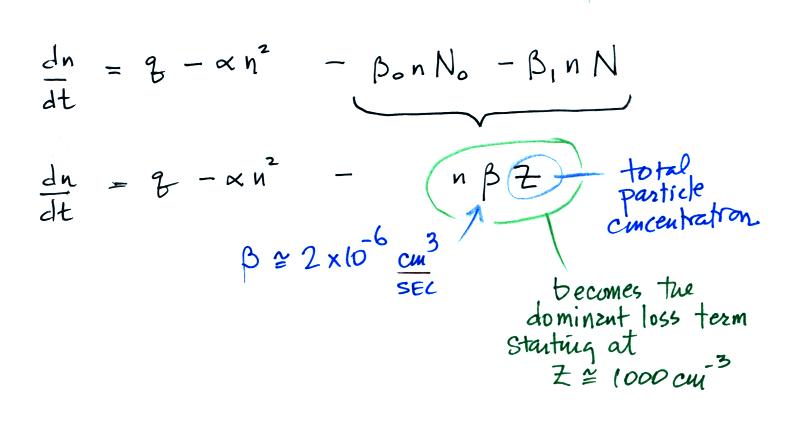
The bottom equation is just an additional
simplification of the top equation. A total particle
concentration term, Z, is used rather than keeping track
of the concentrations of charged and uncharged particles.
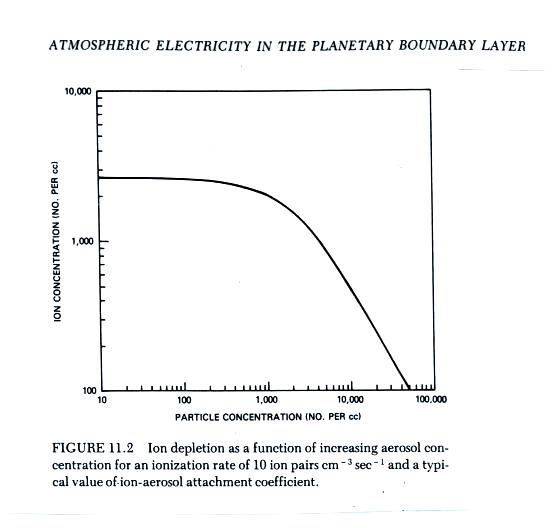
The figure below (from The Earth's Electrical Environment reference) illustrates how ion-particle attachment begins to significantly reduce small ion concentrations beginning at particles concentrations of about 1000 cm-3. Clean air typically has 100s of particles per cc while dirtier air would contain 1000s of particles per cc.
In some past editions of this course we have spent close to a full class period looking at how you might derive expressions for the ion-particle attachment coefficients. I'm not sure that's really necessary here. Though I have added supplementary notes that you can look at if you are interested. You can find them here. The first part of these supplementary notes deals with the attachment to uncharged particles, the second part considers attachment to charged particles.
We will spend some time considering what fraction of particles are uncharged and charged. We'll start with a large ion (charged particle) balance equation.
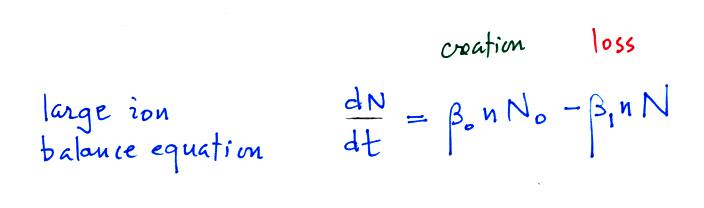
Now we'll look at the fraction of large and small particles that are uncharged. In some supplementary notes we look at how a relatively straight forward solution to the diffusion equation can be used to derive an expression for β0 . Then we consider the additional flux of small ions to a charged particle (diffusion plus the effect of the electric field created by the charged particle. That gives us an expression of β1 . At the end of those notes we see that β0 = β1 for large particles. We'll use that condition below

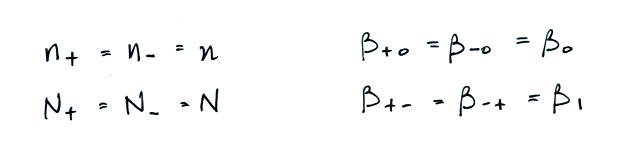

The figure below (from The Earth's Electrical Environment reference) illustrates how ion-particle attachment begins to significantly reduce small ion concentrations beginning at particles concentrations of about 1000 cm-3. Clean air typically has 100s of particles per cc while dirtier air would contain 1000s of particles per cc.

In some past editions of this course we have spent close to a full class period looking at how you might derive expressions for the ion-particle attachment coefficients. I'm not sure that's really necessary here. Though I have added supplementary notes that you can look at if you are interested. You can find them here. The first part of these supplementary notes deals with the attachment to uncharged particles, the second part considers attachment to charged particles.
We will spend some time considering what fraction of particles are uncharged and charged. We'll start with a large ion (charged particle) balance equation.
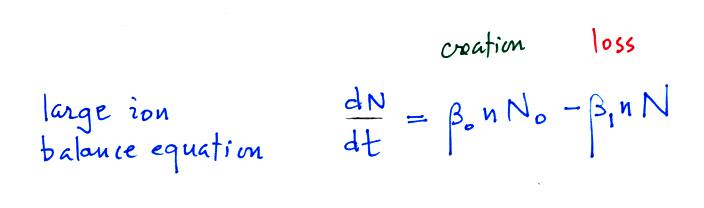
N in this equation can
represent the concentration of either positively or
negatively charged particles. Large ions are
created when a small ion attaches to an uncharged
particle. They are destroyed when a small ion
attaches to a charged particle of the opposite
polarity .
Under steady state conditions

Under steady state conditions

Now we'll look at the fraction of large and small particles that are uncharged. In some supplementary notes we look at how a relatively straight forward solution to the diffusion equation can be used to derive an expression for β0 . Then we consider the additional flux of small ions to a charged particle (diffusion plus the effect of the electric field created by the charged particle. That gives us an expression of β1 . At the end of those notes we see that β0 = β1 for large particles. We'll use that condition below

For large
particles you would expect to find equal numbers
of positively charged, negatively charged, and
non-charged particles.
For small particles
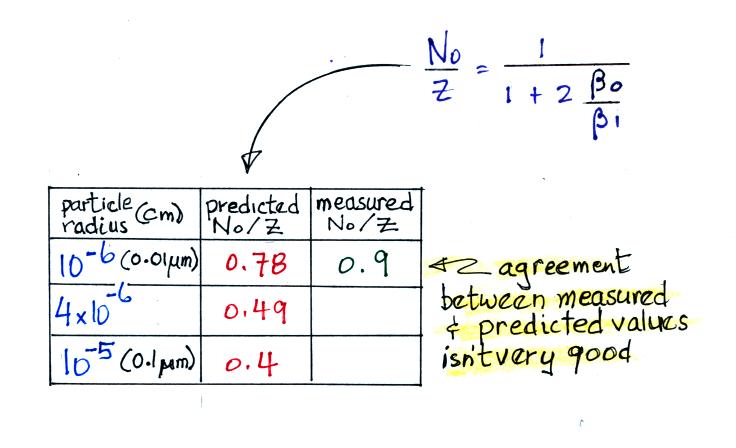
The agreement between predictions and measurements of the uncharged fraction (No/Z) is not very good for small particles. If the table had been extended to larger particles, the predicted No/Z would approach 0.33.
Better agreement is obtained using Boltzmann statistics.
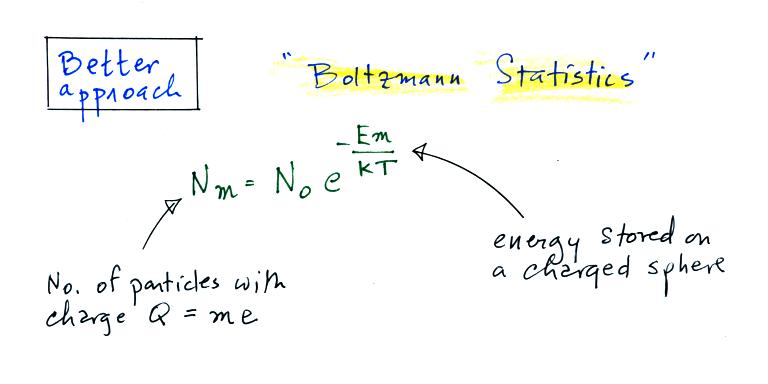
For small particles

The agreement between predictions and measurements of the uncharged fraction (No/Z) is not very good for small particles. If the table had been extended to larger particles, the predicted No/Z would approach 0.33.
Better agreement is obtained using Boltzmann statistics.

A charged
particle has a certain amount of "stored"
energy associated with it. Thus we can
use the Boltzmann distribution above to
predict the distribution of charged particles
(the particles can carry only integral
multiples of an electronic charge, i.e. Q =
me, where m is an integer and e is the charge
on an electron).
The energy stored on a charged sphere is (the details of the derivation are in a second set of supplementary notes)
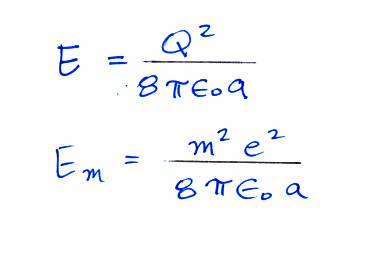
We can insert this expression into the
Boltzmann distribution equation above.
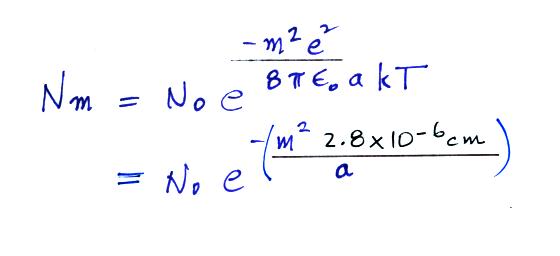
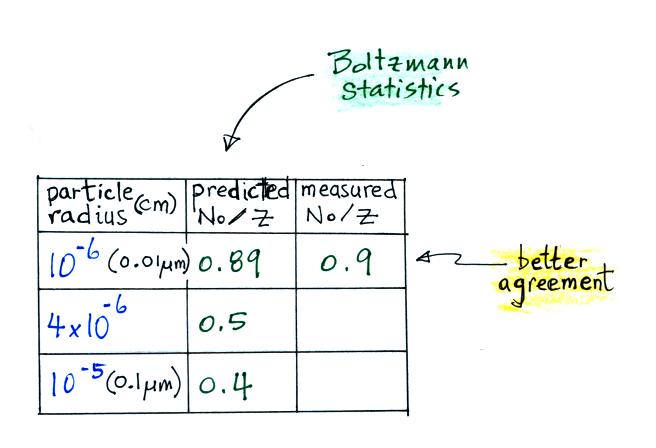
This agrees much better with the
measured value. The table shown earlier
is reproduced below. This time Boltzmann
statistics are used to predict the uncharged
fraction.
The energy stored on a charged sphere is (the details of the derivation are in a second set of supplementary notes)
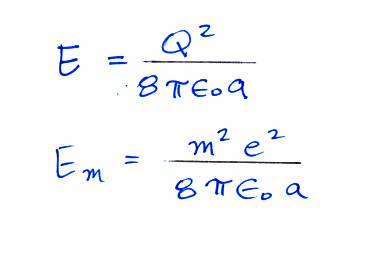
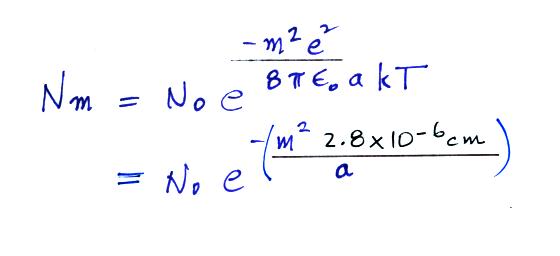
A temperature of
300 K was assumed in the calculation
above. The exponential starts to become
pretty small for particles with radii less
that 2.8 x 10-6
cm (especially if m > 1, that is the
particle has more than one electronic
charge). So we can see that most small
particles will be uncharged. Those that
are charged will mostly just carry 1
electronic charge. For example
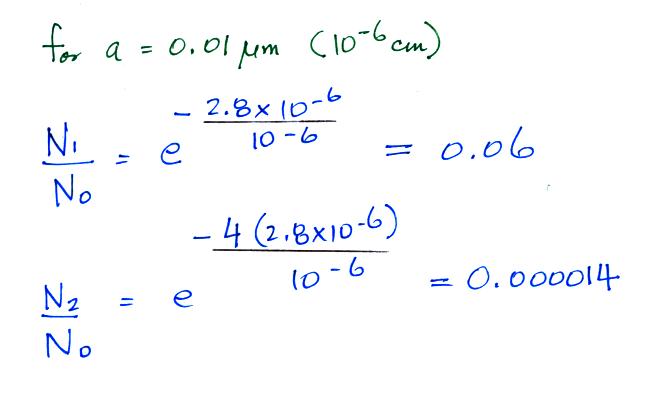
Now we can
compare predictions of the uncharged
fraction of particles with
measurements. Here are the details
of the predicted value for a particle with
radius = 10-6
cm.
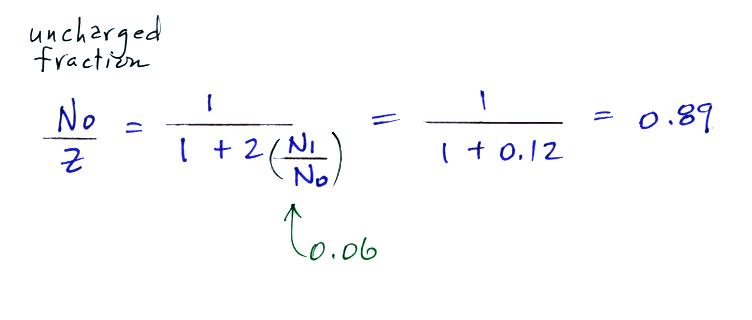
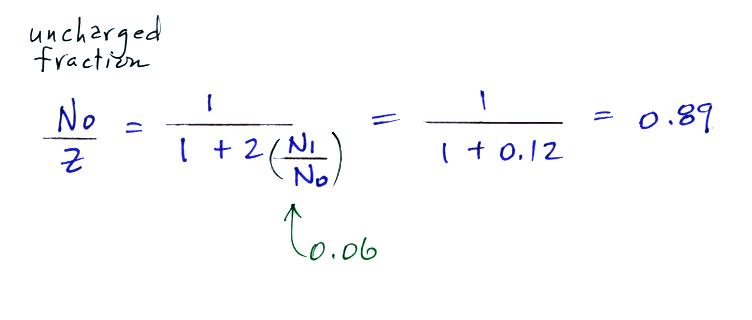

The agreement
between measured and predicted values is much
better. Again, if the table had been
extended to larger particles, we would expect
the predicted No/Z
to approach 0.33.