Newton's Law of Universal Gravitation


Isaac Newton is one of the greatest scientists that ever lived.  Among other things, he formulated a Law of Universal Gravitation that allows you to calculate the gravitational attraction between two objects.  With a little thought you can understand why certain variables appear in Newton's Law and why they appear in either the numerator (direct proportionality) or in the denominator (inverse proportionality).

You probably intuitively understand that the gravitational attraction between two objects (M and m in the figures) depends  on the distance between the objects.  The  gravitational force becomes weaker the further away the two objects are from each other.  The law of universal gravitation is actually an inverse square law, the gravitational attraction between two objects is inversely proportional to the square of the distance between the two objects.

If we think of M as being the mass of a planet and m the mass of its moon, we can see that the attraction between the two depends on the mass of the planet.  Jupiter exerts a stronger gravitational attraction on its moons than the earth.  M belongs in the numerator of Newton's equation.

In the figure below we consider two objects of different mass m on the surface of a planet.  The person with more mass (right figure below) weighs more than the person below with less mass (left figure).  So we do need to include m in the equation.

The complete formula is shown at the bottom of the page above.  G is a constant.  On the surface of the earth G, M, and don't change.  The gravitational acceleration, g, is just the quantity  [G times Mearth divided by ( Rearth )2 ].  To determine the weight (on the earth's surface) of an object with mass m you simply multiply m x g.  Incidentally g has values of 9.8 meter/sec2 (metric units) or 32 feet/sec2 (English units).

The figure below gives the Metric and English units of mass and weight.  You have probably heard of pounds, grams, and kilograms.  You might not have heard of dynes and Newtons.  Unless you've taken a physics course, you've probably never heard of slugs.


Let's take this a step or two further and stick in some typical numbers.  We'll assume a person has a mass of 70 kg (metric units) and a weight of 154 pounds (English units). 



Finally some explanation of why we call g the gravitational acceleration. 

You've probably heard of Newton's 2nd law of motion: Force = mass x acceleration (often abreviated F = m a).  If a force is exerted on an object the object will begin to move (in the direction of the force).  The object's speed will to increase (accelerate) as long as the force is applied.  Newton's law allows you to determine the acceleration, you simply divide the Force by the object's mass (the middle equation above). 

Gravity causes objects to fall and to speed up as they fall.  You can use Newton's 2nd law and the weight equation to determine the downward acceleration caused by gravity.  Note that the acceleration caused by gravity is the same regardless of mass.  An object with a large mass will accelerate at the same rate as an object with smaller mass.  This is true as long as gravity is the only force present.
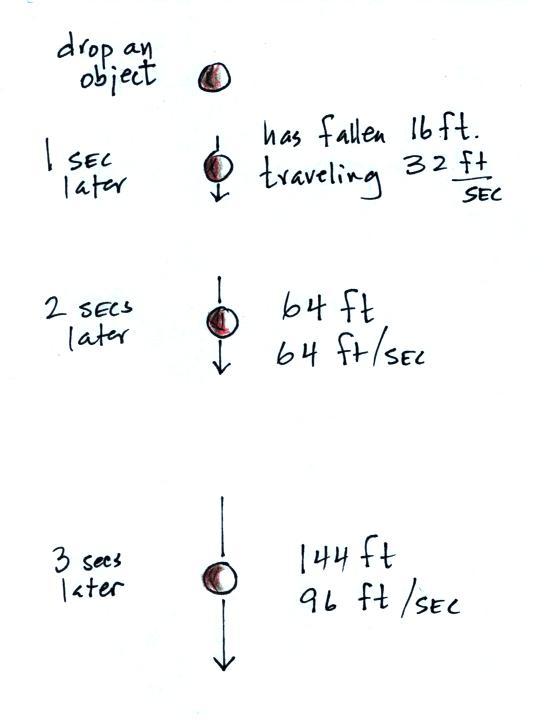
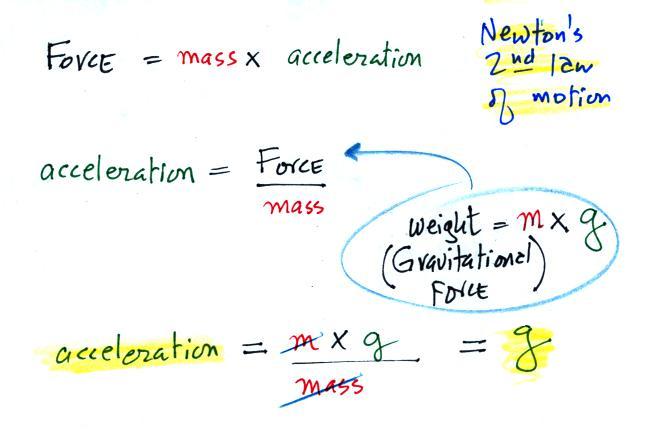
The gravitational acceleration has a value of 32 ft/sec in the English system of units (9.8 m/s).  We let the object in the figure below start to fall at time zero.  One second later it will have fallen 16 feet and will be moving at a speed of 32 feet per second (ft/sec).  In the next second it's speed will increase by 32 ft/sec and will now be falling at 64 ft/sec.  The same thing will happen in the second after that.  After three seconds the object will be falling 96 ft/sec and will have fallen 144 ft.