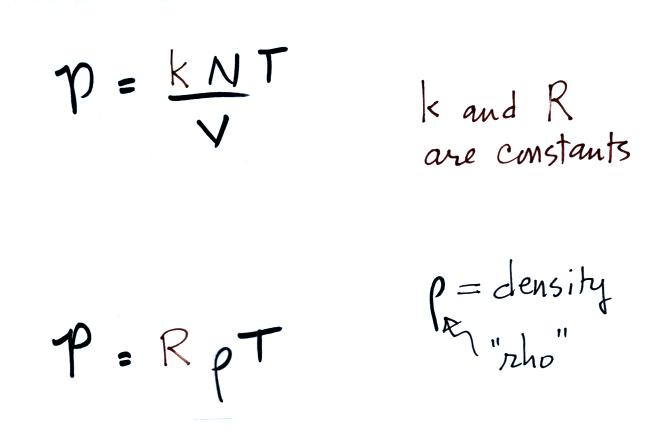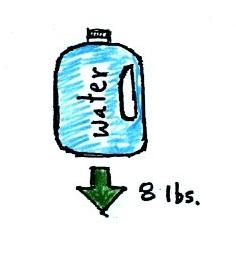Fri., Feb. 5 notes

Friday Feb. 5, 2016

Selections from Lucius featured before class today: "Until We Get There" (4:59), "Turn It Around" (4:10), and "How Loud Your Heart Gets" (6:58) and "Two of Us on the Run" (4:51).

The Practice Quiz has been graded. This semester's results is low but, as the chart below shows, is pretty typical. The 68% average for the 11 am class is well above average.

Semester	11 am MWF class	1 pm MWF class
S16	68%	61%

Semester	8 am T Th class	9:30 am T Th class
F15	61%	61%
S15	61%	61%

The 1S1P El Nino reports have also been graded and were returned today.

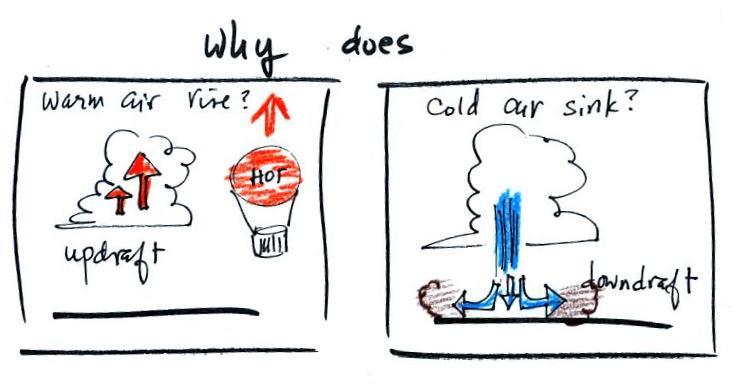
Back to trying to understand why warm air rises & cold air sinks


Hot air balloons floating over the Rio Grande river during the Albuquerque Balloon Fiesta (source of the photo)	Photograph of a microburst, a localized intense thunderstorm downdraft, that hit Wittmann Arizona in July 2015. Surface winds of 55 MPH were measured. (source of the photo)

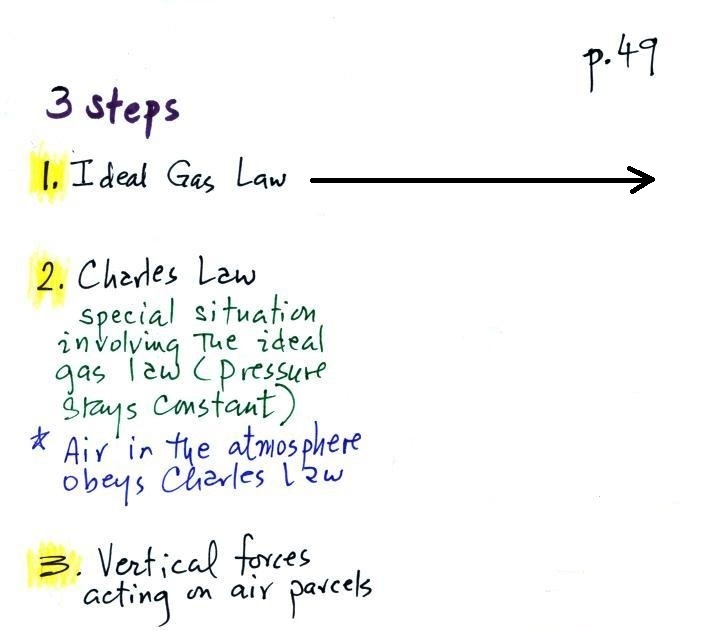
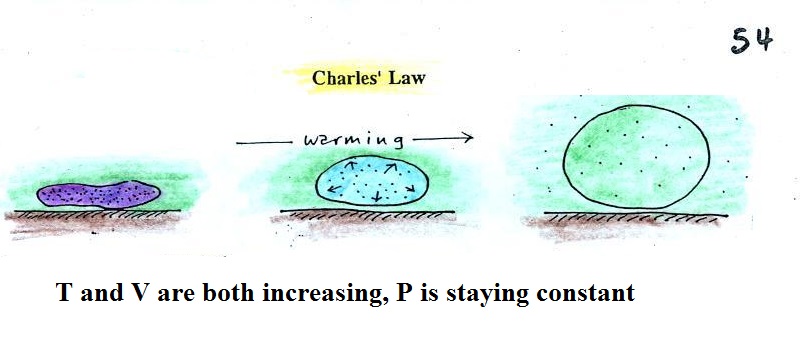
Step #2 Charles Law

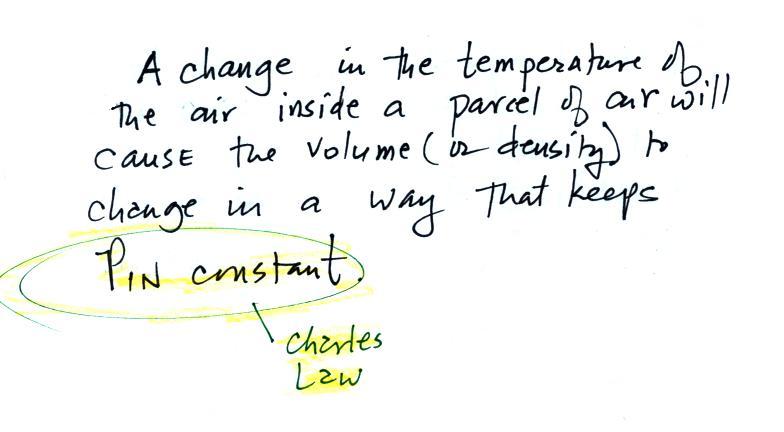
Charles Law means that P (pressure) in the ideal gas law stays constant. Changing the temperature of a volume of air will cause a change in density and volume; pressure will stay constant. This is an important situation because this is how volumes of air in the atmosphere behave.

This is probably the most difficult part of today's class and is worked out in lots of detail.

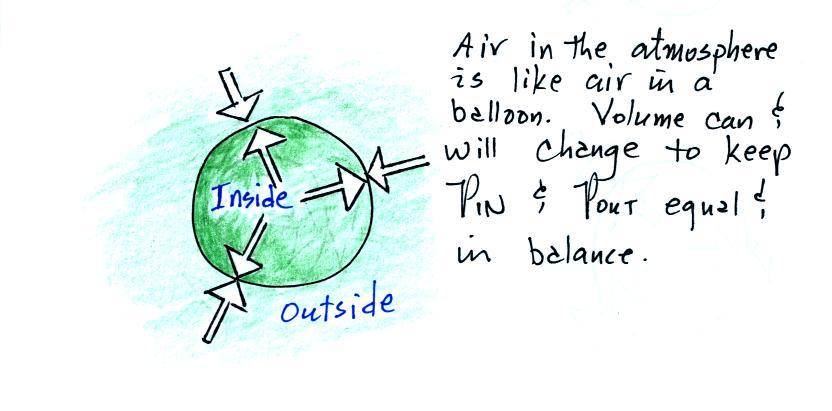
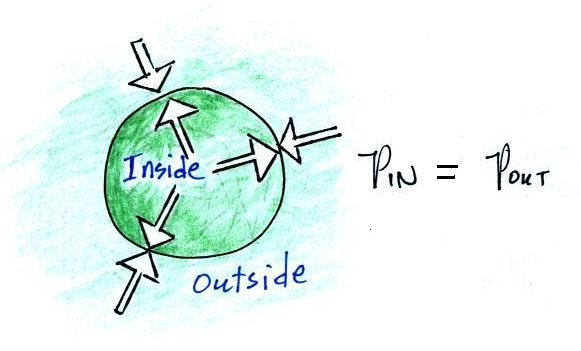
We will use a balloon of air. The air inside and outside the balloon (or parcel) are exactly the same.

The pressure of the air surrounding the balloon pushing inward is balanced by the pressure of the air inside the balloon that is pushing outward. If we change something inside the balloon that upsets this balance, the balloon would expand or shrink until the pressures are again in balance.

Volumes of air in the atmosphere will behave the same way.

First let's imagine warming the air inside a balloon. We'll won't change the temperature of the air outside the balloon.

Increasing the temperature will momentarily increase the pressure. This creates an imbalance. Now that P inside is greater than P outside the balloon will expand.

Increasing the volume causes the pressure to start to decrease. The balloon will keep expanding until P inside is back in balance with P outside.

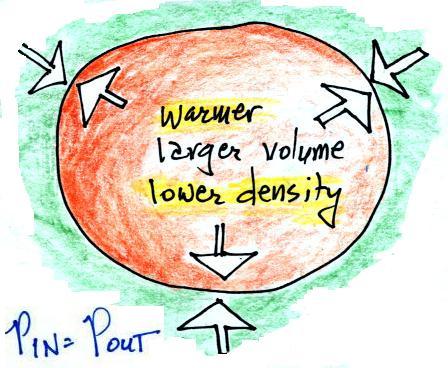
We're left with a balloon that is larger, warmer, and filled with lower density air than it was originally.

The pressures inside and outside are again the same. The pressure inside is back to what it was before we warmed the air in the balloon. You can increase the temperature and volume of a parcel together in a way that keeps pressure constant (which is what Charles' law requires). This is equivalent to increasing the temperature and decreasing the density together and keeping the pressure constant.

In nature the change in temperature and volume occur simultaneously. It's like jumping from the first to the last step above.

Warming a parcel of atmospheric air will cause the parcel volume to increase, the density of the air in the parcel to decrease, while pressure remains constant.

We can go through the same kind of reasoning and see what happens if we cool the air in a parcel. Actually you should see if you can figure it yourself. I've included all the steps below. We'll just skip to the last step in class.

We'll start with a parcel of air that has the same temperature and density as the air around it.

We'll cool the air inside the parcel. The air outside stays the same.

Reducing the air temperature causes the pressure of the air inside the balloon to momentarily decrease. Because the outside air pressure is greater than the pressure inside the balloon the parcel is compressed.

The balloon will get smaller and smaller (and the pressure inside will get bigger and bigger) until the pressures inside and outside the balloon are again equal. The pressure inside is back to the value it had before you cooled the air in the parcel.

The first and last steps, without all the intermediate and momentary details, are shown below.

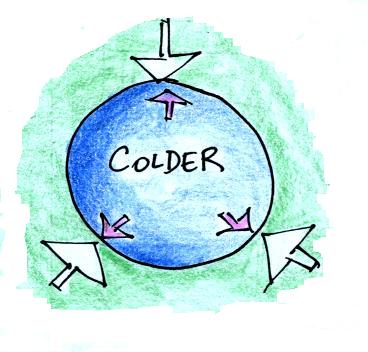
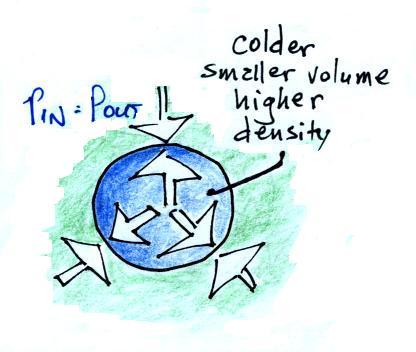
Cooling some air will cause volume to decrease and density to increase while pressure stays constant.

If you want to skip all the details and just remember one thing, here's what I'd recommend

Demonstration of Charles Law in action
Parcels of atmospheric air and air in balloons behave the same way, they both obey Charles' Law. Charles Law can be demonstrated by dipping a balloon in liquid nitrogen. You'll find an explanation on the top of p. 54 in the photocopied ClassNotes.

A balloon shrinks down to practically zero volume when dunked in the liquid nitrogen. When pulled from the liquid nitrogen the balloon is filled with very cold, very high density air.

Then the balloon starts to warm up.

The volume and temperature both increasing together in a way that kept pressure constant (pressure inside the balloon is staying equal to the air pressure outside the balloon). Eventually the balloon ends up back at room temperature (unless it pops while warming up).

All of that was just Step #2, we've still got Step #3

Step #3 Two vertical forces acting on a parcel of air in the atmosphere
(see p. 53 in the ClassNotes)

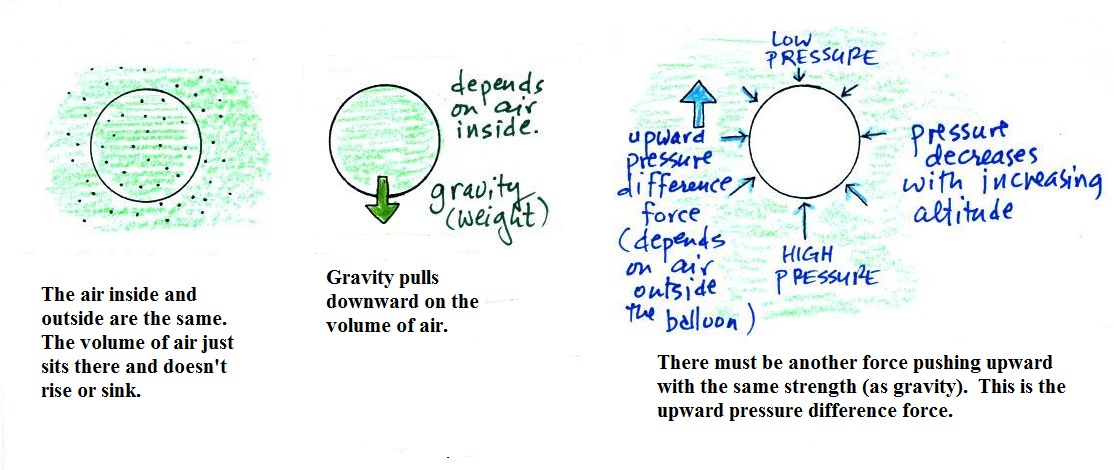
Basically it comes down to this - there are two forces acting on a parcel of air in the atmosphere. They are shown above.

The first force is gravity, it pulls downward. Most everyone knows about this force. The strength of the gravity force (the weight of the air in the parcel) depends on the mass of the air inside the parcel.

Second there is an upward pointing pressure difference force. Not too many people know about this one. This force is caused by the air outside (surrounding) the parcel. Pressure decreases with increasing altitude. The pressure of the air at the bottom of a parcel pushing upward is slightly stronger than the pressure of the air at the top of the balloon that is pushing downward. The overall effect is an upward pointing force.

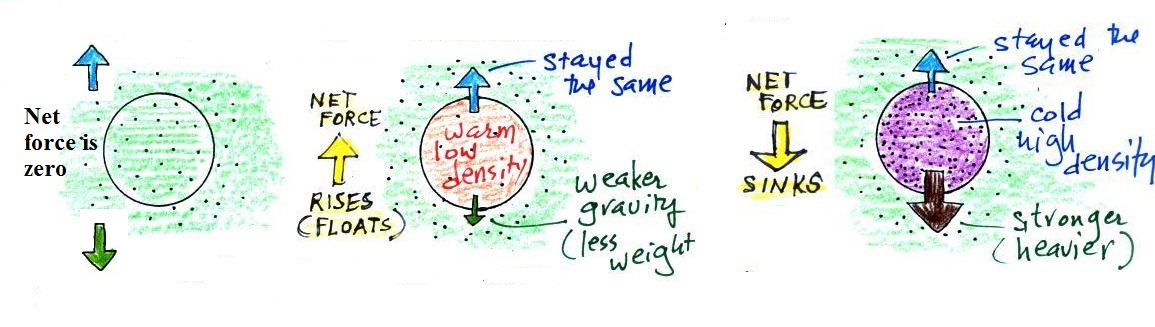
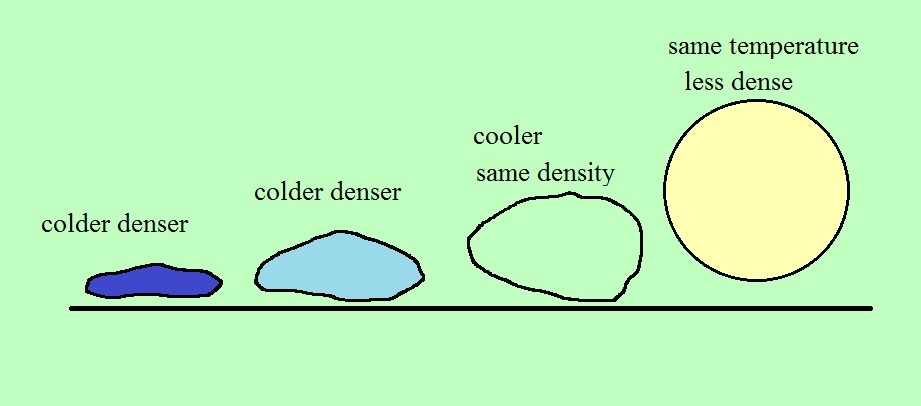
When the air inside a parcel is exactly the same as the air outside (same densities), the two forces are equal in strength and cancel out. The parcel is neutrally buoyant and it wouldn't rise or sink, it would just hover.

We'll replace the air inside the balloon with either warm low density air or cold high density air.

In the first case, a balloon with warm low density air won't weigh as much. The gravity force is weaker. The upward pressure difference force doesn't change (because it is determined by the air outside the balloon which hasn't changed) and ends up stronger than the gravity force. The balloon will rise.

Conversely if the air inside is cold high density air, it weighs more. Gravity is stronger than the upward pressure difference force and the balloon sinks.

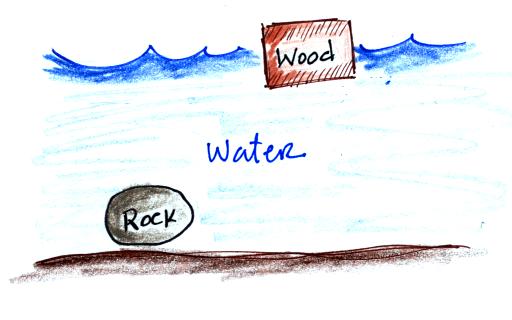
It all comes down to a question of how the density of the air in a parcel compares to the density of the air surrounding the parcel. If the parcel is filled with low density air it will rise. A parcel full of high density air will sink. That's true of things other than air. Wood floats in water because it is less dense than water.

We'll look at this in a different way after the demonstration

Here's a short demonstration of the role that density plays in determining whether a balloon will rise or sink (or hover)

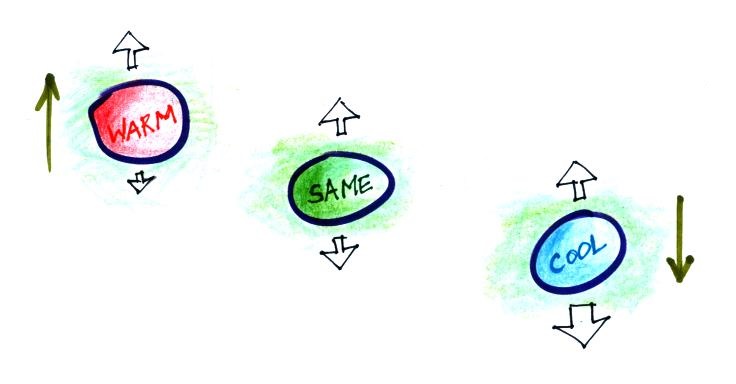
Convection demonstration

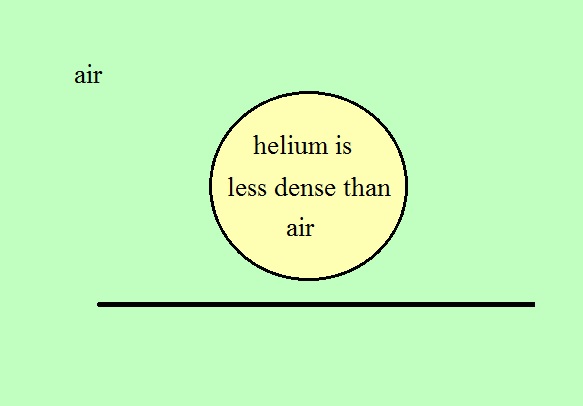
We used balloons filled with helium (see bottom of p. 54 in the photocopied Class Notes). Helium is less dense than air even when it has the same temperature as the surrounding air. The downward gravity force (weight of the helium filled balloon) is weaker than the upward pressure difference force. You don't need to warm a helium-filled balloon to make it rise.

We dunk the helium filled balloon in liquid nitrogen to cool it off. When you pull the balloon out of the liquid nitrogen it has shrunk. The helium is denser than the surrounding air. I set it on the table (dark blue above) and it just sat there.

As the balloon of helium warms and expands its density decreases (light blue). For a brief moment it has the same density as the surrounding air (green). It's neutrally buoyant at this point. Then it warms back to near room temperature where it is again less dense than the air and lifts off the table (yellow).

Free convection
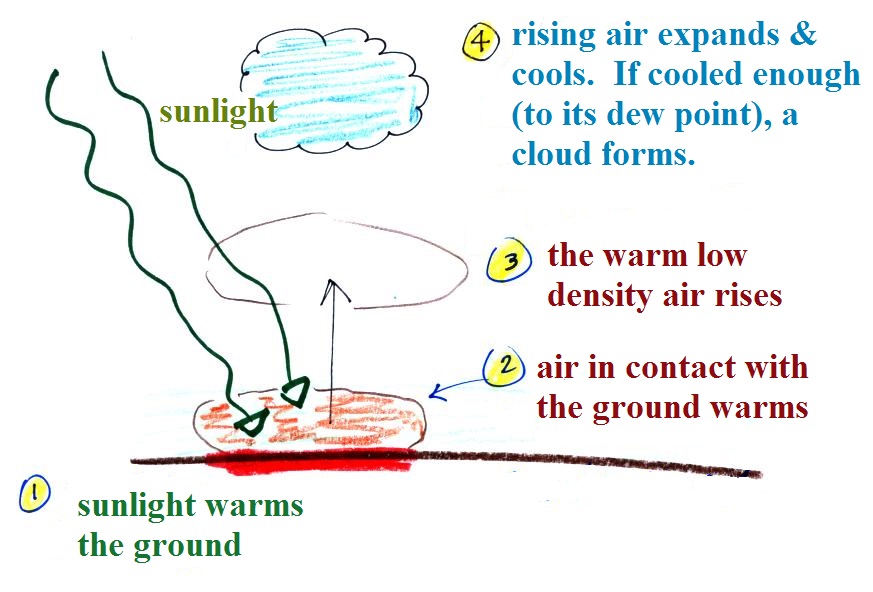
Something like this happens in the atmosphere.

Sunlight shines through the atmosphere. Once it reaches the ground at (1) it is absorbed and warms the ground. This in turns warms air in contact with the ground (2) As this air warms, its density starts to decrease (pressure is staying constant). When the density of the warm air is low enough, small "blobs" of air separate from the air layer at the ground and begin to rise, these are called "thermals." (3) Rising air expands and cools (we've haven't covered this yet and it might sound a little contradictory). If it cools enough (to the dew point) a cloud will become visible as shown at Point 4. This whole process is called convection; many of our summer thunderstorms start this way.

Archimedes' principle
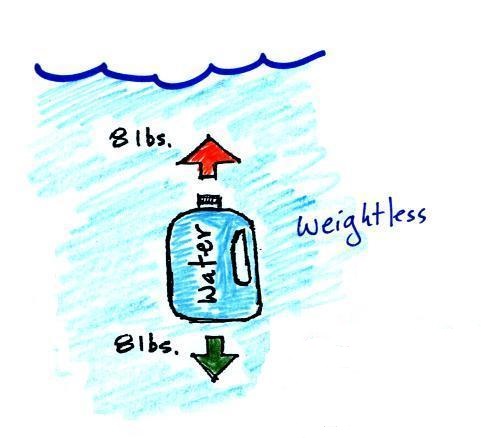
Here's another way of trying to understand why warm air rises and cold air sinks - Archimedes Law or Principle (see pps 54a & 54b in the ClassNotes). It's perhaps a simpler way of understanding the topic. A bottle of water can help you to visualize the law.

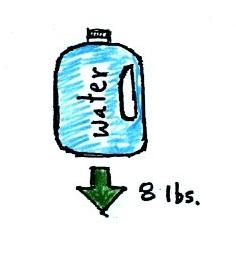
A gallon of water weighs about 8 pounds (lbs). I wouldn't want to carry that much water on a hike unless I really thought I would really need it.

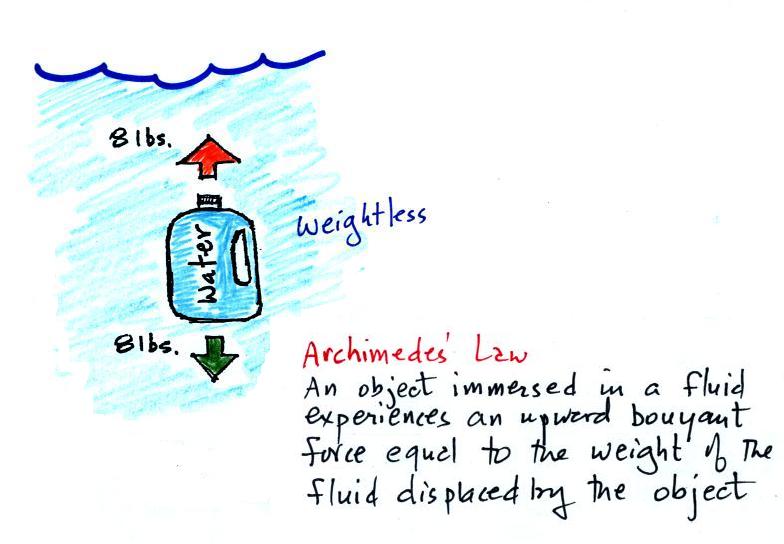
Here's something that is kind of surprising.

If you submerge the gallon of water in a swimming pool, the jug becomes, for all intents and purposes, weightless. The weight of the water (the downward gravity force) doesn't just go away. Once the jug is immersed, an upward force appears and it is strong enough to cancel out gravity. Archimedes' recognized that this would happen and was able to determine how strong the upward force would be.

In this case the 1 gallon bottle will displace 1 gallon of pool water. One gallon of pool water weighs 8 pounds. The upward buoyant force will be 8 pounds, the same as the downward force. The two forces are equal and opposite.

What Archimedes law doesn't really tell you is what causes the upward buoyant force. You should know what the force is - it's the upward pressure difference force.


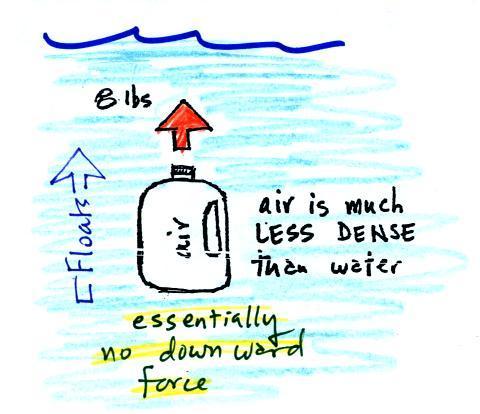
We've poured out the water and filled the 1 gallon jug with air. Air is much less dense than water; compared to water, the jug will weigh practically nothing. But it still displaces a gallon of water and experiences the 8 lb. upward buoyant force. The bottle of air would rise (actually it shoots up to the top of the pool).	The density of the material inside and outside the bottle are the same. A bottle filled with water is weightless.

Next we'll fill the bottle with something denser than water (I wish I had a gallon of mercury)


Sand is about 50% denser than water. The weight of a gallon of sand is more than a gallon of water. The downward force is greater than the upward force and the bottle of sand sinks.

You can sum all of this up by saying anything that is less dense than water will float in water, anything that is more dense than water will sink in water.

Most types of wood will float (ebony and ironwood will sink). Most rocks sink (pumice is an exception).

The fluid an object is immersed in doesn't have to be water, or a liquid for that matter. You could immerse an object in air. So we can apply Archimedes Law to parcels of atmospheric air.

Air that is less dense (warmer) than the air around it will rise. Air that is more dense (colder) than the air around it will sink.

Here's a little more information about Archimedes that I didn't mention in class.

I wanted to show one last application of some of what we have been learning - a Galileo thermometer. It's a new acquisition of mine and fairly fragile.

The left figure above comes from an interesting and informative article in Wikipedia. The right figure is a closeup view of the thermometer I brought to class.

Here's an explanation of how the thermometers work. We didn't cover this in class.
This is not something you need to worry about but I included it just in case you're curious.

The fluid in the thermometer will expand slightly if it warms. It will shrink when it cools.

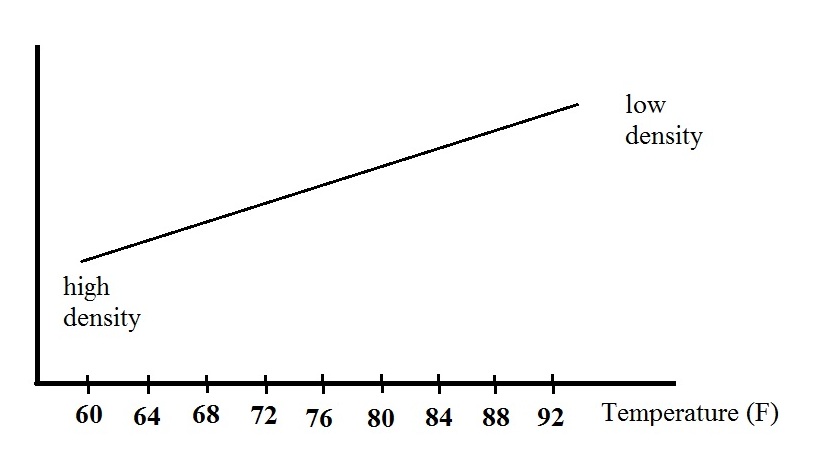
The changes in the volume of the fluid will change the fluid's density. The graph above shows how the fluid density might change depending on temperature. Note lower densities are found near the top of the graph.

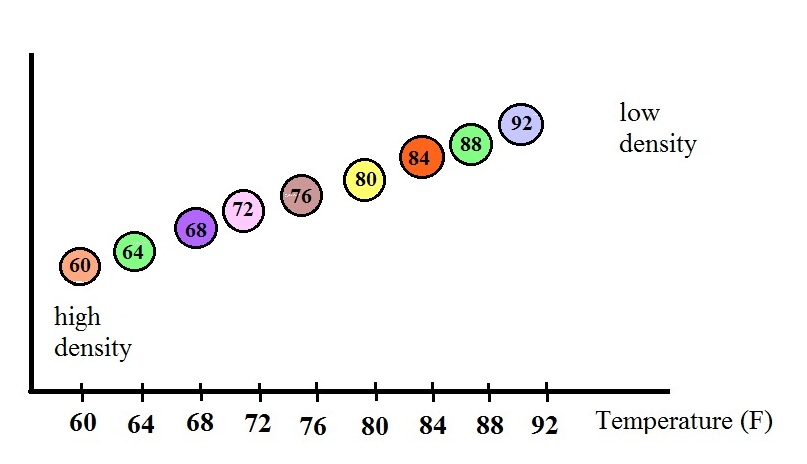
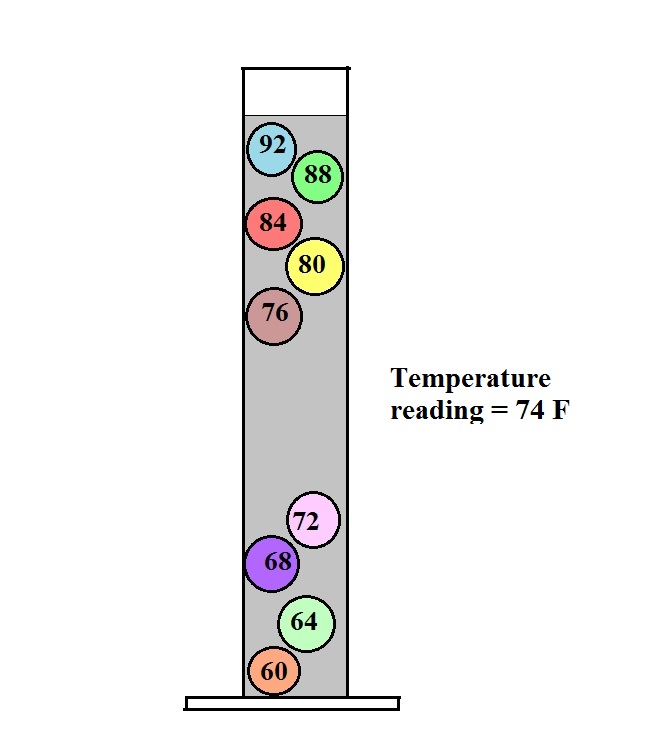
The colored balls in the thermometer all have slightly different densities. They also have little temperature tags. The 60 F ball has a density equal to the density of the fluid at 60 F. The 64 F ball has a slightly lower density, the density of the fluid when it has warmed to 64 , and so on. The densities of the floats don't change.

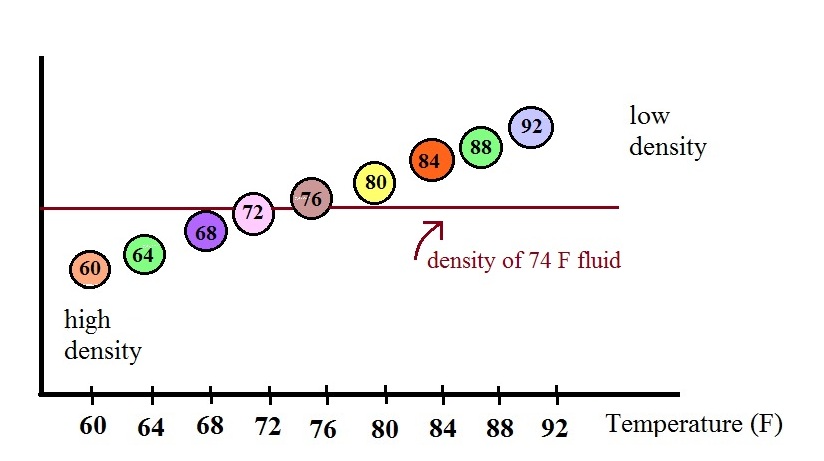
In use the density of the fluid in the thermometer will change depending on the temperature. The densities of the balls remain constant. As an example we will that the fluid in the thermometer has a temperature of 74 F. The 60, 64, 68, and 72 F balls will all have densities higher than the fluid (they lie below the 74F line in the graph above) and will sink. The remaining balls have densities lower than the fluid and will float.

The lower most floating ball in the illustration has a 76 F temperature tag. The uppermost of the balls that have sunk reads 72 F. The temperature is something between 72 F and 76 F. With this thermometer you can only determine temperature to the nearest 4 F. Also the thermometer takes quite a while (maybe an hour or two) to respond to a change in temperature.